公路隧道三台阶七步开挖法力学响应研究*

王兆亮,孙 圣,刘守花,庄 帅

(1.淮安市建筑工程质量检测中心有限公司,江苏 淮安 223004; 2.中大智能科技股份有限公司,湖南 长沙 410036; 3.淮阴工学院建筑工程学院,江苏 淮安 223003)

0 引言

目前,针对三台阶七步开挖法施工方面的研究较多,但对隧道开挖过程中受力机理的研究匮乏;调查发现,三台阶七步开挖法虽在隧道施工中应用广泛,但对施工过程中支护、围岩的力学行为认识不足,实际应用效果差异较大,主要体现在施工速度和安全控制方面。因此,为充分发挥隧道三台阶七步开挖法应用效果,确保隧道施工进度和安全,有必要开展隧道开挖过程中受力的变形研究。

本文依托某在建公路隧道工程,借助FLAC3D有限差分软件建立三维数值模型,分析隧道掘进产生的各种物理力学参数,通过对比分析数值模拟结果与实测结果,并根据数值模拟结果分析开挖过程中位移、应力和围岩塑性区规律,以期为后续隧道三台阶七步开挖法施工提供必要的理论依据。

1 工程概况

某在建公路隧道左、右两洞分离,中线点至拱顶高度10.5m,左、右拱墙宽5m。隧道洞口段地层主要为亚黏土,含水量达23.3%,孔隙比为0.698,塑性指数为17.4,该段围岩的自稳能力差。隧道采用三台阶七步开挖法掘进,参数(见图1)为:循环进尺0.75m,核心土长6m,台阶间距3m。

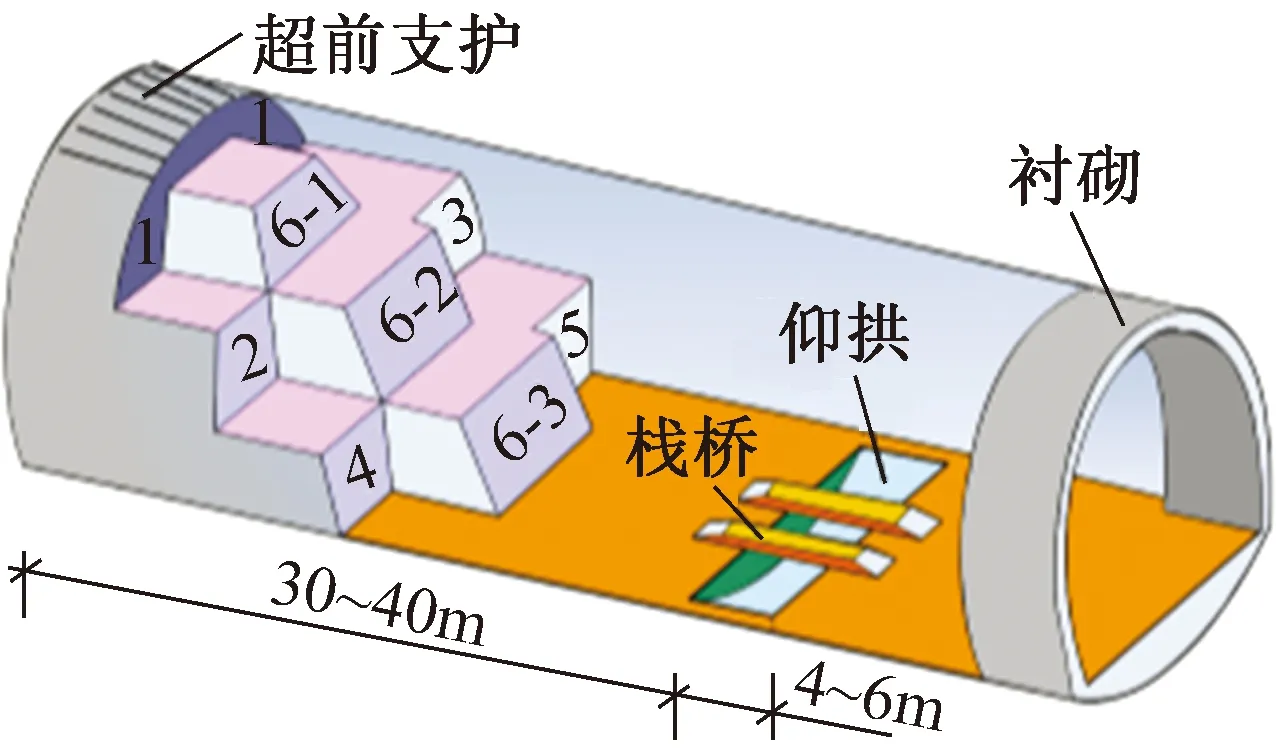
图1 三台阶七步开挖法示意

隧道采用复合式衬砌,开挖断面为12.8m(宽度)×9.2m(高度),开挖面积为110.2m2。隧道超前支护采用超前小导管加固,小导管长4m,导管外径50cm,环向间距50cm,纵向搭接1.2m。初期支护采用26cm厚C20混凝土,环向钢拱架采用I18,纵向间距75cm,纵向采用φ22钢筋连接,换线间距取80cm。二次衬砌采用45cm厚C25混凝土。

2 隧道开挖三维数值模拟

2.1 隧道开挖数值模型建立

根据现场地质条件和施工过程建立三维隧道开挖数值模型,为消除模型边界对数值模拟结果的影响,模型的横向宽度取120m(约10D,D为洞径);沿线路纵向长度为60m;竖向自隧底向下取48m。模型侧面限制水平位移,底面限制竖向位移。

岩体采用三维实体单元(zone)模拟,服从Mohr-Coulomb屈服准则,初期支护单元选择三维壳单元(shell),仰拱、二次衬砌选择三维实体单元(zone),初期支护、仰拱和二次衬砌均按弹性体考虑。该模型单元总数327 920个,结点总数 342 306 个。具体参数如表1所示,其中岩体的体积模量(K)、剪切模量(G)由式(1)和式(2)换算获得,初期支护的弹性模量按式(3)折算获得。

表1 数值模型参数

(1)

(2)

E=E0+(Sg·Eg)/Sc

(3)

式中:E为折算后的混凝土弹性模量(GPa);E0为原混凝土弹性模量(GPa),混凝土强度等级为C20;Eg为钢拱架(I18)弹性模量(GPa),Eg=210GPa;Sg为钢拱架截面面积(cm2),取30.756cm2;Sc为喷射混凝土截面面积(cm2),取1 950cm2。

将各参数代入式(3)计算可得:E=24.3×109Pa。

2.2 三台阶七步开挖法施工步模拟

具体施工流程为:①初始地应力场模拟;②拱部超前支护,开挖上弧导坑,施作初期支护;③左、右、中台阶交错施工,施作支护,且左、右保持错开3m;④左、右交错开挖下台阶边墙,施作支护并左、右保持错开3m;⑤中、下台阶预留核心土开挖;⑥仰拱断面土体开挖,二衬、仰拱每9m施作1次。循环进尺为0.75m。

3 隧道开挖数值模拟结果

根据实际施工步建立隧道开挖的FLAC3D模型,分析围岩、支护结构的物理力学状态。选取中间断面的拱顶(A点)、地表(B点)和拱腰(C点)作为主要特征点(见图2),分别对三台阶七步开挖法施工中位移、应力和围岩塑性区进行分析。

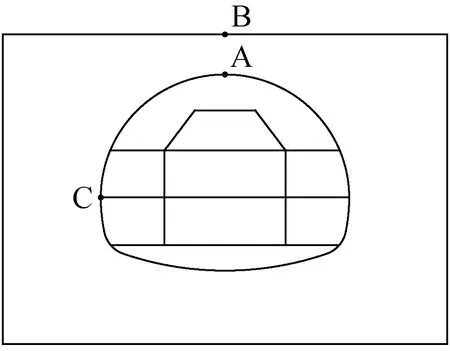
图2 特征点位置

3.1 位移分析

3.1.1整体位移分析

台阶法7个施工步均通过监测断面后的总竖向位移云图如图3所示,由云图看出,拱顶最大竖向位移10.5cm,隧道底部隆起约10.1cm。地表沉降在水平方向上的作用跨度约为3.5倍洞径,在路线前进方向超前于上导洞开挖面约1倍的开挖洞径。

图3 竖向位移云图

3.1.2数值模拟与实测结果对比分析

台阶法7个施工步开挖依次监测通过断面过程中,拱顶(A点)数值计算竖向沉降量和3个断面实测沉降量对比、拱顶(A点)纵向数值计算位移与3个断面实测位移对比及边墙(C点)计算收敛分别如图4～6所示。

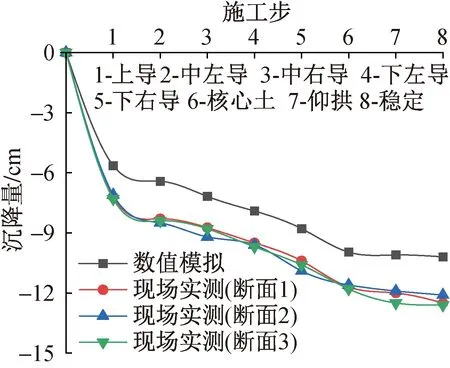
图4 拱顶沉降对比

由图4和图5看出,各施工步依次通过典型断面时数值模拟结果和现场实测结果趋势相同,平均误差为17.9%,数值模拟参数选取合理,计算结果可靠。同时看出,数值模拟结果小于现场实测结果,主要是由于数值模拟中围岩假设为均一的弹塑性体,但现场围岩复杂;且模拟设计时各施工步是依次有序衔接,即隧道开挖完成,立即运行施作初期支护,未体现现场施工的时间效应。数值模拟中拱顶稳定沉降值为10.2cm,其中上台阶开挖后拱顶沉降值为5.64cm,占总沉降的55.3%。现场实测数据中(断面1)拱顶稳定沉降值为17.6cm,其中上台阶开挖后拱顶沉降值为10.2cm,占总沉降的58.0%;拱顶纵向位移稳定值为2.65cm,其中上台阶开挖后拱顶纵向位移为1.47cm,占总位移的55.5%;其他施工步开挖造成的拱顶位移值大致相同,仰拱施作后初期支护闭合成环拱顶沉降值趋于稳定。

图5 拱顶纵向位移对比

图6显示各施工步通过典型断面时边墙的收敛过程,稳定收敛值为2.8cm,其中上导洞开挖后的收敛值为1.8cm,占稳定收敛值的64.3%;其他施工步开挖对边墙收敛影响大致相同,其中下左导、下右导、仰拱开挖施工较上左导、上右导及核心土开挖对边墙位置处收敛影响大。

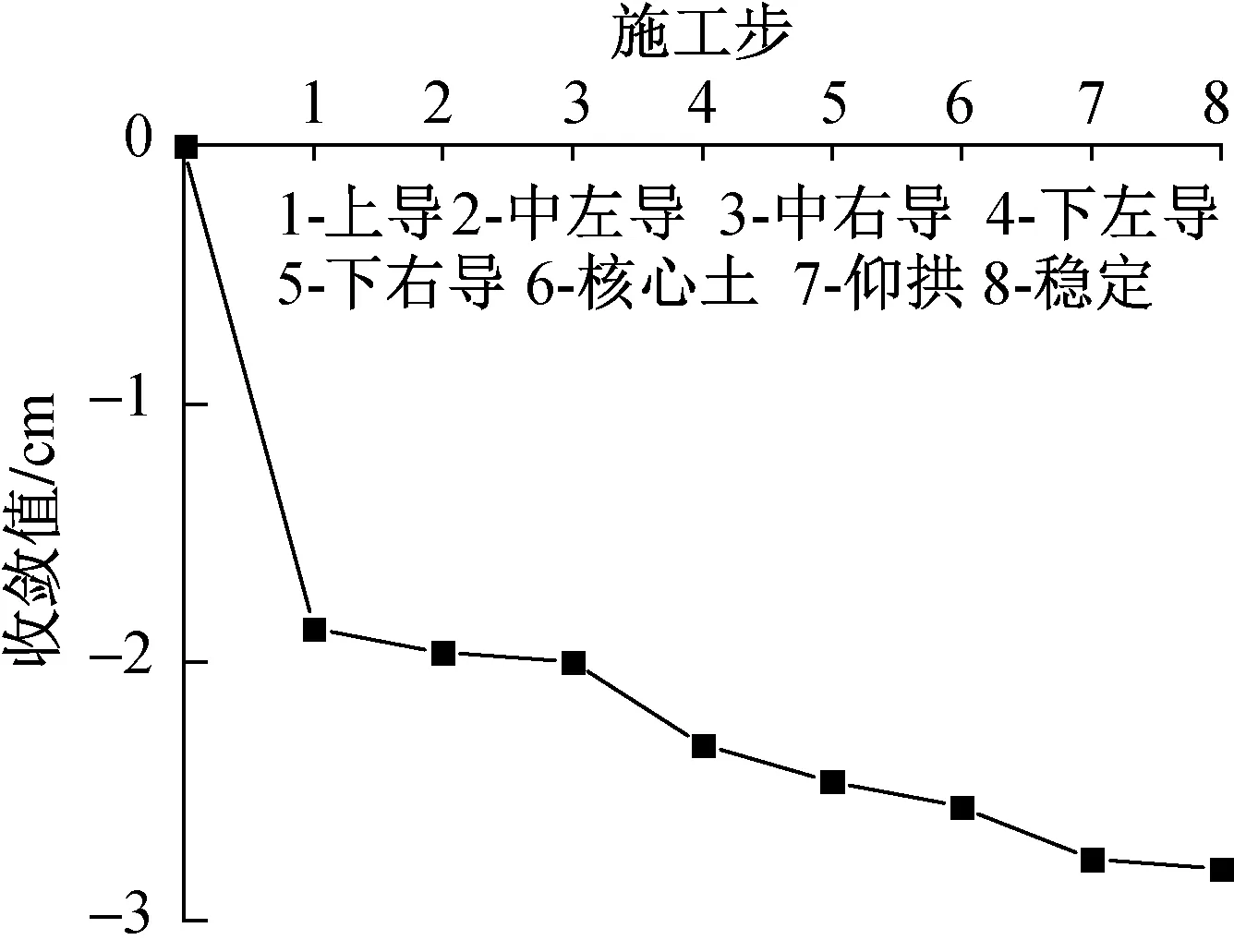
图6 边墙收敛

各工序依次通过监测断面时地表特征点(B点)沉降分析对比曲线如图7～9所示。

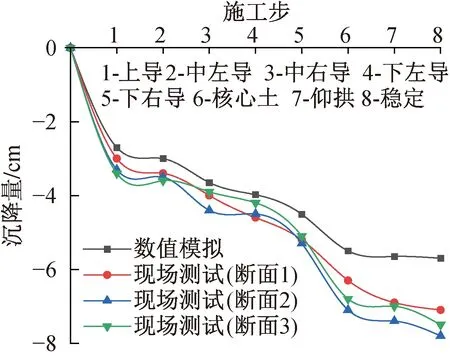
图7 地表特征点B沉降对比

图7显示,3个断面地表特征点B现场实测沉降值较数值计算值大,数值计算结果与现场实测结果的相对平均误差为13.5%。各施工步依次通过典型断面直至稳定后地表总沉降为5.7cm,上导洞开挖后地表沉降为3cm,占总沉降的52.6%,其他各施工步开挖对地表特征点沉降的影响大致相同。

图8所示数值模拟结果显示,地表沉降槽显示基本上对称,左、右交替施工对中心线的偏离影响不明显,掌子面推进才是地表沉降的主要影响因素。由图9所示数值模拟结果看出,与掌子面距离越远地表沉降越小,上导洞开挖对地表沿纵向沉降影响最大。所以,控制上导洞开挖时掌子面的稳定性是三台阶七步开挖法施工的关键。

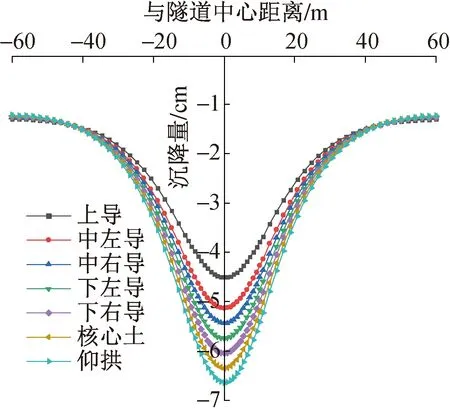
图8 地表水平沉降曲线

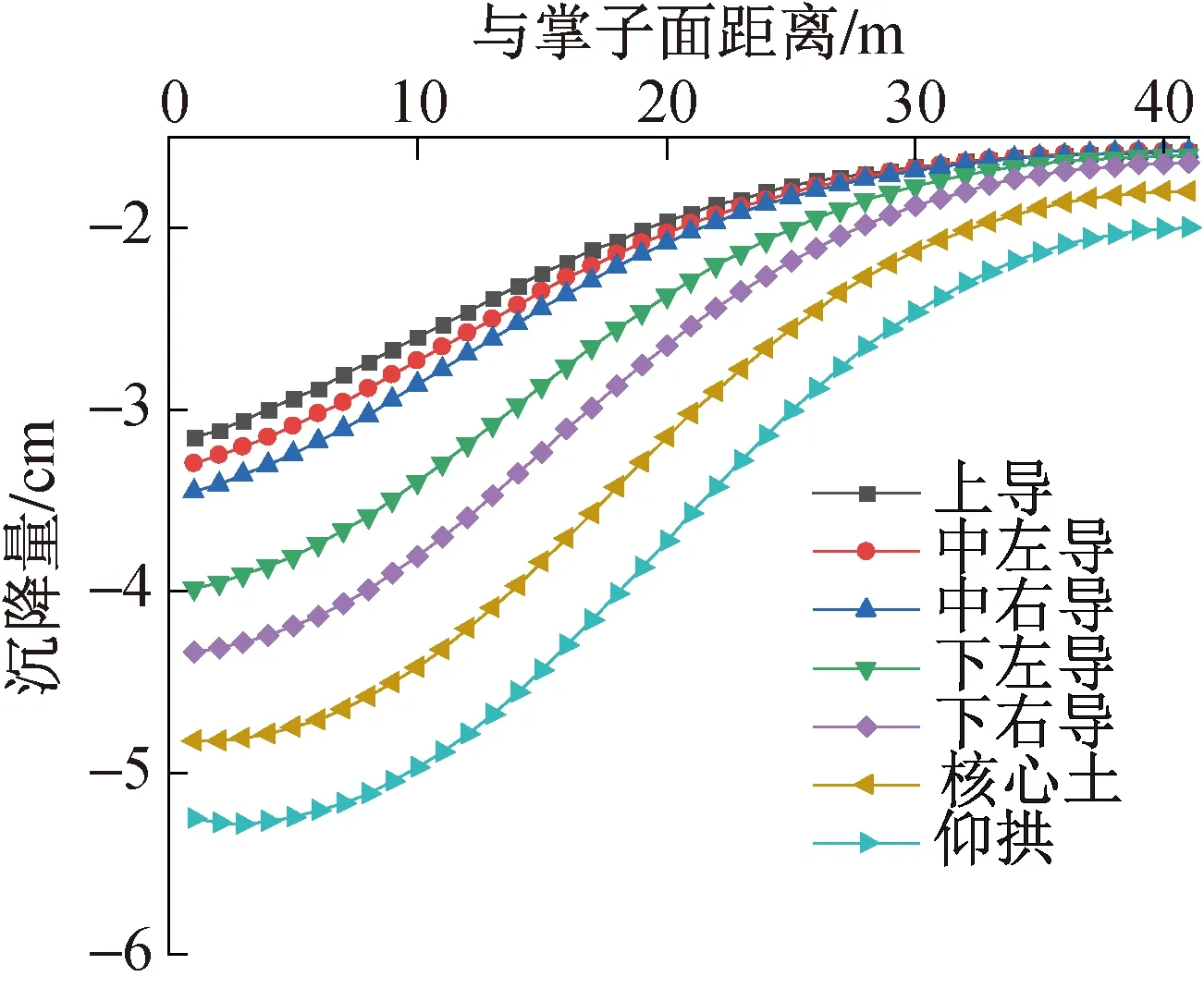
图9 地表纵向沉降曲线

3.2 应力分析

围岩的大、小主应力云图如图10,11所示,体现的是隧道的应力状态。由图看出,最大和最小主应力呈左右对称分布,围岩应力场分布随断面各施工步开挖而变化。初始应力场因隧道开挖而发生改变,应力重分布,同初始状态相比,在拱顶一定区域内的围岩应力状态改变,形成低应力区;在隧道两侧边墙的中部及仰拱区域的围岩,最大主应力在应力变化中向逐渐增大的方向发展,随着开挖的进行,应力逐渐往某一区域增大扩展,最终在拱腰位置处显现(即开挖跨度最大处)。

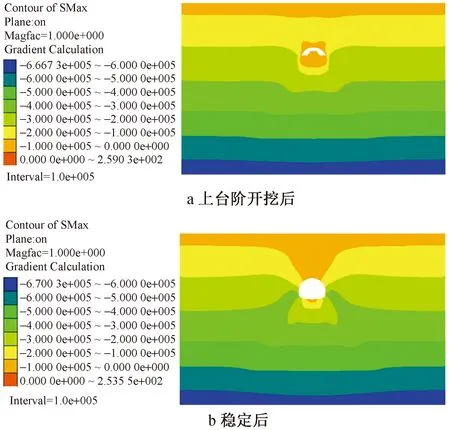
图10 最大主应力云图

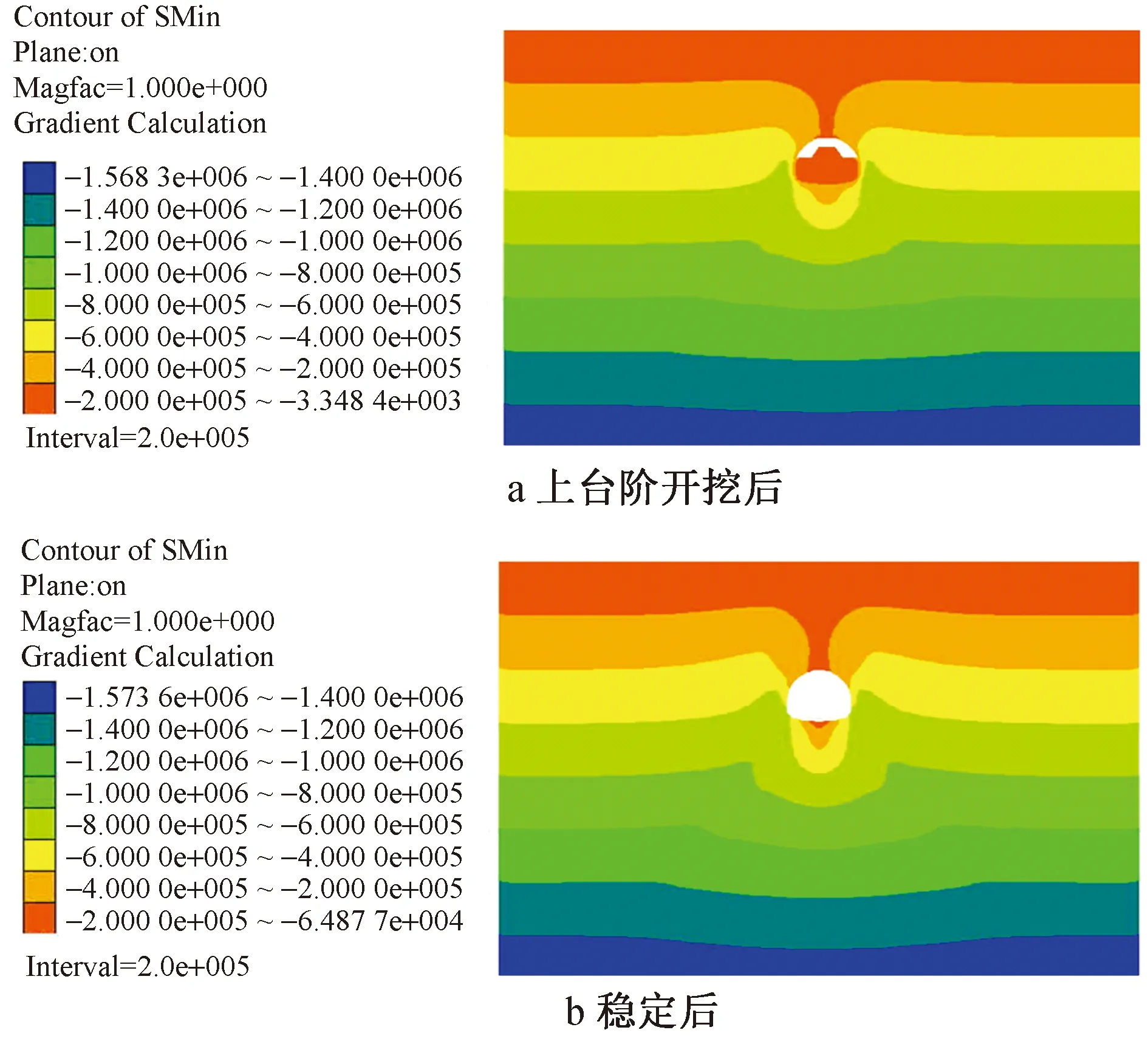
图11 最小主应力云图

3.3 围岩塑性区分析

1个施工循环完成时隧道周边围岩塑性区分布如图12所示,由图看出,隧道周边围岩塑性区在隧道施工时贯通,影响范围沿横向约0.4D,隧道前方土体在开挖方向上的塑性区,超前上导洞掌子面的距离在约0.5D,地表塑性区在开挖方向与上导洞前进距离体现较好的一致性;横断面塑性区随开挖推进分布区域不同,拱脚位置变化尤为明显,在隧道前进方向,塑性区超前上导洞掌子面的距离在0.5D,不同点在于横断面塑性区主要受上导洞推进的影响;核心土体提供的侧向力对掌子面的稳定性起积极作用,所以该区域内掌子面未出现塑性区。

4 结语

1)拱顶位置和地表沉降的数值模拟结果与现场实测结果平均误差分别为17.9%,13.5%,说明数值模拟参数选取合理,计算结果可靠。

2)数值计算结果和实测结果表明,上台阶开挖诱发的变形超过隧道总体变形的50%,该施工步是三台阶七步开挖法中控制围岩稳定性的关键环节,而初期支护及时地形成闭环对控制总体变形有较好效果。因此,上台阶开挖是隧道开挖中确保围岩稳定和限制围岩变形的关键一环,施工时应加强该工序的动态过程控制。

3)围岩应力因隧道开挖而重新分布,拱顶附近围岩形成较大范围的低应力区,而拱腰处围岩出现应力集中现象,支护设计时应适当提高拱腰部位衬砌强度。

4)隧道前方土体的纵向塑性区超前上导洞掌子面约为0.5D,后续在亚黏土地层中进行三台阶七步法开挖时,超前支护沿纵向应≥0.5D;地表塑性区纵向与上导洞推进里程基本一致;核心土体对应掌子面未出现塑性区,核心土有利于掌子面稳定。