无参考值情况下自诊断传感器设计方法研究

蒋栋年,高玉鑫

(兰州理工大学电气工程与信息工程学院,甘肃兰州 730050;兰州理工大学甘肃省工业过程先进控制重点实验室,甘肃兰州 730050)

1 引言

随着现代工程系统集成度、复杂度和智能化的快速提升,所配置的传感器越来越多,故障风险亦随之提高,若传感器故障数据于闭环系统中传播,将带来难以估量的影响及损失.传统的定期健康评估方式费时费力,因此,人们对传感器测量系统的自诊断能力提出了更为迫切的需求.

自诊断传感器通常具备故障检测与分离的能力,并可在一定程度的故障下对传感器实现数据恢复[1–2].自诊断传感器可追溯至1993年提出的自确认传感器技术[3],牛津大学控制工程研究所相继研究出自确认溶解氧传感器、自确认数字科里奥利流量计、自确认涡轮流量计[4–6]等.文献[7]提出了一种自动驾驶系统中汽车感知传感器的故障检测和恢复方法,以使系统可以测试、隔离故障并恢复故障数据.此外,一些学者也对用于步态分析的传感器展开了自测试与自校准方法的研究[8–9].

研究表明,对于无参考值的传感器测量系统,提升传感器冗余度是使系统具备传感器自诊断能力的主要途径之一[10].目前自诊断传感器设计方法主要包括硬件冗余法、解析冗余法和基于知识的方法[11–12].自诊断系统需考虑故障自诊断模块的设计,以使其具备及时判断诊断对象并保存故障信息的能力.目前传感器的自诊断大多采取系统与算法相结合的途径[13].文献[14]通过多传感器融合预测输出的方式,提出了一种传感器自检测和自诊断方法,同时利用机器学习等算法处理了传感器运行过程中的突发故障状态.然而,目前的研究方法仍需为自诊断传感器设定参考值作为故障检测标准,限制了自诊断传感器的应用范围.在对设备本体进行可靠性评估与测试时,故障事件的定义及观测易于实现,而对传感器感知信息进行准确性评估时,由于其自身为其余设备的参考信息,则需再设立一个准确的参考值,判断传感器测量数据是否偏离正常范围.在非平稳工况、环境测量等场景下,传感器参考信息的获取费时费力,乃至无法获取,这也制约了自诊断传感器从理论走向实践.

单一传感器实现故障自诊断较为困难[15],传统上,传感器信息可靠性可由测量精度的概率分布来表示[16–17],通过分析故障检出率以及漏报率、误报率对传感器进行故障建模.然而,测量系统中各传感器的信息是相互关联的,若能挖掘其中冗余关系,将为传感器故障的自诊断和数据恢复提供新途径.文献[18]借助Gaussian Copula进行传感器误差建模,借助冗余关系模型实现无参考情况下的传感器故障检测.冗余的存在为自诊断传感器的参考数据提供依据,有助于建立更为准确的似然函数,并借助贝叶斯理论解决传感器的自诊断问题.文献[19]利用贝叶斯推理求出基于先验概率的条件概率密度函数的对数似然函数,来根据不同的优化目标推导出传感器所选择的目标函数.

鉴于此,本文在无参考情况下提出了一种自诊断传感器信息可靠性的实现方法,借助统计方法对传感器进行故障建模,结合多个传感器间存在的冗余关系,通过在有参考的情况下证明了模型的准确性,建立无参考值时传感器测量值的似然函数,利用贝叶斯理论给出传感器的故障概率,进而使得系统传感器具备自诊断能力.本文主要贡献包括: 基于传感器测量数据,考虑不同传感器之间的冗余度,给出了以冗余度为约束的传感器故障统计模型;利用传递熵对传感器测量数据进行评价,量化了传感器之间数据传递的因果关系;基于建立的故障统计模型,通过构建似然函数,引入易于获取的数据统一性观测值,利用贝叶斯推理和故障定位算法给出了无参考值的传感器故障自诊断判定方法.

2 传感器故障的分析与建模

2.1 传感器故障的统计模型

考虑具有n个冗余传感器的测量系统,这里的冗余表示为传感器测量的物理量相同,如温度、压力、物体识别等,也可以理解为不同用途传感器测量值之间存在相互影响的因果关系.

假定这n个传感器均具备正常运行的参考值,通过测量残差信息便可获取某一传感器i ∈(1,2,···,n)的故障状态.设传感器测量数据采样间隔为T.为了便于分析,认为当传感器测量状态xi=1时,第i个传感器运行正常,反之,xi=0时故障发生.本文不对故障类别进行区分,亦未区分故障造成的数据增减.根据上述分析,可将传感器测量数据视为二值随机变量Xi,即为n个传感器中故障个数之和,则传感器出现故障的概率为

其中:k为发生故障的传感器数目;pm为每个测量周期中传感器发生故障的概率.

由于测量数据之间的冗余关系,使得它们应为统计相关,即Pr(Xi=0)并非独立分布.在测量系统中,传感器测量数据的异常样本数在统计学中可认为服从二项分布[20].而在测量数据之间存在统计相关性时,则不能单独使用二项分布分析统计规律,否则将因离散度较高而导致过大的建模误差[21].文献[22]中提出β–二项分布的统计建模方法,既考虑了不同传感器故障时的统计独立性,也涉及了不同传感器样本之间的统计相关性,使得对传感器测量数据的观测更加合理.鉴于此,在第m个采样间隔内,有km个传感器故障时,运用β–二项分布模型对传感器故障概率进行统计建模,其满足[23]

其中:α和β为β分布的参数;n为传感器总数;km为测量系统中故障传感器的个数;为Gamma函数;m表示采样间隔,当不考虑采样间隔影响时,可以直接将数据视为传感器测量数据.

上式中α和β不同时,会直接影响β–二项分布的分布特性,其取值与传感器的故障概率和传感器统计数据的相关性密切相关,可将这两个参数取值为

其中:pav为某一测量间隔内的传感器平均故障概率,λ为传感器测量数据的冗余度.可以看出,对于以β–二项分布构建的传感器故障模型,冗余度是模型准确性的关键,因为模型参数由冗余度决定.

2.2 传感器测量数据的冗余度量化评价

通常来讲,冗余就是对系统功能的重复配置,传感器冗余一般包括硬件冗余和解析冗余,这里评价的是传感器之间的解析冗余度.对于由多个传感器组成的测量系统,若传感器之间存在解析冗余关系,则其测量信息之间的共有信息,称为互信息.互信息越大,即两变量间冗余度越大.然而互信息估计受联合概率密度估计的限制,其准确度会影响变量冗余度,且无法表示传感器之间信息传递的方向,因此在互信息的基础上引入传递熵,其定义如下:

其中h为传感器数据预报范围,通过调节h可使传递熵适应变量间的不同延迟.

为表征传感器之间的因果关系,可以利用两个传递熵的差值,即

其中:λsi→sj为数据之间的冗余度.借助传递熵方法即可构建传感器间信息传递的冗余关系模型.令λsi→sj>0表示传感器si向sj信息熵的影响更大,si是导致sj变化的原因.相反的,令λsi→sj<0表示sj是si变化的主要原因.若λsi→sj接近于0,则表示两个变量无明确因果关系.

3 有参考值时的自诊断传感器设计

3.1 传感器平均故障后验概率

将传感器测量数据分为M个采样间隔,任意一个采样间隔m ∈{1,2,···,M}.若传感器测量数据是独立分布的,且故障不具有间歇特性时,在M个采样间隔内任意取一段数据均可得到近似传感器故障概率.然而传感器之间存在的冗余关系,必然存在互相影响的因果关系,且当故障具有间歇特性时,不同采样间隔内的数据是具有相关性的,将导致传感器的故障概率可能被低估,尤其是当采样间隔取的越小时,低估的可能性越大.考虑到这一因素,这里选取的采样间隔m大于100个测量值,并且使其满足采样间隔数目M>5.则传感器故障概率密度函数为

其中k={k1,k2,···,kM}为不同采样间隔下传感器故障数目的集合.对式(7)进一步推证可得

其中:f(pav,λ)为传感器故障的先验概率密度函数,在无法获取更多传感器的信息时,对于这种未知的先验概率,可以利用最大熵原理来获取[24];f(k|λ)和f(λ)分别为冗余度条件下传感器故障数目分布和冗余度分布,设定其为常数;L(pav,λ)为似然函数,满足

似然函数L(pav,λ)可借助式(2)来获取.在有参考值情况下,可利用似然函数不断修正传感器故障先验概率,通过获取后验概率来确定故障平均概率.由于P(K=km|pav,λ)是由β–二项分布的特性决定的,当传感器之间冗余度较高时,可以明显提升传感器的故障可诊断性能.

3.2 故障检测和定位

若测量系统中某一传感器发生故障,则可能导致整个测量系统处于不健康运行状态,以此为判定依据,评估测量系统中是否有传感器发生故障,如下式所示:

其中γ为测量系统中故障检测的阈值.当满足式(10)时认为传感器测量系统至少有一个传感器发生故障.通过下式可得到测量系统中传感器故障的概率:

由于上式是非线性积分问题,计算较为困难,因此Pr(pav|k,λ)考虑采用马尔科夫链蒙特卡洛(Markov chain Monte Carlo,MCMC)方法进行数值近似.

对于传感器测量系统,可能存在多个传感器发生故障,因此无法依据传统故障定位方法直接进行定位,考虑引入故障贡献度Fc实现故障传感器准确定位

其中:f(pav,λ)为传感器平均故障先验概率密度函数;f(pav|k,λ)为传感器平均故障后验概率密度函数.提出的故障定位算法具体如表1–2所示.

表2 算法2: MCMC抽样算法Table 2 Algorithm 2: MCMC sampling algorithm

4 无参考值时的自诊断传感器设计

4.1 设计原理

对于无参考值测量系统,缺乏测量过程数据准确性的判断依据,仅考虑单一传感器难使其具备自诊断能力.若系统中多个传感器形成冗余,可参考冗余传感器测量数据对其运行状态进行评估.在满足冗余度评价指标要求的传感器集合范围内,欲评估传感器是否故障,需分析传感器数据变化是否满足正相关.若在一个测量间隔内,某传感器测量数据变化异常,而其余传感器未随之发生明显变化,可初步认为该传感器发生故障,此处不考虑除该传感器外其余传感器均故障的极端情况.

考虑到没有参考值作为判断传感器输出正确性的依据,令观测值y作为传感器输出的分类指标,表示传感器数据的差异数量,km表示传感器测量系统在第m个测量间隔内故障传感器个数.以3个传感器组成的测量系统为例,当所有传感器均运行正常或同时故障,即其数据表现是类似的,难以进行有效区分,满足y=0.对于其他情况,均有1个传感器数据和其余两个表现不同,满足y=1,如图1所示.

基于以上原理,欲使传感器具备自诊断能力,需解决两个关键问题:一是根据传感器测量输出的分类指标y确定异常个数;二是判断具体的故障传感器.

4.2 自诊断传感器设计过程

借助传感器平均故障概率pav来判断传感器是否发生故障,在M个测量间隔中,分类指标y={y1,y2,···,yM},根据贝叶斯定理可得

其中:f(pav,λ)为传感器故障的先验概率密度函数;f(pav|y,λ)为已知冗余度量化评价指标λ约束下的传感器故障后验概率密度函数;L(pav,λ)为似然函数,满足

由于当前情况下缺少传感器参考数据,为考虑每一种传感器发生故障的分类指标y,将上式改写为

其中max(y)为传感器数据分类指标的最大值,满足max(y)=[(n+1)/2].当y符合某种特定分类指标时,似然函数会为后验概率的估计提供支撑.由此可得,测量系统出现传感器故障需满足下式:

有参考值和无参考值情况下,单个传感器发生故障并无本质区别,因此γ和有参考时的阈值大小相同.与式(11)类似,测量系统中传感器故障概率为

由于式(11)和式(17)为非线性积分运算,对于β–二项分布的复杂结构进行解析求解面临很大困难,因此考虑采用MCMC方法进行数值近似[25].

对于传感器测量系统而言,当后验概率密度函数超出阈值时,至少有一个传感器发生故障,而在无参考值情况下,通过输出分类指标ym仅能确定测量系统中传感器输出相同的类别,无法确定故障传感器个数.在实际工业现场,测量系统很少出现有一半以上传感器同时故障,因此可假定ym<(n+1)/2,由此可通过表3中算法对故障传感器个数进行确定.

表3 算法3: 故障传感器个数确定Table 3 Algorithm 3: The number of faulty sensors is confirmed

此外,还需对故障传感器进行准确定位.不难发现,在已知故障传感器个数的情况下,无参考值和有参考值并无差别,因此可同样通过引入故障贡献度,再利用故障定位算法1对故障传感器进行定位.

5 仿真实验分析

5.1 仿真案例: 镍闪速炉系统

使用闪速炉系统对镍进行精矿熔炼时,需从矿物中快速提取所需金属材料,镍闪速炉熔炼装置如图2所示.

图2 闪速炉部件图Fig.2 Component drawing of flash furnace

闪速炉炉体布置有大量温度传感器以控制镍熔炼的氧化反应过程,如图3所示.

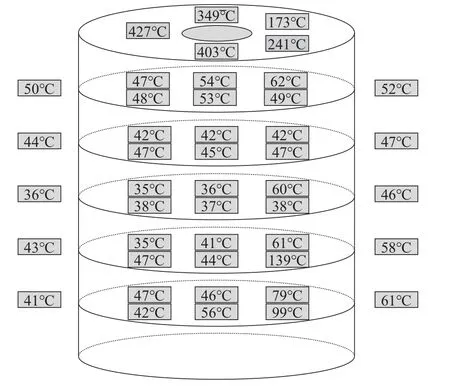
图3 闪速炉炉体温度传感器布局Fig.3 Layout of temperature sensor of flash furnace body

5.2 闪速炉温度传感器常见故障分析

温度传感器为闪速炉检测反应过程的核心装置,受工业现场高温、高压、粉尘等因素影响,极易发生故障.从测量数据角度出发考虑其常见故障类型,根据现场采集数据,整理如表4所示.本文主要研究温度传感器出现高噪声故障的情况.

表4 温度传感器常见故障描述Table 4 Common fault description of temperature sensor

5.3 镍闪速炉传感器冗余量化评价

对测量数据进行冗余度量化评价,所得传感器间传递熵量化评价指标如图4所示.为了方便说明,图4仅选取测量系统中10个传感器进行冗余度评价.

图4 测量系统中传感器间的传递熵Fig.4 Measuring the transfer entropy between sensors in the system

从图中可以看出传感器本身的传递熵为1,图中λs0→s1=0.23而λs1→s0=0.54,说明传感器s1对s0影响大于s0对s1的影响.图4展示了传感器之间的因果关系,为实现传感器的自诊断提供了依据.

5.4 有参考值时的自诊断传感器设计

5.4.1 故障检测

有参考值情况下,测量周期内传感器故障数目km已知,应用贝叶斯定理即可得到传感器故障的后验概率密度函数.

测量系统中温度传感器任务、环境均相同,且相对位置固定,为方便检测,可选取炉体同一区域内的10个传感器,即n=10.在有参考值情况下,尽管确定了测量系统中km个传感器异常,受不确定因素影响,测量系统可能出现误报、漏报.那么,若连续M次测量之后后验概率密度函数f(pav|k,λ)超过阈值γ,可认为测量系统中有传感器发生故障.

对于传感器故障阈值的选取,在后验概率符合高斯分布的前提下,利用Lilliefors假设检验可获取后验概率密度函数的显著性水平,在此基础上,获取后验概率密度函数计算结果的期望和方差[26]为

其中Tf为在单一传感器故障情况下,获取50组故障后验概率数据的序列.

设显著水平α=0.05,即置信度为95%,则相关系数Z=1.96,满足

由此可得阈值计算公式如下:

利用多次测量获取的传感器数据统计特性,并按照上述方法可求取传感器故障阈值为0.56.

选取连续10个测量周期,可得传感器故障后验概率密度函数均超过阈值0.56,且在后续测量周期中,后验概率密度函数保持不变,可知测温系统中至少一个传感器发生故障,如图5所示.

图5 有参考值的后验概率密度函数Fig.5 A posteriori probability density function with reference value

5.4.2 故障定位

当评估出测量系统中存在传感器处于不健康状态时,利用故障定位算法得到传感器故障贡献度如图6所示.

图6 有参考值时故障定位Fig.6 Fault location with reference value

明显看到,在高噪声故障情况下,14位置与20位置的传感器故障贡献度有显著增加,故障传感器有可能为14号与20号传感器.对建立的模型在多个测量周期内经过反复测试得到传感器故障贡献度的均值如表5所示.可以看出,在多个测量周期内,大部分传感器的平均故障贡献度均在0.170左右,而14号与20号传感器在0.723左右,远远高于其他传感器.

表5 传感器故障贡献度均值表Table 5 Sensor fault contribution average table

检测到故障传感器后,对故障传感器进行剔除,利用建立的模型对测量系统进行重新评估.图7为500个测量周期内后验概率密度函数的均值和方差.从图中可以看出,剔除故障传感器后,后验概率密度函数并未超过阈值,其均值稳定在0.143左右,方差稳定在3.2 e–06左右,说明其余传感器并未出现故障,14号与20号位置的传感器确为故障传感器.

图7 有参考时后验概率密度函数的均值和方差Fig.7 Mean and variance of posterior probability density function with reference

5.5 无参考值时自诊断传感器

5.5.1 模型描述

无参考值情况下,欲实现测量系统传感器自诊断较为困难,尽管可通过历史数据获得先验概率,然而无法得到测量系统传感器故障个数km,难以建立有效似然函数,通过贝叶斯理论无法得到后验概率密度函数.鉴于此,提出了传感器的输出分类指标ym如图8所示.与传感器故障个数km不同,传感器输出分类指标通过对测量系统中传感器输出表现出的不同形式进行划分,并利用分类得到不同表现形式的传感器,获取测量系统中传感器故障的后验概率密度函数,以实现传感器的自诊断.

图8 有/无参考情况下传感器故障概率Fig.8 Sensor failure probability with or without reference

图8(a)为n=10,pav=0.04时,有参考值情况下传感器误差概率,图8(b)为无参考值情况下,利用相应的统计预期观测频率Y得到的传感器故障概率.从图中可以看出,无参考值情况下,Y=0 时传感器故障概率恰好等于有参考值情况下km=0和km=5的和,即测量系统中10个传感器发生故障输出所表现的形式与无传感器故障所表现的形式相同,以此类推得到了传感器输出分类指标ym.

5.5.2 故障检测

通过引入传感器分类指标ym,利用贝叶斯推理可得无参考值情况下传感器测量系统故障的后验概率密度函数,如图9所示.在14次测量周期内,后验概率密度函数均超过阈值0.56,则测量系统中至少有1个传感器处于故障状态.由于没有参考值,无法准确判断系统中出现故障传感器的个数,因此须利用ym获取传感器故障个数.

图9 无参考情况下测量系统的后验概率密度函数Fig.9 Posterior probability density function of measurement system without reference

无参考值情况下,传感器输出分类指标ym只能通过输出形式一样的传感器来划分系统中出现故障传感器的个数,比如当ym=1时,可能是1个传感器故障或9个传感器同时发生故障,但实际工程中后者概率极小,因此会默认测量系统中只有1个传感器发生故障.通过算法3得到如图10所示的故障个数图.

图10 无参考情况下测量系统的故障个数Fig.10 Measure the number of faults of the system without reference.

不难看出,在第0,1,2个循环周期内,ym-y1≠0,说明系统中故障的个数有可能为2个、3个或者4个,因此通过重新排序,在第3,4个循环周期内ym-y1=0,则说明测量系统中故障的个数为2个.

5.5.3 故障定位

已知ym=2的情况下,利用故障定位算法得到传感器的故障贡献度如图11所示.

图11 无参考值时故障定位Fig.11 Fault location without reference value.

可以看到,21位置和30位置的传感器故障贡献度增幅明显,说明故障传感器可能为21号和30号传感器,符合ym=2的情况.为使结果更为可靠,对所建立的模型进行反复测试得到传感器故障贡献度的均值如表6所示.从表6可以看出在多个测量周期内,大部分传感器的平均故障贡献度均在0.183左右,只有21号位置和30号位置的在0.771左右,远远高于其他传感器,说明故障传感器为21和30号传感器.

表6 传感器故障贡献度均值表Table 6 Sensor fault contribution average table

为进一步验证算法的可行性,将21号和30号传感器剔除,重新对测量系统进行评估.图12为500个测量周期内,后验概率密度函数的均值和方差,从图中可以看出,当剔除故障传感器后,后验概率密度函数并未超过阈值,其均值稳定在0.305左右,方差稳定在1.4 e–05左右,说明此时系统并未出现故障,则21号和30号位置的传感器确为故障传感器.

图12 无参考时后验概率密度函数的均值和方差Fig.12 Mean and variance of posterior probability density function without reference.

6 结论

本文通过引入传感器测量数据冗余度的量化评价建立了传感器故障模型,借助贝叶斯理论进行了在无参考值情况下的传感器故障检测研究,并通过算法设计实现了对故障传感器的准确定位.虽然本文提出的方法可以在无参考值的情况下实现传感器的自诊断,但对以下两个问题还有待深入研究:

1)在利用传递熵对传感器之间的因果关系进行量化评价时,当数据量较少时会导致传递熵计算的数据发生波动.虽然波动范围有限,但对于故障模型的准确性存在一定影响,因此如何能有效改进传递熵算法进而准确的评价传感器间的因果关系是未来一个有价值的课题;

2)文中虽然实现了传感器在无参考值情况下的故障诊断,但只是考虑了系统中特定故障的情况,对于工业现场中出现的多种故障因素所设计的方案是否有效也是值得进一步深入研究的.

对于这些问题的存在,需要更深层次的考虑如何去综合传感器的自诊断能力而进行诊断设计,这是一个很有意义和值得深思的课题,同时对故障传感器进行及时的数据恢复也是笔者下一步的努力方向.