基于方位信息的无人机编队控制设计与验证

孙文涵,鲜 斌

(天津大学电气自动化与信息工程学院,天津 300072)

1 引言

近年来,无人机因其成本低、适用场景广泛、机动性强等特点,在军事与民事活动中被广泛应用[1–3].但是随着无人机所执行任务的难度不断提升,单无人机系统已无法胜任日渐复杂的飞行任务,于是国内外研究者纷纷开始了对多无人机系统协同控制的研究.与单无人机系统相比,多无人机系统在区域搜索、抢险救灾等领域有着显著的优势.但是多无人机系统中客观存在的通信时延、易受气流扰动、模型不确定性等诸多因素,为多无人机系统的控制带来了挑战[4–6].

无人机编队控制是多无人机系统研究中的核心问题.针对这一问题,国内外学者展开了深入研究,并提出了很多经典的编队控制方法[7–9],其中,Leader-Follower法的核心思路是将特定无人机设定为Leader进行自主飞行,其余无人机则通过与Leader保持一定的相对位置,从而达到形成期望队形的目的.文献[10]基于Leader-Follower 方法,对Leader与Follower分别进行轨迹规划,在考虑无人机通信时延的情况下完成了密集编队飞行试验.文献[11]提出虚拟刚体概念,将各无人机视作顶点,通过一个虚拟的刚体来定义期望队形.在这种编队方法中,队形的运动视作刚体的平移与旋转,队形的变换视作刚体形状的切换.在此基础上,该论文作者为各无人机设计了控制器使其达到期望位置,从而完成编队控制任务.为了解决上述工作中集中式编队控制方法中存在的中心节点计算量大、通信负担重、容易产生通信时延等问题,分布式编队方法成为了当前多无人机编队系统的一个重要研究方向.文献[12]将一致性方法应用于无人机时变编队的控制问题中,进行了详细的数学推导,给出了多无人机系统实现时变编队的充要条件.文中基于一致性方法设计时变编队控制策略,进行了室外实机飞行试验,验证了算法的有效性.文献[13]在虚拟刚体编队方法的基础上,考虑部分无人机无法直接获取虚拟刚体状态约束的情况,通过引入相邻无人机的跟踪状态,实现了基于虚拟刚体法的分布式编队控制.

然而,上述文献所提出的控制策略中,都基于一个默认的条件,即各机体(或系统中某几个机体)可以获得彼此之间的距离或位置信息.而在无GPS的环境下,这个条件需要无人机系统有很强的感知能力,这大大增加了多无人机编队系统的设计难度与成本.为了应对这一限制,近年来基于方位信息的编队控制受到了研究人员的关注[14–17].基于方位信息的编队控制仅需要机体获得自身与邻机的方位信息,无需机间进行通讯,也无需获取机体间的距离信息.这种控制策略对于无人机编队控制而言,具有其自身的特定优势.首先,在实际情况中,各机体可以通过无源传感器(如机载摄像头)很便捷地获取所需的方位信息[18],大大降低了对机体感知能力的要求.其次,各机体间无需进行通信,可以有效地规避多机编队问题中由于通信带来的种种问题.文献[14]将方位刚度理论推广到了任意维度,提出了多智能体编队队形可由方位约束描述的条件,极大地推动了方位信息编队控制的发展.文献[15]采用类欧拉–拉格朗日形式将方位刚性理论推广到非线性机器人系统问题的求解中,将受到非完整约束和动力学约束的单积分模型转化为类欧拉–拉格朗日模型,实现了三维非完整约束模型的方位信息编队形成与保持.数值仿真实验验证了这种算法的有效性.

文献[16]考虑了方位信息编队中的传感器约束问题,包括相机的视场限制、飞行过程中可能存在的视野遮挡等实际飞行中切实存在的情况.该论文对上述传感器约束问题进行了数学描述,并进行了实际飞行试验.实验结果表明,这种设计可以完成基于方位信息的编队保持任务.但是,上述设计没有考虑外界扰动对编队控制的影响,且无法完成编队移动任务.

对于仅依赖方位信息的编队移动问题,文献[17]研究了一类具有未知扰动的二阶模型的方位信息编队控制问题.文中通过反步法引入自适应控制设计来抵消干扰对系统的影响,并通过对偏差系统嵌入速度级期望变量,实现了方位信息编队的移动.但对于实际系统来说,完全无法获得位置信息会产生位置漂移问题.针对这一问题,文献[19]提出了方位拉普拉斯矩阵(bearing Laplacian)的概念,给出了采用锚点与方位信息约束构造独特编队队形的充要条件.在此基础上,文献[20]采取Leader-Follower式编队方式,引入Leader的位置信息为整个编队系统设定锚点,针对一阶模型和二阶模型设计了基于方位信息的目标编队跟踪控制器.上述设计通过Lyapunov方法证明了跟踪误差的收敛与编队系统的稳定性,并通过数值仿真验证了算法的有效性.文献[21]通过在Leader-Follower式方位信息编队中设置第一跟随者,实现了方位信息编队移动过程中的整体缩放,并通过数值仿真验证了算法的有效性.

在以上研究成果的基础上,本文针对多无人机系统基于方位信息的编队问题进行研究.本文主要通过反步法设计了一种Leader-Follower式的方位信息编队控制策略,解决了基于方位信息编队问题中存在的位置漂移现象,实现了多无人机系统基于方位信息的对目标编队的形成、保持与跟踪任务.本文的主要创新点列举如下: 1)目前在多数基于方位信息的编队策略中,考虑的多是较为简单的一阶、二阶模型或目标编队静止的队形保持问题.本文基于多旋翼无人机的位置动力学模型,考虑实际飞行中存在的未知扰动与风阻,设计了基于方位信息的编队控制器,实现了对移动目标编队的跟踪;2)基于Leader-Follower方法构建编队以解决基于方位信息编队问题中存在的位置漂移现象.采用反步法设计方位信息编队控制器,通过引入虚拟速度输入,将自适应控制方法与鲁棒控制方法应用到基于方位信息的编队控制问题中,并用Lyapunov方法对编队系统进行了稳定性分析;3)文献检索结果表明,当前大部分方位信息编队研究仍停留在仿真阶段;基于方位信息的无人机编队控制设计中,进行了实验验证的研究成果极少.本文自主搭建了多无人机飞行实验平台,进行了实物实验,进一步验证了所提算法的实用性与有效性.

2 问题描述

2.1 无人机运动学模型

参考文献[22–24],一个由n架无人机组成的编队系统,其中第i架无人机的动力学模型可写作如下形式:

其中:pi(t)=[pix(t)piy(t)piz(t)]T∈R3×1和vi(t)=[vix(t)viy(t)viz(t)]T∈R3×1分别表示无人机的位置和线速度;mi为无人机的质量;g为重力加速度常数.式(1)中,Ri(t)∈R3×3为t时刻无人机机体坐标系到惯性坐标系下的姿态旋转矩阵;fi(t)为无人机旋翼产生的总升力;e3=[0 0 1]T为一方向向量,Di=diag{Dix,Diy,Diz}∈R3×3为无人机阻力系数.di ∈R3×1为无人机所受未知扰动.定义辅助控制输入信号ui(t)∈R3×1为

则系统动力学模型可写为

假设1扰动项di(t)为一未知函数且有界,设其上界为,有‖di(t)‖≤.

假设2各机体无人机初始位置不重合,且在编队形成过程中不发生碰撞[17].

2.2 方位刚性图理论

无人机编队中各无人机间的连接关系可以用无向图G=(V,E)表示,其中结点集V={1,2,···,n}表示各无人机个体集合,边界集E ⊆V×V代表各无人机间的连接关系.在本文中,以(i,j)∈E表示无人机i可以测得无人机j相对于自身的方位信息gij,且无人机j为其邻机,即Ni={j ∈V:(i,j)∈E}.由无向图的连接特性可得,(i,j)∈E ⇔(j,i)∈E.其中方位信息gij定义为

其中:‖eij‖表示两机体间的Euclidean距离.gij(t)∈R3×1为一单位向量,可以通过相机或无线阵列实际测得.gij(t)∈R3×1,pi(t),pj(t)∈R3×1定义正交投影矩阵Pgij ∈R3×3如下:

其中I ∈R3×3为单位阵.正交投影矩阵Pgij ∈R3×3可以将向量投影到gij的正交补集上,即对任意与gij平行的向量x,都有Pgijx=0成立.依序将图中前nl个节点设置为Leader无人机对应的节点,其余nf=n-nl个节点设置为Follower无人机节点,将第1个Follower节点的序号记作nff,即nff=nl+1.并将图中前nl个节点归于Leader集Vl={1,···,nl},后nf个节点归于Follower集Vf={nff,···,n}.

2.3 目标编队描述

本文设计Leader-Follower结构的方位信息编队.其中Leader无人机按期望轨迹进行自主飞行,且各Leader无人机之间满足期望方位约束.然后,基于无人机动力学模型(1),对各Follower无人机设计基于方位信息的编队控制律{ui}i∈Vf,使得各无人机间的方位收敛于期望值.

目标方位编队队形p∗(t)由给定的方位约束与时变的Leader无人机位置{(t)}i∈Vt确定.与传统的基于位置的编队控制方法不同,由于缺少距离信息,在同样的Leader位置与方位约束的条件下,可能有不同的编队队形.如图1所示,当只采用方位信息对期望队形进行描述时,对于同样的期望队形,不同的Leader与方位约束条件的选择会对队形的唯一性产生不同的影响.图1(a)和1(b)的期望队形选取方式会造成队形的不唯一,当Follower沿图中箭头方向同步移动时,即使编队仍满足方位约束条件,但其队形已经发生了变化.而对同样的期望队形选择更加合理的Leader与方位约束条件,就可满足其唯一性,如图1(c)和1(d)所示.

图1 方位编队唯一性说明Fig.1 Description of bearing formation uniqueness

因此,为保证方位编队队形的唯一性,Leader与方位约束的选择需要满足一定条件.引入如下方位拉普拉斯阵[19]:

将机体按Leader到Follower的顺序进行排列,可将B划分为如下形式:

值得注意的是,采用上述方法设计期望队形,编队中Leader无人机的数量不能少于2,更为详细的理论解释可见文献[19].但即使要求编队中至少有两架机体充当Leader,Leader无人机仍占其可以组成的编队系统中很少的一部分[20].

2.4 控制目标

本文的控制目标为,对由各无人机(1)组成的多无人机系统,为各Follower无人机设计基于方位信息的控制律{ui}i∈Vf,使得各无人机间的方位与各无人机速度收敛于期望值,即各无人机间形成期望队形且以期望速度整体移动,完成多无人机系统对目标编队的形成、保持和跟踪任务.

3 控制器设计

定义无人机i与其邻机之间的势场函数为

对其沿eij方向求偏导,可得

由此定义无人机i的总势场函数为

对于式(11)编队系统采用反步法进行控制设计.选取非负函数V1(t)为

对V1(t)进行求导可得

为简化证明过程,将式(11)中的系统动力学方程改写为

其中νi=diag{vix(t),viy(t),viz(t)},Di=[DixDiyDiz]T.对于式(19)系统定义非负函数V2(t)为

对V2(t)求导,得

其中:k1,k2∈R3×1,λi ∈R3×1为正值参数;v∗(t)为可预先设定的目标编队移动速度;(t)为(t)更新律.

4 稳定性分析

定理1对于由各无人机(1)组成的多无人机编队系统.在满足假设1和假设2的条件下,通过选取合适的Leader无人机与方位约束使其期望目标编队(G,p∗(t))满足唯一性条件.对各Follower无人机设计基于方位信息的控制器(23),可使多无人机系统(G,p(t))完成对目标编队的形成、保持与跟踪任务.

证选取Lyapunov候选函数V3(t)为

对上式进行求导,并将所设计的控制律(23)代入,可得

根据Barbalat 引理[25],如果可微函数f(t),当t→∞时存在有限极限,且一致连续,那么当t →∞时,(t)→0.

即各无人机间的方位都将渐进收敛于期望值,即多无人机系统形成由Leader位置与期望方位决定的期望时变编队.证毕.

5 实验验证

5.1 实验平台介绍

为了验证本文所设计的方位编队控制算法的有效性与实用性,本文使用多无人机编队飞行平台进行了实际飞行实验.实物实验中各无人机通过自身与邻机的位置信息由式(4)获取所需方位信息,编队移动速度可预先给定.

如图2所示,编队飞行平台由4架四旋翼无人机与地面站组成,各无人机的质量分别为m1=0.923 kg,m2=0.926 kg,m3=0.905 kg,m4=0.935 kg,轴距皆为l=0.25 m.每架无人机上均搭载了ARM(advanced RISC machine)嵌入式计算板与飞行控制器.各无人机间通过Wifi进行组网,且可通过OptiTrack运动捕捉系统获取自身与其它无人机的位置信息.ARM嵌入式计算板与飞行控制器间通过串口有线连接.其中ARM嵌入式计算板以50 Hz的频率运行方位编队控制算法,并将计算所得的控制指令以MavLink信息的形式发送给飞行控制器.飞行控制器负责无人机的底层姿态控制,在接收到控制输入指令后进行解算,转化为各电机转速,最终实现来自ARM嵌入式计算板的控制输入指令.地面站用来远程登陆各机载ARM嵌入式计算板,以启动编队控制算法与实时检测各项数据情况.飞行场地长5.5 m,宽3 m,高2.5 m.

图2 实验平台Fig.2 Testbed for UAVs formation control

本文主要进行了两组飞行实验: 实验1为多无人机系统在本文所设计控制器的作用下,对目标编队的形成、保持和跟踪飞行实验;实验2为对比实验,采用文献[20]所设计的基于方位信息的编队控制器对多无人机系统进行控制,进行与实验1同样的飞行实验.

5.2 实验1: 方位编队跟踪实验

首先,选取期望队形,通过引理1设计合适的方位约束与Leader选择.由于实验场地大小的限制,各无人机飞行过程中始终保持同样的期望高度.编队期望队形的平面示意图如图3所示.

其中,1,2 号机为Leader,两Leader 间满足约束‖e12‖=1.5,g12=[1,0].其它期望方位为=[0,1],[0,1].经验算,上述设计的期望编队的方位拉普拉斯阵Bff非奇异,即上述期望编队设计满足方位编队唯一性条件,期望队形可由上述设计唯一确定.

4架无人机期望高度均设为1.5 m,初始期望位置分别设置为p1=[-0.75 2.5 1.5]Tm,p2=[0.75 2.5 1.5]Tm,p3=[-1 1.3 1.5]Tm,p4=[1 1.3 1.5]Tm.初始位置不满足期望队形.实验参数选取如下:k1=[1.25 1.25]T,k2=[1.25 1]T,λi=[2 2]T,(0)=[0 0]T,=[0.5 0.5]T,i=3,4.

在进行飞行实验时,首先令各无人机飞行到文中设置的初始位置.到达初始期望位置点后,作为Follower的无人机运行本文设计的控制算法,在仅利用方位信息的条件下完成编队的形成与跟踪任务;对2架作为Leader的无人机则通过位置信息进行位置跟踪控制,待到达初始期望位置后等待5 s,之后使2架Leader无人机在满足上述约束的情况下沿y方向进行vd=0.1 m/s的往返运动.飞行实验中4架无人机的位置如图4所示,图中虚线分别表示4架无人机的轨迹,实线为编队算法运行t0=16 s后4架无人机实时位置构成的队形,此时编队已处于前向移动状态,从图中可以看出,编队系统有效的完成了对期望移动队形的保持与跟踪任务.

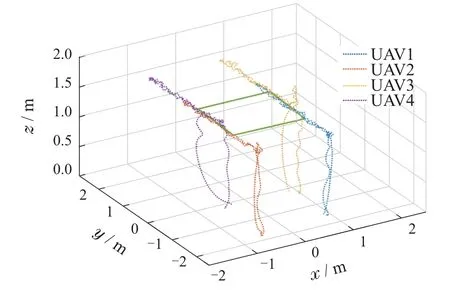
图4 三维位置图Fig.4 UAVs’position in 3D space

飞行过程中各方位信息由单位向量表示,实际方位信息与期望方位值差值(δij(t)=gij-)如图5所示,其中横轴为从各机体到达期望起始点时开始计算的所设计控制算法运行时间.纵轴为各机体相关的δij值.

为了更直观的表达各方位信息的控制效果,定义各Follower 方位总偏差为Vf,其随时间变化趋势如图6所示.从图5–6中可以看出,随着程序的运行,各方位逐渐收敛至其期望值,即多无人机系统在所设计的控制律作用下顺利完成了编队形成与跟踪任务.

图6 实验1: 各Follower无人机方位总偏差Fig.6 Case1: Total bearing errors for the followers

图7–8分别为Follower无人机3,4的控制输入曲线.从图中可以看出,控制量大小始终保持在一个合理的范围内.

图7 实验1: 无人机3控制量曲线图Fig.7 Case1: Control inputs of the UAV3

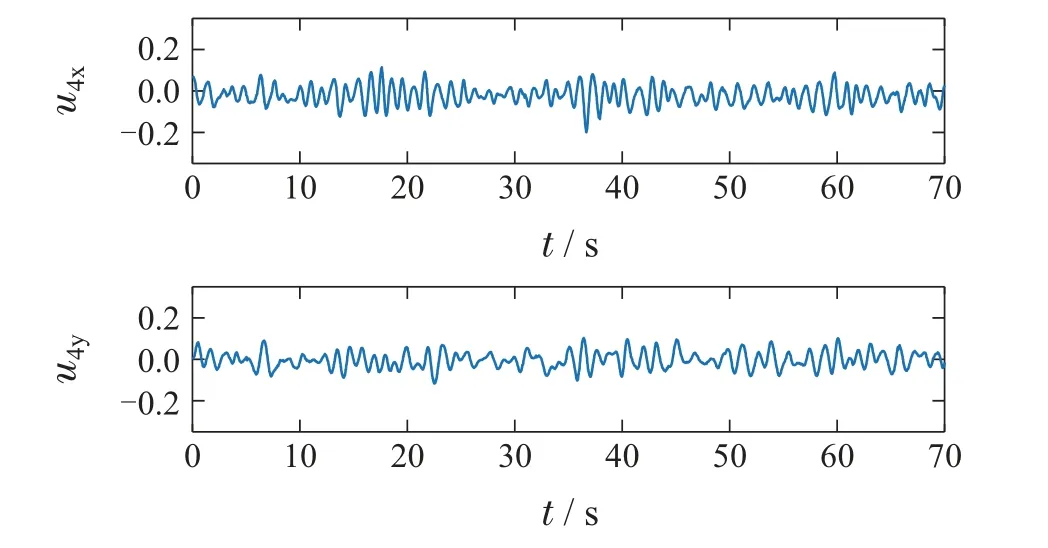
图8 实验1: 无人机4控制量曲线图Fig.8 Case1: Control inputs of the UAV4

对于由Leader–方位约束决定的编队队形,相同队形不同规模的队形(如Leader间的间距不同),对于同样的方位偏差δij(t)形成的编队效果不同.为了更直观的展示编队飞行效果,本文给出各Follower位置与期望位置偏差δpi(t)=pi(t)-(t)的曲线图.式中各Follower机体的期望位置(t)可由任意两架Leader的实时位置与期望方位约束计算得到.

从图9–10中可以看出,各Follower无人机在所设计控制器的作用下逐渐收敛到期望位置,并始终在期望位置附近的小范围内波动.由此可以直观的看出本文设计的控制器较好的完成了编队任务,并通过引入Leader无人机解决了位置漂移问题.

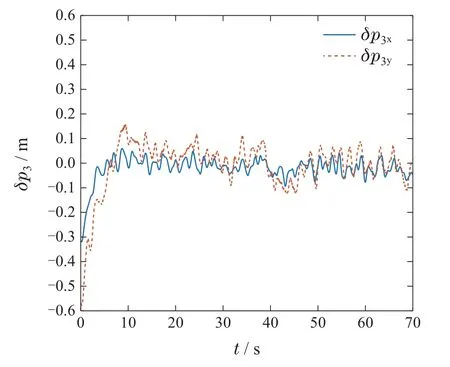
图9 实验1: 无人机3位置偏差图Fig.9 Case1: Position errors of the UAV3

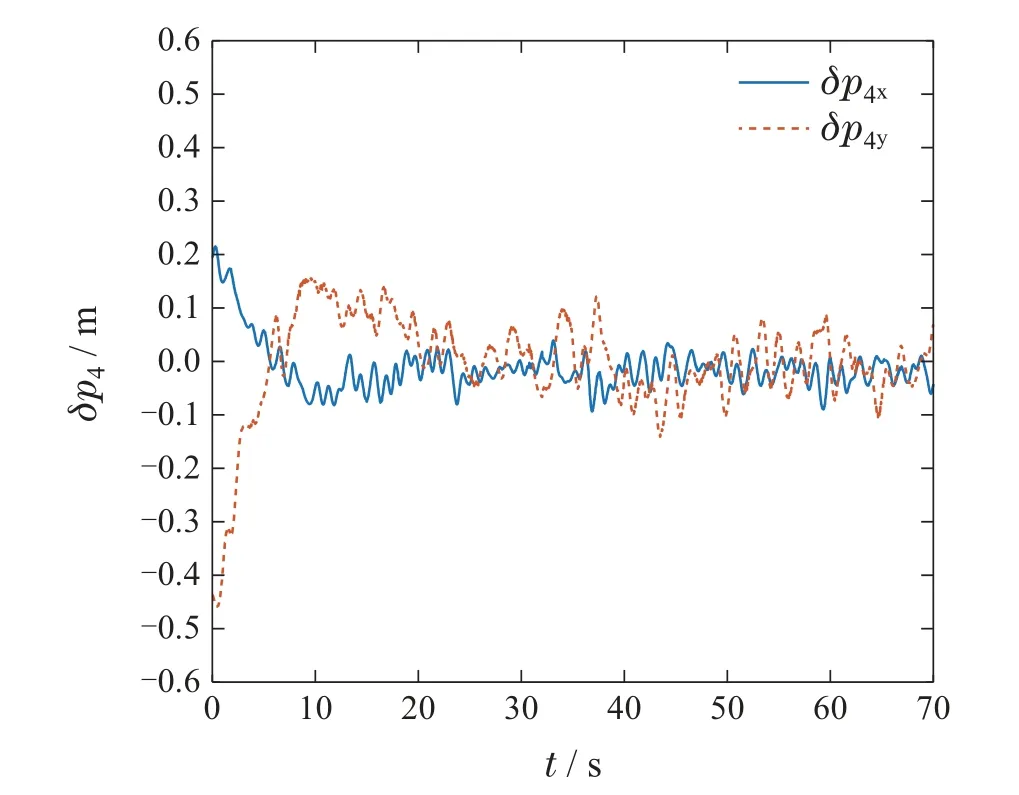
图10 实验1: 无人机4位置偏差图Fig.10 Case1: Position errors of the UAV4

5.3 实验2: PD对比试验

文献[20]采取Leader-Follower 式编队方法,针对双积分模型设计了一种基于方位信息的PD控制器来实现目标编队跟踪任务.根据文献[20]设计各Follower的控制输入为

选取参数kp=[2.5 2]T,kd=[2.5 2.5]T,按照第5.1,5.2节同样的实验环境与流程设计进行对比实验,实验数据结果如图11–15所示.

图11 实验2: 各Follower无人机方位总偏差Fig.11 Case2: Total bearing errors for the followers

对图6,9–10 与图11,14–15 中的数据的稳态过程进行定量对比分析,选取第10∼70 s的数据,分别对图中各量求取最大偏差和均方根误差,计算结果如表1与表2所示.对比图7–8与图12–13,可以发现在受到未知扰动,系统产生震荡时,本文设计的非线性控制器可以在更短的时间内用更合理的控制量进行矫正.对比表1与表2,可以发现实验1中∆i与δpi的最大偏差与均方根误差均为实验1 中的50%∼60%,这说明在本文所设计的控制器的作用下,多无人机系统形成的编队更趋近于期望编队,且波动更小.

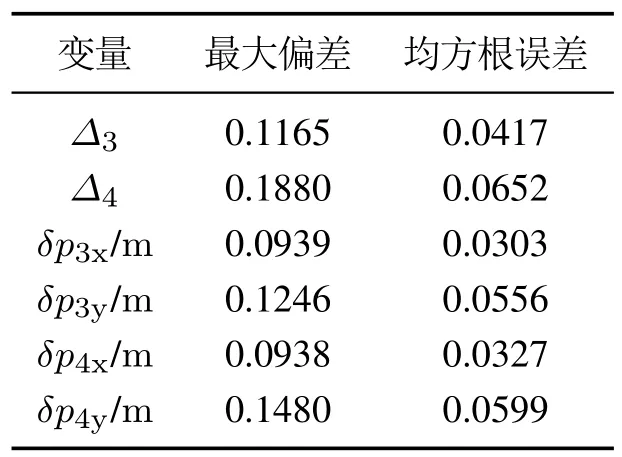
表1 本文控制器Table 1 Control design proposed in this paper

表2 文献[20]中设计的对比控制器Table 2 Control design proposed in[20]

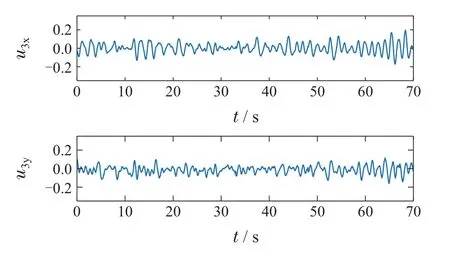
图12 实验2: 无人机3控制量曲线图Fig.12 Case2: Control inputs of the UAV3

图13 实验2: 无人机4控制量曲线图Fig.13 Case2: Control inputs of the UAV4

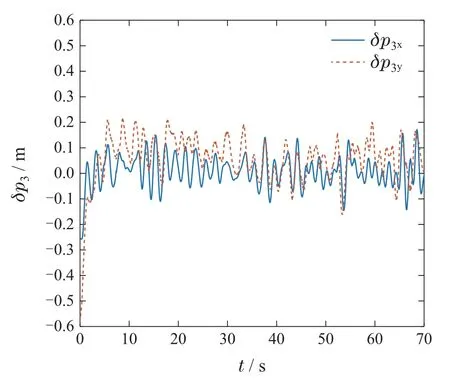
图14 实验2: 无人机3位置偏差图Fig.14 Case2: Position errors of the UAV3

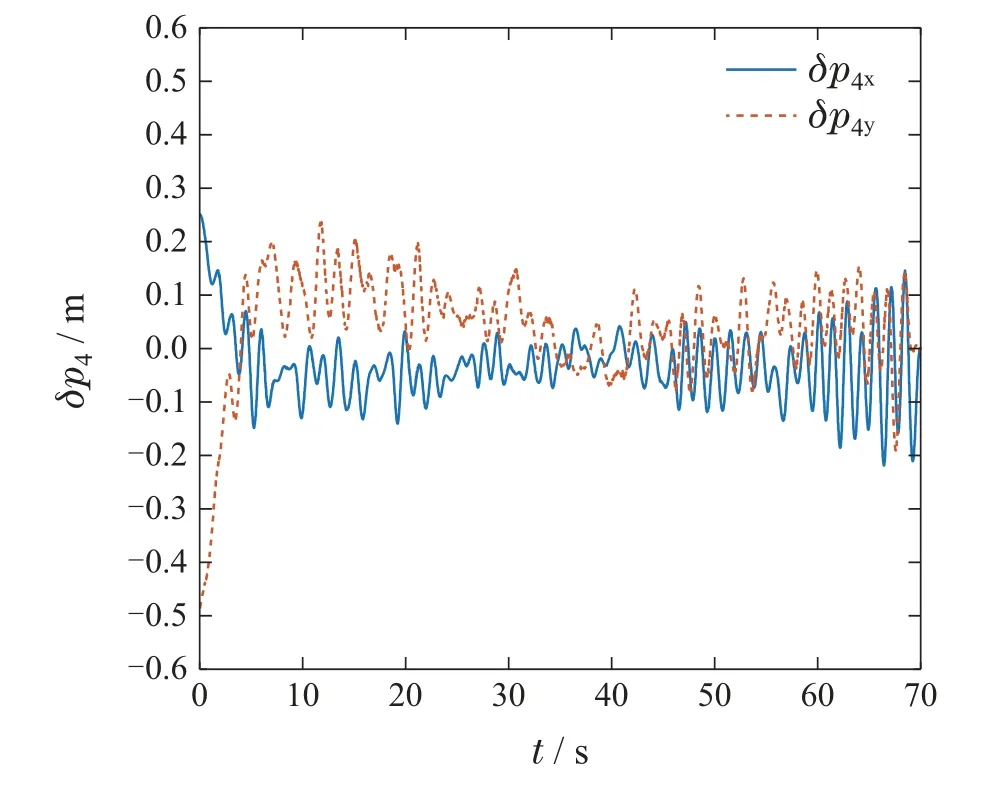
图15 实验2: 无人机4位置偏差图Fig.15 Case2: Position errors of the UAV4

结合上述图表,可以看出本文所设计的控制器相较于文献[20]中设计的控制器,在多无人机编队系统基于方位信息完成对目标编队的形成、保持和追踪任务时,具有更优异的性能.

6 结论

本文针对基于方位信息的多无人机系统编队控制问题,通过设置Leader引入位置信息来矫正飞行过程中的位置漂移.采用反步法引入自适应与鲁棒控制项抑制无人机飞行过程中存在的未知扰动与风阻,并基于Lyapunov方法对闭环系统的稳定性进行了证明.最后,在自主搭建的四旋翼无人机编队实验平台上进行了实际飞行实验,并与PD(proportional derivative)控制器进行了对比实验.实验结果表明本文设计的非线性控制器在对期望编队的形成、保持与跟踪过程中有着更好的表现.

在本文设计的基于方位信息的编队控制器中,未考虑实际飞行环境中存在障碍物的情况.在后续的工作中,将尝试不依赖位置信息的避障方法,实现基于方位信息的无人机编队的自主避障飞行控制.