面向FPGA便捷部署的智能模型预测控制

李星辰,赵斐然,孟庆辉,游科友

(1.清华大学自动化系,北京 100084;2.北京信息科学技术国家研究中心,北京 100084;3.潍柴动力股份有限公司,山东潍坊 261061)

1 引言

现场可编程逻辑门阵列(field programmable gate array,FPGA)是一种可编程逻辑器件,可根据需求改变芯片内存储单元、运算单元等电路单元的连接,实现定制化计算电路[1].与CPU,DSP等通用串行运算器件相比,易于并行化计算的FPGA可实现更大数据吞吐量、更低的延迟.与专用集成电路相比,FPGA具有更强的灵活性,为定制化算法快速设计提供了硬件基础[2].FPGA以其独特优势,可融合计算机视觉[3]、轨迹规划[4]、底层控制算法[5],实现一体化感知、决策、控制的智能终端,在无线通信[6]、自动驾驶[7]等领域具有广泛应用.

但FPGA使用较难掌握的硬件描述语言[8](hardware description language,HDL)编程,这限制了主要熟悉MATLAB,C++等高级语言的技术人员在FPGA上快速部署控制算法.近年来,直接通过高级语言代码生成HDL代码,即高层次综合(high level synthesis,HLS)备受关注[9].使用HLS不仅能极大缩短开发周期,且其代码的执行效率可超越人工[10].HDL代码的正确性是HLS 的关键,但HLS生成的代码不具有可读性,无法人工验证其正确性,所以如何闭环测试生成的代码是FPGA控制算法的挑战之一.

此外,先进控制算法往往需要在线实时求解优化问题[11],复杂的迭代求解方式并不能够完全发挥FPGA的并行计算优势.模型预测控制(model predictive control,MPC)随着采样时刻的推移进行滚动预测和优化,进而计算在性能指标下的最优控制律[12],但这需要较大的计算成本[13].使用FPGA可加速MPC优化问题的迭代求解,如在FPGA上定制化实现原对偶内点法[14]、对偶积极集法[15]、对数障碍内点法[16].但在线迭代求解算法难以充分发挥FPGA的并行计算优势,且无法保证迭代次数,占用资源高,如文献[17]在控制变量为1维、控制时域为3的情况下,需要96个DSP单元和20 k以上的查找表(lookup table,LUT)单元.

MPC控制律的求解本质是找到状态反馈和最优控制输入的映射关系,可使用神经网络[18–21]或基函数组合[22]高效求解MPC控制律.Karg和Lucia[20]的研究表明,神经网络拟合显式MPC控制律将极大减少所需参数量.文献[23]使用神经网络求得MPC优化问题的“好初始解”,降低了平均迭代次数,但并不能保证最坏情况下的加速效果.此外,现有研究[18–23]未考虑被控对象的时变特性,不能应用于带有时变参数的系统.

本文利用了神经网络的结构特点和FPGA的并行计算优势,提出基于神经网络的智能MPC及其FPGA快速实现方法,具有严格求解时间保证.克服人工编写HDL代码开发周期长、开发难度大的困难,基于HLS将神经网络的高级语言代码转换为HDL代码,并通过MATLAB-Modelsim联合仿真验证HDL代码的正确性,实现了便捷高效的FPGA部署.

首先,将时变系统的预测控制问题描述为具有线性约束的二次规划问题.然后,设计了便于并行部署的快速前向传播深度神经网络,通过离散采样并反复求解MPC优化问题得到数据集,并离线学习数据近似控制问题的最优解.同时,设计了一种PI-MPC串级控制方法,以应对模型参数误差.以此智能MPC框架为基础,提出了基于HLS的高效HDL生成方法,适用于MATLAB的HDL软件级联合测试流程,及FPGA快速部署、测试验证方案.最后,将所提方法应用于控制频率高达10 kHz的永磁同步电机电流环以及四旋翼无人机轨迹跟踪,FPGA硬件在环实验验证了所提方法的快速性及鲁棒性.因此,本文的贡献主要有: 1)提出了基于深度神经网络的智能PI-MPC串级控制方法及基于HLS的高效HDL生成方法和MATLAB-Mode-lsim联合HDL测试流程;2)在FPGA上提供了具有严格求解时间保证的智能MPC高控制频率便捷部署方案.

本文剩余部分结构如下: 第2节讨论MPC及其二次规划(quadratic programming,QP)问题形式;第3节提出基于深度神经网络的智能MPC方法;第4节设计基于HLS的高效HDL生成方法、适用于MATLAB的HDL软件级联合测试流程;第5节将智能MPC应用在内置式永磁同步电机电流环(10 kHz高速控制系统)中;第6节将智能MPC应用在四旋翼无人机的轨迹跟踪控制(高维控制系统)中,并给出FPGA快速部署、测试验证方案,硬件在环(hardware in the loop,HiL)测试验证了所提方法的有效性;第7节给出结论.

2 时变系统的MPC及其QP形式

2.1 时变系统的MPC问题

考虑如下带约束的时变离散系统:

其中:xk|t为t时刻通过模型预测t+k时刻的状态向量,uk|t为t+k时刻的控制向量,N为预测时长,P≥0,Q≥0,R>0,=xTPx.由于难以获得未来的时变参数,st在t时刻固定,测试时不再变化.固定的st在N较小时具有较好的近似效果,因此适用于时变参数变化缓慢的系统.

2.2 MPC的QP形式

问题(3)可转化为一个具有线性约束的二次规划问题(5).根据式(1)得到

进而,优化问题(3)可以转化为

3 基于神经网络的快速MPC

3.1 QP的快速求解

求解优化问题(5)即计算函数gMPC,但这需要较大计算成本.直接在FPGA 上部署迭代式QP 求解算法[14–17],不仅占用资源高,而且没有严格的求解时间保证.

本文离线采样状态反馈并反复求解MPC优化问题得到数据集,并利用FPGA并行计算优势设计深度神经网络,进而离线对神经网络进行训练,在线仅需进行神经网络正向传播即可得到控制输入,提供了有严格求解时间保证、占用资源少的高控制频率FPGA部署方案.

3.2 神经网络的设计

为了在保证拟合效果的同时,降低FPGA的资源占用,需对神经网络进行结构设计.FPGA使用基本逻辑单元构建电路,较难处理非线性函数的计算,激活函数采用形式简单的分段线性函数,如常用的ReLU[24],LeakyReLU[25].为了复用电路模块,采用多层全连接网络实现神经网络,且隐层的节点数目相同.gNN的定义为

其中:σ(x)=LeakyReLU(x)=max{x,0.01x}为非线性激活函数,Li(x)=Wix+bi为线性函数,θ={W1,···,WK,b1,···,bK}为参数的集合.Lin和Lout为缩放层(scaling layer),将输入进行归一化,并将输出缩放到合适范围.

神经网络的整体结构如图1所示,为保证神经网络输出都在可行集内,在神经网络最后添加一投影层,根据神经网络输入将神经网络输出投影到多面体可行集内.由于神经网络输出仅为一个时刻的控制量,投影的计算量小.

3.3 神经网络的离线训练

神经网络训练目标为gNN尽可能接近gMPC,同时gNN在可行集内,构建如下带约束的监督学习问题:

3.4 PI-MPC串级控制

为了提高控制性能,并应对系统建模时可能出现的模型偏差,在神经网络MPC前添加积分环节或PI控制,当存在静态误差时可以及时调整神经网络的目标值,从而减少静态误差,并提高控制鲁棒性.实验表明,该控制方案结合了PI控制的历史信息和MPC的未来信息,实现了比单独PI控制或单独MPC更好的控制效果.

PI控制的输入为目标状态与状态反馈的差值,控制框架如图2.对于具有n维状态变量的系统,对每一个维度均设置前置PI控制,此时每个PI控制的作用为微调MPC某个维度的参考信号.

图2 控制设计原理框架Fig.2 Control design framework

4 MPC的FPGA快速实现与测试

4.1 基于HLS的HDL生成与Modelsim验证

为克服人工编写HDL代码开发周期长、开发难度大的困难,本文使用Xilinx Vitis HLS工具,将C++高级语言代码直接转换成HDL代码,极大缩短了开发时间.MATLAB为功能强大的通用建模和控制系统仿真工具[26],本文提出了适用于MATLAB的HDL软件级联合测试流程,被控对象和控制器原型设计均可以在MATLAB中完成,不用使用其他语言重新编写.

为保证控制算法的硬件描述语言版本与原始版本功能相同,本文提出一套基于MATLAB仿真模型和Xilinx HLS 的HDL 生成与测试流程,如图3.使用MATLAB 可以方便地进行控制算法设计,但为了生成HDL代码,需要编写与MATLAB代码功能相同的C++代码.为验证C++代码和MATLAB代码的一致性,在MATLAB R2020a/Simulink环境下通过Xilinx公司开发的Model Composer进行验证对比仿真.

图3 HDL生成与测试流程图Fig.3 HDL Generation and testing flowchart

确认C++代码调试通过后,在代码中添加Xilinx HLS相关的编译指令,设置端口、控制协议、流水线、循环展开、存储结构等硬件属性,通过Xilinx Vitis HLS 2020.1将带有编译指令的C++代码转换成硬件语言描述的IP核.在MATLAB HDL Verifier中配置相关脚本和仿真属性,并在Simulink中对比仿真HDL代码和MATLAB代码.当两者功能一致时,IP核的功能与原始控制算法完全相同,后续只需进行FPGA原理图的综合和部署.

该流程通过对比仿真、MATLAB-Modelsim联合仿真验证生成代码的正确性,相比手动编写HDL代码,极大提高了编程效率,缩短开发时间.

4.2 FPGA测试系统实现

为测试智能MPC对应IP核在FPGA芯片上的真实运行情况,本文使用Xilinx Zynq UltraScale+MPSoC ZCU-102开发套件进行FPGA测试系统的搭建.ZCU 102开发板具有丰富的外设和高性能接口,其ZYNQ芯片型号为XCZU9EG-FFVB1156-2-E.

FPGA测试系统实现方案如图4.测试系统主要分为3个部分: PL系统、PS程序、PC上位机.PL系统为FPGA硬件电路构成,主要运行控制器的IP核,通过Vivado软件进行设计开发.PS为Arm核上的裸机程序,进行与PL系统、PC上位机的通信,控制测试流程及并运行永磁同步电机(permanent magnet synchronous motor,PMSM)被控对象.PS通过Vitis软件进行设计开发,PL与PS通过AXI总线连接.PC上位机运行MATLAB程序,使用波特率为115200 bps的COM端口向Arm核发送控制指令,Arm核上程序通过传输速率为1G bps的以太网口和以太网线向PC上位机发送运行数据.

图4 FPGA测试系统实现方案Fig.4 FPGA test system implementation scheme

5 智能MPC在高控制频率系统中的应用

本节将智能MPC应用到PMSM的电流环控制上.由于PMSM机械时间常数远远大于电气时间常数,通常采用如图5的双闭环控制(上标r表示变量的参考值),本文的控制目标为电流环的跟踪控制,由于其动态变化很快,其控制频率要求高达10 kHz.

图5 PMSM的一种双闭环控制框图Fig.5 A double closed-loop control of PMSM

针对永磁同步电机电流环的控制,文献[13]使用德州仪器F28335 Delfino DSP在线求解MPC优化问题,把永磁同步电机电流环控制计算时间稳定在300 us以内.文献[27]使用具有双核2 GHz实时处理器的dSPACE,调用开源求解器qpOASES在线求解MPC优化问题.实验表明,在该硬件配置下最坏情况需要大概70 us的计算时间,但无法给出严格的求解时间保证.而且文献[27]使用的硬件性能较强,价格昂贵,难以低成本部署以实现产品化.

算法特性和硬件环境的匹配是控制算法部署最重要的问题之一,本文综合神经网络结构和FPGA硬件特性,提出基于神经网络的智能模型预测方法并使用FPGA进行快速实现.由于FPGA定制硬件电路程序循环周期数、FPGA时钟频率是确定不变的,因此具有严格求解时间保证(小于100 us,可以实现10 kHz稳定控制频率),且占用FPGA资源少,可以使用价格低廉、存算资源有限的FPGA芯片部署.

5.1 永磁同步电机数学模型

内置式永磁同步电机的数学模型是非线性、时变的.在d-q旋转坐标系下,其状态为d轴电流id,q轴电流iq,转速ωe.其数学模型微分方程表述如式(9).

其中:ud,uq分别为d轴、q轴电压,Ld为定子d轴电感,Lq为定子q轴电感,Rs=0.0249 Ω为定子电阻,φr=0.02932 Wb 为转子磁链,np=6 为极对数,J=1.036 Kg·m2为转动惯量,Te为输出转矩,TL为负载转矩.Ld,Lq的值取决于id,iq,其函数关系是非线性的.

在本文中,主要实现永磁同步电机电流环的控制,电流环系统离散预测模型为

控制量ud,uq满足将约束条件进行线性化,约束边界从圆变为圆内接正12边形,线性化约束的表达式如式(12).

5.2 基于神经网络的智能MPC

使用MALTAB R2020b自带函数quadprog进行求解,指定方法active-set.在CPU 型号为i5-8400,内存16 G,Windows 10系统计算机上求解10000次该优化问题,平均单次用时1.3 ms,不能满足Ts=10-4s的要求.

为了得到神经网络训练所需数据集,首先确定状态、参考信号和时变参数的上下界,如表1.在id,iq,umax的上下界范围内均匀采样变量的值,可还原出优化问题(5).求解该优化问题,得到第一步对应的最优控制.反复随机采样变量的值,并得到对应最优控制量,最终构成神经网络训练的数据集,数据集样本数为3×106.

表1 变量的上下界Table 1 Upper and lower bounds of variables

选取数据集中5%的样本为验证集,其余95%为训练集.选取隐层数量为5,隐层宽度为50,激活函数为LeakyReLU 的神经网络.设定ωe=1591.54 r/min,id=-100 A,iq=-100 A,umax=346.41 V,绘制ud随着,变化的三维图如图6,MPC和神经网络两者非常接近.

图6 MPC和神经网络输出三维图Fig.6 MPC and neural network output 3D graph

对不同参数数量、深度、激活函数的神经网络进行训练,最终选取隐层数量为5,隐层宽度为50,激活函数为LeakyReLU的神经网络,有优越的训练效果.其训练集均方平均损失为6.18×10-5,验证集均方平均损失为6.34×10-5.

5.3 HDL生成

使用不同的编译指令生成的硬件性能不同,为保证控制频率的同时尽可能减低资源占用,本文对HLS编译指令进行了优化设计.

运行时间和资源占用情况如表2和表3.编号1到编号6使用了不同的HLS编译指令和计算顺序,因此生成硬件的运行时间和资源占用不同.编号1、编号2对程序整体流水线化.计算神经网络矩阵运算时,编号1,3,5先沿矩阵的第1维索引乘加,编号2,4,6先沿矩阵的第2维索引乘加.编号5,6在矩阵乘向量运算的两层for循环处设置流水线.

表2 不同优化方案对应IP核运行时间情况表Table 2 IP core running time corresponding to different optimization schemes

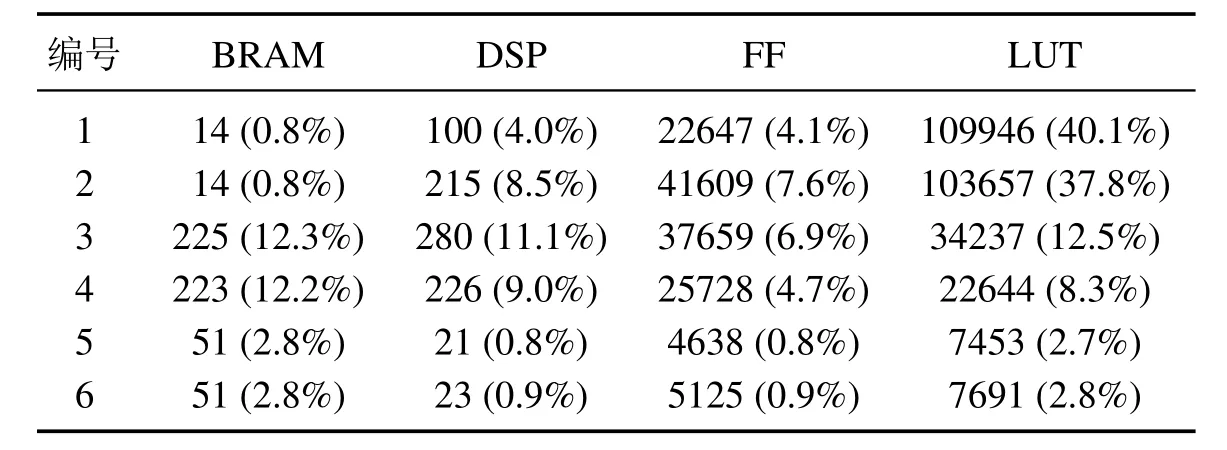
表3 不同优化方案对应IP核资源占用情况表Table 3 IP core resource occupancy correspondingto different optimization schemes

表2中,编号1,2未能实现200 MHz(5 ns)的目标时钟,只能以更低频率时钟运行,但控制频率仍可达到50 kHz以上.编号3,4,5,6均能实现200 MHz的目标时钟,但编号5未能实现10 kHz的控制频率.表3中,编号1,2占用资源较多,编号5,6的BRAM和LUT使用量均为3%以下,数字信号处理单元(digital singnal Processor,DSP)和触发器(flip-flop,FF)的使用量均为1%以下,占用资源很少.

最终采用编号6的HLS生成方案,该方案能够实现10 kHz的控制频率且资源占用很少,其运行时间分析和资源占用分析示意图如图7,其中隐层的正向传播占去86.5%的计算时间.

图7 运行时间分析和资源占用分析示意图Fig.7 Run times and resource occupancy analysis

5.4 控制效果验证情况

FPGA控制器和原始MPC极为相近,控制效果相当,具有优越控制效果和高控制频率.具体仿真设置为:=-213.77 A,umax=346.41 V,在恒定转速ωe=900 r/min下进行测试.在t=0.3 s时,设置变为218.92 A,0.7 s时变为0.并将FPGA控制器(实时测试)与原始MPC(在MATLAB仿真环境下进行测试)进行对比.iq跟随情况如图8.

图8 q轴电流跟随图Fig.8 q-axis current following diagram

FPGA控制器在各种参数误差工况下均保持了优越的控制性能.具体仿真设置为:=-191.67 A,umax=346.41 V,在恒定转速ωe=300 r/min下进行测试.t=0.3 s 时,设置变为375.90 A,0.7 s时变为0.在PMSM模型的Rs,Ld,Lq参数添加20%的误差,观察在有误差的PMSM模型下的控制跟随效果.iq跟随情况如图9.

图9 具有模型参数误差时q轴电流跟随图Fig.9 q-axis current following diagram with model parameter errors

在不同工况下,智能MPC都能够满足最大电压约束,如图10.

图10 具有模型参数误差时控制电压图Fig.10 Control input voltage diagram with model parameter errors

6 智能MPC在高维系统中的应用

本节将智能MPC应用到四旋翼无人机(unmanned aerial vehicle,UAV)的轨迹跟踪控制中.在实际环境中,无人机的工作空间通常具有障碍物,因此要求四旋翼无人机能够在安全避障的情况下实现特定任务,例如到达指定地点、以恒定速度环绕移动目标.

为验证智能MPC方法在高维、带约束系统中的有效性,本节针对快速穿越障碍物区域的任务,研究具有12维状态的四旋翼无人机的轨迹跟踪及避障问题.

6.1 四旋翼无人机数学模型

本文采用文献[28]中基于Newton-Euler方法给出的四旋翼无人机的数学模型

其中:ξ=[x(t)y(t)z(t)]T为四旋翼无人机在世界坐标系中的三维空间位置,η=[ϕ(t)θ(t)ψ(t)]T为世界坐标系中的欧拉角,m为无人机的质量,g=[0 0-9.81 m/s2]T为重力加速度,R(η)为机身坐标系到世界坐标系的旋转矩阵,dx,dy,dz为速度阻尼系数,J-1(η)为雅可比矩阵的逆矩阵,C(η,)为科里奥利矩阵.

机身受到旋翼的力τ1和力矩τ2取决于4个旋翼的旋转速度

其中:u=[u1(t)u2(t)u3(t)u4(t)]为与旋翼旋转速度相关的控制量,k1,k2,k3为常系数.

令x=[ξ;η;;],无人机模型为=f(x,u).该模型为非线性模型,使用显式欧拉法将该模型线性化,并转化为LPV模型如下:

取采样周期Ts=0.1 s,上式为

6.2 智能MPC设计与FPGA测试

为保证控制效果,令N=10,上式权重矩阵为

且控制量具有约束04×1≤u≤12×14×1.

此外,为了避免与障碍物碰撞,设置如图11所示的时变状态约束.为保证无人机的安全,距离无人机周围r=0.3 m的位置不能出现障碍物,即以无人机为中心、半径为r的圆与障碍物不相交.在每个时刻,将无人机与障碍物不相交简化为圆在某个半平面内,该半平面由该时刻的参考位置确定.该约束可写为GtxNp|t≤gt,为时变约束.当无人机的参考位置位于左上角时,可行域在左边,无人机的预测位置应该在这可行域1内.当无人机来到下方时,则应该在可行域2内.

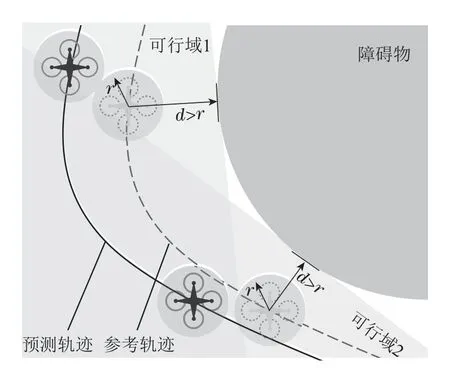
图11 无人机避障约束示意图Fig.11 Diagram of obstacle avoidance constraint for UAV

为了得到神经网络训练所需数据集,本文给定不同的随机参考轨迹,分别使用上述MPC进行控制,并收集状态参考轨迹,状态轨迹{x0,x1,···,xT}和控制轨迹{u0,u1,···,uT}.将参考轨迹的第1到3维抽出记为,并将状态约束不等式两边的Gt和gt的非零项也作为输入,构造输入输出对([xk;;Gt;gt],uk),输入为18维、输出为4维.收集2.8×106个输出输出对,得到训练数据集.

同样选择5%的数据集作为验证集,其余95%为训练集.选取隐层数量为4,隐层宽度为80,激活函数为LeakyReLU的神经网络使用Adam优化器进行训练.其训练集均方损失为3.13×10-4,验证集均方损失为3.15×10-4.

在HDL生成时,使用第5.3节中的最优配置方案,得到表4和表5.控制算法在FPGA上运行仅需0.11 ms,且占用FPGA资源少于4%.

表4 IP 核运行时间情况表Table 4 IP core running time

表5 IP 核资源占用情况表Table 5 IP core resource occupancy

同样地,硬件电路程序循环周期数、FPGA时钟频率确定不变.因此无人机智能MPC具有严格求解时间保证,其求解频率能严格稳定在8.846 kHz,远超采样频率.且该方案占用FPGA资源少,这说明该方法应用在更复杂的被控对象和控制任务上有很大潜力.

6.3 控制效果验证情况

为验证算法完成快速穿越障碍物区域任务的能力,人工指定一条参考轨迹,并在每个时刻对控制量u添加服从正态分布N(04×1,0.2×I4×4)的噪声.将无状态约束的MPC,FPGA上的智能MPC,PID这3种控制律的控制效果进行对比.轨迹跟踪情况如图12.

可以看到,添加了状态约束的FPGA控制器的能够始终保持与障碍物的安全距离,无状态约束的MPC和PID将会撞向障碍物,这验证了智能MPC处理约束的有效性.

在轨迹跟踪中,FPGA计算得到的控制量如图13,可见其满足控制约束.

图13 轨迹跟踪控制量变化图Fig.13 Control input diagram of trajectory tracking

7 结论

本文以FPGA为实现平台,研究了不精确时变系统MPC的FPGA快速实现问题.为避免QP迭代求解资源占用高、求解时间不确定的问题,使用适用于FPGA的深度神经网络求解MPC优化问题,并考虑时变参数.为克服人工编写HDL代码开发难度大的困难,本文使用HLS工具生成HDL代码,并提出了MATLABModelsim联合仿真测试流程,以确保代码转换的一致性.将所提方法应用于采样频率高达10 kHz的PMSM电流环控制和高维度的UAV轨迹跟踪控制,FPGA在环测试验证了有效性.未来可进一步研究神经网络参数量与MPC问题复杂性的理论关系,为神经网络结构设计提供理论参考.此外,为提高鲁棒性,可探讨Tube-based MPC等方法的FPGA快速部署方案.