不对称约束多人非零和博弈的自适应评判控制

李梦花,王 鼎,乔俊飞

(北京工业大学信息学部,北京 100124;计算智能与智能系统北京市重点实验室,北京 100124;智慧环保北京实验室,北京 100124;北京人工智能研究院,北京 100124)

1 引言

自适应动态规划(adaptive dynamic programming,ADP)方法由Werbos[1]首先提出,该方法结合了动态规划、神经网络和强化学习,其核心思想是利用函数近似结构来估计最优代价函数,从而获得被控系统的近似最优解.在ADP方法体系中,动态规划蕴含最优性原理提供理论基础,神经网络作为函数近似结构提供实现手段,强化学习提供学习机制.值得注意的是,ADP方法具有强大的自学习能力,在处理非线性复杂系统的最优控制问题上具有很大的潜力[2–7].此外,ADP作为一种近似求解最优控制问题的新方法,已经成为智能控制与计算智能领域的研究热点.关于ADP的详细理论研究以及相关应用,读者可以参考文献[8–9].本文将基于ADP的动态系统优化控制统称为自适应评判控制.

近年来,微分博弈问题在控制领域受到了越来越多的关注.微分博弈为研究多玩家系统的协作、竞争与控制提供了一个标准的数学框架,包括二人零和博弈、多人零和博弈以及多人非零和博弈等.在零和博弈问题中,控制输入试图最小化代价函数而干扰输入试图最大化代价函数.在非零和博弈问题中,每个玩家都独立地选择一个最优控制策略来最小化自己的代价函数.值得注意的是,零和博弈问题已经被广泛研究.在文献[10]中,作者提出了一种改进的ADP方法来求解多输入非线性连续系统的二人零和博弈问题.An等人[11]提出了两种基于积分强化学习的算法来求解连续时间系统的多人零和博弈问题.Ren等人[12]提出了一种新颖的同步脱策方法来处理多人零和博弈问题.然而,关于非零和博弈[13–14]的研究还很少.此外,控制约束在实际应用中也广泛存在.这些约束通常是由执行器的固有物理特性引起的,如气压、电压和温度.因此,为了确保被控系统的性能,受约束的系统需要被考虑.Zhang等人[15]发展了一种新颖的事件采样ADP方法来求解非线性连续约束系统的鲁棒最优控制问题.Huo等人[16]研究了一类非线性约束互联系统的分散事件触发控制问题.Yang和He[17]研究了一类具有不匹配扰动和输入约束的非线性系统事件触发鲁棒镇定问题.这些文献考虑的都是对称约束,而实际应用中,被控系统受到的约束也可能是不对称的[18–20],例如在污水处理过程中,需要通过氧传递系数和内回流量对溶解氧浓度和硝态氮浓度进行控制,而根据实际的运行条件,这两个控制变量就需要被限制在一个不对称约束范围内[20].因此,在控制器设计过程中,不对称约束问题将是笔者研究的一个方向.

到目前为止,关于具有控制约束的微分博弈问题,有一些学者取得了相应的研究成果[12,21–23].但可以发现,具有不对称约束的多人非零和博弈问题还没有学者研究.同时,在多人非零和博弈问题中,相关的耦合Hamilton-Jacobi(HJ)方程是很难求解的.因此,本文针对一类连续时间非线性系统的不对称约束多人非零和博弈问题,提出了一种自适应评判控制方法来近似求解耦合HJ方程,从而获得被控系统的近似最优解.本文的主要贡献如下: 1)首次将不对称约束应用到连续时间非线性系统的多人非零和博弈问题中;2)提出了一种新颖的非二次型函数来处理不对称约束问题,并且当系统状态为零时,最优控制策略是不为零的,这与以往不同;3)在学习期间,用单一评判网络结构代替了传统的执行–评判网络结构,并且提出了一种新的权值更新规则;4)利用Lyapunov方法证明了评判网络权值近似误差和系统状态的一致最终有界(uniformly ultimately bounded,UUB)稳定性.

2 问题描述

考虑以下具有不对称约束的N–玩家连续时间非线性系统:

其中:x(t)∈Ω ⊂Rn是状态向量且x(0)=x0为初始状态,Rn代表由所有n-维实向量组成的欧氏空间,Ω是Rn的一个紧集;uj(t)∈Tj ⊂Rm为玩家j在时刻t所选择的策略,且Tj为

假设1非线性系统(1)是可控的,并且x=0是被控系统(1)的一个平衡点.此外,∀j ∈N,f(x)和gj(x)是未知的Lipschitz函数且f(0)=0,其中集合N={1,2,···,N},N≥2是一个正整数.

假设2∀j ∈N,gj(0)=0,且存在一个正常数bgj使‖gj(x)‖≤bgj,其中‖·‖表示在Rn上的向量范数或者在Rn×m上的矩阵范数,Rn×m代表由所有n×m维实矩阵组成的空间.

注1假设1–3是自适应评判领域的常用假设,例如文献[6,13,19],是为了保证系统的稳定性以及方便后文中的稳定性证明,其中假设3出现在后文中的第3.2节.

定义与每个玩家相关的效用函数为

其中U={u1,u2,···,uN}并且Qi是一个对称正定矩阵.此外,为了处理不对称约束问题,令Sj(uj)为

其中αj和βj分别为

因此,与每个玩家相关的代价函数可以表示为

其中i ∈N.为了方便,将Ji(x0,U)简写为Ji(x0).于是,每个玩家的最优代价函数为

在本文中,如果一个控制策略集的所有元素都是可容许的,那么这个集合是可容许的.

定义1(容许控制[24])如果控制策略ui(x)是连续的,ui(x)可以镇定系统(1),并且Ji(x0)是有限的,那么它是集合Ω上关于代价函数(6)的可容许控制律,即ui(x)∈Ψ(Ω),i ∈N,其中,Ψ(Ω)是Ω上所有容许控制律的集合.

对于任意一个可容许控制律ui(x)∈Ψ(Ω),如果相关代价函数(6)是连续可微的,那么非线性Lyapunov方程为

其中,Hamiltonian函数Hi(x,U,∇(x))为

注2根据式(2)和式(5),能推导出βi≠0,即≠0,又根据式(12)可知(0)≠0,i ∈N.因此,为了保证x=0是系统(1)的平衡点,在假设2中提出了条件∀j ∈N,gj(0)=0.

将式(12)代入式(10),耦合HJ方程又能表示为

如果已知每个玩家的最优代价函数值,那么相关的最优状态反馈控制律就可以直接获得,也就是说式(13)是可解的.可是,式(13)这种非线性偏微分方程的求解是十分困难的.同时,随着系统维数的增加,存储量和计算量也随之以指数形式增加,也就是平常所说的“维数灾”问题.因此,为了克服这些弱点,在第3部分提出了一种基于神经网络的自适应评判机制,来近似每个玩家的最优代价函数,从而获得相关的近似最优状态反馈控制策略.

3 自适应评判控制设计

3.1 神经网络实现

本节的核心是构建并训练评判神经网络,以得到训练后的权值,从而获得每个玩家的近似最优代价函数值.

首先,根据神经网络的逼近性质[25],可将每个玩家的最优代价函数(x)在紧集Ω上表示为

其中:Wi ∈Rδ是理想权值向量,σi(x)∈Rδ是激活函数,δ是隐含层神经元个数,ξi(x)∈R是重构误差.同时,可得出每个玩家的最优代价函数梯度为

将式(15)代入式(12),有

值得注意的是,式(14)中的理想权值向量Wi是未知的,也就是说式(16)中的(x)是不可解的.因此,构建如下的评判神经网络:

考虑式(19),近似的最优控制律为

3.2 稳定性分析

本节的核心是通过利用Lyapunov方法讨论评判网络权值近似误差和闭环系统状态的UUB稳定性.这里,给出以下假设:

定理1考虑系统(1),如果假设1–3成立,状态反馈控制律由式(20)给出,且评判网络权值通过式(22)进行训练,则评判网络权值近似误差是UUB稳定的.

证选取如下的Lyapunov函数:

计算L1i(t)沿着式(23)的时间导数,即

根据假设3,有

其中λmin(·)表示矩阵的最小特征值.因此,当不等式

证毕.

定理2考虑系统(1),如果假设1–3成立,状态反馈控制律由式(20)给出,且评判网络权值通过式(22)进行训练,则系统状态x(t)是UUB稳定的.

证选取如下的Lyapunov函数:

考虑式(13),有

同时,根据假设2–3,有

4 仿真结果

考虑如下的3–玩家连续时间非线性系统:

其中:x(t)=[x1x2]T∈R2是状态向量,u1(x)∈T1={u1∈R:-1 ≤u1≤2},u2(x)∈T2={u2∈R:-0.2 ≤u2≤1}和u3(x)∈T3={u3∈R:-0.4 ≤u3≤0.8}是控制输入.

令Q1=2I2,Q2=1.8I2,Q3=0.3I2,其中I2代表2× 2维单位矩阵.同时,根据式(5)可知,α1=1.5,β1=0.5,α2=0.6,β2=0.4,α3=0.6,β3=0.2.因此,与每个玩家相关的代价函数可以表示为

执行学习过程,本文发现每个玩家的评判神经网络权值分别收敛于[6.9091 2.9904 6.6961]T,[4.8901 2.2347 5.2062]T,[1.7945 0.3321 2.4583]T.在60个时间步之后去掉探测噪声,每个玩家的评判网络权值收敛过程如图1–3所示.然后,将训练好的权值代入式(20),能得到每个玩家的近似最优控制律,将其应用到系统(39),经过10个时间步之后,得到的状态轨迹和控制轨迹分别如图4–5所示.由图4可知,系统状态最终收敛到了平衡点.由图5可知,每个玩家的控制轨迹都没有超出预定的边界,并且可以观察到u1,u2和u3分别收敛于0.5,0.4和0.2.综上所述,仿真结果验证了所提方法的有效性.

图1 玩家1的评判网络权值收敛过程Fig.1 Convergence process of the critic network weights for player 1

图2 玩家2的评判网络权值收敛过程Fig.2 Convergence process of the critic network weights for player 2

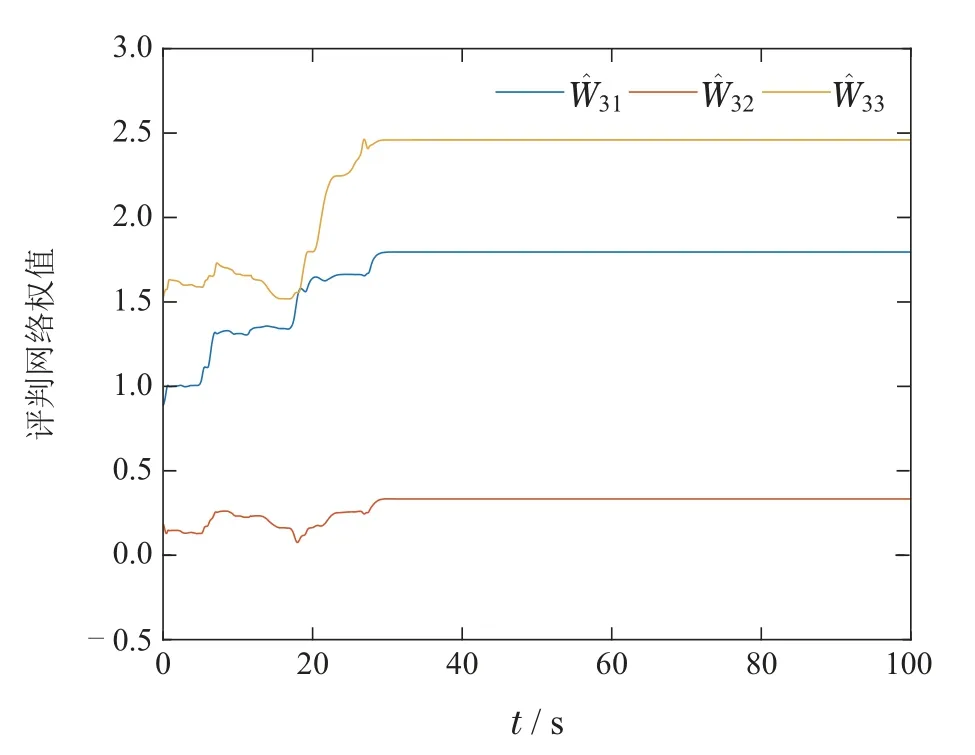
图3 玩家3的评判网络权值收敛过程Fig.3 Convergence process of the critic network weights for player 3

图4 系统(39)的状态轨迹Fig.4 State trajectory of the system(39)

图5 系统(39)的控制轨迹Fig.5 Control trajectories of the system(39)

5 结论

本文首次将不对称约束应用到连续时间非线性系统的多人非零和博弈问题中.首先,获得了最优状态反馈控制律和耦合HJ方程,并且为了解决不对称约束问题,建立了一种新的非二次型函数.值得注意的是,当系统状态为零时,最优控制策略是不为零的.其次,由于耦合HJ方程不易求解,提出了一种基于神经网络的自适应评判算法来近似每个玩家的最优代价函数,从而获得相关的近似最优控制律.在实现过程中,用单一评判网络结构代替了经典的执行–评判结构,并且建立了一种新的权值更新规则.然后,利用Lyapunov理论讨论了评判网络权值近似误差和系统状态的UUB稳定性.最后,仿真结果验证了所提算法的可行性.在未来的工作中,会考虑将事件驱动机制引入到连续时间非线性系统的不对称约束多人非零和博弈问题中,并且将该研究内容应用到污水处理系统中也是笔者的一个重点研究方向.