基于机械虹膜机构的新型摆动泵及其流场分析*
李 强,孟利民,2*,周 琪,曹旭峰
(1.安徽理工大学 机械工程学院,安徽 淮南 232001;2.浙江大学 流体动力与机电系统国家重点实验室,浙江 杭州 310027)
0 引 言
由于液压传动的独特优点,从民用到国防,从一般传动到高精度控制系统,液压传动系统在各领域都得到了广泛应用[1]。
摆动泵是一类液压泵。相比于其他类型的泵,摆动泵具有效率高、自吸能力强、运行平稳、结构简单等优点,特别适合于输送黏性流体介质或者多相流介质,在石油化工、医药、食品等行业中的运用相对较为广泛[2-3]。
近几十年来,国内外众多学者已对摆动泵开展了广泛的研究。
王子祥等人[2]通过改变摆动泵的转子形状,提出了一种新型的摆动泵模型,该模型可为摆动泵减小流量脉动的研究提供一定的参考。张朦淅等人[4]研究了不同叶片数下翅板摆动泵内部流场的变化情况,研究结果表明,片数为2时翅板摆动泵的工作性能最好。侯勇俊等人[5]提出了一种凸轮和齿扇、齿条复合驱动的新型往复泵,三缸往复泵的流量脉动率仅为1.68%。魏琦等人[6]推导了单作用往复泵排量不均度及活塞惯性力的解析式,得到了排量不均度随往复泵缸数及曲柄连杆比的变化曲线,为单作用往复泵结构参数的设计和活塞疲劳分析提供了理论依据。刘佳等人[7]对往复泵运行状态进行了振动测试和关键部件的模态分析,找到了管路系统振动过大的原因,并提出了解决问题的思路。GU Zhen-jie等人[8]基于力平衡原理和质量守恒原理,提出了一种新的往复泵阀动态模型,分析和讨论了管道参数及其交互作用对泵阀动态特性和排量的影响,可为以后往复泵阀的研究提供参考。ZHU G等人[9]利用变刚度弹簧设计了3种新型阀;并采用计算流体力学与动网格技术对模型进行了仿真模拟;结果表明,该新型阀可为提高往复泵性能提供新的研究方向。
上述国内外学者的研究主要是针对传统的摆动泵,而对于全新摆动泵的结构设计方面的研究则相对较少。
针对以上情况,笔者基于虹膜机构可变孔径原理[10-12],设计出一种新的摆动泵结构,以满足用户对液压泵的高要求。
笔者以新型摆动泵为研究对象,基于新型摆动泵结构,推导出虹膜机构位移、速度及相应的瞬时流量方程;同时,利用Fluent软件对新型摆动泵进行数值模拟,分析新型摆动泵工作过程中的压力、速度与流量脉动等分布情况,以期为新型摆动泵的进一步研究工作提供参考。
1 新型摆动泵概述
1.1 摆动泵结构组成
新型摆动泵的结构组成如图1所示。
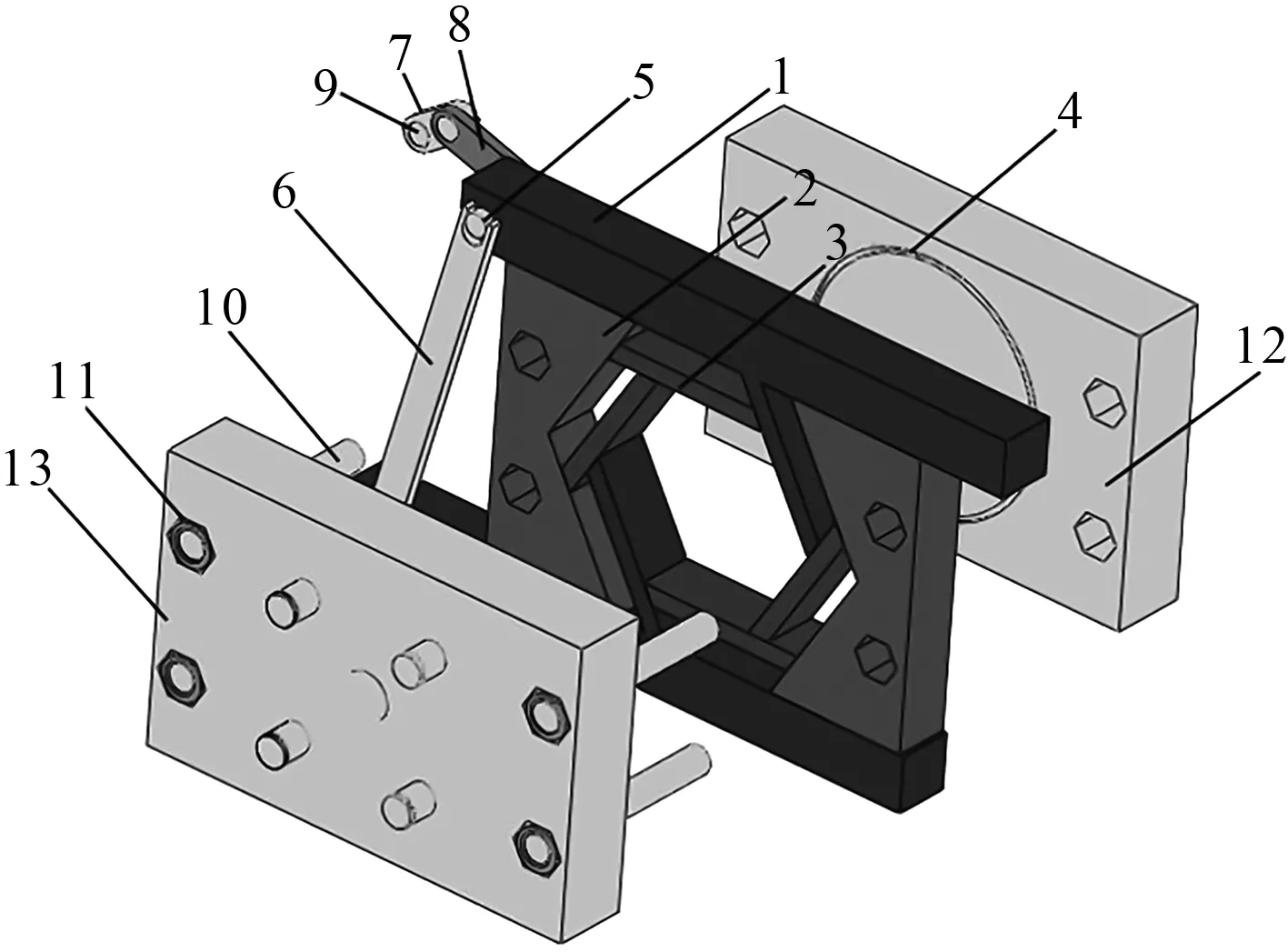
图1 新型容积泵结构图
由图1可知,该泵包含3个单元:1)曲柄连杆传动单元。其由右侧的曲柄、连杆、动力滑块、滑块组成;2)支撑固定单元。其由前泵盖、后泵盖、双头螺栓、六角螺母组成;3)密封单元。其由O型密封圈组成。
其中,动力滑块和滑块构成机械虹膜机构;动力滑块、滑块、前泵盖、后泵盖以及O型密封圈构成密封油腔,是泵的核心部分。
1.2 摆动泵工作原理
新型摆动泵液压回路如图2所示。
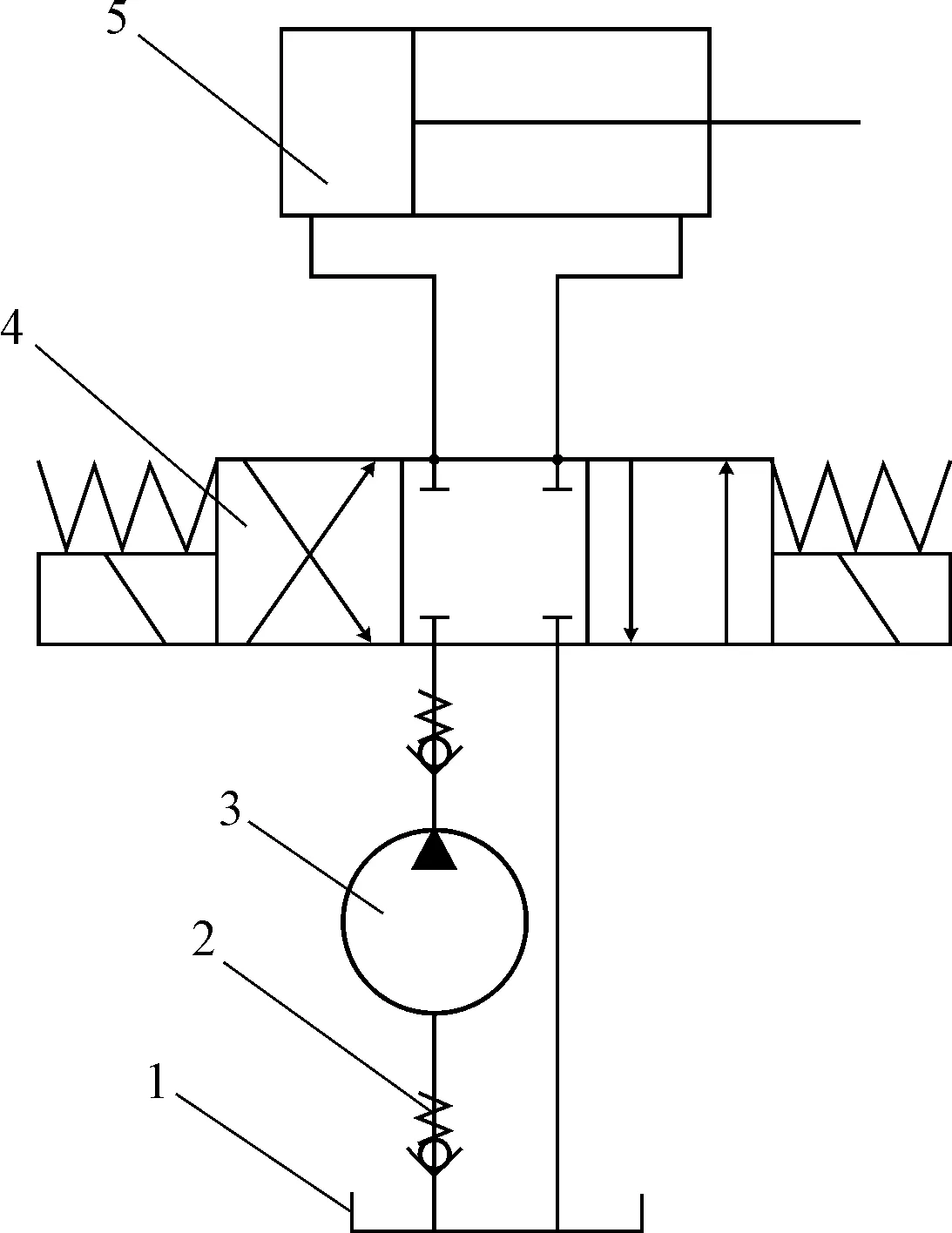
图2 新型摆动泵液压回路
由图2可得:前泵盖与后泵盖分别设有吸油口与出油口,它们各自与吸油通道和排油通道相连;吸油管道和排油管道中分别放置了单向阀,防止吸油管道以及排油管道在工作时油液回流。
新型摆动泵工作原理如图3所示。
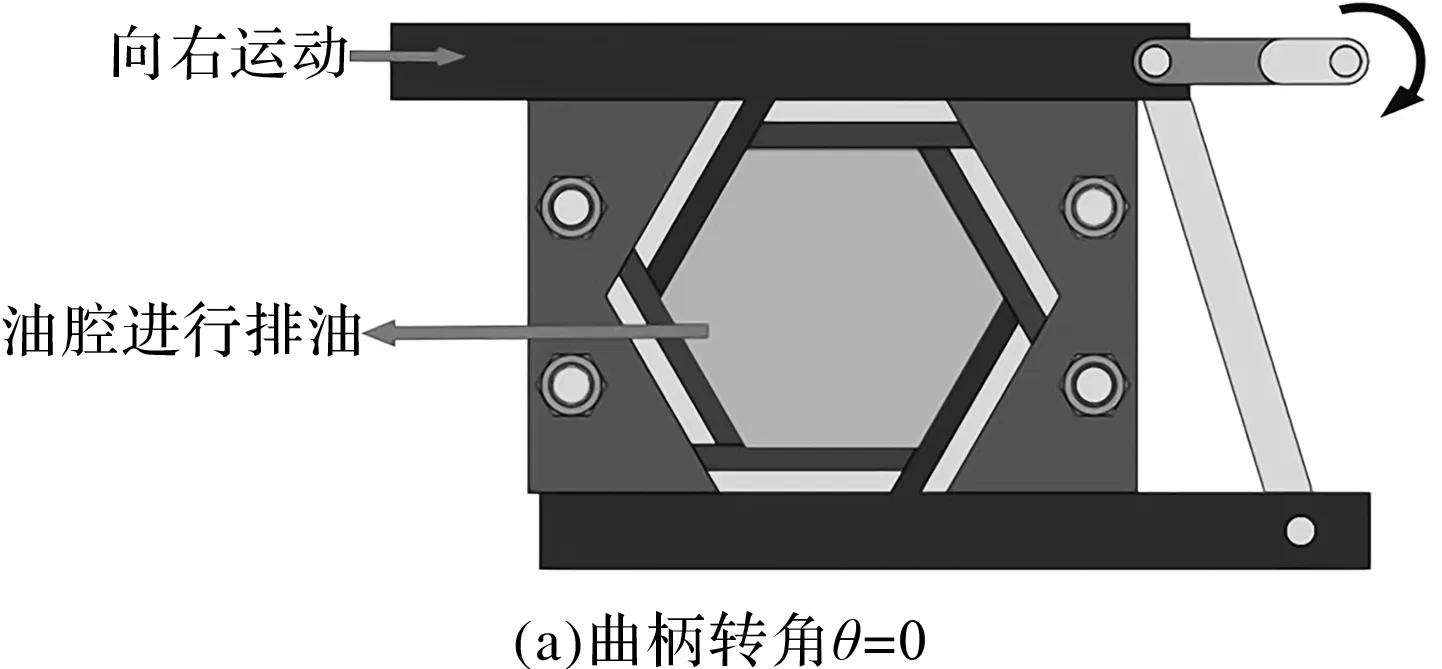
图3 新型摆动泵工作原理图
由图3可得:当动力滑块向左运动时,虹膜机构围成孔径变大,此时油液从前泵盖的吸油管中流入,新型摆动泵完成吸油的过程;同理,当动力滑块向右运动时,虹膜机构围成孔径减小,此时油液从后泵盖的排油管中流出,新型摆动泵完成排油的过程。曲柄和连杆的往复运动使虹膜机构围成的孔径发生周期性变化,新型摆动泵不断吸油和排油,使液压泵可以正常工作。
图3(a)~图3(c)为新型泵吸排油的一个周期内,单向阀的配流方式。
图3(a)~图3(b)过程为:曲柄从0旋转至π,容腔体积减小,由于与吸油口连接的管道中放置了单向阀,故此时油液只从排油口排出,吸油口没有油液进入;当曲柄处于π位置时,油腔处于体积最小状态,排油过程结束。
图3(b)~图3(c)过程为:曲柄从π旋转至2π,容腔体积增大,由于与排油口连接的管道中放置了单向阀,故此时油液只从吸油口吸入,排油口没有油液排出;当曲柄处于2π位置时,油腔处于体积最大状态,吸油过程结束。
2 新型摆动泵运动学分析
新型摆动泵机构运动简图如图4所示。

图4 摆动泵机构运动简图
笔者在图4中建立Oxy坐标系。其中,θ为曲柄转角,正方向如图4所示;L1是曲柄旋转中心与虹膜机构中心在水平方向上的距离;L2是点D与点B在水平方向上的距离。
新型摆动泵关键结构的参数如表1所示。

表1 新型摆动泵关键结构参数
根据虹膜机构可变孔径原理可知:相对于原点,滑块与动力滑块具有相同的位移、速度、加速度方程。
在曲柄滑块运动的基础上,可得虹膜机构在Oxy坐标系下的位移、速度方程,分别为:
(1)
(2)
(3)
式中:ω为曲柄旋转角速度。
笔者根据推导的理论方程,绘制出了虹膜机构的运动学图像,如图5所示。
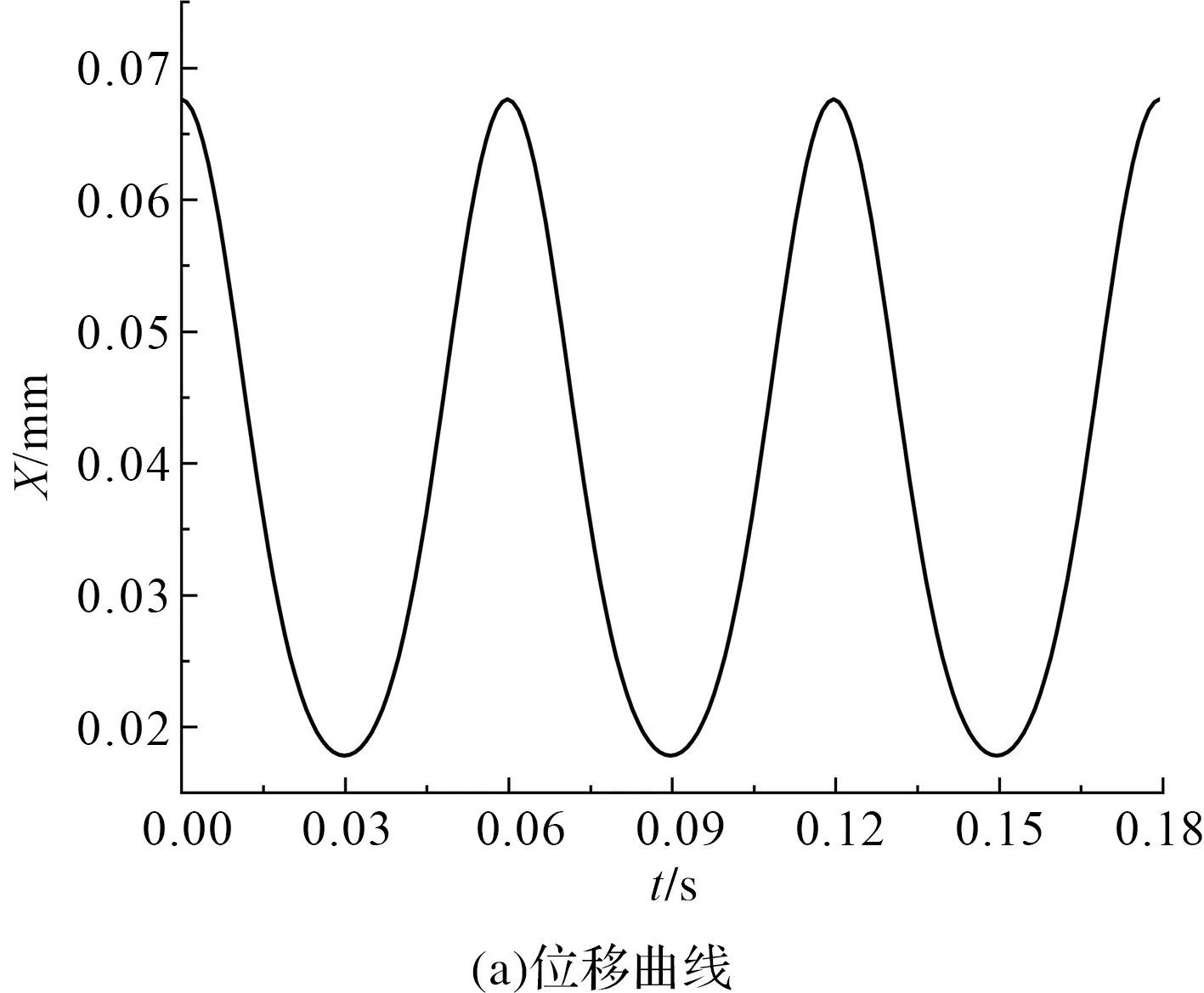
图5 虹膜机构运动学图解
由图5可知:在曲柄的驱动下,动力滑块和滑块构成的虹膜机构做周期性往复式直线运动,使得新型摆动泵可以循环进行吸、排油阶段,在理论上证明了结构设计的有效性。
新型摆动泵工作时,虹膜机构的最大速度为2.938 m/s,最大加速度为206.4 m/s2。
3 新型摆动泵瞬时流量
在不考虑液压介质的可压缩性、虹膜机构的泄漏流量损失的前提下,图4中由于曲柄连杆往复运动产生的理论瞬时流量为:
(4)
其中:负号是指将液压介质流出液压泵工作容腔规定为瞬时流量的正值,而此时对应的液压泵工作容腔体积减小[13]。
按照图4中θ的方向规定为:θ∈[0,π]对应新型容积泵的排液过程,由于吸油管道中设置了单向阀,此时只有出口具有瞬时流量,且Qt为正值;
θ∈[π,2π]对应新型容积泵的吸液过程,由于排油管道中设置了单向阀,此时只有入口具有瞬时流量,且Qt为负值;
笔者重点分析出口理论流量,故有:
(5)
根据式(5)以及虹膜机构位移公式可得:
(6)
式中:a为虹膜机构可变孔径值,在数值上与虹膜机构位移值等值;h为油腔厚度,h=30 mm。
为了提高瞬时流量理论值的精度,笔者根据式(1)、式(2)、式(4)以及式(5),建立了新型摆动泵的Simulink模块。
Simulink模块图如图6所示。
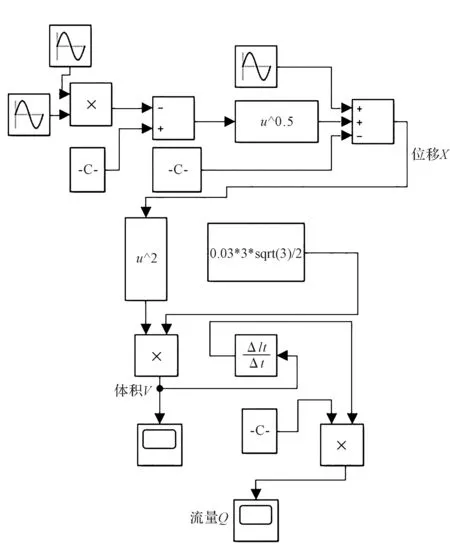
图6 Simulink模块图
模块运行后的数值结果,即理论瞬时流量值—时间曲线,如图7所示。
由图7可知:每个周期内,新型容积泵的最大瞬时流量Qtmax=1 387.2 L/min,最小瞬时流量Qtmin=0。
4 新型摆动泵流场数值模拟
此处笔者所使用的Fluent软件版本为ANSYS Fluent 2020R2。在采用软件进行求解时,先做出以下假设[14]:
1)不考虑摩擦与泄漏;
2)液压油均匀,且不含空气等其他杂质;
3)液压油传送时满足流量连续性条件;
4)忽略温度因素的影响。
4.1 控制方程
1)物理基本守恒定律
新型摆动泵在工作过程中,其内部流场的计算区域会随着流体域边界的运动而不断变化。为此,笔者将采用动网格技术处理流场计算区域的变化过程。
由移动边界∂V所包围的体积守恒方程、质量守恒方程和动量守恒方程分别为[15]:
(7)
(8)
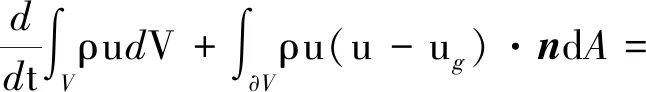
(9)
式中:V为控制体积;∂V为控制体积的边界;u为流体速度;ug为动网格边界的移动速度;n为边界A上外法向单位向量;ρ为液体密度;Su为源项。
2)湍流模型
在进行数值模拟时,笔者选择的湍流模型是RNGk-ε模型。
RNGk-ε模型是在标准模型上做了一些改动后得到的模型。和标准模型相比,RNGk-ε模型改善了旋转效应,提高了解决流体流动问题时的计算精度。
RNGk-ε模型表达式为:

(10)
(11)
式中:Gk为平均速度梯度引起的湍流动能;Gb为由浮力产生的湍流动能;YM为可压缩湍流中波动膨胀对总耗散率的贡献;αk,αε为k和ε有效普朗特数的倒数;Sk,Sε为用户定义的源项。
其中:C1ε=1.42;C2ε=1.68。
4.2 网格划分
为了提高模型的数值模拟精度,笔者选择使用结构化网格单元,对新型摆动泵腔体三维模型进行网格划分;并使用ANSYS中前处理软件ICEM CFD,为腔体的三维模型设置边界条件,生成网格[16]。
其中,笔者设置模型的最大网格单元为0.5 mm,新型摆动泵腔体三维模型划分为122 068个六面体网格,115 008个节点。
模型采用结构化的均匀网格,决定模拟结果是否收敛的主要因素是网格质量,在满足模拟结果精度的条件下,无需增加网格数量。网格质量的评价标准主要是行列式(Determinant 3×3×3)和网格单元的最小角。
为了计算结果的精确性,Determinant 3×3×3参数一般大于0.6;度量网格边之间的夹角范围是0°~90°,0°表示单元退化的网格,90°为完美网格,CFD计算通常要求角度大于30°[17-19]。
其网格的质量图如图8所示。
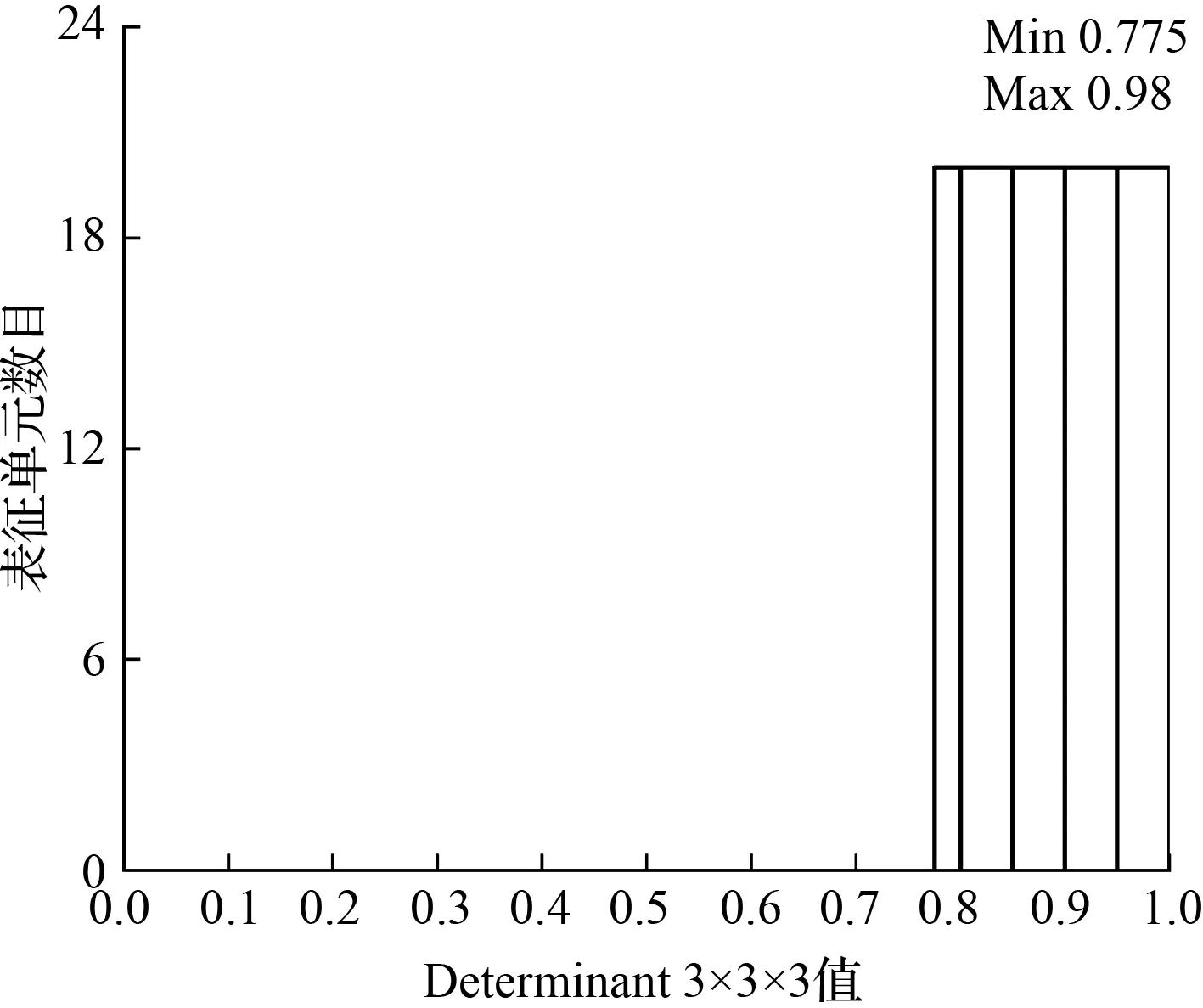
图8 新型摆动泵油腔Determinant 3×3×3值
网格的Angle图如图9所示。
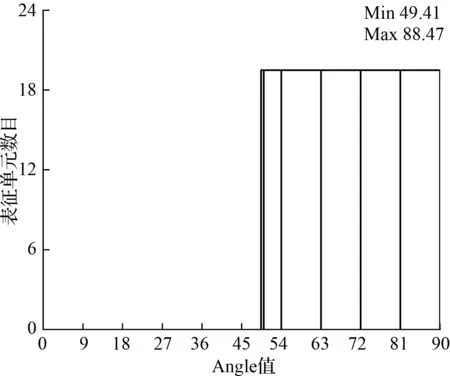
图9 新型摆动泵油腔Angle值
由图8和图9可知:六面体网格的质量为0.775~0.98,介于0.6~1之间;每个网格单元的最小内角Angle的值为49.41°~88.47°,介于30°~90°之间,表明网格质量满足计算要求。
4.3 数值解法
笔者采用Fluent软件进行摆动泵流场的数值模拟。其中,湍流模型设置为RNGk-ε模型,壁面附件采用Standard Wall Functions标准壁面函数。
笔者采用基于压力速度耦合的压力的隐式算子分裂(pressure implicit with splitting of operators,PISO)算法,对新型摆动泵油腔模型进行求解,其他求解器设置均采用默认设置。
其中,时间步长为1×10-4,时步数量为1 200步。
计算过程流程图如图10所示。

图10 计算过程流程图
4.4 边界条件设置及动网格更新
根据新型摆动泵的工况要求,笔者对流体区域(从新型摆动泵的三维模型提取)添加边界条件:
入口类型设置为Pressure-inlet,大小为0 MPa;出口类型设置为Pressure-utlet,大小为20 MPa,其余边界设置为wall。传输介质的计算密度为890 kg/m3,动力粘度为0.023 14 kg/m·s。
由于在工作过程中,新型摆动泵虹膜机构在曲柄连杆的带动下实现了孔径的变化,故将虹膜机构的壁面设置为运动边界,并使用UDF的方式对其进行驱动。
在曲柄连杆的往复运动过程中,吸油腔与排油腔共用一个油腔,单向阀控制着新型摆动泵半个周期排油,半个周期吸油;因此,在数值模拟过程中,为了体现单向阀的功能,进出口的边界是变化的。
在新型摆动泵的一个周期内,其进口边界由原来的压力进口Pressure-inlet转变为wall,再从wall转变为Pressure-inlet;其出口边界由原来的压力出口Pressure-outlet转变为wall,再从wall转变为Pressure-outlet,并在events中进行设置。
笔者采用动态分层法更新动网格(其中,分离因子取0.4,坍塌因子取0.2)。
5 数值计算结果分析
在周期时间0.06 s内,笔者采用数值模拟的方式,得到了新型摆动泵油腔内部的压力、速度等分布云图。
5.1 压力分析
新型摆动泵油腔内部压力云图如图11所示。

图11 新型摆动泵油腔内部压力云图(单位:Pa)
分析图11可得:
在一个周期内,油腔内部压力云图颜色比较明显,压力分布不均匀。在0.01 s~0.03 s内,新型摆动泵处于排油阶段,油腔容积减小,出油口附近形成较大正压,油液从出口排出;最大压力集中在虹膜机构围成的孔径位置,且随着时间的累积,油腔内部最大压力从0.45 MPa降低至0.013 MPa,新型摆动泵也从排油阶段逐渐过渡至吸油阶段。
在0.04 s~0.06 s内,新型摆动泵处于吸油阶段,油腔容积增大,进油口附近形成负压,油液被吸入泵内;最小压力集中在入口位置,且随着时间的累积,入口位置的压力从-0.01 MPa升高至0.075 MPa,新型摆动泵从吸油阶段逐渐过渡至排油阶段。
从图11中可以看出:在t=0.01 s与t=0.02 s、t=0.05 s与t=0.06 s之间,油腔内部压力突变,其原因可能为吸、排油开始时刻,进出口尺寸小,致使油液无法及时排出(需对新型摆动泵模型进行改进,增大进出口尺寸)。
并且,吸油入口处压强低,易产生汽蚀。这是由于供液能力弱,吸入油液时会产生回流(油液入口设计有待研究)。
5.2 速度分析
不同时刻的速度流线图如图12所示。

图12 新型摆动泵油腔内部流场分布(单位:m/s)
新型摆动泵油腔出口与进口平均速度随时间变化曲线,如图13所示。
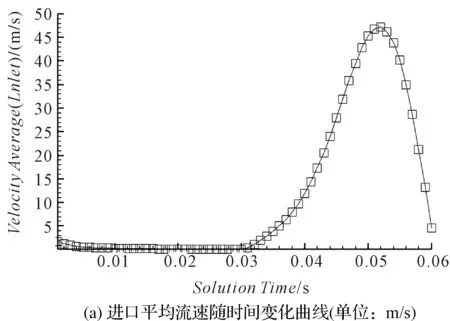
图13 新型摆动泵油腔进出口平均流速
分析图12和图13可得:
在一个周期内,速度矢量的分布较为均匀。最大速度位于进出口处,其最大值为62 m/s,且此时瞬时出口流量和吸入流量达到最大值。在0 s~0.03 s内,新型摆动泵处于排油阶段,故入口位置流速几乎为0;同理,在t=0.03 s后,新型摆动泵开始吸入油液,对应出口处流速几乎为0。
从图12中可以看出:新型摆动泵内流线与速度数值表现出明显的对称性。其中,在排油阶段,出口附近排油通道的油液速度明显高于虹膜机构围成的孔径附近的油液速度;而在吸油阶段,入口附近吸油通道的油液速度明显高于虹膜机构围成的孔径附近的油液速度。
总体上,沿着虹膜机构围成孔径的径向方向,随着与孔径中心间距的增大,油液速度呈现下降的趋势,速度数值分布是合理的,证明虹膜机构的设计是可行的。
5.3 流量脉动
笔者通过数值模拟,得到了新型摆动泵进出口流量的脉动曲线,并将其与理论脉动曲线进行了相互验证。
新型摆动泵进出口瞬时流量对比图如图14所示。

图14 瞬时流量(理论与仿真)对比图
由图14可知:1)瞬时流量的理论值与数值仿真值误差很小,验证了推导的瞬时流量方程与数值仿真过程是正确的;2)进一步确定了虹膜机构的运动学方程是正确的;3)瞬时流量的大小与速度有关,且具有相同的波形。
6 结束语
目前,国内外学者针对摆动泵的研究大多是集中于传统的摆动泵,而对于全新摆动泵的结构设计方面的研究则相对较少。新型摆动泵存在结构复杂和流量脉动大等问题,为此,笔者以基于虹膜机构的新型摆动泵为研究对象,对新型摆动泵进行了运行学分析和数值模拟,得到了虹膜机构的运动学方程,以及新型摆动泵油腔工作周期内的压力、速度云图。
研究结论如下:
1)采用运动学分析可知,该新型摆动泵的周期性和重复性较好,证明新型摆动泵结构设计是有效的;
2)从云图中可以看出,腔体内部最大压力集中在虹膜机构围成的孔径处,且在不同时刻,压力大小是不一样的;在0.01 s、0.04 s等瞬时时刻,腔体流速达到最大值,此时流量瞬时值达到最大,且进出口平均流速曲线与流量脉动曲线具有相同波形;
3)对比流量曲线理论值与数值模拟值,验证了推导的瞬时流量方程与数值仿真过程是正确的;进一步确定了虹膜机构的运动学方程的正确性。
在后续的工作中,笔者将对降低新型摆动泵的流量脉动率做进一步的研究,为以后针对新型摆动泵的流量脉动研究工作打下基础。

