不同参数对塔机吊重摆角和塔身结构振动的影响*
刘 富,杨建伟,2*,谢贻东
(1.北京建筑大学 机电与车辆工程学院,北京 100044;2.北京市建筑安全监测工程技术研究中心,北京 100044)
0 引 言
目前,有许多研究者在静力载荷作用下对塔式起重机(简称塔机)进行了二维特性分析。但是在工程实际中,塔机通常是在耦合运动作用下进行工作的。
很多学者采用有限元方法研究了塔机在不同状态下的结构振动特性。
YANG Zhi-jun等人[1]采用有限元方法对塔机进行了力学分析,并在4种工况下,研究了塔机的稳定性和强度特性;但是,该研究忽略了塔机的动态特性。边晓伟等人[2]利用有限元软件对塔机结构进行了静态分析,在不同载荷共同作用下,得到了塔机的位移云图,也对塔机强度和模态进行了分析;但是,该研究忽略了塔机运动对其强度和模态的影响。邓勇等人[3]利用有限元软件,研究了起重臂仰角大小对塔机抗震性能的影响;但是,该研究忽略了吊重摆角与塔身振动的相互影响。高崇仁等人[4]开发出了一种塔机多工况有限元分析求解器;但是,求解器忽略了吊重摆角的影响。USHIO Y等人[5]提出了一种新的超级计算机静力弹塑性有限元分析方法,采用该方法对端板拉伸螺栓连接处进行了分析,能够设计出精度高、可靠性强的螺栓接头;但是其忽视了塔机动态运动对连接处的影响。KENAN H等人[6]建立了一种有限元模型,该模型能够用于计算结构的固有频率、质量参与因子和模态振型;但是,其没有研究塔臂振动对塔身的影响。张大可等人[7]采用仿真方法,建立了变幅机构的刚体动力学模型,研究了不同参数对吊重摆角的影响;但是,其忽略了塔机结构的弹性影响。崔少杰等人[8]采用有限元方法,研究了静力状态的风载荷对塔机结构在工作和非工作状态下的影响;但是,其没有考虑动力学对塔机的影响。严飞等人[9]采用有限元方法,研究了材料非线性和几何非线性对塔机静态结构的影响;但是,其忽略了吊重摆动角度对塔身振动的影响。
在部分文献中,作者采用解析解的方法,研究了塔机在静动力状态下摆动角度和塔臂振动特性。
HE Wei[10]建立了一种变速度的悬浮载荷系统的平面理论模型;但其忽略了初始角度对塔臂的影响。FENG Run-hui等人[11]建立了单一运动下有效载荷-小车-塔臂的系统动力学方程;但是,其未考虑耦合运动的影响。JIN Liang-hai等人[12]建立了柔性绳在风载作用下的摆动角度系统模型,研究了风荷载对塔机摆角的影响;但是,其忽略了塔身和塔臂振动的影响。兰朋等人[13]采用弹性动力学理论,研究了塔机在回转运动下动态特性;但是,其未考虑耦合运动的动态特性。于兰峰等人[14]采用集中参数法,研究了塔机结构的动力学特性,其建立的模型最大自由度为4;但是,其未把初始角度作为输入参数。董明晓等人[15-17]研究了吊重在变幅运动下的摆动规律,还研究了回转运动对塔臂振动的影响,也研究了不同的吊重和变幅运动对塔臂振动特性的影响;但是,其未考虑塔机加速度对塔机结构的影响。
综上所述,在静力作用下、在单一运动下或者在动力作用下,针对塔机结构振动特性的研究已取得丰硕的成果。但是,上述很多文献把塔机结构当作刚性结构来研究,大量文献也未考虑塔机的加速度对吊重摆角的影响,针对塔机在提升与回转耦合运动下结构振动和空间摆角特性研究的文献则更少。
为了揭示塔机在该提升与回转耦合运动下结构非线性振动的机理,需研究塔身结构非线性振动和吊重的空间摆动在耦合运动下的规律。
因此,针对塔机在提升与回转耦合运动下的结构非线性振动,笔者通过建立塔机从加速到恒速再到减速的动力学模型,研究不同参数对塔身结构非线性振动和吊重摆角的影响。
1 塔机动力学模型
目前,塔机在土木工程领域的应用广泛。塔机的耦合运动在实际工程中比较常见,提升与回转耦合运动对塔机结构非线性振动和吊重摆角的影响比较大。但是为了减少计算量,在工程设计时,一般会将动力问题(采用较大的安全系数)转化为静力问题。该方式会造成结果的不准确。
因此,笔者从动力学角度出发,对塔机在提升与回转耦合运动下的非线性振动进行研究。
1.1 塔机位移关系
随着塔机提升运动的进行,绳长Ly在运动过程中不断变化。各相邻质量之间通过无质量单元连接,各单元存在一定的刚度和阻尼。
非线性运动的塔机结构如图1所示。

图1 塔机模型示意图
根据塔机系统相对坐标和广义坐标之间的关系,可得广义位移与结构参数关系如下:
(1)
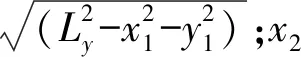
随着塔机从加速到恒速再到减速运行,绳长Ly、角度δ4和角度δ5不断改变。
塔机的减速度和加速度绝对值相等,绳长、平衡臂旋转角度、塔臂旋转角度与时间关系为:
δ5=δ4+π+δ3-δ2
(2)
(3)
(4)
式中:t1为塔机的加速运行结束时刻;t2为恒速运行结束时刻;t3为减速运行结束时刻;L为初始绳长;r为回转齿轮啮合线半径。
假设塔臂为悬臂梁,根据梁挠度理论及受力分析结果,可求出塔臂挠度如下:
(5)

(6)
式中:F为吊重施加在塔臂上的力;E为塔臂的弹性模量;I为塔臂的惯性矩。
1.2 拉格朗日动力学建模
塔机的广义速度、总动能以及总势能分别为:
(7)
(8)
(9)
式中:Xp为质量p在X轴方向上的位移;Yp为质量p在Y轴方向上的位移;Zp为质量p在Z轴方向上的位移;vp为质量p的合速度;αp为质量p扭转角;T为总动能;V为总势能;sp为单元p弹性的伸长量;γp为质量p角度的旋转量;hp为质量p的高度。
根据塔机的几何关系,可推出吊重摆长与摆角的关系如下:
x1=Lysinθ
(10)
y1=Lysinβ
(11)
各个单元的阻尼力和空气阻力为:
(12)
(13)
式中:Qr,pi为质量p的广义坐标i的空气阻力;Qd,i为广义坐标i的阻尼力;c为空气阻力系数;ρp为空气密度;Sp为迎风面积;qi为广义坐标;di为阻尼系数。
基于受力分析,可知广义非保守力如下:
Qi=Qr,pi+Qd,i
(14)
引入拉格朗日动力学表达式如下:
(15)
式中:t为塔机的运行时间;Qi为广义坐标i的非保守广义力。
将式(1)~式(14)代入式(15)中,可推导出结构非线性振动映射关系如下:
(16)
2 实验测试与验证
根据实际塔机结构,笔者首先设计了塔机实验模型结构参数,确定了塔机的材料(Q235);接着选择了角度传感器和采集仪,设计了HWT905传感器布置点,根据设计的尺寸加工了塔机装备,进而安装了实验装备;然后,布置了吊重摆角传感器和连接采集仪,调试了实验塔机和采集仪;最后,进行了实验测试。
2.1 实验步骤与参数
实验人员操作塔机,使其进行提升与回转耦合运动,并进行摆角数据采集。每次塔机运行都是从加速到恒速再到减速。在实验测试时,笔者选择3个不同的吊重进行实验,每个条件下重复3次,最后取平均值。
笔者设计的实验塔机结构参数值如表1所示。
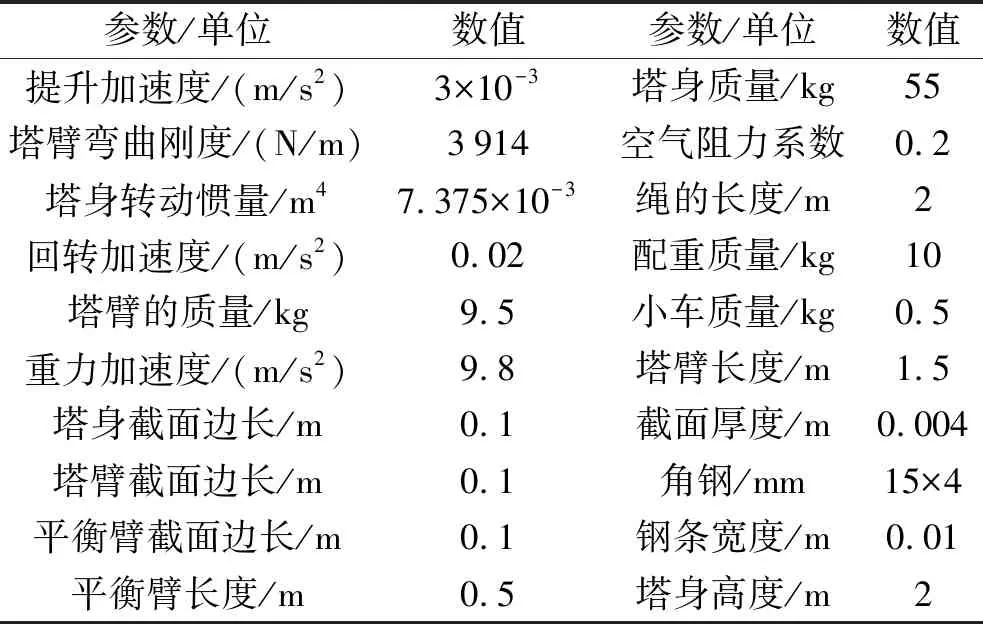
表1 塔机设备结构参数
测试设备布置如图2所示。

图2 实验的设备
2.2 实验与仿真结果对比
实验结果与仿真结果的对比情况,如图3所示。

图3 实验结果与仿真结果对比
从图3可以看出:在加速和减速阶段,仿真结果与实验结果有一定的差距,两者在恒速阶段差距比较小,仿真与实验的结果整体变化趋势一致。
因此,上述非线性塔机模型能呈现塔机真实的振动特性。
3 非线性动态响应和分析
基于已建立的塔机动力学模型,笔者研究不同参数对塔机吊重摆角和塔身振动的影响。
3.1 不同参数对吊重摆角振动的影响
3.1.1 改变提升加速度
改变提升加速度对吊重摆角的影响如图4所示。

图4 不同提升加速度对吊重摆角的影响
从图4(a)可以看出:随着时间的增加,角θ先增加后减小。在恒速末期时,摆角θ存在最大值;在加速度阶段,摆角θ变化不明显。当提升加速度为0.01 m/s2时,摆角θ存在最小值;当提升加速度不大于0.007 m/s2时,摆角θ较大。
从图4(b)可以看出:摆角β在减速阶段存在最大值。随着提升加速度的增加,当提升加速度为0.007 m/s2时,摆角β存在最大值。提升加速度在塔机加速运行阶段对摆角β无明显影响;在恒速和减速阶段对摆角β有一定影响。
由此可见,提升加速度对θ角的影响比β角大。
3.1.2 改变回转加速度
改变回转加速度对吊重摆角的影响如图5所示。

图5 不同回转加速度对吊重摆角的影响
从图5(a)可以看出:在恒速阶段,随着时间的增加,角θ的振幅有最大值;在加速阶段,振幅有最小值。随着回转加速度的增加,角θ的振幅逐渐增大,角θ的振动周期几乎不变。
从图5(b)可以看出:随着回转加速度的增加,角β的振动周期逐渐减小。当回转加速度为0.07 m/s2时,摆角β存在最大值。
因此,回转加速度对角θ的振幅影响比角β的振幅大。
3.1.3 改变β0角
改变β0角对吊重摆角的影响如图6所示。
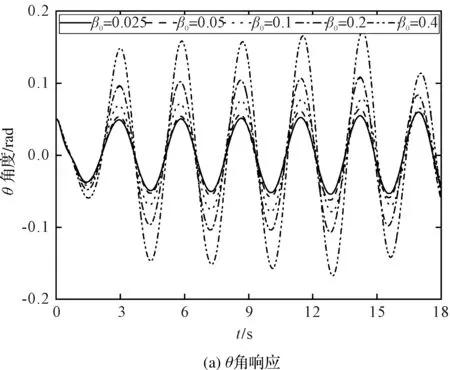
图6 不同β0对吊重摆角的影响
从图6(a)可以看出:随着初始角度β0的增加,角θ的振幅不断增大,但是振动周期不变。随着时间的增加,不同的角β0在加速和恒速阶段对角θ的振幅差距存在不同程度的影响;在减速阶段,对角θ的振幅差距影响变小。
从图6(b)可以看出:随着初始角度β0的增加,角β的振幅明显增大,但是振动周期没有显著变化。在加速和恒速阶段,随着时间增加,不同的角β0对角β的振幅差距存在一定程度的影响。初始角度β0对空间摆角的振幅存在较大的影响。
因此,初始角度β0对角β的振幅影响比角θ的振幅大。
改变θ0角对吊重摆角的影响如图7所示。
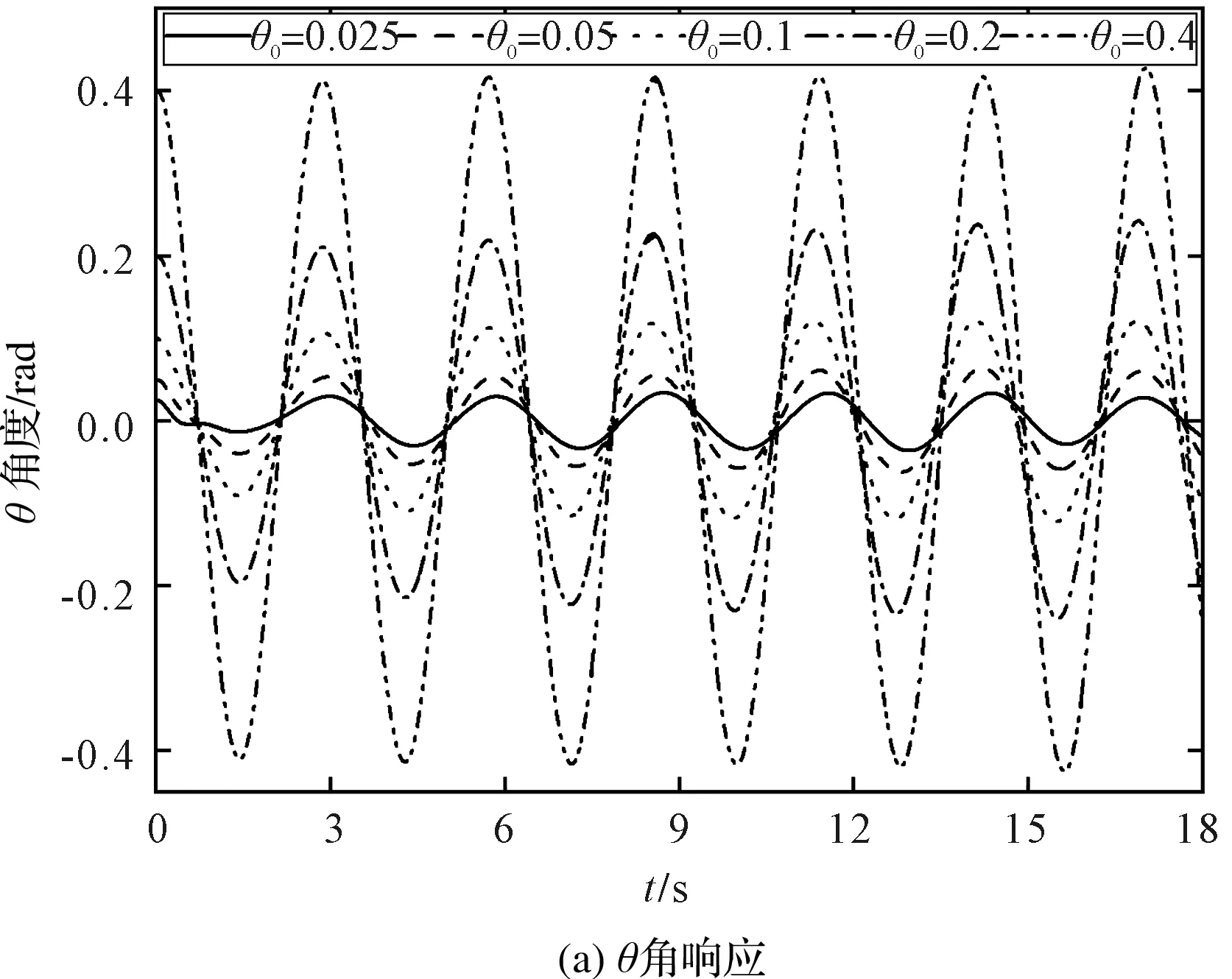
图7 不同θ0对吊重摆角的影响
从图7(a)可以看出:随着初始角度θ0的增加,角θ的振幅显著增加,但是振动周期没有明显变化。在恒速末期时,角θ的振幅存在最大值。随着时间的增加,改变的初始角度θ0对角θ振幅的差距影响比较稳定。
从图7(b)可以看出:随着初始角度θ0的增加,角β振动周期逐渐减小。当初始角度θ0不大于0.4 rad时,随着角度θ0增加,角β的振幅逐渐减小。当角θ0为0.4 rad时,角β的振幅明显增大;振幅在恒速阶段有发散趋势。
由此可见,初始角度θ0对角θ的振幅影响比角β的振幅大。
3.2 不同参数对塔身结构振动的影响
通过对塔机动力学模型的分析,笔者发现不同的提升加速度对塔身结构振动的影响很小。
3.2.1 改变回转加速度
改变回转加速度对塔身振动的影响如图8所示。

图8 不同回转加速度对塔身振动的影响
从图8(a)可以看出:随着回转加速度的增加,塔身振动周期在x轴方向上逐渐减小;塔身振幅在加速阶段存在最大值;
从图8(b)可以看出:随着回转加速度的增加,塔身振动周期在y轴方向上逐渐减小。当回转加速度为0.07 m/s2时,塔身的振幅在y轴方向上有最大值。当回转加速度不大于0.01 m/s2时,塔身的振幅沿x轴和y轴方向较小。
因此,回转加速度在恒速和减速阶段对塔身振动影响较大。
3.2.2 改变β0角
改变β0角对塔身振动的影响如图9所示。

图9 不同β0对塔身振动的影响
从图9(a)可以看出:随着初始角度β0的增加,塔身x4在减速与恒速阶段周期和幅值均增加。当初始角度β0不小于0.4 rad时,塔身振幅在加速阶段沿x轴方向减小。
从图9(b)可以看出:随着初始角度β0的增加,塔身振幅沿y轴方向增加;沿y轴方向在恒速阶段比在加速和减速阶段增加量大。当初始角度β0不小于0.2 rad时,塔身振幅在加速和恒速阶段沿y轴方向波动较大。
因此,初始角度β0在y轴方向上的影响比在x轴方向上大。
3.2.3 改变θ0角
改变θ0角对塔身振动的影响如图10所示。
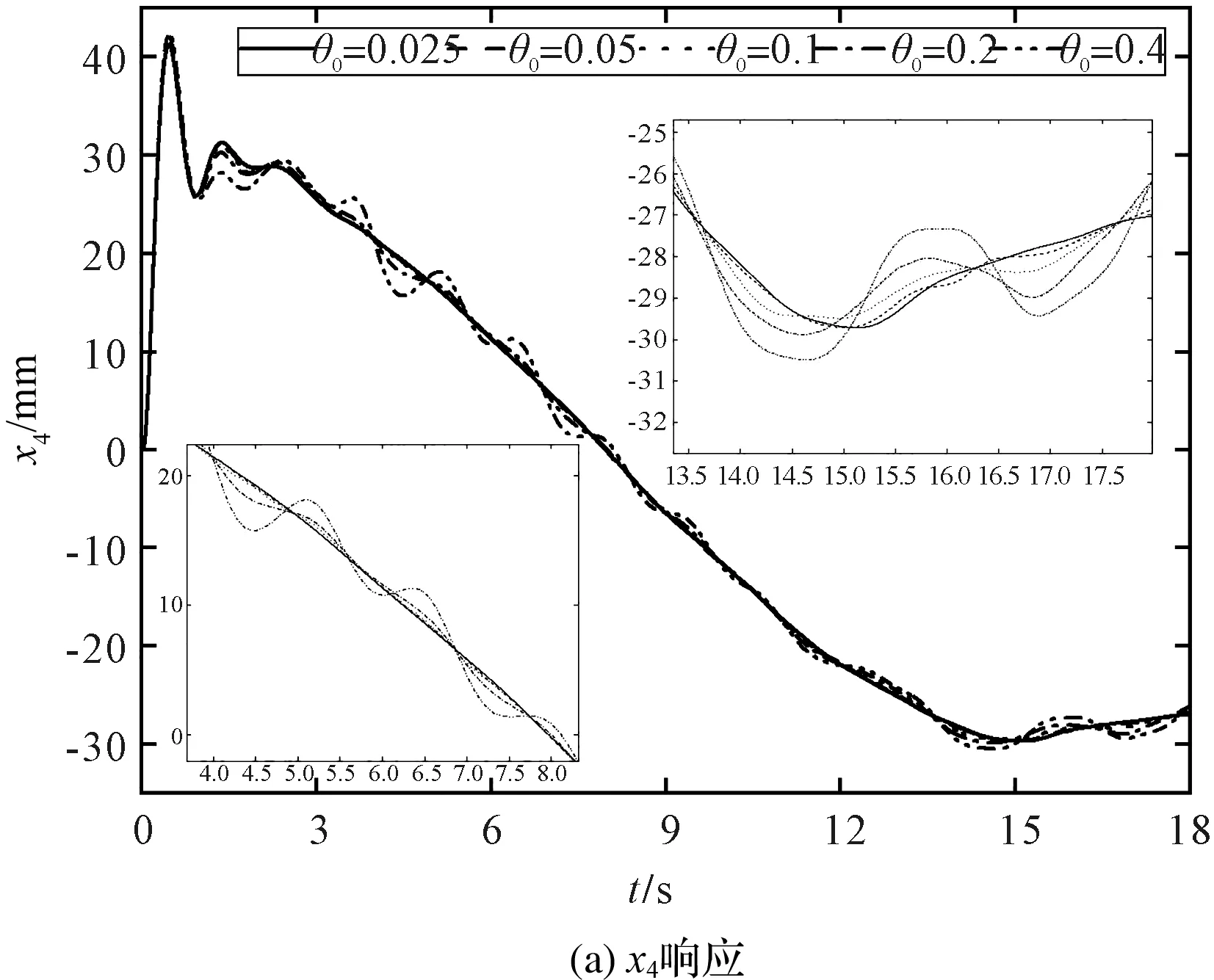
图10 不同θ0对塔身振动的影响
从图10(a)可以看出:随着初始角度θ0的增加,塔身的振幅和周期沿x轴方向增大。当θ0角不小于0.2 rad时,塔身x4的振幅在加速阶段增加不显著;x4的振幅在恒速和减速阶段波动较大;
从图10(b)可以看出:随着初始角度θ0的增加,塔身的振幅和周期沿y轴方向增大。当θ0角不小于0.2 rad时,塔身y4的振幅在加速阶段变化不明显;y4的振幅在恒速和减速阶段波动较大。
因此,初始角度θ0在x轴方向上的影响比在y轴方向上大。
4 结束语
针对塔身振动和吊重摆角在提升与回转耦合运动下的变化规律进行了研究,笔者进一步研究了塔机从加速到恒速再到减速的运行规律。通过改变提升加速度、回转加速度和初始角度的数值,对塔机结构非线性振动进行了研究;探讨了不同参数对塔身结构振动和吊重摆角的影响。
研究结论如下:
1)提升加速度对角θ振幅的影响比角β振幅大;选择较大的提升加速度对摆角和塔身振动影响较小;
2)回转加速度对吊重摆角振动周期和幅值的影响较大。回转加速度对角θ振幅的影响比角β振幅较大;选择合适的回转加速度能减小摆角振幅和周期;
3)回转加速度对塔身结构振动周期和幅值的影响较大。选择较小的回转加速度能降低塔身结构振幅;
4)初始角度对吊重摆角的振幅有明显影响。当改变初始角度的方向与吊重摆角方向一致时,吊重摆角在该方向上受到较大影响;
5)当初始角度小于0.2 rad时,初始角度对塔身结构振动影响较小。
在后续的工作中,笔者将从疲劳角度出发,研究不同的结构参数对塔机关键位置的疲劳累积影响。

