基于理解的初中数学逆向教学设计
——以“圆和扇形”单元为例
王生义
(江苏省连云港市墩尚中学,江苏 连云港 222100)
逆向教学设计以理解为目的,通过从学习目标和关键理解要点开始,选择合适的评估证据并设计学习体验和活动,帮助学生深入理解知识[1].本文以人教版七年级上册第三章《圆和扇形》单元为例,将基于理解的逆向教学设计的三个阶段相互关联,构成一个循环的教学过程.这种教学方法注重学生的主动学习和深层次的理解,培养学生的批判性思维和问题解决能力,从而提高学习的质量和效果.
1 基于理解的逆向教学设计
基于理解的逆向教学设计这个观点首次由威金斯和麦克泰格在《追求理解的教学设计》这本书提出[2].该教学设计颠覆了传统的教学方式,以学生理解为先,教师在开始新的学习周期时,需要明确学习结果并确定评估证据,然后设计学习体验和教学活动,并通过评估证据来检验学生的学习成果.它强调学生可以理解哪些知识、学习到什么知识、可以实现怎样的学习目标、怎样的方式可以较好地实现预期的目标,从而培养学生的自主学习和问题解决能力[3].具体分为以下三阶段.
1.1 明确教学目标
教师需要明确期望学生在学习过程中达到的目标和预期结果,这可以是特定的知识点、技能或能力.明确的学习结果有助于为学生提供明确的学习方向和目标,同时也可以更好地调整和个性化教学,并为后续的评估和教学活动提供指导.当然,这个学习结果需要先了解学生的学习情况,考虑学生的背景、兴趣、学习风格和能力水平,确保学习结果与学生的需求和发展阶段相匹配,进而确定学生学习内容的先后次序如下图1所示.
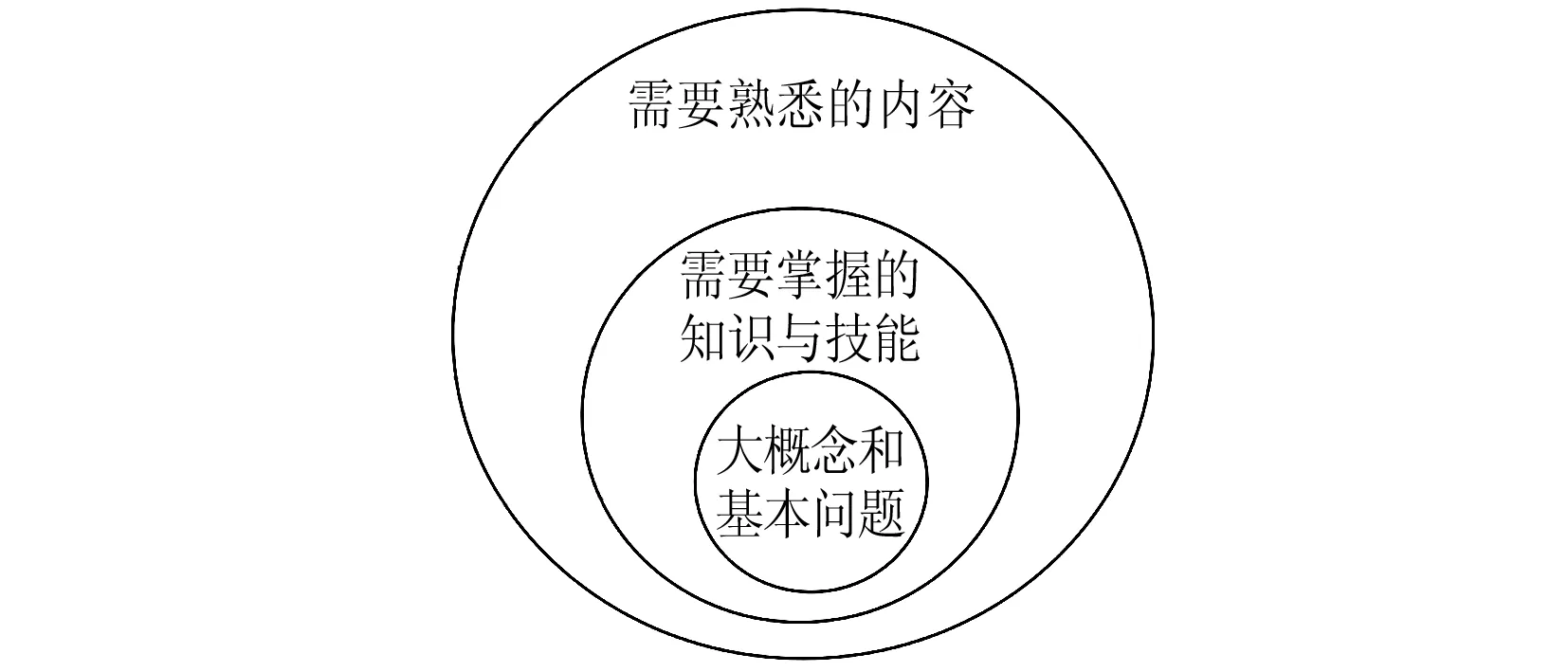
图1 学生学习内容的先后次序
1.2 确定评估学生的证据,即教学评估
在这个阶段,教师需要确定合适的评估方式和评估证据,以判断学生是否达到了预期的学习结果.评估证据可以是学生的作品、项目成果、考试成绩、口头表达等,确保评价方式与学习目标的要求相匹配如图2为两者的关系,并考虑学生的多样性和不同的学习方式,保证评价标准具有可衡量性和可操作性,能为学生提供有意义的指导.同时,选择合适的评估方式和证据可以帮助教师准确地评估学生的学习成果,并为教学提供反馈和调整的依据.
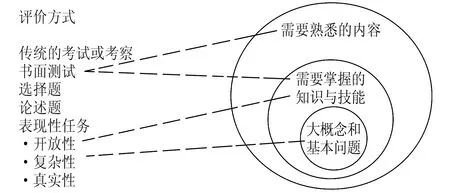
图2 教学目标与评估方法的关系

图3 圆相关的实物或模型
1.3 设计教学活动和学习活动
教师需要设计学生的学习体验和授课活动,以促进学生达到预期的学习结果.通过选择适当的教学策略、准备多样化的学习资源、设计有挑战性的学习任务、创造互动与合作的学习环境,如小组讨论、实践活动、案例研究等,并关注个性化的学习需求,以激发学生的学习动力,培养他们的批判性思维和创造性解决问题的能力.这样的设计将使学习变得有趣、有意义,并帮助学生在学习中取得更好的成果.
2 基于理解的逆向教学设计案例
2.1 阶段一
2.1.1课程单元教学目标
(1)准确地定义和描述圆的基本概念,以及解释圆的性质.
(2)正确地计算扇形的面积和弧长,并能够合理地应用所学知识解决实际问题.
(3)清晰地表达数学思想和解题过程,并用准确的数学语言和符号论证和计算.
2.1.2学生的学习标准
(1)定义和描述圆的圆心、半径、直径、弧长等基本概念.例如,学生能够正确定义圆心为位于圆内,到圆上任意一点距离相等的点.
(2)说明圆的圆心角等于弧度角、同弧度的圆心角相等、圆内角和等于180度等性质.例如,学生能够理解圆心角是以圆心为顶点的角,其度数等于对应的弧度.
(3)计算扇形的面积和弧长,理解扇形面积和弧长的计算公式的推导过程.例如,学生能够应用面积计算公式S=1/2r2θ以及弧长计算公式L=rθ进行计算.
何守一“是是是”的直点头,等权头辛燕晓一走,何守一和郑玉英就逼问何东到底为什么没登记,何东说不想,再问为什么,就说不出来了,因为怎么看何东都不觉得现在是阐述自己理想的时候,结果父母意见就是,赶紧结了,别折腾了。
(4)将所学知识应用于解决实际问题,如计算圆形花坛的面积、扇形的面积等.例如,学生能够应用所学知识计算一个半径为5 cm的扇形所覆盖的面积.
(5)应用圆与扇形相关的公式对不规则形状或者组合图形的周长和面积进行计算.
2.1.3实际应用
(1)应用所学的圆和扇形的知识解决实际问题.例如,学生可以计算圆形花坛的面积,以确定需要的土壤和植物的数量.
(2)应用扇形面积和弧长的计算方法,来解决与地理、建筑等领域相关的问题.例如,学生可以计算一个舞台上的扇形区域的面积,以决定舞台上的舞蹈表演区域.
(3)将圆和扇形的概念应用于日常生活中的实际情境.例如,在选购蛋糕时,学生可以计算扇形蛋糕的面积和价格,以做出更明智的选择.
2.2 阶段二
在人教版《圆和扇形》单元中,为了评估学生对于所学知识的掌握程度,可以采用以下合适的评估证据:
2.2.1笔试评估
(2)设计解答题,要求学生回答文字题目,解决与圆与扇形相关的问题.例如,要求学生计算不规则形状或组合图形的周长和面积,并给出解题步骤和思路.
2.2.2实际问题解决评估
(1)给学生一些实际情境,要求他们运用圆与扇形的知识解决问题,例如计算花坛的面积、舞台上扇形区域的面积等.
(2)要求学生给出解决问题的全面解答,包括问题的分析和解决思路,并通过计算和推理得出结论.
2.2.3实际操作评估
(1)通过测量、模拟实验等,进行圆与扇形面积、周长以及相关公式的推导进行验证.
(2)组织学生进行小组或个人项目作业,要求他们设计和绘制一个具有特定要求的不规则形状或组合图形,计算其周长和面积,请说明设计意图.
(3)要求学生书面报告项目作业的过程和结果,并附上必要的图表和计算步骤.
2.3 阶段三
以下为有利于学生理解的具体活动.
2.3.1演示与探究
(1)首先使用实物或模型,展示圆的形状和特性,例如使用井盖、圆盘、圆规等,引导学生观察和描述圆的性质.
(2)设计探究活动,让学生自己测量和验证圆心角、弧长等与圆相关的性质.例如,组织学生测量不同角度的圆心角,并观察角度与弧长的关系.
2.3.2问题解决与实践
(1)提供一系列与圆和扇形相关的问题,鼓励学生运用所学知识解决.例如,给学生几个不规则形状的图形,要求他们计算每个图形的面积和周长.
(2)设计实践活动,让学生在实际场景中应用圆与扇形的知识.例如,带学生到校园中测量不同树木的树冠直径,并计算树冠的面积.
2.3.3合作学习与讨论
(1)安排学生成小组,让他们共同讨论和解决与圆与扇形单元相关的问题.通过讨论,促进学生思维的碰撞和深入理解.
(2)设计小组项目,要求学生合作设计一个花坛或场地的规划,包括圆形和扇形区域的设计和计算.
2.3.4利用技术工具
引入相关的数学教学软件或在线工具,让学生通过模拟和计算来探索圆与扇形单元的知识.例如,使用几何绘图软件进行不规则图形的绘制和计算.
2.3.5视频和多媒体资源
利用相关的视频和多媒体资源,呈现圆与扇形单元的概念和应用.通过视听的方式,帮助学生更直观地理解和记忆相关知识.
3 小结与启示
基于理解的逆向教学设计在初中数学教学中,有效提升学生的理解和应用能力.通过明确学习目标和理解要点,引导学生参与观察、探索、实践和问题解决,促进知识建构,并整合数学和实际情境,设计实用的活动培养深度理解,创造多样化的学习体验,以激发学生学习兴趣.同时,及时反馈和评估,巩固知识和调整教学策略.进而,做到以学促教、以理解为先的教学和学习,促进深层次的学习,为学生未来的学习打下坚实的基础.
———《扇形的认识》教学廖

