用解析法求正方形背景下线段(之和)的最值

徐 岚

(苏州市第十六中学校, 江苏 苏州 215003)

正方形是一种特殊的四边形,在角和边等方面具有多重性质,便于旋转形成线段的最值,因而成为命题热点.而求解最值往往有多种模型,有没有一种模型可以解决大部分关于正方形背景的求解线段最值呢?有,那就是直角坐标系模型.

1 常见题型

1.1 “一定一动”基本型

例1 如图1,正方形ABCD中,边长为4,E是BC边上一个动点,连结AE,过E作EF⊥AE交DC于F,求AF的最小值.

图1 例1(a)图 图2 例1(b)图

分析图1中,求AF最小值,A是定点,F是动点,组成“一定一动”最值题的基本类型.解题关键抓住EF⊥AE这个条件,结合正方形相关性质,构造全等三角形或相似三角形,得到相应线段比值关系.在此基础上,建立坐标系,设点的坐标,利用两点距离公式求值.

解答如图2,∵四边形ABCD是正方形,EF⊥AE

∴Rt△ABE∽Rt△ECF(一线三直角).

要AF为最小值时,则a=2,代入原式,解得AFmin=5.

1.2 “两定一动”引申型

例2 如图3,正方形ABCD中,E是BC边上一动点,△AEP为等腰直角三角形,若AB为4,则PA+PD的最小值是多少?

图3 例2(a)图 图4 例2(b)图

分析图3中,求PA+PD的最小值是多少,属于“两定一动”类型,显然是例1基础上引申而来.由“两定一动”自然想到将军饮马模型,而P点运动轨迹是什么呢?因为P是随E点而动,而且,点P、E都绕A点运动,它们比值是定值,夹角∠PAE也是定角,符合瓜豆原理,所以,P点运动轨迹也是一条直线.据此分析,根据瓜豆原理和将军饮马模型可以求得线段和的最小值.用直角坐标系模型更为简便[1].思路和方法与例1同理.

解如图4,过P点作PF⊥BC,

∵△AEP为等腰直角三角形,∴Rt△ABE≌Rt△EFP,

则AB=EF=4,BE=PF.设BE=a,

则PF=a,BF=4+a.

在直角坐标系中,有A(0,4),D(4,4),P(4+a,a).

设P(a,0),A(0,4),D(2,-2),如图5.

图5 例2(c)图

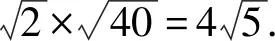
反思此题需要以数解形,简化解题思维;又需要以形解数,简化计算.数形结合,灵活运用,思维含量极高.

1.3 “双动点”提高型

例3 如图6,正方形ABCD边长为4,E为BC上的动点,连结AE,DE.将AE绕点E顺时针旋转90°得到线段EF,G为DE中点,连结FG,求FG的最小值.

图6 例3(a)图 图7 例3(b)图

分析图6中,F、G都是动点,对于双动点,第一步,考虑将其转化为“一动一定”,此题可以延长EF至H使EF=FH,连结DH,则DH=2GF,而D是定点.第二步,求出动点H的轨迹,应该是一条直线,然后根据点到直线的距离求出最小值.如果用坐标系模型,解题思路更简洁.

解答 过F作FP⊥BC延长线交于P点,如图7,

∵AE=EF,∠AEF=90°,

∴Rt△ABE≌Rt△EPF,

则AB=PE,BE=PF.设BE=2a,

则E(2a,0),D(4,4),F(4+2a,2a),G(a+2,2),

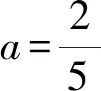
1.4 “多动点”拓展型

例4 如图8,正方形ABCD边长为4,E为BC上的动点,连结AE,DE.将AE绕点E顺时针旋转90°得到线段EF,G为DE中点,H为AE中点,连结FG,FH,求FG+FH的最小值.

图8 例4(a)图 图9 例4(b)图

分析图8中,F,G,H都是动点,FG、FH又是动线段,属于多动点类型,难度较大.先考虑把动线段转化为“一定一动”的线段,可以延长EF至P使EF=PF,连结PA、PD,则FG+FH就是PA+PD的一半,变成“两定一动”类型.下面同例2.如果用坐标法,思路简洁.

解答:过F点作PF⊥BC交BC延长线于P,如图9,则Rt△ABE≌Rt△EPF,有BE=PF,AB=EP,设BE=a,则有F(4+a,a),

下面解答同例2,略

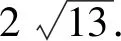
2 模型思考

数学教学的主要目标是帮助学生学会思考,用思维方法的分析带动具体知识的学习,才能提高学生的解题能力.既要学会一题多解的发散思维,也要训练多题一解的集中思维,在解题过程中,学生要不断地感悟和理解抽象、推理、直观的作用,得到新的数学模型,改进思维品质,扩大应用范围,提升关键能力[2].通过一个问题解决一类问题,达到认识问题的本质,提升数学素养.

运用坐标模型解决正方形背景下多种类型的最值问题,有两点思考.

2.1 适用的题目条件

首先,正方形背景.因为正方形在边,角,对角线等多方面有特殊的性质,易于建立直角坐标系,正方形顶点和对角线交点坐标容易建立,为解题带来了诸多的便捷.其次,要有动点线段90度旋转.因为这个条件结合正方形性质可以构造“一线三直角”模型,得到两直角三角形相似或全等,求出对应边的数量关系,便于求出关键点的坐标值.最后,动点运动轨迹为直线,一般不适用于圆的轨迹,因为圆轨迹上的点坐标建立比较复杂.

2.2 解题思路归一

学习要遵循循序渐进原则,透彻理解基本题型的解题思路及原理.所以要让学生对“一定一动”基本型搞清搞透.首先,利用“一线三直角”模型,应用全等三角形模型或相似三角形模型,求出对应边数量关系,得出关键点的坐标值[3];如图1中,求出F点坐标;其次,根据坐标系中两点坐标,代入两点距离公式;最后,根据函数公式等求出最值.

总之,各种问题都有这个内在规律和联系,只要我们善于探究发现规律,探究多题一解的规律,我们的思维品质才会提升,要善于分析、归纳、总结,解题思维水平一定得到极大提高.