多解多变 精彩呈现——以2023年高考全国乙卷文科第11题为例

李 寒

(贵州省贵阳市第一中学,贵州 贵阳 550081)

2023年高考乙卷文科的第11题设问表达清晰、简洁,情境熟络,给人以“似曾相识”的亲和感,是一道能够很好地体现“基础性”和“全面性”考查要求的高考试题[1].

1 试题再现

题目已知实数x,y满足x2+y2-4x-2y-4=0,则x-y的最大值是( ).

2 一题多解

分析1设x-y=μ,与已知条件中的二元二次方程联立,消去x,运用判别式法解答.

解法1设x-y=μ,则x=y+μ.

2y2+(2μ-6)y+μ2-4μ-4=0.

因为y∈R,则判别式△=(2μ-6)2-4×2(μ2-4μ-4)≥0.

化简,得μ2-2μ-17≤0.

故选C.

点评解法1运用“判别式法”解答,是这类问题“通性通法”之一.

分析2将已知条件中的二元二次方程配方为(x-2)2+(y-1)2=9,运用三角换元法求解.

解法2将x2+y2-4x-2y-4=0,

配方、整理,得

(x-2)2+(y-1)2=9.

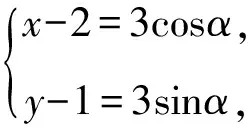
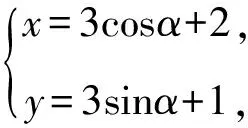
所以x-y=3cosα+2-3sinα-1

=3(cosα-sinα)+1

因为α∈[0,2π],

故选C.

点评解法2运用三角换元,把代数式的最值问题转化为三角问题,应用三角恒等变换和三角函数的有界性解答,也是解这类问题的一种常用解答方法之一.

分析3将已知条件中的二元二次方程配方、整理为(x-2)2+(y-1)2=9,设x-y=μ,利用圆心到直线的距离小于等于半径求解.

解法3由x2+y2-4x-2y-4=0,

配方、整理,得

(x-2)2+(y-1)2=9.

设x-y=μ,则圆心到直线x-y=μ的距离

故选C.

点评解法3运用“几何法”解答,简化了运算求解过程,是最为常用的“通性通法”.

分析4将已知条件中的二元二次方程配方、整理为(x-2)2+(y-1)2=9,设x-y=μ,即y=x-μ,此时“-μ”是直线y=x+(-μ)在y轴上的截距.如图1,平移直线y=x至与圆在右下方相切时,直线y=x+(-μ)在y轴上的截距最小,μ最大,利用圆心到直线的距离等于半径解答.

解法4由x2+y2-4x-2y-4=0,

配方、整理,得

(x-2)2+(y-1)2=9.

设x-y=μ,如图1,平移直线y=x,当平移至与圆相切时,则圆心到直线x-y=μ的距离

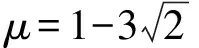
故选C.

图1 解法4示意图

点评解法4通过平移直线,数形结合解答,快速简捷,可谓是一种“秒杀”该试题的一种解法!

分析5 将已知条件中的二元二次方程配方、整理为(x-2)2+(y-1)2=9,进行双变量换元,然后应用重要不等式“x2+y2≥2xy,当且仅当x=y时取到等号”的变形“2(x2+y2)≥(x+y)2”进行解答.

解法5由x2+y2-4x-2y-4=0,

配方、整理,得

(x-2)2+(y-1)2=9.

m2+n2=9,x-y=m-n+1.

因为2(m2+n2)≥(m+n)2,

所以(m-n)2=[m+(-n)]2

≤2[m2+(-n)2]

=2(m2+n2)=18.

当且仅当m=-n,即

点评解法5首先双变量换元,然后运用重要不等式的变形式解答,思维别致、颇具新意.

解法6由x2+y2-4x-2y-4=0,

配方、整理,得

(x-2)2+(y-1)2=9.

由二维柯西不等式,得

[(x-2)2+(1-y)2]·(12+12)≥[(x-2)·1+(1-y)·1]2=(x-y-1)2.

所以(x-y-1)2≤9×2=18.

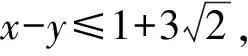
点评解法6依据已知条件中方程左边配方后为平方和的结构特点,配凑后应用二维柯西不等式来解答,十分巧妙.

解法7由x2+y2-4x-2y-4=0,

配方、整理,得

(x-2)2+(y-1)2=9.

由二维权方和不等式,得

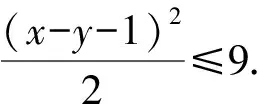
所以(x-y-1)2≤18.

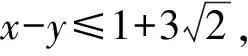
点评解法7依据已知条件方程中左边配方后为平方和的结构特点,在进行配凑变换的基础上,变换出二维权方和不等式左边的形式,应用二维权方和不等式解答.

3 一题多变

题设条件中的方程是圆的一般方程,而涉及与圆有关的最值问题主要有以下三类,常用方法是借助图形性质,利用几何法,数形结合求解.

(2)截距型.形如t=ax+by形式的最值问题,可转化为动直线截距的最值问题.

(3)距离型.形如(x-a)2+(y-b)2的最值问题,可转化为动点到定点距离的最值问题.

以下从这三个方面,如果不改变已知条件中的方程,只改变结论中的目标式,可有:

令P(x,y),A(-3,-2),点P在圆(x-2)2+(y-1)2=9上运动.

设过点A的直线l的方程为y+2=kAP(x+3).

即kAPx-y+3kAP-2=0.

则圆心(2,1)到直线l的距离

去分母两边平方,得

变式2已知实数x,y满足x2+y2-4x-2y-4=0,则3x+4y的最大值为____.

解析将已知条件中的方程配方、整理为圆的标准方程(x-2)2+(y-1)2=9.

故3x+4y的最大值为25.

变式3已知实数x,y满足x2+y2-4x-2y-4=0,则(x+2)2+(y-5)2的最大值为____.

解析将已知条件中的方程配方、整理为圆的标准方程(x-2)2+(y-1)2=9,则(x+2)2+(y-5)2表示圆上一点(x,y)与定点(-2,5)距离的平方.

由平面几何知识可知:在定点与圆心连线所在的直线和圆的两个交点处取得最大值和最小值.

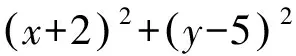
二元条件最值问题种类众多、情形复杂.如果既改变高考题已知条件中的方程,又改变结论中的目标式,可有:

变式4已知实数x,y满足2x2-2xy+y2=1,则x+2y的取值范围是( ).

A.[-5,5] B.(-5,5)

解析由2x2-2xy+y2=1,得

所以由柯西不等式,得

故选C.

变式5已知正实数x,y满足xy(x+2y)=16,则x+y的最小值为____.

解析令x+y=t,则由xy(x+2y)=16,得

(t-y)y(t+y)=16.

所以由三元均值不等式,得

所以f(y)的最小值为f(2)=12.

即t2的最小值为12.

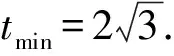
变式6已知实数x,y满足2y2-x2=4,则|x-2y|的最小值为____.

设与直线x-2y=0平行的直线x-2y+t=0与双曲线2y2-x2=4相切,则|x-2y|的最小值即为两平行线x-2y=0与x-2y+t=0的距离.

联立x-2y+t=0与2y2-x2=4,得

2y2-4ty+t2+4=0.

由△=16t2-8(t2+4)=0,得t2=4.

所以|t|=2.

故|x-2y|的最小值为2.

在解题中,若对典型试题就题论题、浅尝辄止,则是死水一潭.而重视问题的一题多解、一题多变,则能激活思维、提振士气.唯有如此,才能逐步培养学生灵活多变的思维品质,提高其数学核心素养,培养其探索精神和创新意识,从而真正把对能力的培养落到实处[3].