生动课堂：促进深度学习的课堂教学

夏胜利

“生动课堂”是通过生生互动、师生互动等方式，引导学生学会学习的课堂。生动课堂中，教师通过热身、探究、拓展、评价等活动，促进学生情动、手动、脑动、口动，实现深度学习。

一、热身：营造学习氛围，让学生情动

情动指学生产生了探究新知的意愿。在热身环节，教师可以通过创设情境激活学生的原有认知，引发学生的认知冲突，以营造积极的学习氛围，激发学生的探究兴趣。

执教人教版数学九年级上册《日常生活中的概率问题——用列举法求概率》时，笔者设计了如下情境问题。“①周一早上，闹钟响了，小明迷迷糊糊地从两双颜色相近的袜子中拿了两只穿上。请你求出小明穿对袜子的概率。”“②小明到达学校后，发现自己忘记带作业本了，于是给爸爸打电话。爸爸的手机号码为18976234132，可是小明又记不清了。若小明忘记了号码的倒数第2个数字，则小明能一次拨通爸爸电话的概率是________；小明第1次未能拨通，但是第2次拨通爸爸电话的概率是________；试猜想，小明前2次未拨通，但是第3次拨通爸爸电话的概率是________；小明前8次未拨通，但是第9次拨通爸爸电话的概率是________。”笔者围绕生活创设情境，引发了学生主动探究生活中概率问题的兴趣，为用列举法求概率做了铺垫。

二、探究：提供学习支架，让学生手动

手动指学生通过画图、计算、操作、实验等主动寻找问题解决方案的过程。探究环节，教师可以通过提供问题支架引导学生“手动”，解决基础问题要素变换后的一系列实际问题，并简要梳理解决该类问题的通理通法。

执教人教版数学九年级上册《实际问题与二次函数：图形面积问题》（第1课时）时，笔者先呈现图1（在直角△AMN中，AN=40m，AM=30m。在它的内部作一个矩形ABCD，其中AB和AD分别在两直角边上），并提供前两个问题支架：①如果设矩形的一边AB=[x]m，那么AD边的长度如何表示？②如果设矩形的面积为ym2，当[x]取何值时，[y]的值最大？最大值是多少？

学生充分思考后发现，先根据相似三角形的性质定理“相似三角形的对应边成比例”，列出算式[30-AD/30=x/40]，算出AD=30-[（3/4）x]，再根据面积计算公式，得出[y]与[x]的关系式[y=x（30-（3/4）x）]，进一步计算得出：当[x]取20时，y的值最大，最大值是300。随后，笔者出示第3个问题支架：“如何找出直角三角形内部面积最大的矩形？”学生探究后发现：①由△MDC∽△MAN可得AD和AB的关系，进而求得矩形面积y；②从图形中可知“长方形的面积=大三角形的面积-两个小三角形的面积”，进而表示出函数y；③由函数y的图象出发，用配方法或公式法求解矩形的最大面积。最后，笔者引导学生梳理、总结解决此类问题的基本思路。学生总结出“设未知数—列二次函数表达式—用配方法化简二次函数—求二次函数最值”4个步骤，并将其记录下来。

三、拓展：联系实际开展变式练习，让学生脑动

脑动指学生迁移运用所学的思想方法的过程。拓展环节关注学习内容的应用、关联与拓展，教师要依据学生课堂探究的实际，生成拓展资源，引导学生在变式练习中迁移运用习得的思想方法。

执教人教版数学九年级上册《实际问题与二次函数：图形面积问题》（第2课时）时，笔者设计了如下发散性问题，引导学生开动脑筋，联系生活实际深入思考。

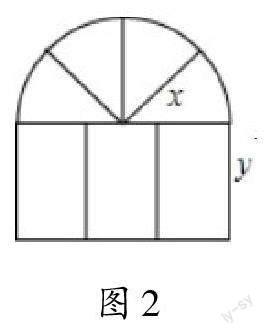
某建筑物的窗户如图2所示，它的上半部分是半圆，下半部分是矩形，制造窗框的材料总长（图中所有的黑线的长度和）为15m，则y与x的函数解析式为________，窗户的面积S与x的函数解析式为________，当x≈      时，S最大且S≈________（结果精确到0.01m2），此时窗户通过的光线最多。

学生对比第1课时内容，发现第2课时中的问题情境已由三角形拓展为组合图形，函数解析式已从求矩形面积发展到求半圆面积，所以解题的关键是由设直角边长转变为设圆的半径。学生在拓展研究“何时窗户通过的光线最多”问题时经历了如下思维过程：①理解问题情境；②分析问题中的变量和常量及其关系；③用函数模型表示变量间的数量关系；④确定函数模型的最值；⑤检验模型结果的合理性并拓展应用模型；⑥总结求解该类型问题的一般方法。学生在笔者的引导下联系实际进行变式练习，运用课堂所学的数学思想方法解决了拓展问题，锻炼了数学思维。

四、评价：激励学生多维观察，让学生口动

口动指学生依据评价量表，自主分析自身的课堂参与情况，并简要分析他人的课堂参与情况。生动课堂教学评价重视学生核心素养尤其是创新精神和实践能力的发展，教师可以引导学生根据过去的基础和现实表现，围绕“自主学习”“独立思考”“对话分享”等学习过程展开自评和互评，进而正确地认识自身优势与不足，科学地确定发展目标，释放自身发展潜能。

人教版数学八年级上册《镶边与剪纸》的教学重点是设计并制作一个镶边或剪纸图案。教学前，笔者呈现了细化的学生课堂参与状况评价量表——“自主学习”考查作品完成度、材料选择、技能掌握、记录与反思等；“独立思考”考查创意与原创性、问题独立解决等；“对话分享”考查作品展示、团队合作与交流、反馈与建议等。其中，“自主学习”的具体观察点是：“学生能否按时完成作品？作品的完成度如何？”“学生能否根据设计要求选择合适的材料，是否尝试使用不同的材料？”“学生能否熟练运用所学的镶边与剪纸技巧？”“学生是否在制作过程中记录了学习和制作的过程？是否对遇到的问题和解决方案进行了反思？”

学生A设计的是一个中心是五边形、内外各有五个小五边形呈轮辐式排列的双色图案，整体呈现发光的星星的視觉效果。学生B设计的是半圆和直线交错的图案，整体呈现太阳射线的视觉效果。自评与互评环节，学生A先做出“我的作品虽然设计简单，但利用了对称图形的性质，纸边裁切整齐，双色搭配得当”的自评，再指出“学生B的作品在几何变换和对称性上做得更好，但裁切得不够整齐”。学生B先做出“我的作品运用了圆和线的几何知识，以及相交和平行的概念，图案与众不同，但裁切不够精准，需要进一步改进”的自评，再指出“学生A的作品展现了良好的对称感，裁切整齐，镶边精准，如果能尝试组合更多的形状会更好”。这样的课堂评价让学生理性分析自己及他人的作品完成情况，推动了作品的改进与完善，提升了学习效果。

（作者单位：武汉市光谷第二初级中学）