计及混合交通均衡的电力-交通耦合网络扩展规划

朱理文, 何 俊, 黄文涛

(湖北工业大学太阳能高效利用及储能运行控制湖北省重点实验室, 湖北 武汉 430068)

电动汽车(electric vehicle,EV)因其低功耗和无污染的特点,符合低碳出行理念,近年来逐渐受到人们追捧,保有量正在快速增加[1]。而大规模EV出行所产生的交通负荷和充电负荷进一步加强了交通网和电网之间的耦合。一方面,大规模的充电需求聚集会增加交通道路拥堵甚至瘫痪风险[2];另一方面,如果对这些充电负荷不加以控制,会造成城市电网负荷峰上加峰[3],电压越限[4-5]等。因此,确保交通网和配电网安全运行下能够满足更多EV的出行需求,研究电力-交通耦合网络(coupled electric-traffic networks,CETN)的扩展规划建设具有重要意义。

EV保有量的增加意味着需要投入更多的充电设施来满足它的充电需求,充电设施的规划通常会考虑配电网经济和安全运行约束,来降低电力系统升级带来的投资成本。文献[6]针对电动汽车充电站接入配电网后构建了线路的可用裕度模型,为今后更多充电站接入下的线路扩展建设留有余地。为防止配电网电压越限,文献[7]建立了充换电站对用户捕获程度最大、配电系统网络损耗最小和配电系统电压偏移最小的多目标规划模型。文献[8]则以充电网服务质量和配电网电压稳定性指标建立目标函数对充电站位置进行优化。文献[6-8]考虑了配电网经济和安全运行约束,但却忽略了交通网特性。对此,文献[9]提出了一种计及充放电管理的充电站规划模型,该模型加入了基于用户均衡(user equilibrium,UE)原理的交通分配模型,以捕获交通网中的交通流分布。但却没有考虑EV车主在出行路径上的道路扩展规划。

电动汽车出行同样会对交通网的运行产生影响,一些学者对规划模型的研究考虑了交通网特性。文献[10]提出了一个多周期充电站扩展规划模型,该模型结合了交通网的拓扑结构和电动汽车有限的行程范围。文献[11]使用真实个人出行调查数据来模拟交通流分布,从而更准确地估计电动汽车充电需求,为充电站的规划提供参考。随着EV的数量增加,其相应的出行需求也会增加,仅依靠交通流分配不足以解决道路拥堵问题。文献[12]提出一种通用的离散网络设计问题公式,用以确定最佳新建道路及其最优容量。电动汽车的加入将使交通网和配电网之间的耦合作用越来越显著,为了在CETN安全运行下能够满足更多电动汽车在交通网中的出行,电力-交通系统的协调规划也越发重要。

针对以上问题,本文提出计及混合交通均衡的电力-交通耦合网络扩展规划方法。首先,在构建配电网和交通网耦合网络的基础上提出了电力-交通耦合网络双层规划模型,上层模型是以道路通行时间、道路扩容、新建充电桩、变电站扩容和新建配电网线路的成本之和最小为优化目标建立的规划模型,下层模型是考虑了充电站拥堵效应和道路扩容,基于用户均衡原理建立的混合交通流分配模型。上层和下层模型充分考虑了电力-交通耦合网络安全运行约束,通过混合粒子群和IPOPT求解器进行求解。算例分析表明,文中所提模型能够在EV不同出行需求下给出最优的扩展规划策略。

1 电力-交通耦合网络构建

1.1 交通网建模

1)道路a上的流量与路径流量守恒

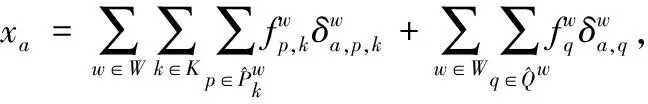
(1)

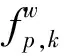
2)每个OD对上出行流量守恒

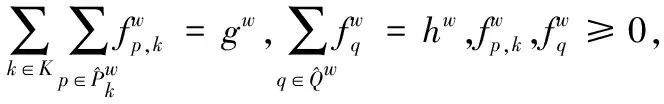
(2)

式中:gw和hw分别为EV和NV在OD对w上的出行需求。

3)道路通行时间

道路通行时间是反应交通网拥堵状况的重要指标,根据美国联邦公路局函数[13],其大小与道路容量和车流量有关。当道路通行容量一定时,通行时间会随着车流量的增大而快速增加,这会给车主的出行带来很多不便。可以通过改变道路通行容量ca来对其进行扩容[14],则考虑道路扩容后的通行时间

(3)

式中:ta表示车辆通过道路a的时间;σa表示道路a的扩建数量,σa≥0;Δc表示扩建一条道路所能增加的通行容量。

4)充电站拥堵效应

充电站为EV提供电能会吸引充电需求。当站内充电桩的数量不能满足充电需求时会产生拥堵效应[15],即EV将面临充电排队时间。排队时间的大小与充电站的服务能力和前往充电的EV车流量有关。假设s为充电站所在节点,仿照BPR函数,则考虑充电站扩容后的充电排队时间

(4)

1.2 电力-交通耦合网络拓扑

交通网中有充电需求的EV通过充电站大规模接入电网后,会对电网安全运行造成影响,这也进一步加强了两个网络之间的耦合关系。在交通网中EV的出行具有很强的随机性,且在配电网中又作为一种间歇性强的用电负荷[16],因此,在EV大规模接入下对电力-交通耦合网络建模具有必要性。则建立耦合网络的拓扑可以抽象表示为

(5)

(6)

式中:Δ为节点道路关联矩阵;当交通网节点i(i=1,2,…,Nm,Nm代表交通网节点总数)在道路a(a=1,2,…,Am,Am代表道路总数)的首端时yia=1;当节点i在道路a尾端时yia=-1,否则为0;S为配电网与交通网的耦合节点矩阵,也是充电站建设节点矩阵;n为耦合节点上建设的充电站总数。

2 考虑混合交通均衡的双层扩展规划模型

在本文所提双层规划模型中,上层规划模型需要合理考虑设备扩展建设的数量,使投资建设成本最小;下层的EV和NV用户则根据上层的规划及交通道路拥堵状况决定自己的出行路径,使自身的出行成本最小。下层的优化结果返回至上层,在电力-交通耦合网络安全运行条件下,根据下层结果调整规划方案,直至上下层在约束下都达到最优结果。

2.1 上层电力-交通耦合网络扩展规划模型

2.1.1目标函数上层的规划模型是以电力-交通耦合网络扩展规划成本之和最小为优化目标,其中交通网扩展规划成本包括道路扩容、充电站内新增充电桩和交通网通行时间成本;配电网扩展规划成本包括新建线路以及变电站的扩容成本。具体的数学模型为

minFu=CTN+CPDN

(7)

(8)

(9)

(10)

(11)

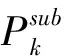
2.1.2约束条件

1)设备扩展建设数量约束

0≤σa≤σa,max

(12)

0≤hs≤hs,max

(13)

0≤nij≤nij,max

(14)

式中:σa,max为道路a扩容数量上限;hs,max为新增充电桩数量上限;nij,max为新建配电网线路数量上限。

2)充电站服务能力约束

为了避免充电桩数量不足给EV车主带来长时间充电排队时间,充电站服务能力应不小于充电车流量,则

xs≤(cs+hs)·Δs

(15)

3)道路通行能力约束

道路上的车流量不能超过其通行能力上限,则

xa≤ca+Δc·σa

(16)

4)配电网安全运行约束

为了提高计算速度,配电网潮流和电压分布采用简化的Distflow形式[17],则简化后的节点电压幅值上下限约束、线路有功功率容量约束、节点电压降关系约束和支路有功和无功潮流约束可以如下所示:

(17)

5)耦合节点功率约束

分析可知，界面剪应力沿锚固长度呈递减规律分布且具有一致性，界面剪应力在锚固外端口具有最大值。通过公式计算、数值模拟和张拉试验得到的结果相差不大。由于张拉试验中锚固外端施加了约束垫板造成应力集中，故得到的端口剪应力数值大于公式计算结果。公式计算得到的锚固尾端界面剪应力稍大，主要因为在方程求解时，以锚杆尾部轴力为零作为边界条件导致轴力骤降所致。

对于电力-交通耦合网络,假设配电网节点上有常规负荷以及电动汽车出行路径上产生的充电负荷,则在耦合节点上的功率需求可以表示为

(18)

6)投资预算约束

折算至每年的道路扩容、新增充电桩、新建配电网线路和变电站扩容成本之和应在投资预算范围内,即

κ(c1+c2+c3+c4)≤ctz

(19)

式中:ctz为年投资预算的最大额度。

2.2 下层混合交通均衡模型

2.2.1目标函数根据 Wardrop 用户均衡理论[18],车主在交通网中的出行路径一般会选择出行时间最小的那一条,而车主的路径选择行为会产生交互影响,导致交通网中各条道路上的车流量发生变化,并最终达到均衡状态。均衡状态下每位车主的出行时间都不能通过改变自身的路径选择而减少,且车主在OD对上各条路径的通行时间相同且最小。因此,本文所提下层模型实际上是交通流量分配问题,EV和NV车主根据上层规划决策,选择出行时间成本最小的路径。则基于UE理论,具体的混合交通均衡为

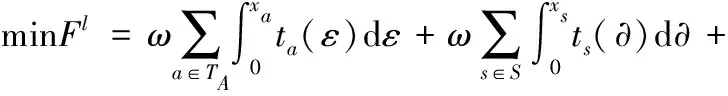
(20)

s.t.式(1)-(2)

(21)

(22)

(23)

(24)

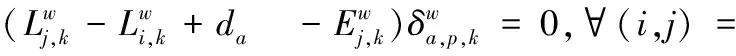
(25)

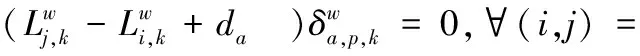
(26)

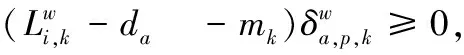
(27)

(28)

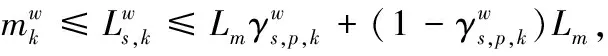
(29)

(30)

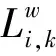
NV的最优出行路径仅需考虑道路通行时间成本,则

(31)

(32)

3 电力-交通耦合网络扩展规划求解流程及算法

本文所提考虑混合交通均衡的电力-交通耦合网络扩展规划模型中,上层和下层模型都是一个多变量和非线性的优化问题,随着网络规模的变大,求解难度也将增加。因此,本文在上层扩展规划模型中借助混合粒子群算法进行求解,算法参数可以参考文献[21-22]。下层混合交通均衡模型可以借助IPOPT等求解器进行求解,具体的扩展规划求解流程见图1。

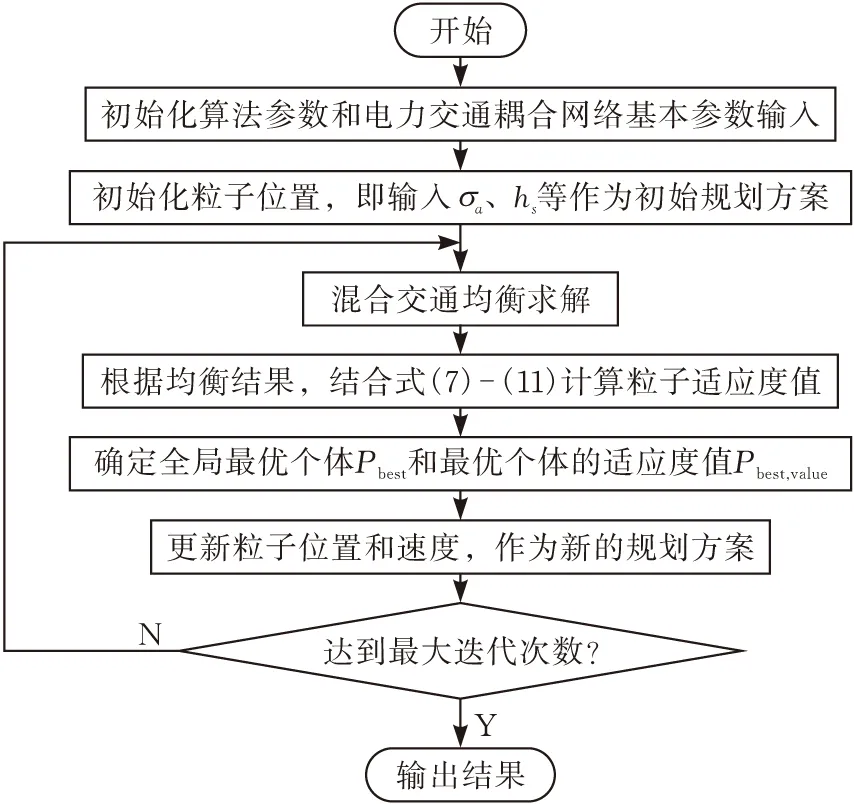
图1 电力-交通耦合网络扩展规划流程

步骤1:初始化算法参数和基本参数输入。基本参数包括交通网道路参数、配电网节点线路参数、投资成本参数、充电站参数、耦合节点信息以及EV和NV出行需求等。

步骤2:初始粒子位置。在约束范围内,生成初始粒子位置并将其作为初始的上层规划方案,传递至下层模型。

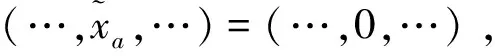
步骤4:计算粒子适应度值。在获得最终交通均衡状态后,将道路流量分配结果和各充电站充电车流量结果返回至上层,根据式(7)-(11)计算适应度值,对于不满足约束条件的粒子设置惩罚值,最终的适应度值为式(7)加上惩罚值。

步骤5:确定全局的最优个体Pbest和最优个体的适应度值Pbest,value。

步骤6:更新粒子的位置和速度并将其作为新的规划方案。

步骤7:终止条件。检测是否达到最大迭代次数,若达到最大迭代次数则输出最优的扩展规划结果;否则,返回步骤3。

步骤8:输出最优规划结果并进行统计。

4 算例分析

4.1 基本参数

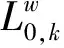
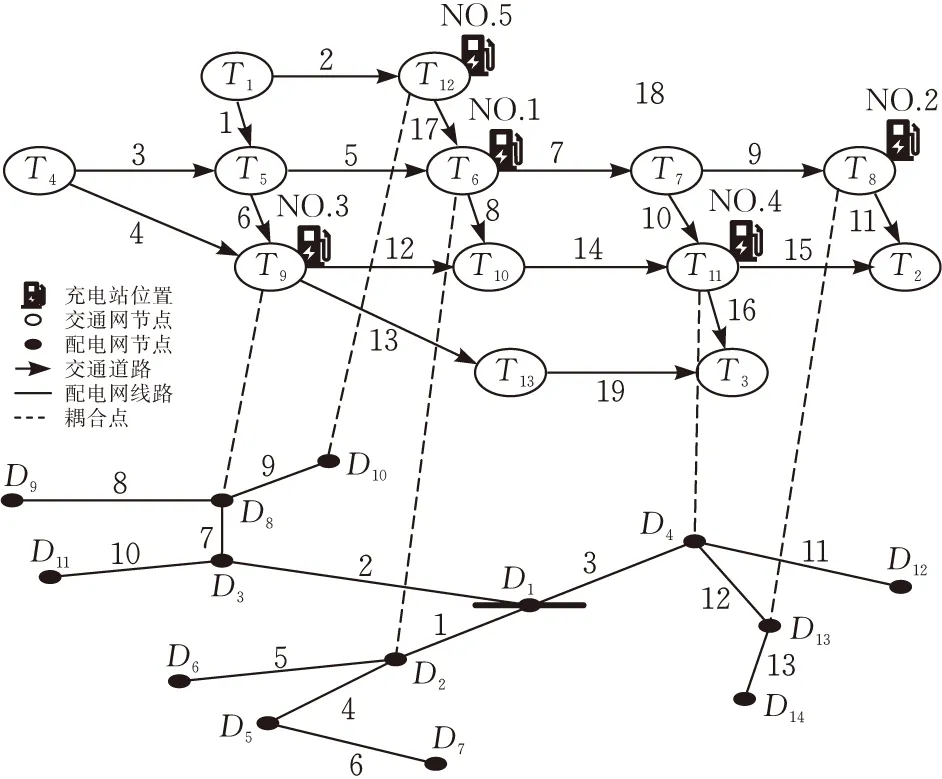
图2 交通网和配电网耦合拓扑结构

4.2 仿真结果和分析

为了验证文中所提的扩展规划模型,考虑了交通均衡下5种不同的交通出行场景,即在OD对间普通汽车出行需求不变的情况下,电动汽车的出行需求分别增长0、25%、50%、75%和100%,来模拟电力-交通耦合网络下电动汽车在不同出行渗透率下的扩展规划策略。扩展规划模型的投资成本结果如图3所示,相应的道路扩容、新增充电桩和新建配电网线路数量如图4所示。

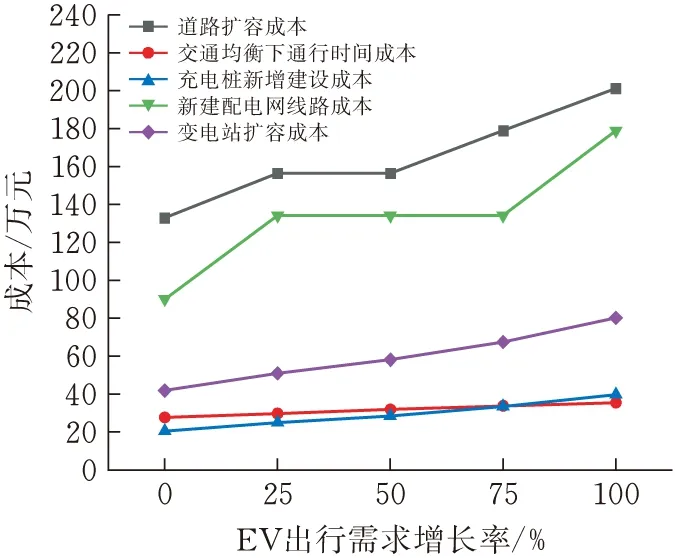
图3 不同场景下扩展规划成本

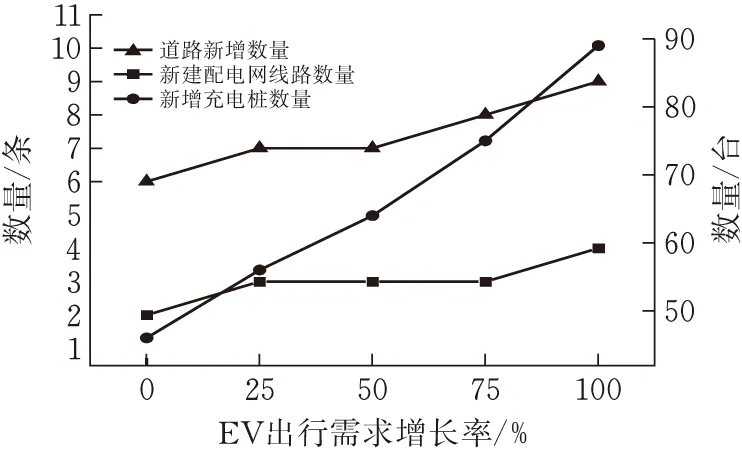
图4 不同场景下扩展规划数量

在图3和图4中,随着EV出行需求的增加,扩展规划模型中各设施的投资成本和规划数量都呈现出增长趋势。其中,道路扩容成本和配电网新建线路成本在整个投资成本中占主要部分,说明扩展规划策略需要加大对这两个方面的投资来满足EV出行需求增长而带来的交通负荷和充电负荷的增长。

4.2.1道路扩容分析交通道路在EV不同出行场景下最优扩容的具体位置和数量见表1。

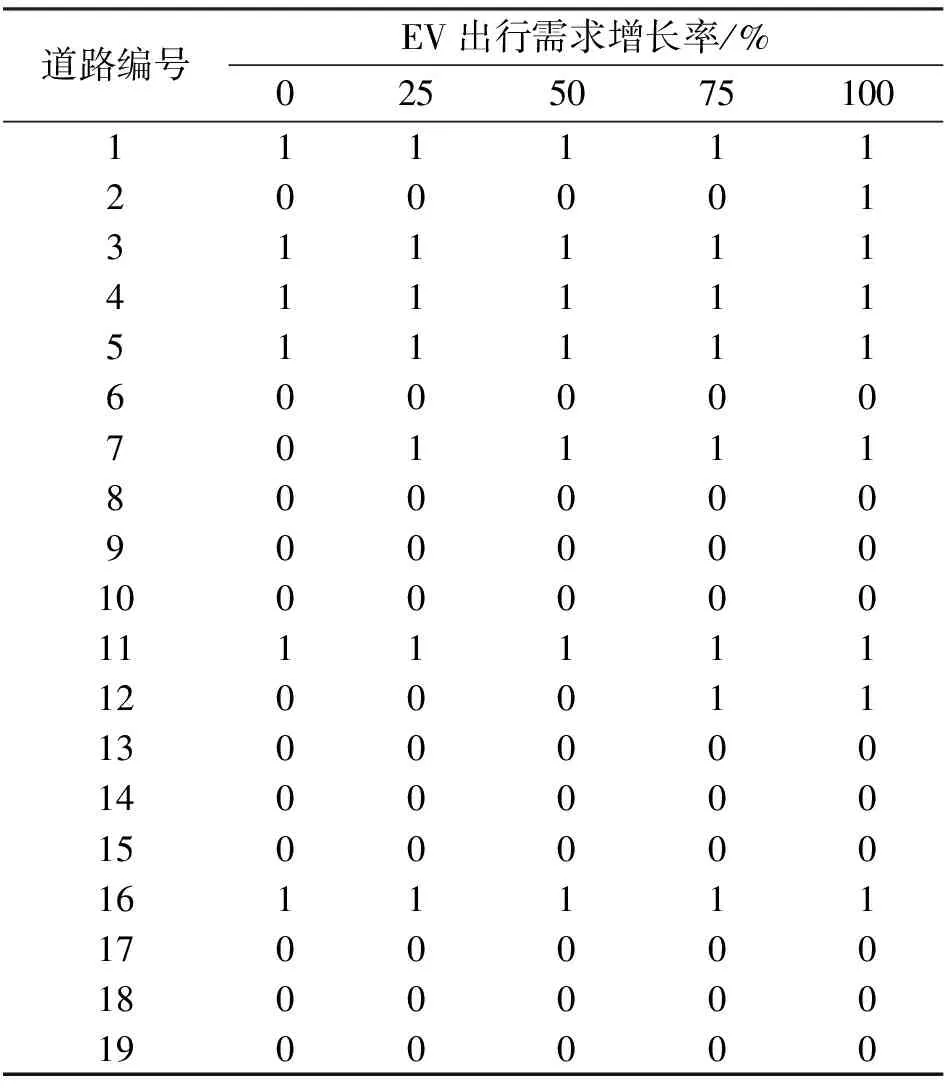
表1 道路扩展规划策略

从表1中可以看出,每条需要扩容的道路在扩建1倍后都可以满足EV出行需求增加的5种场景,而不需要继续扩容。并且,交通网中道路的扩容倍数并不会随着EV出行交通量的增加而增加,如在EV出行需求增加25%和50%的场景,这两个场景下的规划策略相同。因为当道路扩容后,原有的道路容量增加了,但在交通均衡状态下通过道路的车流量并不会大幅增加使其超过扩容后的道路容量。

图5和图6给出了EV出行需求增加0和100%场景下各道路的实际车流量。

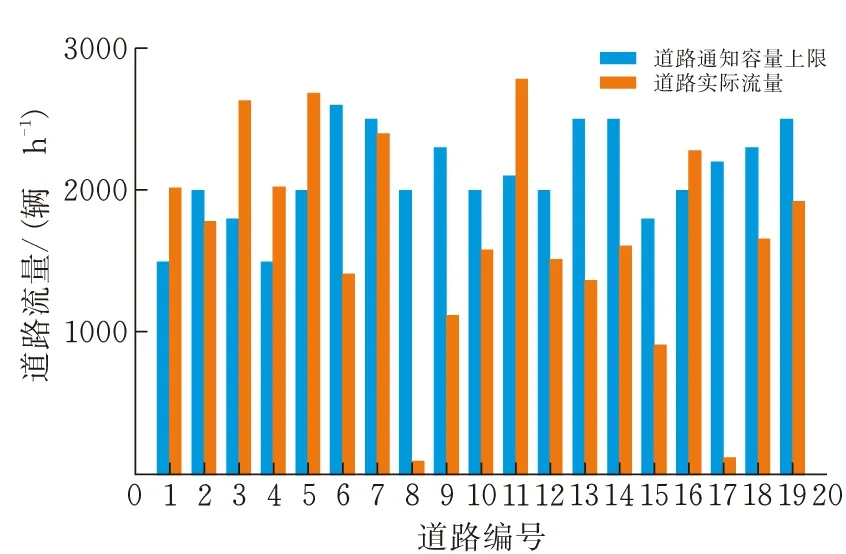
图5 EV出行需求增加0时各道路车流量

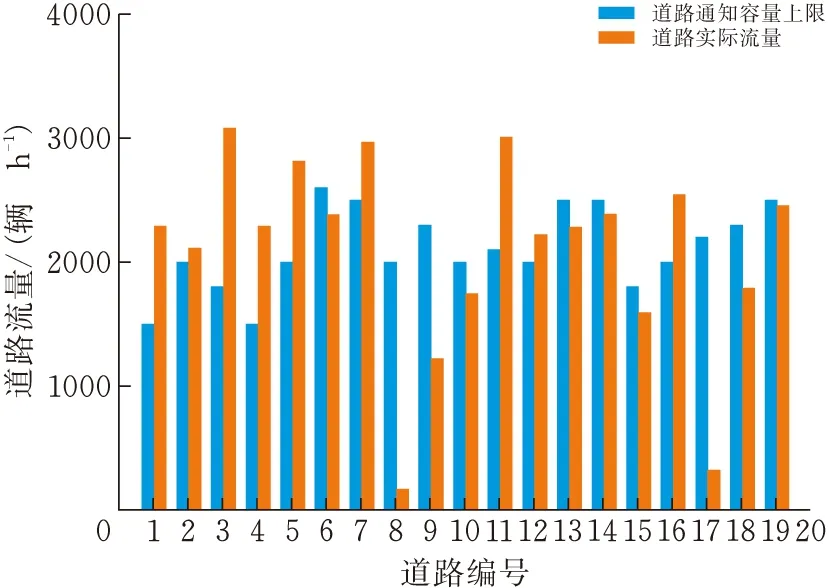
图6 EV出行需求增加100%时各道路车流量

从图5和图6中可以看出,随着EV出行需求的增加,将导致一些路段的车流量增加,使道路的实际车流量超过通行容量上限。在图6中,不进行扩容的道路3和4在交通均衡下的实际车流量分别为3082和2292,分别超过了其容量上限的71.1%和52.8%,其通行时间也会大幅增加。因此,扩展规划策略需要对这些道路进行扩容,在EV出行增加0场景下有6条道路需要扩容,而在EV出行增加100%场景下有9条道路需要扩容。两个场景下道路扩容前后的通行时间如图7和图8所示。

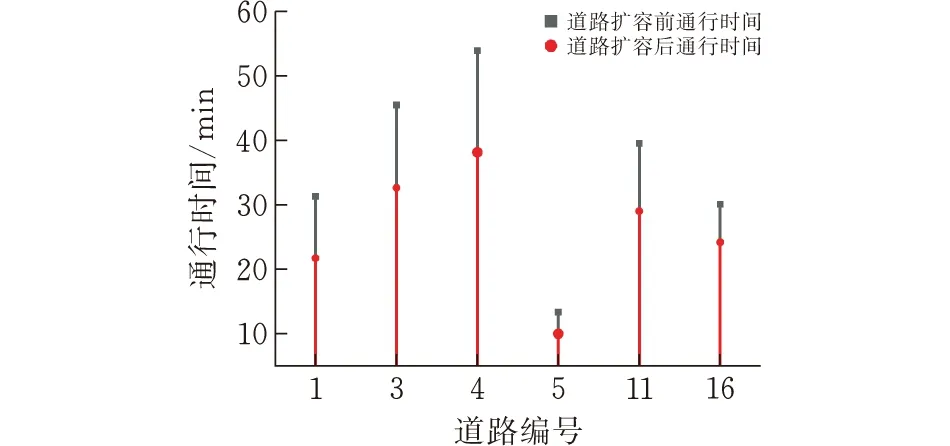
图7 EV出行需求增加0时扩容道路通行时间

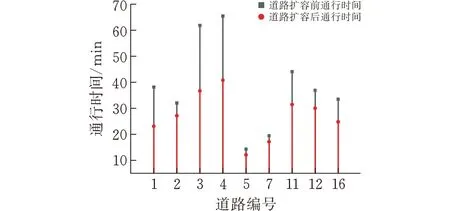
图8 EV出行需求增加100%时扩容道路通行时间

在图7和图8中,交通均衡下道路不进行扩容的通行时间会随着EV出行需求的增加而增加,如道路3在EV出行增加0%时通行时间为53.8 min,在EV出行需求增加100%时通行时间达到了61.8 min。而两个场景下道路的通行时间在经过道路扩容后都降低了,提高了车主出行的便捷性,说明在扩展规划模型中道路扩容的有效性。

4.2.2新增充电桩扩展规划分析5种场景下,各充电站内新增充电桩的数量如表2所示。

表2 充电桩扩展规划策略

从表2中可以看出,随着EV出行需求的增加,各充电站内新增充电桩的数量都呈现增加趋势,而充电站NO.1新增充电桩数量最多,因为它所在的交通网节点有多条路径经过,会带来更多充电需求。图9给出了它在不同场景下充电桩新增前后的充电排队时间。充电站NO.4原有的充电桩数量能够满足增长的充电需求,因此它新增的数量不多。

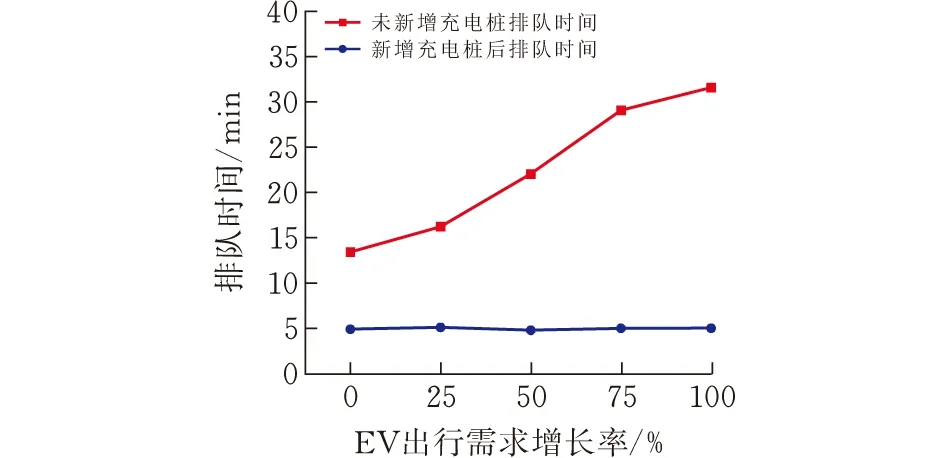
图9 充电站NO.1在不同场景下的充电排队时间

图9中,在充电站NO.1新增充电桩前,各场景下都有较长的充电排队时间。在进行扩建后,车主的充电排队时间都有较大减少,说明扩建充电桩能够有效改善车主充电体验,提高充电的便捷性。

4.2.3耦合网络下配电网扩展规划分析不同场景下配电网新建线路的具体位置和数量见表3。

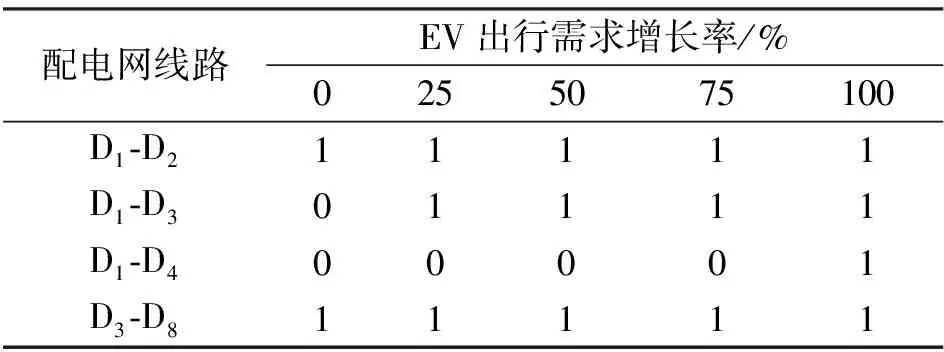
表3 配电网线路扩展规划策略

在表3中可以看出,EV出行需求增加25%场景下的规划策略能够满足出行需求增加50%和75%两个场景。耦合网络下,充电需求给电力节点带来新的负荷,随着EV出行需求增加100%,产生大量的充电负荷,此时线路传输的有功功率将超过其容量限制。因此,需要对线路D1-D2、D1-D3、D1-D4和D3-D8进行扩建,以确保电力能够持续输送到充电站。

4.2.4敏感性分析考虑车主在最短路径方式下出行和在交通均衡下出行,将两种模式进行对比。则在电动汽车的出行需求增加100%场景下的通行时间成本如表4所示。

表4 不同出行方式通行时间成本对比

通过对比表4中的通行时间成本,车主在交通均衡下通行时间成本比最短路径下小,因为当车主都选择最短路径出行时会导致交通拥堵,其通行时间反而会大幅增加。而交通均衡下路径上的通行时间都达到了均衡状态,其通行时间成本也会更小。

5 总结

本文提出了计及混合交通均衡的电力-交通耦合网络扩展规划方法,建立了以投资建设成本最小的上层规划模型和混合电动汽车和普通汽车的下层交通流分配模型,通过混合粒子群算法和IPOPT求解器进行求解,确定了电动汽车在不同出行场景下的最优扩展方案,研究结论如下:

1)OD对出行需求的增加会导致一些道路通行容量超过其限制,进而导致通行时间大幅增加。考虑道路扩容方案能够有效改善通行时间,为车主出行带来便利,这也验证了本文扩展规划模型解决道路拥塞问题的有效性。

2)道路上的充电需求会给耦合网络下的配电网节点引入新的负荷,规模化充电负荷接入会导致一些配电网线路的有功功率超过其容量限制,需要对线路进行扩展建设来保证电力的传输。

3)相较于最短路径出行,采用交通均衡模型更能反映实际道路通行状况和车辆间的交互影响,改善交通网系统的运行和车主出行时间。