基于Hoek-Brown准则等效强度参数的工程应用

胡其志, 刘 倩

(湖北工业大学土木建筑与环境学院, 湖北 武汉 430068)

21世纪以来,我国西部地区公路、铁路建设迅猛发展,对公路、铁路隧道的要求也逐渐趋向“大”“宽”“深”等方面。但西南部地区地质情况复杂,岩体多呈层状,对隧道的开挖和支护有着极大影响。由于层状岩体具有各向异性的力学性质,使得其与普通围岩相比,研究更为复杂,也更有必要。

大量学者针对岩体特性及强度参数进行了研究,这其中,自1980年发展至今的H-B准则[1-2]在描述岩体破坏方面充分考虑了隧道爆破、岩体性质等,取得了较好的效果;张玉军、张思渊[3]以修正的H-B准则为理论依据,利用横观各向同性二维有限元程序对不同倾角层状围岩条件下的矩形洞室进行计算分析,认为层状岩体各向异性对围岩稳定性具有较大影响;张标[4]基于H-B准则利用FLAC3D模拟了不同工况下理想弹塑性围岩的开挖,由围岩纵向变形曲线拟合得到修正的非线性位移公式;李伟瀚、张彬[5]等以贵阳市黔春大道七冲村二号隧道为工程背景,分别应用M-C准则和H-B准则,采用FLAC3D进行模拟,发现两种准则所得位移、应力等变化趋势相同,但在低地应力情况下M-C准则适用性更好,与现场监测对比发现H-B准则更具有相关性。胡炜、谭信荣[6]等郑万线某隧道为背景,针对地质顺层偏压问题,采用理论分析、数值模拟对其不同结构面参数下的破坏机理进行了研究,发现围岩塑性区范围随结构面内摩擦角增大而减小,当结构面内摩擦角大于等于岩体摩擦角后,结构面内摩擦角对围岩稳定性影响较小。

随着计算机技术的发展,数值模拟软件受到愈来愈多研究者青睐,其中以FLAC3D最为盛行。FLAC3D亦称有限差分软件,囊括众多岩土工程计算模型,以其运行速度快、精确度高而著称。冷先伦,盛谦[7]等将FLAC3D中遍布节理模型和M-C模型进行对比,研究了佛子岭抽水蓄能水电站地下厂房位移、应力和塑性区状态,发现遍布节理模型更适用于节理发育地形;贾剑青,李晶[8]等对共和隧道采用FLAC3D应变软化模型进行数值模拟,得到拱顶位移最大,拱底有膨出,特征面上围岩及支护应力随开挖而增大的结论;王志杰等[9-10]以蒙华铁路阳城隧道为研究对象,采用FLAC3D软件对围岩稳定进行数值模拟,发现不同层厚比土砂互层隧道拱脚位移大于拱肩,且张拉破坏主要发生在沿层理面法线方向;吴旭平[11]利用FLAC3D有限元模拟软件对含软弱夹层浅埋隧道围岩变形特性进行研究,提出围岩变形分级控制指标;李晓红,夏彬伟等[12]将现场监测和有限差分软件模拟相结合,研究了重庆至长沙省际高速公路共和隧道段围岩稳定性,分析其初衬出现变形破坏的原因。但此过程中,由于岩体参数取为完整岩体,导致围岩模拟值与实测值结果误差较大。此外,在采用遍布节理模型对层状岩体进行传统模拟过程中,岩体强度参数始终取为定值,未考虑中主应力、洛德角和岩层倾角对强度参数的影响。因此,可以通过对不同倾角岩体参数进行折减并修正,得到7组等效强度参数,输入遍布节理模型对围岩进行模拟,缩小模拟值与实测值间的误差,提高模拟结果的可靠度,为实际工程提供指导。

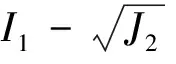
1 修正H-B准则的瞬时等效M-C参数计算

1.1 岩体强度准则

M-C准则是应用最为广泛的强度破坏准则,将其用I1、J2、θσ进行表达可得:

(1)

(2)

但大量研究表明,相较于线性准则,曲线准则能更好的表述高地应力条件下岩体的各向异性。针对M-C准则在描述岩体破坏特性各向异性方面的缺陷,以及在拉应力、低应力和高应力条件下的不足,E.Hoek和E.Brown(1980年)基于Griffith理论,对大量岩体进行单轴、三轴压缩试验并结合工程实际情况,提出了H-B准则:

(3)

式中:σ1、σ3、σci分别为最大、最小主应力和岩体单轴抗压强度,mi、s为岩体经验常数,与岩体完整性、类型、风化程度等因素有关,mi取值参考文献[2]。

H. Saroglou 和G. Tsiambaos在原准则基础上提出适用于层状岩体的修正H-B准则:

(4)

式中:σ1、σ3分别为最大最小主应力;σcβ、kβ为单轴抗压强度和mi修正系数,均由加载方向和节理面的夹角β决定。

将σ1、σ2和σ3用应力不变量I1、J2、θσ代替,有以下转换公式:

(5)

(6)

故修正H-B准则的应力不变量形式为:

(7)

式中:I1、J2分别为应力张量的第一不变量(也称静水压力或平均应力)及应力偏张量的第二不变量,θσ为Lord角,衡量岩体应力状态,取值范围[-30°,30°]。因此,式(7)亦可称为适用于层状岩体的考虑静水压力效应、Lord角效应的三维H-B准则。

1.2 等效M-C强度参数计算方法

由于H-B准则的非线性性,使其在实际应用中较为复杂,而M-C准则为线性准则,且大部分解析式和数值模拟软件均使用M-C准则,因此大量学者提出将H-B准则强度参数等效为M-C强度参数的方法,并应用于工程中。

Hoek提出基于H-B准则将岩体强度参数和M-C准则内聚力和内摩擦角进行瞬时等效,得到:

(8)

其中,

(9)

式中:σn为正应力,h为节理面间距大小。

根据式(8)(9),只要确定了σn的值即可求得相应等效内聚力和内摩擦角。这种等效方法本质上是在指定点处将H-B准则与M-C准则表达式在该点的切线进行等效(图1),解方程得出相应c、φ值,具有简单、方便等特点。

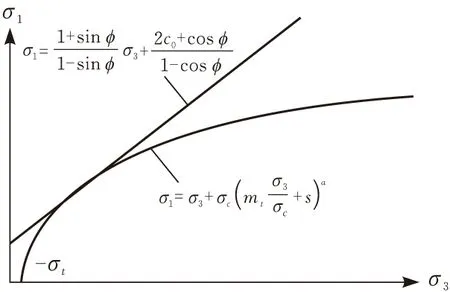
图1 σ1-σ3 平面瞬时等效法

1.3 修正H-B准则等效强度参数计算

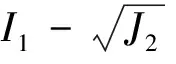
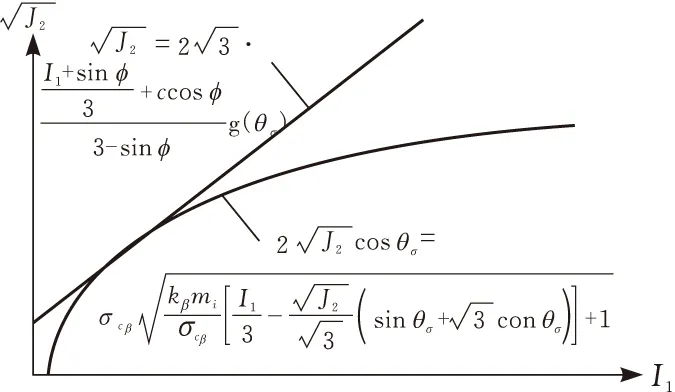
图平面瞬时等效

根据切线等效原理,对给定破坏面上一点(I1,J2,θσ),均有H-B准则在该处切线与相应M-C准则直线重合(如图2),由此可知存在下列等式:

(10)

对式(1)等式两边对I1求偏导可得:

(11)

对式(7)等式两边对I1求偏导可得:

(12)

联立式(11)和(12)即可解出瞬时等效内摩擦角为:

(13)

式中:Cβ为与岩体特性相关的系数

Cβ=σcβkβmi

(14)

根据式(7)可得相应内聚力c的表达式为:

(15)

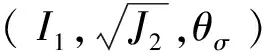
(16)

由于节理若面存在,层状岩体内聚力相较完整岩体更小,故此处引入相应强度折减系数α=0.1,对强度进行折减,故有:

(17)

由以上等效内摩擦角公式可知,对于已知层状岩体,只要确定其极限应力状态(σ1,σ2,σ3)即可算得对应等效M-C准则内摩擦角,将其代入式(17)中,可进一步得到等效内聚力。上述方法将H-B准则在子午面上与M-C准则进行等效,使得针对层状岩体的H-B准则不再局限于二维平面,而是能够从三维空间角度对岩体强度特性进行计算,充分考虑了岩体的中主应力效应、静水压力效应及Lord角效应。

2 工程案例研究

为验证上述等效强度公式对层状岩体的适用性,现以共和隧道为背景进行工程案例研究。西部开发重庆至长沙省际公路共和隧道为双洞分修特长隧道,左右洞长度分别为4779 m、4745 m,两洞轴线相距20～23 m。隧道最大埋深1000 m,属深埋隧道。围岩产状为:300°～325°∠20°～40°(图3),隧道轴线走向231°,与岩层走向交角0°～20°。隧道区位于四川盆地东南端大娄山北西侧,属乌江侵蚀河谷发育的中低山峡谷地区。隧道受地质构造、岩层属性、埋深等影响。其左侧山脉蜿蜒,走向与隧道轴线走向基本一致,呈北北东-南南西向延伸,右侧紧邻乌江。

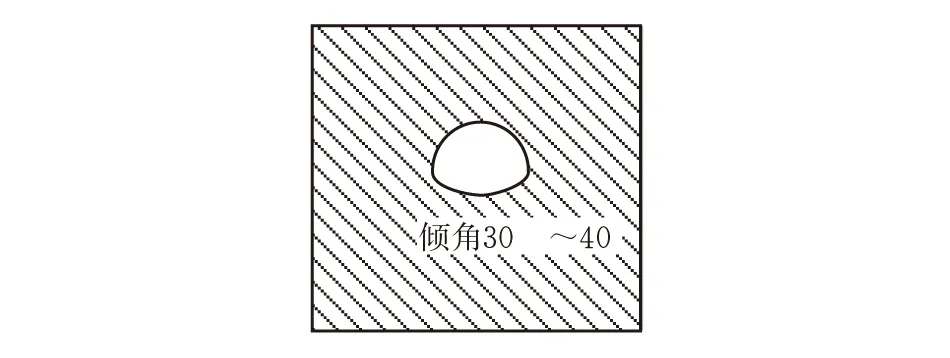
图3 隧道岩层构造示意图

最大埋深处围岩为Ⅲ级,隧道区内为单斜构造,无其他复杂地质。隧道穿越地层为志留系上统罗惹坪组砂质页岩、页岩,局部夹粉砂岩。隧道区地应力资料显示,其最大水平应力29.86 MPa,垂直应力27.0 MPa,最小水平应力20.21 MPa。

图4 隧道初支破坏情况

K40+430-K42+230为共和隧道埋深最大区段,围岩等级为Ⅲ级,属硬岩,层间结合较好。页岩裂隙面一般平直光滑,多呈闭合状,无充填或钙质薄膜充填,节理面间距为1～2 m。自K40+830断面开始,隧道右拱肩出现钢拱架扭曲变形,左拱脚初期支护出现喷射砼开裂、掉块等现象(图4),给后续施工和支护带来极大安全隐患。虽由于地势因素,靠山侧地应力大于靠河侧,对围岩破坏有一定影响,但从现场破坏分布来看,隧道变形破坏与围岩性质联系更为紧密。

2.1 建立数值模型

共和隧道K41+567段最大埋深为700 m,初始应力状态为σx=-16.33 MPa,σy=-12.28 MPa,σz=-15.69 MPa,τxy=-0.133 MPa,τxz=-1.095 MPa,τyz=1.945 MPa。依据共和隧道现场监测数据,隧道处于偏压受力状态,由于隧道模拟试验复杂且难以实现,因此数值模拟分析是较为合理的研究方法。

在对层状岩体进行数值模拟方面,衍生出多种计算模型,这其中使用最为广泛的是横观各向同性模型和遍布节理模型,且遍布节理模型更能体现层状岩体强度各向异性特征。但传统遍布节理模型在应用时,导入的岩体强度参数为完整岩体参数,高于实际节理间岩体强度参数,且传统方法中该参数始终为定值,未考虑节理倾角效应,不能充分体现层状岩体各向异性。

因此,选取共和隧道K41+567Ⅲ级围岩区段为研究对象,采用遍布节理模型(biquitous-joint model),提出按倾角不同对强度参数进行修正,再依次导入FLAC3D对层状岩体进行研究的方法(简称参数修正法),对此区段岩层倾角分别为0°、15°、30°、45°、60°、75°、90°的岩层进行数值模拟,并在相同倾角变化条件下,使用传统遍布节理模型模拟方法对层状围岩进行二次模拟,依据文献[17]所得试验结果,取岩体参数c=1.9 MPa,φ=33.7°,节理参数c=0.1 MPa,φ=30°,作为对照。

FLAC3D模型网格划分如图5,相应岩体计算参数根据文献[2]中的GSI法取用。由于研究重点为围岩稳定随倾角变化特征,因此模拟中采用全断面法进行开挖,且暂不进行支护。

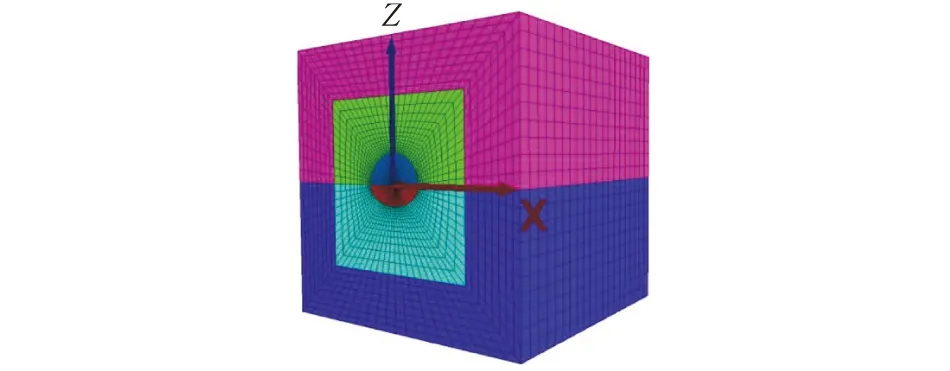
图5 模型网格划分

2.2 强度参数计算

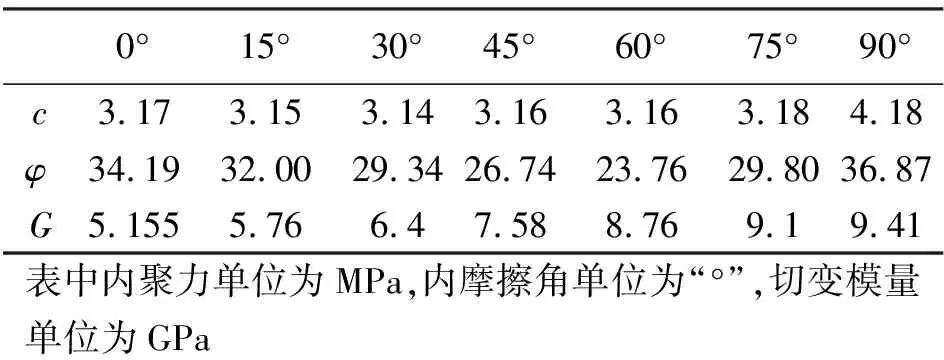
表1 不同倾角岩体等效强度参数

2.3 模拟对比

1)关键点位移量 记录模拟结束时围岩倾角30°隧道断面拱顶、拱底和拱腰等关键位置位移并绘制隧道径向位移分布(图6)。

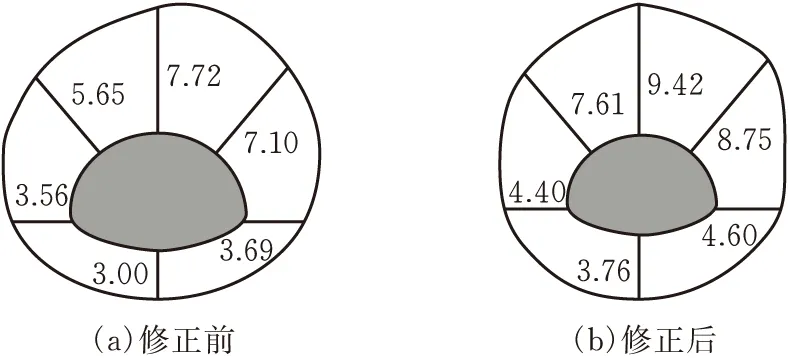
图6 围岩位移分布特征

由图6可知,由于偏压作用影响,隧道右半部变形较左半部更大,径向位移分布图重心偏右。对比岩体参数修正前后水平位移、竖向位移以及径向位移可以看出,根据岩层倾角对岩体参数进行适当修正所得位移与现场监测更为接近。以拱顶竖向位移为例,修正前拱顶竖向位移为7.72 mm,修正后为9.42 mm,现场监测位移为59.22 mm,说明修正后的围岩位移与实际变形更接近,但仍远小于模拟计算值。

图7为不同倾角条件下,隧道各关键点位移数据特征统计。由图7a可以看出,岩体系数修正后拱顶位移量相比修正前有所增大,且位移量变化趋势与修正前基本一致,均为先增大后减小到最后基本持平,但较修正前位移量波动更大。随着岩层倾角的增大,修正前后的拱顶位移差逐渐减小,当倾角超过60°后,位移差为负。说明在当倾角超过60°后,对岩体系数进行修正的方法不再适用。图7b为拱底位移变化特征,观察该图不难发现,拱底位移量修正前后变化规律一致,且修正后的适用范围依旧为0°～60°。

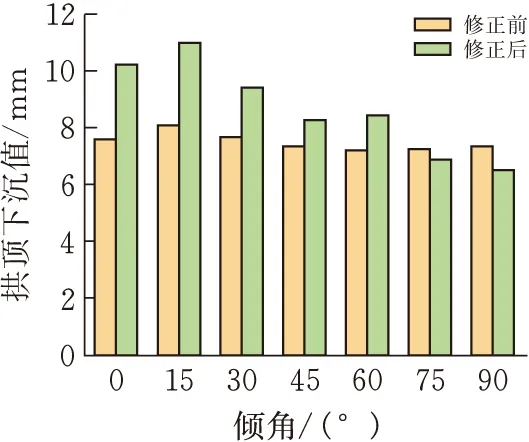
(a)拱顶下沉随倾角变化

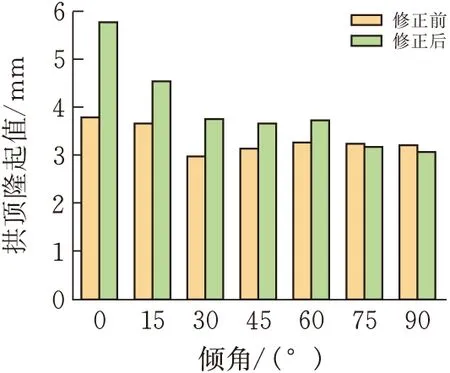
(b)拱顶隆起随倾角变化

(c)拱肩径向位移随倾角变化

(d)拱脚径向位移随倾角变化

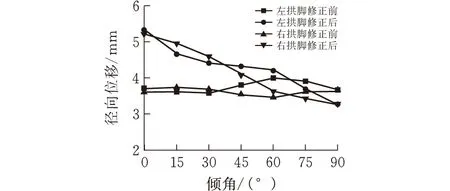
图7c为隧道拱肩位移数据统计图。可以看出,岩体参数修正后,左右拱肩位移量较修正前更大,但当倾角大于75°后,修正后位移量小于修正前,说明此时该方法对拱肩处位移量无扩大作用。且不论修正前或是修正后,右拱肩位移量始终大于左拱肩,与实际工程中右拱肩处钢拱架发生弯曲现象相符。观察图7d可知,修正后拱脚处位移量基本大于修正前,当倾角大于60°后,参数修正法对拱脚处位移量无扩大作用。且不论修正前或是修正后,左右拱脚位移量在倾角0°及90°时基本相等,40°～90°时差异较大,此时左拱脚位移大于右拱脚。

2)关键点应力值 计算结束时修正前后最大主应力分布如图8所示(以30°为例),可以看到,最大压应力呈括弧状围绕于断面外侧,拱顶、拱底部位出现应力集中现象。说明修正前后应力分布形状基本一致,但由数据可知修正后最大压应力大于修正前。

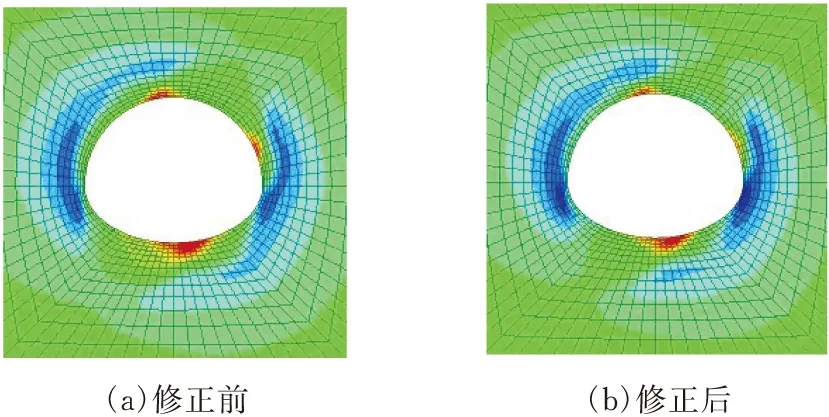
图8 围岩应力分布

为充分体现围岩应力状态,现以(σ1-σ3)为竖轴,倾角为横轴,作围岩最大、最小压应力之差随倾角变化情况以柱状图和折线图(图9)。图9a,b为拱顶、拱底位置(σ1-σ3)统计图,观察图像可知,修正前拱顶、拱底(σ1-σ3)值均小于修正后,且变化趋势基本一致,均为先减小后增大。分析其应力数据发现,拱顶、拱底的(σ1-σ3)值变化范围基本相同,都是0～20 MPa。由图9c知,修正后左右拱肩(σ1-σ3)值均大于修正前,左右拱脚(σ1-σ3)值也大于修正前,说明修正后拱肩拱脚处发生后续变形可能性较修正前更大,采用修正后模拟结果对工程进行指导可进一步提高工程施工的安全性。

应力是影响围岩后续变形的重要因素,因此,综合分析修正后模拟结果可知,参数修正法能够在一定程度上推进施工安全性的加强。

(a)拱顶(σ1-σ3)随倾角变化

(b)拱底(σ1-σ3)随倾角变化

(c)拱肩(σ1-σ3)随倾角变化

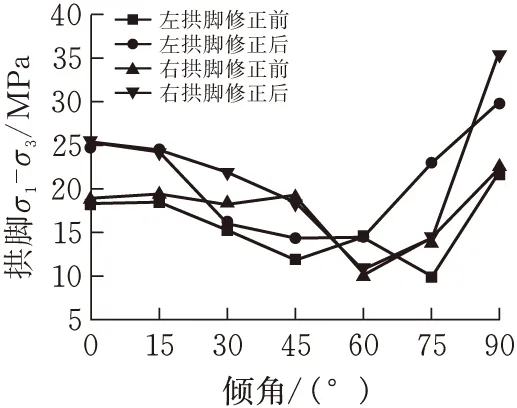
(d)拱脚(σ1-σ3)随倾角变化

3)围岩塑性区 以倾角30°为例,将修正前后塑性区延伸深度分布情况绘制成图(图10)。观察图形可知,当岩层倾角为30°时,围岩塑性区在左侧拱底达到最大,右拱肩次之,与隧道现场破坏情况一致,且参数修正前后塑性区深度相差不大。

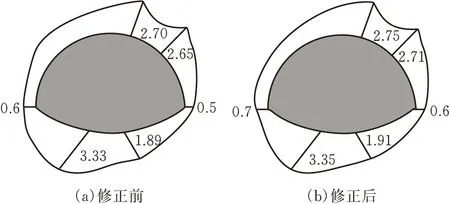
图10 围岩塑性区延伸深度

不同倾角下围岩塑性区分布如表2所示。易知,塑性区形状随倾角的偏转而偏转,且始终沿倾角法线方向发展。对于修正前倾角为0°和90°的塑性区,由于偏压作用,图形呈非对称分布,0°时左拱肩和拱底塑性区深度达到最大,90°时拱腰塑性区深度最大。对岩体参数进行修正后,由于岩体在倾角为0°时的强度参数与修正前有较大差异,塑性区形状较修正前出现明显差异,但0°时其塑性区依旧在左拱肩和拱底达到最大,而90°时拱腰塑性区深度最大,即塑性区特征与原来一致。

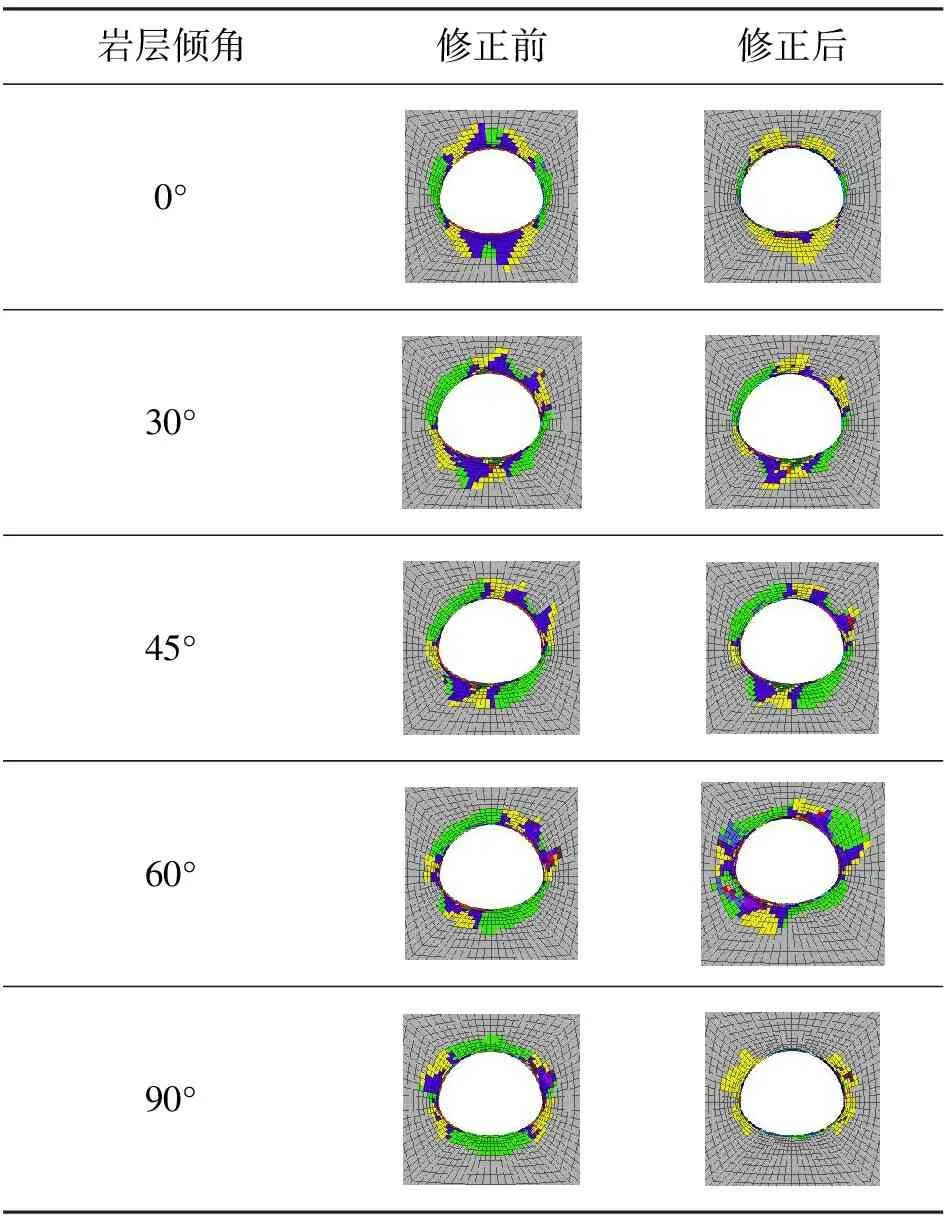
表2 不同倾角下围岩塑性区

此外,当岩层倾角为30°时,岩体内摩擦角为29.34°,略微小于节理内摩擦角(30°),此时围岩塑性区形状饱满,面积适中。此外,横向对比修正前后内摩擦角发现,修正前岩体内摩擦角取33.7°,修正后为34.19°,进一步扩大了岩体与节理内摩擦角差异,因而围岩受到节理影响更大,导致修正后塑性区面积较修正前更小。同理可知,岩层倾角60°时,修正后岩体内摩擦角为23.7°,小于节理面内摩擦角,此时塑性区面积在所有倾角中最大。此外,横向比较修正前后内摩擦角可知,修正后岩体内摩擦角较修正前更小,且小于节理内摩擦角,最终导致修正后塑性区面积大于修正前。因此,由修正后不同倾角条件下岩体内摩擦角和节理内摩擦角大小关系可知,当岩体内摩擦角小于节理内摩擦角时,围岩塑性区面积较大;反之,当岩体内摩擦角大于节理内摩擦角时,围岩塑性区面积较小。

3 结论

1)采用修正岩体参数法所得围岩位移量大于传统方法,更接近于真实值,位移量随倾角变化规律与原先一致,且波动幅度更大,充分体现了层状围岩变形的倾角效应。此外,修正后位移量基本大于修正前,说明该方法能在一定程度上减小模拟值与实测值间的误差,但当岩层倾角超过60°后,该方法适用性有所降低。

2)对比发现,修正后各关键点处(σ1-σ3)值均大于修正前,说明参数修正法能进一步提高关键点处应力敏感度,为工程施工提供更加安全的保障。且修正前后(σ1-σ3)变化规律与修正前一致,均为先增后减再增。

3)修正前后围岩塑性区随倾角转动方向一致,进一步证明了该法的合理性。同时,当修正后岩体内摩擦角小于节理内摩擦角时,围岩塑性区面积较大;反之,当修正后岩体内摩擦角大于节理内摩擦角时,围岩塑性区面积较小。

4)通过对模拟时的岩体参数进行修正,能够在一定程度上减小模拟值与实测值间的误差,提高围岩数值模拟可靠度,为工程实际提供参考。

5)在后续的研究中,可进一步探索其他多种方式对岩体参数进行修正,并与瞬时等效修正进行对比,以模拟值和实测值间误差为依据,选取最佳修正方法并应用于实际工程研究当中。以倾角30°围岩为例,由位移分布图和塑性区图可知,隧道右拱肩和左拱脚相比其他位置更易出现破坏,符合工程背景所述隧道初支破坏情况。

综上所述,修正岩体强度参数法既能保证计算的正确性,同时其所得结果又更加接近真实值,对工程的设计和施工具有较好的指导意义。