结合加权引导滤波和小波变换的低照度图像增强算法
王少东,吴春林,刘永城,谢雨晴,王正家
(1 湖北工业大学机械工程学院, 湖北 武汉 430068; 2 湖北工业大学底特律绿色工业学院,湖北 武汉 430068)
车辆检测、行车记录和交通视频监控等场景都严重依赖高质量的图像[1]。但由于外界环境光线不足和光线照射不均匀等,导致采集到的图像亮度不高,信噪比偏低且图像纹理较少,这不但影响了人眼的视觉感官,也增加了图像中有效信息的使用难度。因此,需要合理增强低照度图像,使其具有较强的细节表现能力。当前常用的低照度图像增强算法主要包括直方图均衡化[2]、图像亮度反转去雾[3]、Retinex算法[4]、小波变换[5]和深度学习[6]等方法。直方图均衡化通过调整灰度值的分布概率进行增强,但容易造成灰度级减少和细节消失。王小元等[3]将低照度图像进行反转,使用去雾算法进行增强,但出现了过度增强的现象,造成图像模糊。Land 在1997年提出Retinex颜色恒常性理论。基于此理论,Jobson等[7]提出的单尺度Retinex(SSR)和多尺度Retinex(MSR)用于图像增强并取得一定效果,但增强后的图像存在颜色失真、噪声放大和 “光晕伪影”等现象。此后研究学者提出不同的改进增强算法。刘晓阳等[8]使用双边滤波进行照射分量估计以改善“光晕”现象,但由于双边滤波的特性,其算法的改善效果不够明显,且存在颜色失真现象。冯红波等[9]使用自适应因子,根据图像亮度选择不同高斯尺度的权重值,减少了增强后图像的颜色失真。肖创柏等[10]使用引导滤波作为环绕函数进行增强,图像具有一定边缘保持能力,但是在图像边缘处存在晕影,图像噪声也未得到抑制。使用深度学习的方法进行增强需要构造复杂的网络模型,而且模型的调整参数过多,训练复杂,设备的性能要求高[6]。
RGB颜色空间中色彩与各通道值紧密关联,直接对RGB图像处理容易导致颜色失真。传统使用高斯滤波的Retinex算法,不能准确地定位边缘,导致出现了“光晕”现象,增强后图像细节严重丢失,同时无法减少或抑制噪声。鉴于此,结合HSV空间中各通道互相独立的特性,本文提出结合加权引导滤波和小波变换的低照度图像增强算法,对V通道分量进行增强和去噪处理。实验数据表明,该算法有效增强了低照度图像亮度,色彩保真,细节较好,有效抑制了“光晕伪影”和噪声。
1 相关理论
1.1 HSV颜色空间
HSV颜色空间使用色调(H)、饱和度(S)和明度(V)表示图像。与RGB颜色空间不同,HSV颜色空间各通道互相独立,这种特性更接近人类对于色彩的感知。由于直接对RGB图像进行处理容易造成色调变化等问题,从而出现颜色失真的现象,本文首先将图像转换至HSV颜色空间处理,然后转换至RGB颜色空间输出增强的图像。HSV与RGB颜色空间的转换如下:
V=max
(1)
(2)
式中:r,g,b代表图像在RGB空间中三通道的像素值,max为(r,g,b)中的最大值,min为(r,g,b)中的最小值。
1.2 Retinex理论
Retinex理论是一种色彩恒常性理论,其认为物体表面的颜色不受外界环境光照变化影响,而是由其对光线的反射能力决定。该理论认为图像由两个分量组成,即
S(x,y)=R(x,y)L(x,y)
(4)
式中:x和y是图像中像素的坐标,R(x,y)为反射分量,L(x,y)为照射分量。
单尺度Retinex算法使用高斯滤波器估计照射分量,从而计算出反射分量
L(x,y)=G(x,y)*S(x,y)
(5)
式中:*为卷积运算符;G(x,y)一般选择为高斯滤波器,其定义为
(6)
其中δ为高斯尺度,C为调整因子,使得G(x,y)满足在高斯滤波尺度范围内对其积分的和为1。
将式(4)转换至对数域运算计算照射分量。
r(x,y)=lgR(x,y)=lgS(x,y)-lg(G(x,y)*S(x,y))
(7)
式中:r(x,y)为得到的反射分量,即增强后的图像。
多尺度Retinex(MSR)算法在单尺度Retinex算法基础上发展而来,其结合高、中、低3个尺度的滤波结果估计照射分量。
(8)
式中:K是中心环绕的个数,一般取K=3;ω1=ω2=ω3= 1/3。
2 算法
为解决低照度图像增强处理后图像色彩失真、图像细节差和“光晕伪影”现象等问题,根据HSV颜色空间各通道的独立性,提出结合加权引导滤波和小波变换的低照度图像增强算法。采用改进加权引导滤波作为环绕函数的多尺度Retinex算法和改进的阈值函数分别处理V分量小波分解的低频系数和高频系数,对小波逆变换重构的V分量进行Gamma校正处理以增强对比度;最后将H、S分量和增强后的V分量转换至RGB颜色空间。算法流程如图1所示。
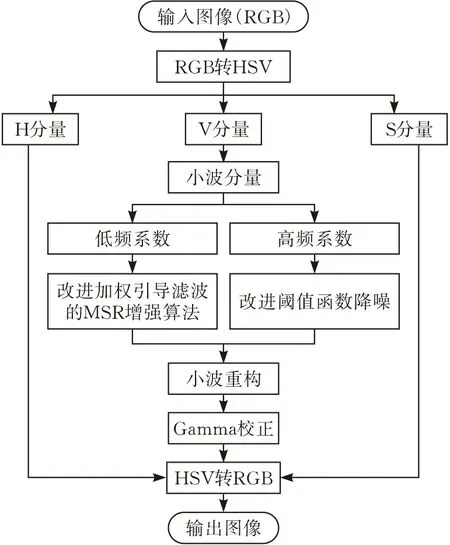
图1 本文算法流程
2.1 小波分解与重构
小波变换使用一系列的小波函数族表示某一信号,具有正交和双正交的特性。使用小波变换在对图像进行分解时,可以很好地消除图像中像素点间的相关性,有效提取高频系数和低频系数。
二维离散小波变换进行分解可实现图像全局信息与局部信息的分离,公式如下:
(9)
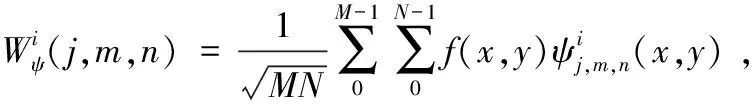
(10)

将增强处理后V分量高低频系数小波反变换重构:
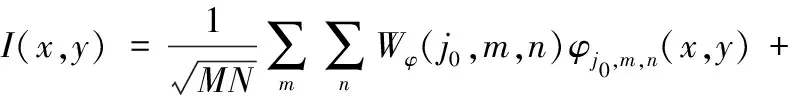
(11)
2.2 改进的多尺度Retinex算法
传统Retinex算法使用高斯滤波器作为环绕函数估计入射分量,这种估计来源于假设入射分量是在当前环境光照条件下的平滑图像。当图像中存在高对比度区域时,使用高斯滤波器估计出的入射分量仍为平滑图像,此时增强后图像的高对比度区域将产生“光晕”。同时由于高斯滤波器的低通特性,对图像的边缘保持能力不够,导致增强后图像的细节损失较多。
因此一些学者提出使用具有保边效果的滤波器,如双边滤波器和引导滤波器。引导滤波相较于双边滤波具有更好的边缘保持特性,且计算复杂度低。根据引导图像I的内容计算输入图像p经滤波后的输出图像。
qi=akIi+bk,∀i∈wk
(12)
式中:i和k为索引,wk为以K为中心的正方形窗口,引导图像I可以与滤波图像P相同。ak和bk是wk窗口中的常量。最小化q和p之间的差异,则在窗口中有代价函数:
(13)
式中ε为限制ak的正则化参数。通过线性回归求解:
(14)
(15)
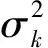
由式(14)可知在不同窗口中参数ε是固定不变的。在图像的边缘信息丰富的窗口,计算所得的线性系数ak较大需要对正则化参数ε进行惩罚。鉴于此,文献[11]提出一种结合方差加权的引导滤波算法[11]。该算法将窗口的局部区域方差作为权重因子,对固定的ε进行惩罚,得到自适应窗口的ε值,相较于原始的引导滤波法可以较好的保护边缘。但存在方差较大值的某些窗口不对应图像的边缘现象,所以用方差作为惩罚因子的方法有待改进。
本文对文献[11]中加权引导滤波的惩罚因子进行改进,采用局部高斯差分Dog(difference of gaussian)算子的对参数ε进行惩罚。重新定义滤波窗口wk中的权重因子如下:
(16)
式中:N为像素总数,Dog(i)是高斯差分算子,i为中心像素,γ取值为0.066。
则代价函数更改为:
(17)
为验证改进加权引导滤波的边缘保持效果,对图2a进行入射分量估计。明显可以看出改进的加权引导滤波器的细节保持能力最好,边缘清晰,相比之下高斯滤波和引导滤波的结果较为模糊。

图2 入射分量估计结果对比
本文采用改进的加权引导滤波取代高斯滤波进行入射分量估计,则改进的多尺度Retinex算法公式如下:
(18)
式中Gk(x,y)为改进的加权引导滤波。
2.3 改进的阈值函数小波高频系数去噪
小波分解V分量得到的高频系数中包含图像的细节轮廓信息和噪声[12],因此需要对噪声进行去除以提高增强后的图像质量。对噪声的去除算法需要设定一定的阈值,本文采用固定阈值法确定阈值。
(19)
式中:σ为噪声标准差,N为图像大小,median( )为中值函数,λ为阈值。
采用一种改进的三段式阈值函数进行高频系数去噪。
(20)
小波重构后得到的V通道图像亮度值较低,需进行调整提高图像亮度。本文使用Gamma校正进行亮度调整:
(21)
式中:γ为校正参数,且γ≥1,本文中取经验值2。
3 实验结果与讨论
实验选取6幅不同场景的低照度图像,分别用SSR算法、MSR 算法、文献[10]算法和本文所提算法进行处理,对处理结果使用主观评价和客观评价进行分析。实验环境为Visual Studio 2015,编程语言选用 C++,并基于OpenCV3.4.2版本进行开发。实验使用的PC配置如下:Windows10操作系统,处理器intel i5-5300U,主频2.3 GHz,内存8.0 GB,固态硬盘512 G。SSR算法的高斯尺度为80,MSR的高斯尺度为15、80和200。本文算法使用“sym4”小波基,滤波窗口为5、15和30。

图3 低照度图像增强结果对比
3.1 主观评价
图3中,第1列为不同场景下的低照度图像,包括普通低照度室外图像、光照不均匀图像和亮度极低的室内图像。第2列为SSR算法增强处理后的图像,SSR算法处理后的图像明显亮度偏高,同时在Image a、Image b、Image c、Image d和Image e中出现“光晕”,且图像整体区域颜色失真。第3列为MSR算法增强处理后的图像,图像整体偏灰亮度较低,增强后的Image d图像盘子的周围存在“光晕”,图像严重失真。第4列为文献[10]算法增强处理结果,图像较为清晰,有效避免了光晕现象,但是图像整体较暗,增强后的Image e图像在屋顶与天空处存在明显的过渡痕迹,图像的噪声较多。
第5列为本文算法处理结果。相较于其他算法,本文算法增强后的图像亮度适中,色彩鲜艳且图像细节明显,未出现“光晕”,增强效果好。
3.2 客观评价
主观评价是观察者的直接视觉感受,依赖于不同的评价标准或个人经验,缺乏一定的稳定性。客观评价采用一致的评价方法,结果具有较好的稳定性。本文采用均值、标准差信息熵和峰值信噪比对图像增强效果进行客观评价。灰度均值反映了图像的整体亮度,标准差反应了图像的对比度,信息熵表示图像包含的信息量,峰值信噪比反应处理后图像的质量。
选取图2中Image c和Image d两幅图不同算法的增强结果,使用上述指标对图像进行客观分析,结果如表1和表2所示。
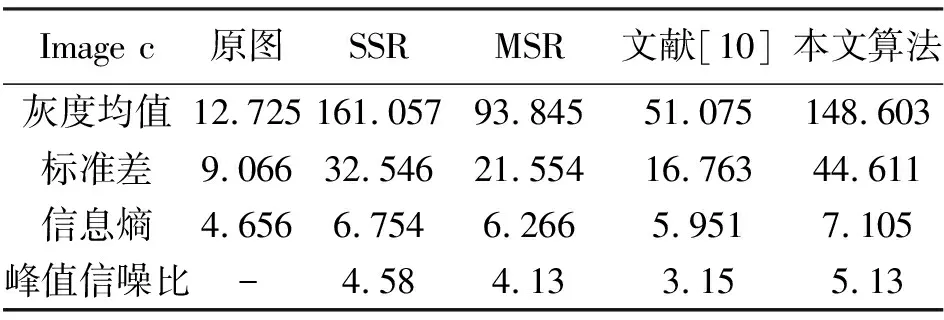
表1 image c图像增强评价数据
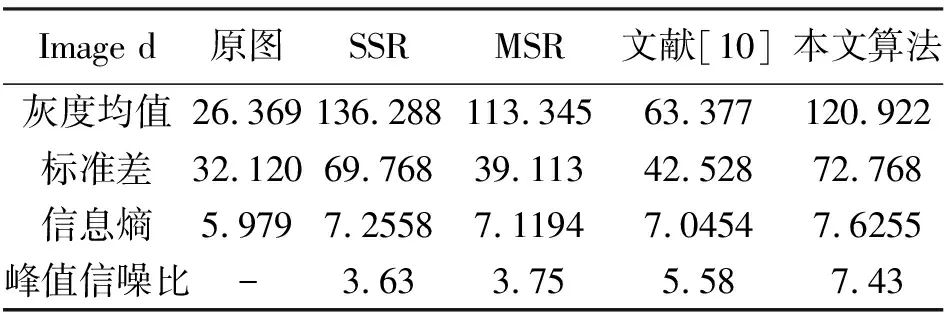
表2 image d图像增强评价数据
根据表1和表2中的评价数据可知,SSR算法增强的图像均值最高,但是图像整体偏白,图像细节模糊。本文算法处理后的图像亮度均值小于SSR算法的增强结果,但图像亮度适中,未出现图像增强过度的现象。本文算法的标准差高于其他算法,表明图像对比度高,细节表现能力强。另外,本文算法处理图像的峰值信噪比最高,色彩失真小,噪声得到了有效过滤。
4 总结
针对低照度图像增强处理后存在色彩失真、图像细节差和“光晕伪影”等问题,本文提出一种结合加权引导滤波和小波变换的低照度图像增强算法。增强后图像的主观和客观评价验证了本文算法可有效增强图像质量,消除了光晕伪影,同时图像细节表现能力较高,有效去除噪声。实验过程中发现本文算法对于部分低照度图像增强后灰度均值不高,在后续对此问题会做进一步研究。

