卷烟过滤嘴高精度多点实时温度测量

王选择, 尹晋平, 杨光远, 钱 虹, 王 娟

(1 湖北工业大学机械工程学院, 湖北 武汉 430068; 2 湖北中烟工业有限责任公司, 湖北 武汉 430040)

卷烟滤嘴去除烟气颗粒物的主要途径是惯性碰撞、扩散沉积和直接截留[1],而这些物理过滤效果与滤嘴的温度密切相关[2]。同时,滤嘴作为直接与吸烟者接触的部位,其温度高低直接影响了吸烟者的使用体验[3]。研究表明,滤嘴温度在抽吸结束前的2～3口高达70～80℃[4]。为了避免过高的滤嘴温度降低滤嘴对气溶胶颗粒物的截留效果,提高吸烟者对烟气感官质量的认可度,不少研究者通过改进滤嘴的内部材料来达到调控卷烟滤嘴温度的目的[3,5-7]。因此,随着消费者对卷烟质量的要求日益提高,各种采用新型材料的卷烟不断涌现,这使得滤嘴温度准确自动化检测在卷烟技术领域中的地位愈发重要。

在以往的研究中,研究人员更多关注于卷烟燃烧温度的测量及表征,主要采用热电偶、光导纤维、红外热成像及数值模拟来获取卷烟燃烧锥的温度分布[8-11]。然而,由于受到夹持及密封等条件的制约,卷烟滤嘴的温度测量存在着一定的困难。截至目前,滤嘴温度测量方法多数采用微细热电偶刺入卷烟滤嘴中以检测其内部温度[12-13]。而热电偶不仅灵敏度较低,容易受到外界干扰,且在刺入过程中容易折弯变形,导致定位精度不高,长时间使用易发生腐蚀与磨损,使之成为昂贵的消耗品。

为此,制做了内置NTC热敏电阻的专用烟支夹持器及其测量系统,旨在保证密封的前提下实现对ISO[14]抽吸模式下的卷烟滤嘴温度进行自动监测,揭示其温度变化及分布规律,并通过数学方法来表征滤嘴表面的温度分布。

1 检测原理

1.1 温度测量

NTC热敏电阻的基本温度测量电路如图1所示。图中,Vi为输入信号,Vo为输出信号,Rref为参考电阻,Rt为NTC热敏电阻。

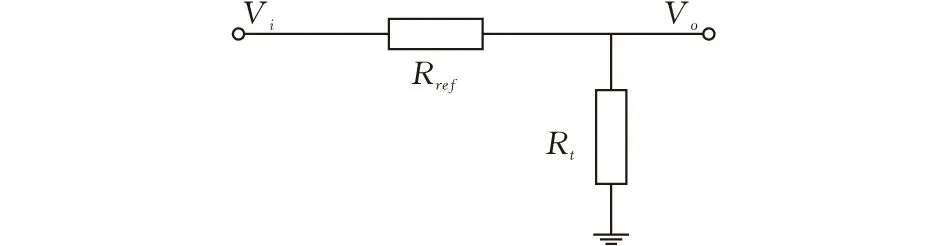
图1 NTC热敏电阻基本测温电路

根据串联分压原理,热敏电阻的阻值

(1)

显然,Rt的精度取决于Vo与Vi,因此要求准确获取Vo与Vi的值。采用交流调制激励的方式,可以尽量消除电源噪声与工频干扰等的影响,提高Vo与Vi的测量精度。

通过直接数字频率合成(DDS)方式产生的正弦交流信号[15],作为输入信号Vi,其幅值为Ai。对输入信号Vi与输出信号Vo通过同步模数转换器(ADC)进行采样,并利用数字正弦拟合处理采样数据以得到其幅值Ai与Ao。假设输入信号Vi与输出信号Vo可表示为:

(2)

式中:ω为角频率;φ1与φ2分别为输入信号与输出信号的初始相位,理论上有φ1=φ2。热敏电阻的阻值

(3)

利用NTC热敏电阻的阻值及其数学模型,即可推导出当前温度T。NTC热敏电阻与温度的关系为:

(4)

式中:R0为参考温度下的NTC热敏电阻阻值;T0为参考温度(一般选T0=298.15 K);Bn为由电阻材料决定的热敏指数。

1.2 交流信号处理方法

输入与输出信号通过ADC转换之后,均可获得一组相应的采样值序列Xn={x1,…,xi,…,xn},如图2所示。

图2 采样值序列

为准确获取它们的幅值信息Ai与Ao,采用最小二乘的正弦拟合方法[16]。序列中的任一值可表示为:

体育教学中应贯彻的教学原则有很多，但对于初中学生来说，最主要的就是要贯彻自觉积极性原则。即在发挥教师主导作用的前提下，只有最充分发挥学生主体作用，使学生由被动变为主动，由“要我练”转变为“我要练”，才能更好地提高体育锻炼的质量。

xi=Acos(Δi+φ)+C+εi

(5)

其中,Δi为累积相位,即序列中第i点与第1点之间的相位差。由于采样频率与信号频率都是已知量,故Δi也是已知量。令a=A·cosφ,b=-A·sinφ,则式(5)可进一步展开为:

xi=acosΔi+bsinΔi+C+εi

(6)

根据最小二乘线性正弦拟合[9],a与b可表示为:

(7)

1.3 温度预测算法

在被测介质温度连续变化时,尽管气流温度的变化可能较为迅速,但实际的温度曲线仍然是连续光滑的,且没有突变。为了消除温度测量时的随机误差,设计了一阶低通滤波算法。

低通滤波器的传递函数为:

(8)

其中,τ1为一阶滤波系统的时间常数。设滤波后温度为Tf,则有:

τ1·vTf+Tf=Ts

(9)

其中,vTf为Tf的速度。

为便于在嵌入式环境下计算处理,需进行离散化,并利用如下的递推公式,定义第i次的相关参数:

(10)

式中,ts为温度采样的时间间隔。通过设置vTf,0为0,并设置合适的τ1值,可以利用式(10)进行递推运算以完成温度数据的滤波。

进一步,在标准实验法获取温度传感时间常数τ2的基础上[7],结合一阶滤波的温度变化速度的计算结果,利用式(2)进行微分补偿,补偿结果可表示为:

Tp=Tf,i+τ2·vTf,i

(11)

值得说明的是,滤波时间常数τ1与温度传感时间常数τ2满足τ2>10τ1,保证在消去高频噪声的同时,准确预测真实温度。

2 试验方法

2.1 卷烟夹持与密封方法

为保证卷烟抽吸时可以被固定和防止漏气,本文采用自主设计的便于布置NTC热敏电阻的卷烟夹持器,其结构如图3所示。

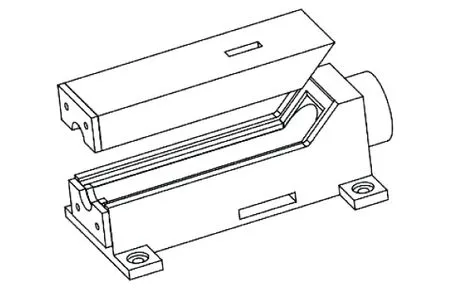
图3 卷烟夹持器

卷烟夹持器由上夹持片与下夹持片组成,下夹持片内边缘放置有异形密封圈。当卷烟滤嘴部分完全放入夹持器中后,上夹持片与下夹持片夹紧,并通过异形密封圈密封。同时,上下夹持片均预留有传感器引线出口供信号线引出,下夹持片右端设置有螺纹孔以便于连接气动快插气嘴。

2.2 测温点布置方法

利用17个NTC热敏电阻进行温度测量,在滤嘴的侧面布置4×4个测温点,在滤嘴的末端面布置1个测温点。同时,在滤嘴进气端使用插针式铂热电阻刺入内部以检测进气温度。据此,制做了如图4所示的侧边测温模块与端面测温模块。

在试验中,需将4个侧边测温模块平行于卷烟夹持器轴线均匀贴装在内壁,端面测温模块根据滤嘴长度垂直于卷烟夹持器轴线放入合适位置即可。最终测温点在卷烟滤嘴上的位置如图4所示。

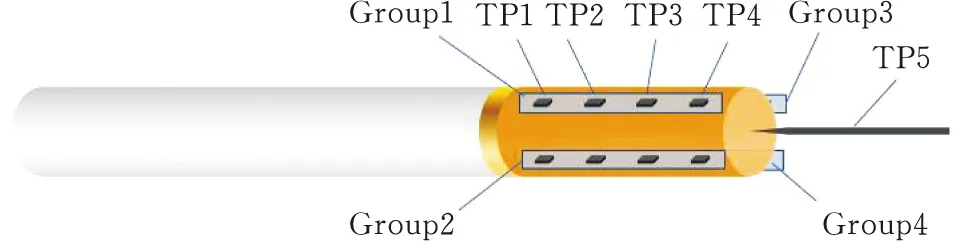
图4 测温点布置

3 实验结果

由STM32F407的DAC转换器产生的频率为5 kHz,直流偏置C= 1.25 V,幅值A= 610 mV的正弦输入信号Vi;输出信号Vo由STM32F407的ADC模块进行采集,采样频率为100 kHz。热敏电阻型号NCP15XH103F03RC,利用前述方法求得测量的初步温度数据,时间常数τ=1.04 s,ξ= 0.7,ωn=18。在27.2℃的环境温度条件下,以5 s的抽吸间隔进行抽吸测试,每次抽3 s,测试过程中持续监测抽吸时滤嘴表面的温度变化,以得出抽吸时的基本变化规律。图5为实验照片,整个采集系统集成在检测仪器内。

为了高精度地获取烟嘴的温度变化情况,首先利用所设计的温度传感方法对环境温度经过一段时间的采集,考察NTC温度传感分辨精度。

图5 燃烧烟温度测量实验

图6显示了7 min的温度采集曲线。虽然环境温度的波动一定程度上造成了0.03°C的漂移,但测量噪声控制在±0.01℃以内,说明所采用的交流调制方法具有较强的抗干扰能力,能够得到分辨精度达±0.01℃的测量水平,为烟嘴温度测量仪器的精确温度变化测量提供了较理想的测量方案。

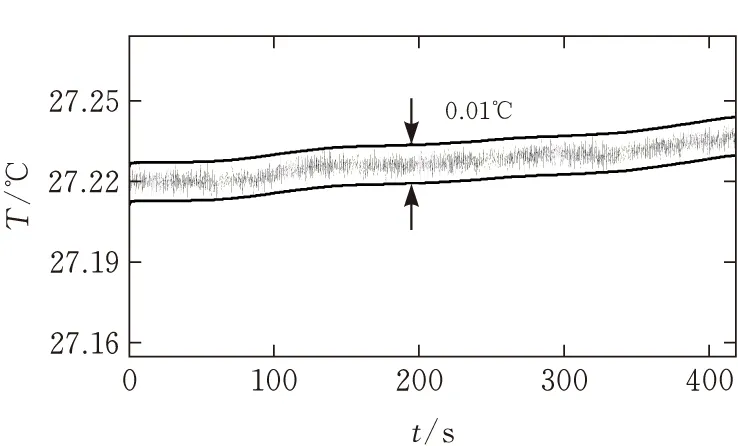
图6 重复测量数据

3.1 电子烤烟温度测量实验

电子烤烟滤嘴17个点10次抽吸的温度数据如表1所示,表中数据为每次抽吸的最高温度。图7为第1组(TP1,TP2,TP3,TP4)和第5组(TP5)中热敏电阻所测电子烤烟监视点的温度变化曲线。使用差分预测方法,控制采样时间小于50 ms。

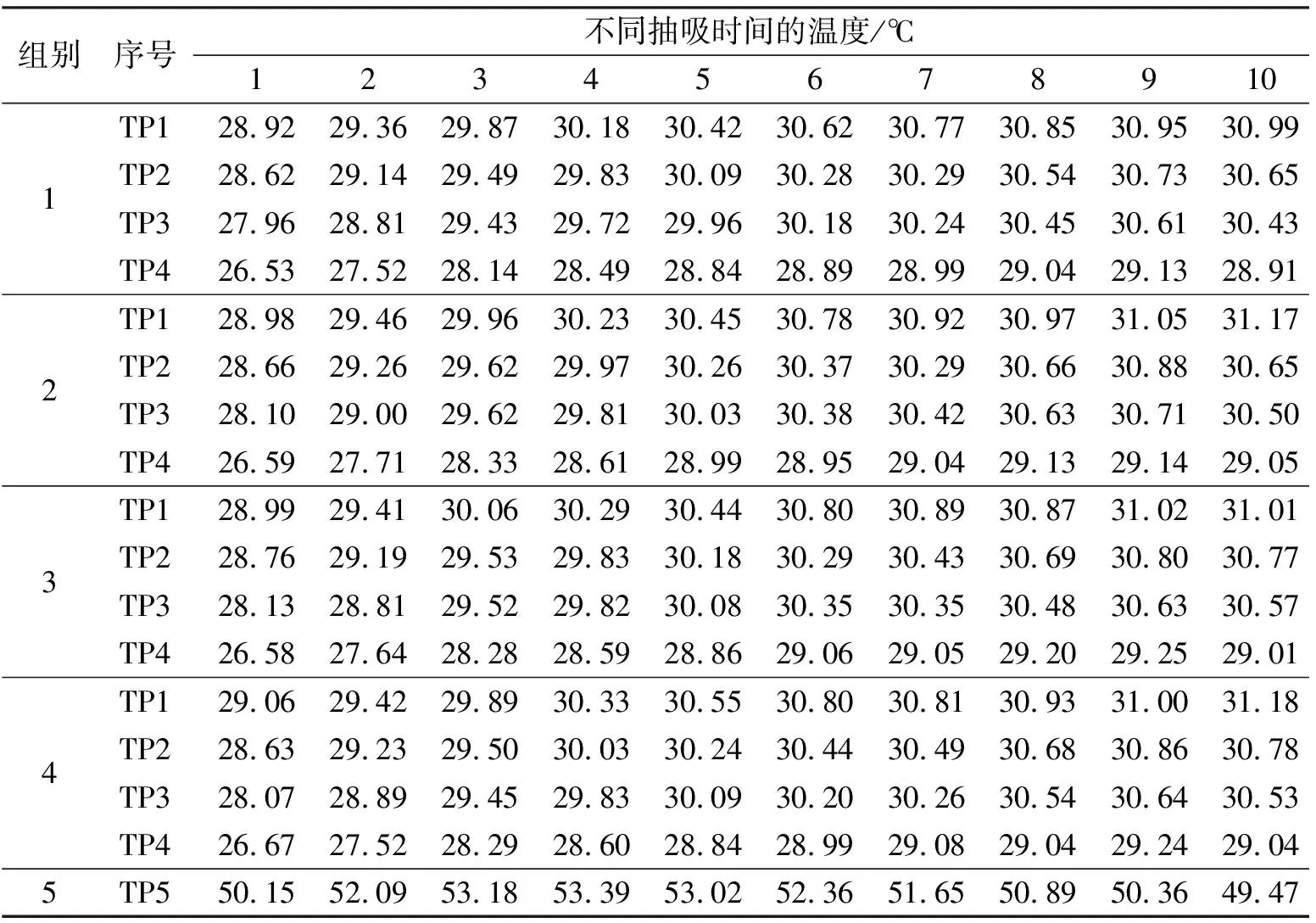
表1 燃烧烟多点温度测量结果

由图7可知,与燃烧烟端面温度缓慢升高的规律不同,用TP5测量的电子烤烟的端面温度在第1次抽吸时就很高;在吸气瞬间,电子烤烟端面温度同样会产生突变,停止抽吸时温度缓慢降低,但随着抽吸次数的增加,端面温度波动不大,在第4次抽吸时达到最大值。

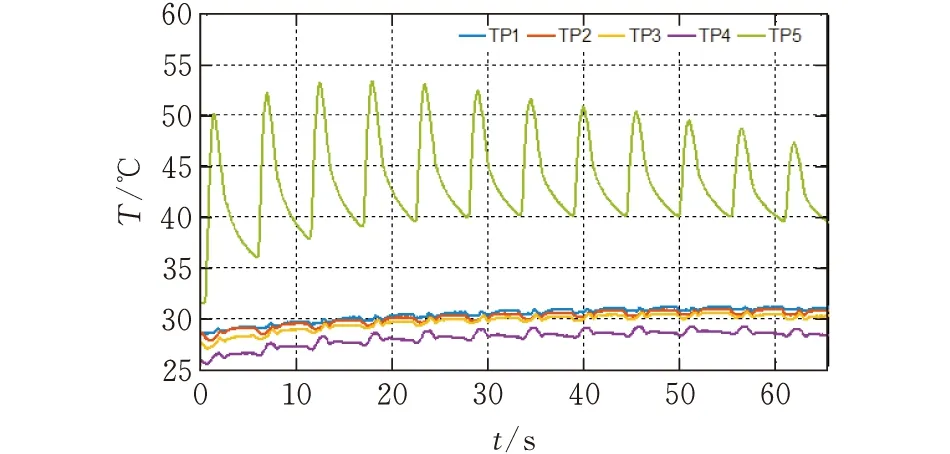
图7 电子烤烟不同监控点的温度变化曲线

图8为10次抽吸过程中4个不同组的相同圆周上传感器所测温度平均值曲线。由图7可知,TP1、TP2、TP3和TP4测得的温度变化缓慢,经过10次抽吸后仅上升了2℃左右,且 TP1和TP4之间存在2℃的温差。过滤嘴(TP5)端面的温度从50.15℃开始,在第4次抽吸时达到最大值53.39℃,然后缓慢降低。

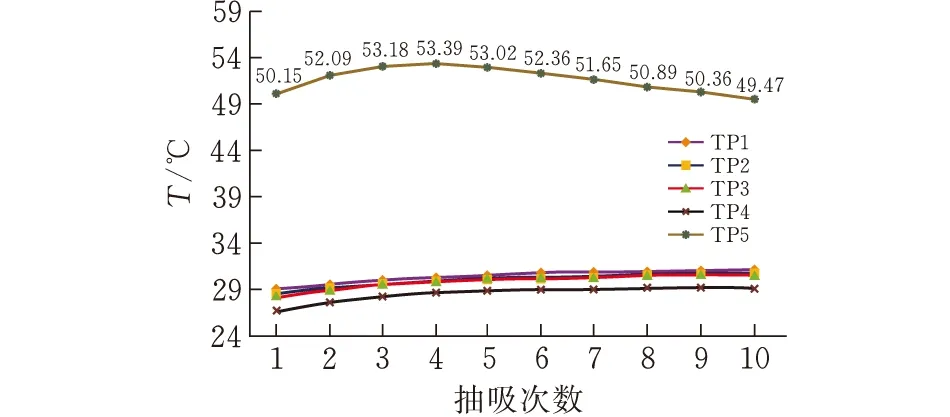
图8 电子烤烟不同监控点的温度变化曲线

由图8和图10可知,燃烧烟和电子烤烟的温度变化规律有较大差异,尤其体现在端面上。在燃烧烟中,端面温度从正常值33.55℃开始,并随着抽吸次数的增加而升高,最终达到最大值62.06℃;在电子烤烟中,端面温度始于较高值50.15℃,并随着抽吸次数的增加,其温度变化范围较小。

3.2 燃烧烟温度测量实验

用同样的方法对燃烧烟进行测量实验,10次抽吸过程中4个不同组的相同圆周上传感器所测温度平均值曲线如图9所示。由图9可知,TP1测得的远端温度比TP4测得的温度低4℃。过滤嘴四周温度随着抽吸次数的增加而缓慢上升,前6次抽吸温度上升较慢,后4次抽吸温度上升相对较快;抽吸10次后,相同圆周上的温度升高了9℃左右。TP5为滤嘴端面温度,由于烟气直接流过该传感器,因此温度比滤嘴四周要高,且变化较大,从第一次抽吸33.55℃到第10次抽吸62.06℃,温度上升约30℃。

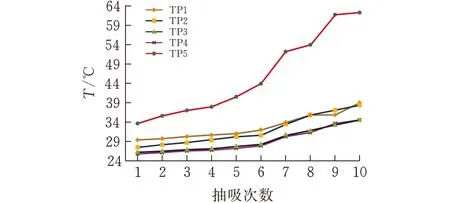
图9 燃烧烟不同监控点的温度变化曲线

4 结论

本文设计的测量系统使用17个NTC热敏电阻作为传感器,检测烟支过滤嘴17个点的温度。通过检测电路和差分预测方法保证测量结果的准确性和可靠性。分别对电子烤烟和燃烧烟进行了多点实时温度测量实验,验证了该方法的有效性。实验论证了两种香烟的温度变化规律:电子烤烟过滤嘴端面温度始于较高值50.15℃,但随着吸气次数的增加而平稳波动,其中在第4次抽吸时达到最大值。燃烧式香烟过滤嘴端面的温度随着抽吸次数的增加而逐渐升高,最高上升约30℃。在整个吸烟过程中,燃烧烟滤嘴四周的温度变化9℃左右,电子烤烟变化2℃左右。