基于多传感器的斜坡路面上自主跟随定位方法

陈长乐, 景嘉宝, 刘永城, 谢雨晴, 何 涛,

(1 湖北工业大学机械工程学院, 湖北 武汉 430068;2 湖北工业大学底特律绿色工业学院, 湖北 武汉 430068)

随着经济与科技快速发展,果实采摘机器人[1]、自动跟随行李箱[2]等自主跟随机器人的需求日益增多,应用也越发广泛。自主跟随机器人应用场景较为自由,环境复杂,因此对移动目标的准确定位是当前研究热点[3]。

目前定位方法主要分为视觉导航定位[4-5]、GPS导航定位[6]、超声波导航定位[7]。视觉导航定位通过识别图像特征实现定位,但图像算法复杂,且移动目标遇到遮挡物或环境光线过暗、过亮时,传感器难以识别目标。GPS导航定位通过终端芯片解算卫星坐标及距离实现定位,多用于户外空旷环境,如车辆路线规划、行人导航等,而室内环境容易出现GPS信号丢失问题。超声波导航定位通过解算发射至定位目标的回波时间实现定位,其具有不受环境光照干扰的优点,被广泛应用于自主跟随机器人的定位导航系统中。

超声波导航定位方法当前多使用三角定位法,如文献[8]和文献[9] 使用的多传感器信息融合分析计算出移动目标中心坐标。但当前方法都只适用于移动目标与跟随机器人在同一水平面情况。在斜坡路面,移动目标与自主跟随机器人之间出现水平高度差和俯仰角文题,会增大当前方法的定位精度,难以满足定位系统需求。

基于以上分析,本文提出了一种基于多传感器信息融合的自动跟随定位方法。该方法在自主跟随机器人上加装两个信号接收模块和角度测量模块。在移动目标上设置多信号源,同时加装陀螺仪用以检测移动目标本身前后倾角的改变,建立机器人与移动目标间的冗余信道;设定基于移动机器人的空间坐标系,考虑空间俯仰角的前提下使用三角定位法测量多个信号源的空间三维坐标;根据测量到的样本点坐标,利用最小二乘逼近[10]准确计算斜坡路面上移动目标中心坐标。

1 移动信号源定位方法

本文采用三角定位法定位移动信号源,定位原理如图1所示。

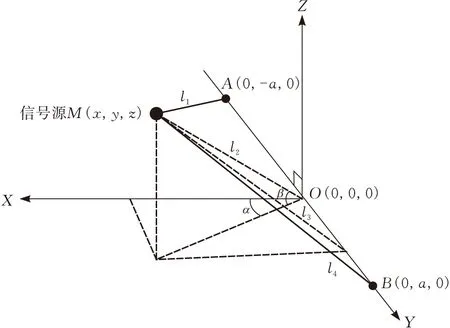
图1 信号源三角定位法

机器人上的对称信号节点A、B、O在平面的坐标分别为(0, -a, 0)、(0,a, 0)、(0, 0, 0),假设移动目标中心节点坐标为(x,y,z),测得信号源到A和B的距离为l1、l4,俯仰角为β。在移动目标与A、B两点构成的平面内,由几何关系可得出:

(1)

(2)

(3)

由式(1)、式(2)和式(3)可得:

(4)

(5)

在空间坐标中,根据几何关系可得:

(6)

z=l2·sinβ

(7)

由式(3)、式(4)、式(6)与式(7)可得:

(8)

(9)

2 多源信号定位模型及算法

2.1 移动目标多信号源定位模型

本文建立的定位模型在移动目标上将m个信号源以半径为R圆形排列,等距离布置,便于计算(图2)。在移动目标移动时,由于地面坡度的变化,信号源与跟随机器人之间产生俯仰角,移动目标本身的平面与信号源接收平面也会产生倾斜角θ(图3)。在计算过程中忽略俯仰角度会直接导致移动目标中心点定位计算不准确。因此在考虑移动目标相对于跟随机器人的俯仰角后,能够准确分析计算出坡面移动目标的移动方向和速度。

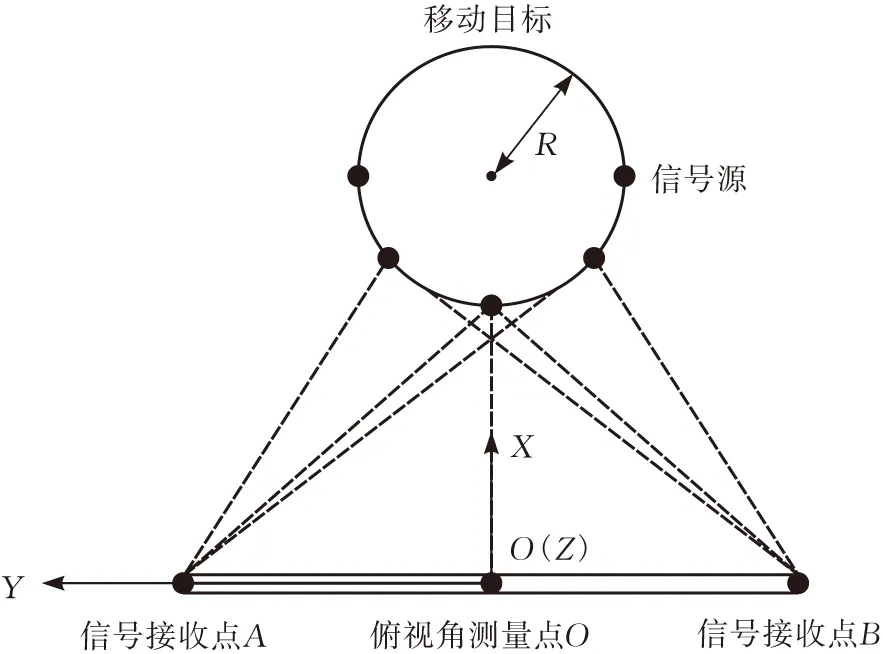
图2 多源信号定位模型

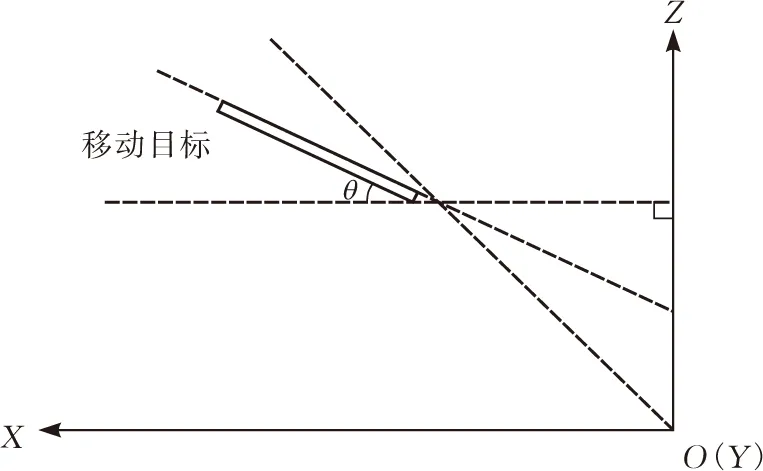
图3 坡面上的移动目标

移动目标在移动时,跟随机器人上的信号接收节点A、B以顺时针方向实时接收移动目标上的m个信号源的信号。角度测量模块O实时测量所有信号源的俯仰角。

将计算出的所有移动目标中心坐标使用最小二乘法逼近来得到准确的中心点空间坐标。由于移动物体保持着运动,每个扫描周期都会得出一个移动目标中心坐标,通过两个相邻周期得出的中心点坐标可计算出当前移动物体的运动方向和速度。

2.2 空间多信号源定位算法

为避免坡面倾角影响移动目标中心坐标、目标与跟随机器人O点的距离d、目标中心位置的俯仰角与方向角、移动目标的运动方向和速度,基于上述模型设计了结合俯仰角的空间多信号源定位算法。该方法结合多信号源的俯仰角来计算分析移动物体的运动方向和速度以及中心位置的特征数据。

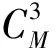
(10)

由式(10)计算可得:

A1x+B1y+C1z+D1=0

同理可得:

A2x+B2y+C2z+D2=0

A3x+B3y+C3z+D3=0

图4中So、Si、Sj和Sk分别是移动目标中心位置和任意已知的3个信号源位置。假设3个信号源确定的移动目标中心位置所在的空间圆半径为R0,由So、Si、Sj和Sk在空间中的几何关系可知:

(11)

获得Si、Sj和Sk3个信号源在空间中关于圆心空间坐标的线性代数方程组后解得

(12)

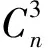
图4 中心坐标So计算模型

(13)

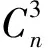
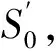
(14)

方向角

(15)

由式(14)和式(15)可计算得到移动目标中心位置的方向角和移动速度,其中方向角α和俯仰角β共同决定移动目标中心位置在空间中相对于移动机器人的运动方向。

3 移动目标定位实验

定位系统需求参数如图5所示,其中:移动目标定位检测距离L的范围需求为300～1500 mm;水平夹角γ需求为45°～135°,用于防止目标转向速度过快定位系统丢失目标;俯仰角β需求为-60°～60°,用于定位坡面移动目标;移动目标中心点坐标定位精度需求为X轴±50 mm、Y轴±50 mm、Z轴±50 mm。

图5 定位系统需求参数示意图

基于以上需求,本文设计了定位系统用于定位实验。在该系统中,选用了15个超声波传感器以24°间隔角在移动目标上以150 mm为半径的圆上均匀分布安装(超声波传感器测距范围在500 mm到4500 mm范围,测距精度为5 mm),移动机器人中心位置O设置两个超声波接收模块于z轴方向上,上下距离为50 mm,用于同时接收移动目标上某一信号源信号,测出该信号源离2个超声波接收模块距离以算出俯仰角;移动机器人左右各安装一个超声波接收模块,位于O点位置左右各250 mm,用于接收移动目标上的15个信号源信号。

为满足系统各参数需求,定位实验选择俯仰角β为60°的坡度进行实验。每次实验以移动目标相距跟随机器人水平角夹为γ、距离为500 mm处为起始位置,在坡度上每移动100 mm记录1次坐标数据,记录至1500 mm处停止。由于定位系统对称布置超声波接收模块,水平夹角γ为45°～90°,满足定位精度要求证明90°～135°的水平夹角也满足,基于此设置水平夹角γ为45°、60°、75°、90°共4组实验,验证本文设计的定位系统的有效性。

不同水平夹角下的坡面目标定位实验中,移动目标中心坐标定位误差见表1。分析实验数据可知,相比于传统移动目标定位方法容易丢失坡面移动目标,本文方法在满足检测距离、水平夹角的情况下,能够对处于60°坡度的移动目标进行有效定位,且目标中心坐标各轴测量误差处于±50 mm内,满足定位精度需求。其中,水平夹角为90°、检测距离为600 mm内时,本文方法检测精度最佳,目标中心坐标各轴定位精度±10 mm。对于实验测得移动目标中心坐标误差波动较大问题,经研究分析,与传感器标定精度相关,在对传感器有效标定后,本文方法可进一步提高对斜坡路面移动目标定位精度。

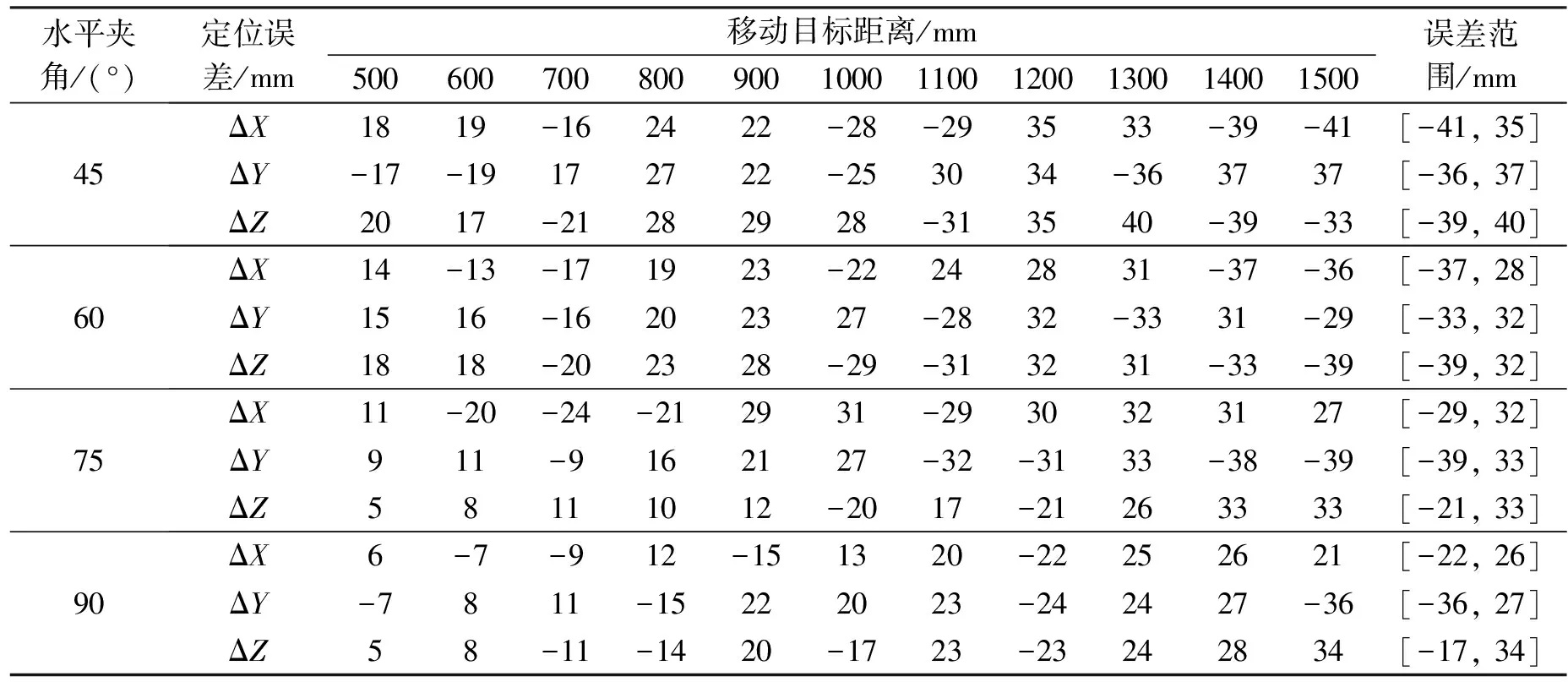
表1 移动目标中心坐标定位误差

4 结论

本文设计的坡度路面移动目标定位跟随方法,在机器人跟随目标时保证定位系统对坡度路面上的移动目标有效定位,避免因为坡度变化导致移动目标中心位置定位偏差,而偏差累积造成移动目标位置丢失问题。实验表明,该定位方法能够在具有坡度的路面上保证自动跟随机器人对移动目标的精准定位,有效降低了坡度对于定位精度的影响,具有一定的工程应用价值。