基于SWAT模型的气候变化条件下诺敏河流域径流变化研究

汪 飞, 洪 林, 马田遥, 吐尼亚孜, 熊继东

(1.武汉大学 水利水电学院, 武汉 430072; 2.余姚市水利局,浙江 宁波 315400; 3.宁波兴晟新能源科技有限公司, 浙江 宁波 315400)

近年来,气候变化及其影响引起了越来越多国内外专家学者的关注和研究[1-2]。IPCC第五次研究报告指出[3],地表温度因受温室气体浓度增加而持续升高,降水量、降水强度和降水时空分布也将发生改变,从而导致水资源分布及循环发生相应变化。气候变化提升了极端水文事件的发生概率[4],也会对区域径流的时空特性产生不同效应[5]。诺敏河流域位于我国东北部地区,近年来在以气候变化为主的环境变化因素影响下,流域内水资源趋向不足,水土资源的不协调也逐渐突出。因此,研究气候变化对诺敏河流域径流的影响,不仅能深入了解气候变化条件下径流的演变规律,也可为流域水资源的综合管理提供参考依据。

耦合全球气候模式与水文模型是研究气候变化对径流影响的主要方法之一[5-7]。刘春蓁等[8]采用4种GCM情景模式研究了我国7大流域径流和蒸发的变化可能性,并得出4种模式下松花江流域径流趋于增加;郭生练等[9]选用BCC-CSM1-1气候模式及RCP4.5排放情景,预测了长江流域气温、降水以及径流的变化情况;江介伦等[10]结合GWLF水文模型分析了5种大气环流模式下未来气候对径流的影响,发现丰水期水量上升而枯水期水量减小。以上研究虽然对径流受气候变化的影响进行了一些探究,着重得到未来气候变化条件下径流量的变化范围,但并未探究径流的突变、周期等特征。本文选取诺敏河流域作为研究对象,采用SDSM统计降尺度方法,借助大气环流模式预测流域未来的气候变化,并通过分布式水文模型SWAT模型模拟在未来气候情景下径流的相应特征。

1 研究区概况

诺敏河流域位于大兴安岭东南山麓,在121°45′—124°35′E,48°00′—50°30′N范围内,流域面积25 098 km2。流域平均海拔1 102 m,最高处可达1 300 m,河口高程最低约为170 m。流域春季干旱多风,夏季热而湿,秋季较短,冬季寒冷漫长,历年最高气温曾高达40.1℃,最低气温达到-35.4℃。诺敏河流域降水年内分配不均,雨量多集中在7—8月。流域总出口水文测站为小二沟站,控制面积占流域总面积的95%以上。

2 研究方法

2.1 趋势分析

趋势特征通常使用线性回归、斯皮尔曼分析法[11]、M-K检验法等[12]。本文以线性回归为主要的研究方式,并将突变分析时使用的M-K法作为补充。

该方法主要反映自变量和因变量的线性相关关系,公式如下:

Y=a+bX

(1)

式中:X为自变量,此处表示年份;Y为因变量,在本文中表示研究对象,如气温、降水、径流;a,b分别为回归系数,其值通过最小二乘法求得。

在趋势分析中,需要对研究对象和时间的相关性进行显著性检验,此处采用F检验法,统计量F的计算公式为:

(2)

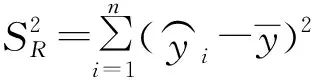
2.2 突变分析

突变分析采用在水文、气象等长时间序列的突变识别中应用较为广泛的M-K突变检验法[13-16]。

对于样本长度为n的长序列X,构造的M-K检验秩序列如公式(3)—(4)所示:

(3)

(4)

由于时间序列相互独立,定义新的统计量:

(5)

式中:E(Sk)为累计数Sk的均值;var(Sk)为Sk的方差。

其中,UF1=0,UFk统计量服从标准正态分布。查阅特征值表来得到给定的显著性水平α(本文采用α=0.05)所对应的临界值UFα,如果统计量大于临界值,则表明该序列存在着明显的增加、减少的趋势,从而判断时间序列是否存在趋势变化特征,作为趋势分析的补充。

E(Sk),var(Sk)的计算公式如下:

(6)

(7)

按照时间序列逆序编排,用上述的构造过程构造新的统计序列UBk。绘制UBk和UBk两条曲线图,若UFk和UBk相交,且交点处的统计值在检验的上、下置信度区间内,可认为交点所对应的节点可能就是突变发生的时间点。

2.3 周期分析

周期特征通常采用Morlet小波分析法,Morlet小波可以凸显长序列存在的周期特征,同时能够定性地评估序列未来的变化趋势。

其基本原理是由一组小波函数基来近似地表示所研究的特定函数,通过小波变化计算得到小波系数,再由小波系数的实部、模值等系列数值来分析时间序列中的变化特征。

(1) 小波函数。小波分析中需要构建震荡变化且最终能快速衰减到0的小波函数Ψ(t)∈L2(R),该函数需满足:

(8)

式中:Ψ(t)∈L2(R)为基小波函数,该函数经由尺度伸缩及时间轴平移形成子小波函数系:

(9)

式中:Ψa,b(t)为子小波;a为尺度因子,且a≠0,指小波周期的长度;b为平移因子,指时间轴上的平移。

(2) 小波变换。在小波变换中,分别在时间和频率两个尺度上分析一维序列的信息。对于已知的能量有限信号f(t)∈L2(R),子小波Ψa,b(t)的连续小波变换为:

(10)

式中:Wf(a,b)为小波变换系数;f(t)为平方可积函数。

由于获得的数据是离散的,假定函数f(kΔt),(k=1,2,…,N;Δt为取样间隔),那么离散的小波变换形式为:

(11)

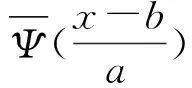
由公式(11)可知,小波分析借由增减伸缩因子来获得序列的低频和高频信息,进而得到不同时间、空间尺度层面的局部变化特征。

(3) 小波方差。小波方差是将小波系数值取平方,并在整个时间轴领域内积分,如公式(12)所示:

(12)

在不同的时间尺度下绘制小波方差变化过程,形成小波方差图,它能够体现信号波动过程中的能量汇集情况,从而凸显出序列中扰动剧烈的信息,分析判断主周期。

虽然至今未中过一毛钱，我的情绪倒也没什么大的起伏。毕竟只是动动手指，也没付出多大成本。只是成功塑造了一个价格敏感型消费者（穷鬼）的形象而已。

3 SWAT模型构建

SWAT模型是由美国农业研究所开发的适用于流域尺度的半分布式水文模型[17],包含气候、水文、侵蚀、土地覆盖变化、管理措施、主河道变化、营养物质和水体运动等多个部分[18-21],能够模拟流域内多种不同的水文循环过程[22]。模型具有很好的适用性,可基于GIS提供的空间数据,模拟长时间段内水文过程,被广泛用于不同区域变化环境下的流域水文特征研究[23]。

3.1 数据资料

本文选取诺敏河流域的小二沟站作为水文代表站点,选取流域内的8个气象站点作为研究对象。SWAT模型所需基础资料及来源见表1,各站点分布如图1所示。

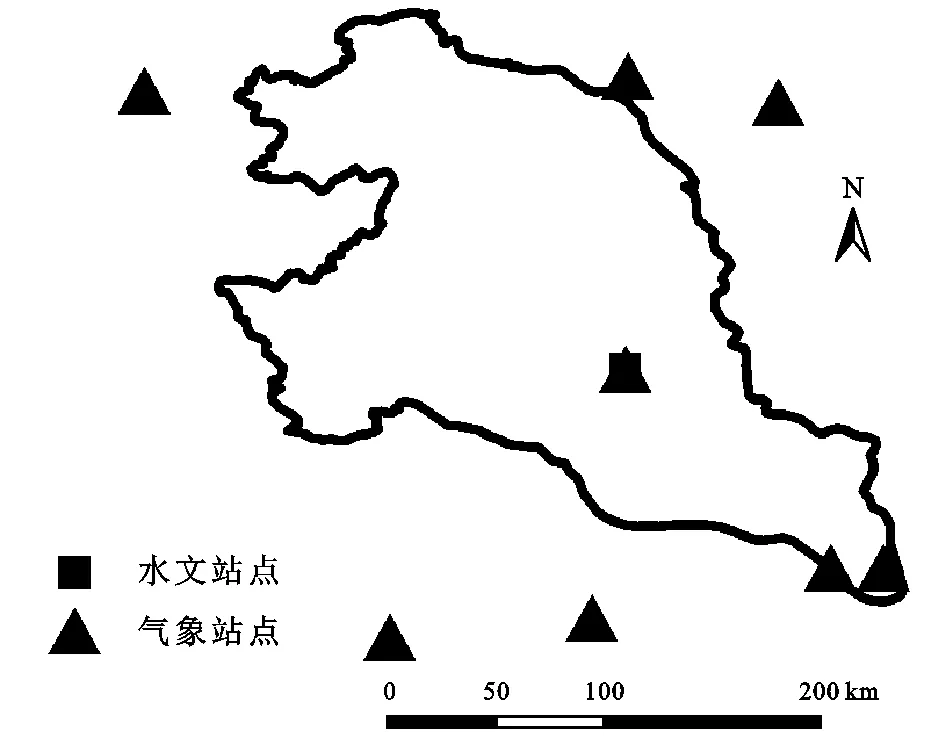
图1 诺敏河流域气象、水文站点分布Fig. 1 Distribution of meteorological and hydrological stations in Nomin River Basin

表1 诺敏河流域基础数据信息Table 1 Basic data information of Nomin River Basin

3.2 基础数据库构建

3.2.1 土壤数据库 本文使用FAO土壤数据库直接建立用户数据库[16]。模型所需的土壤物理属性参数按获取方式分为两部分:第1部分可直接从FAO土壤数据库中查取;其余数据通过SPAW软件和统计分析方法计算得出[24]。

3.2.2 土地利用数据库 将SWAT模型中定义使用的土地利用分布类型按照植被覆盖特征进行二级分类。对于不同的土地利用类型,考虑到属性表中有十几种类型,且其中有些类型可以合并为一种,因此先将它们进行重新分类,然后再得到能够直接使用的土地利用数据。

3.2.3 气象数据库 按照模型所需的格式要求,对各站点日值气象数据进行整理,并计算特征值,将结果录入SWAT模型的基础数据库中。

3.2.4 空间离散数据库 SWAT模型基于流域DEM提取河网水系并进行子流域划分,再根据不同的土地使用类型、土壤类型和坡度,将具有相同类型的单元进行归集,将诺敏河流域划分成273个水文响应单元。

3.3 模型参数率定与验证

选用决定系数R2以及纳什系数Ens来对SWAT模型的拟合效果进行评价,其计算公式为公式(13)—(14)。模型误差评价参考表见表2。径流拟合曲线见图2—3。

图2 小二沟站率定期(2006-2010年)年日径流拟合曲线Fig. 2 Fitting curve of annual daily runoff at Xiaoergou station from 2006 to 2010

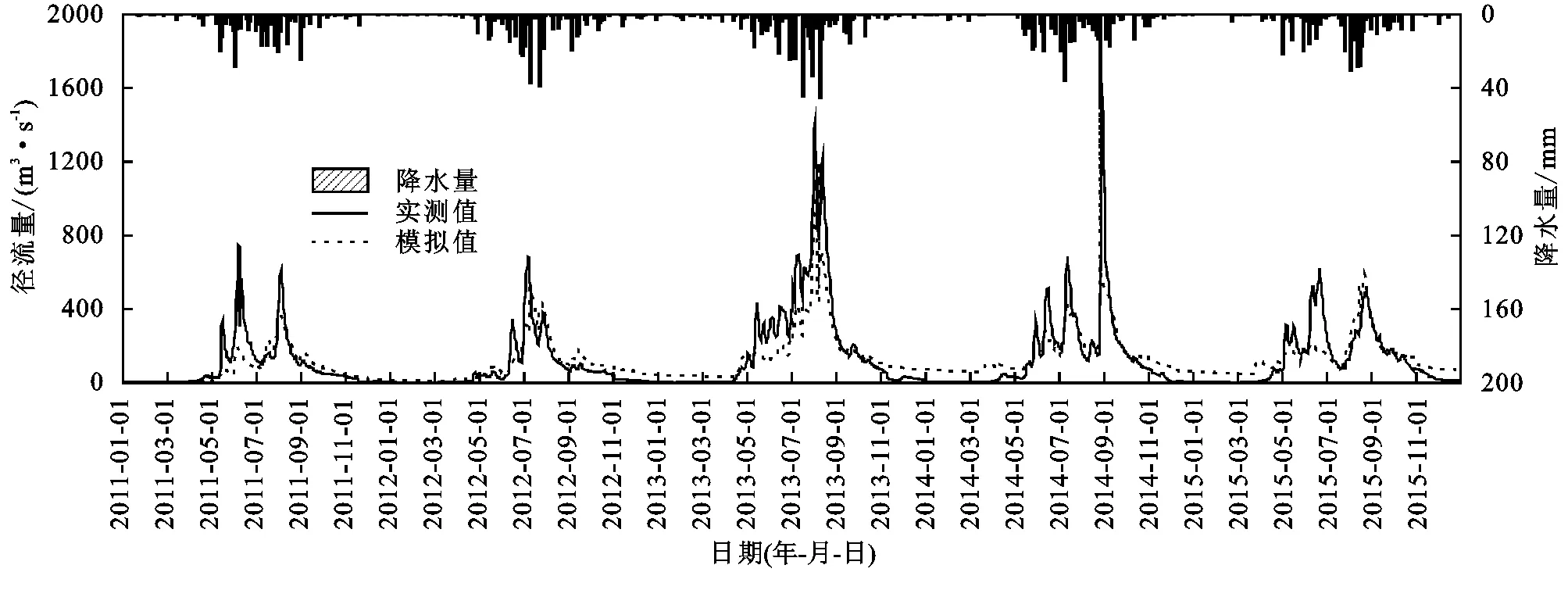
图3 小二沟站验证期(2011-2015年)年日径流拟合曲线Fig. 3 Fitting curve of annual daily runoff at Xiaoergou station from 2011 to 2015

表2 模型误差评价Table 2 Model error evaluation

(13)

(14)

从径流拟合曲线来看,径流模拟值和实测值趋势一致,两条曲线较为贴合。率定期和验证期的R2分别为0.76,0.73,Ens分别为0.72,0.70,两者的模拟效果都表现为良好。因此,径流的模拟能够满足模型所需的精度要求,故可以选用调整后的敏感参数值来进行后续的径流模拟,调整后的敏感参数见表3。

表3 SWAT模型敏感参数率定结果Table 3 Sensitivity parameter calibration results of SWAT model

4 未来情景模式下径流变化规律分析

对诺敏河流域而言,气温和降水是影响径流变化的最直接、最重要的气候因素。本文选择较常用、在我国东北地区适应性强的CanESM 5大气环流模式,采用SDSM统计降尺度对不同排放情景模式进行统计降尺度,获得诺敏河流域未来几十年的气象要素序列值,并将其输入率定后的SWAT模型,模拟研究区域径流对气候变化的响应,并分析径流的趋势、突变及周期变化特征。

4.1 气候情景设定

为模拟评估未来气候变化,IPCC第五次评估报告采用CMIP 5中的气候模式,预设了温室气体排放浓度情景(RCPs)。

其中:RCP2.6情景假设全球能源使用发生改变,温室气体排放将显著减少;RCP4.5情景假设可再生能源和碳捕捉系统广泛使用、森林储碳量增加,温室气体排放量也将显著减少;RCP8.5情景假设无政策干预,全球人口大幅增加、化石燃料消耗变大,温室气体排放和浓度不断增加。

本文使用CMIP 5中CGCMs模式的数据集CanESM5。该数据集包含了全球的历史数据集和全球2006—2100年RCP2.6,RCP4.5和RCP8.5三种情景下的基础数据。

4.2 气候要素分析

将大气环流模式中的未来数据统计降尺度,生成3种排放情景模式下的数据。对2021—2100年进行分析,设定2021—2060年为21世纪中期,2061—2100年为21世纪后期。

4.2.1 气温变化趋势分析 绘制3种模式下气温的趋势变化图并统计其特征值(图4、表4),3种情景模式下年均气温、年平均最高气温和年平均最低气温都保持增长的趋势。对比21世纪中、后期3种气温变化趋势可发现,随着时间的持续,3种排放导致的气候变暖结果差距将越来越大,尤其对于RCP8.5模式,整个21世纪都保持很高的增长率,增幅几乎都在0.65℃/10 a以上。对于RCP2.6和RCP4.5模式,气候变暖得到了有效控制,虽也呈现一定的增幅,但增幅明显小于RCP8.5模式,增长速率仅为RCP8.5模式下的1/4～1/2。两者相比较来看,对于21世纪中期,RCP2.6模式下多年平均气温稍高于RCP4.5模式,但相差不大;而对于21世纪后期,RCP2.6模式对气候变暖效果的控制要好于RCP4.5模式。

图4 诺敏河流域21世纪中期和后期3种排放情景模式气温变化趋势Fig. 4 Temperature change trends of three emission scenario modes in Nomin River Basin in the mid 21st century and late 21st century

4.2.2 降水变化趋势分析 绘制3种模式下年降水的趋势图并统计特征值。由图5、表5可知,3种情景模式下年降水都保持增长的趋势。其中,RCP8.5模式下降水的增幅最大,在21世纪后期增幅已经超过20 mm/10 a。对于RCP4.5模式,在21世纪中期,年降水的增幅为6.05 mm/10 a,到了21世纪后期,降水增幅增大至12 mm/10 a。RCP2.6模式下,降水增幅相对较小,且21世纪后期与中期相近,增幅相比另两种情景模式有所减缓。

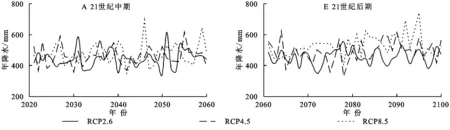
图5 诺敏河流域21世纪中期和后期3种排放情景模式降水变化趋势Fig. 5 Precipitation change trends of three emission scenario modes in Nomin River Basin in the mid 21st century and late 21st century

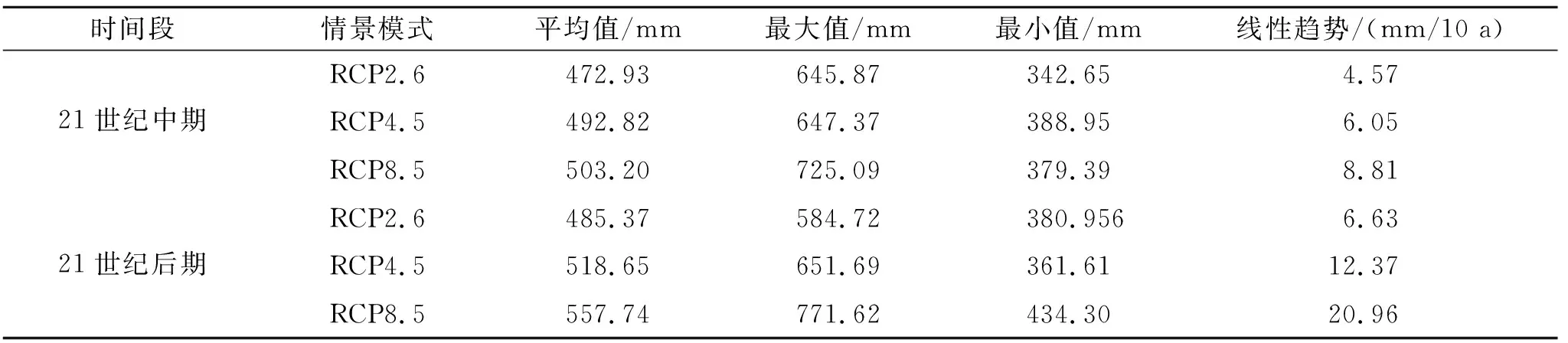
表5 诺敏河流域3种排放情景模式年降水特征值Table 5 Annual precipitation characteristic values of three emission scenario modes in Nomin River Basin

4.3 径流变化特征分析

4.3.1 径流趋势特征分析 绘制3种排放情景模式下年径流的趋势变化图并统计特征值(图6、表6)。结果显示:3种情景模式下径流都保持增长趋势。

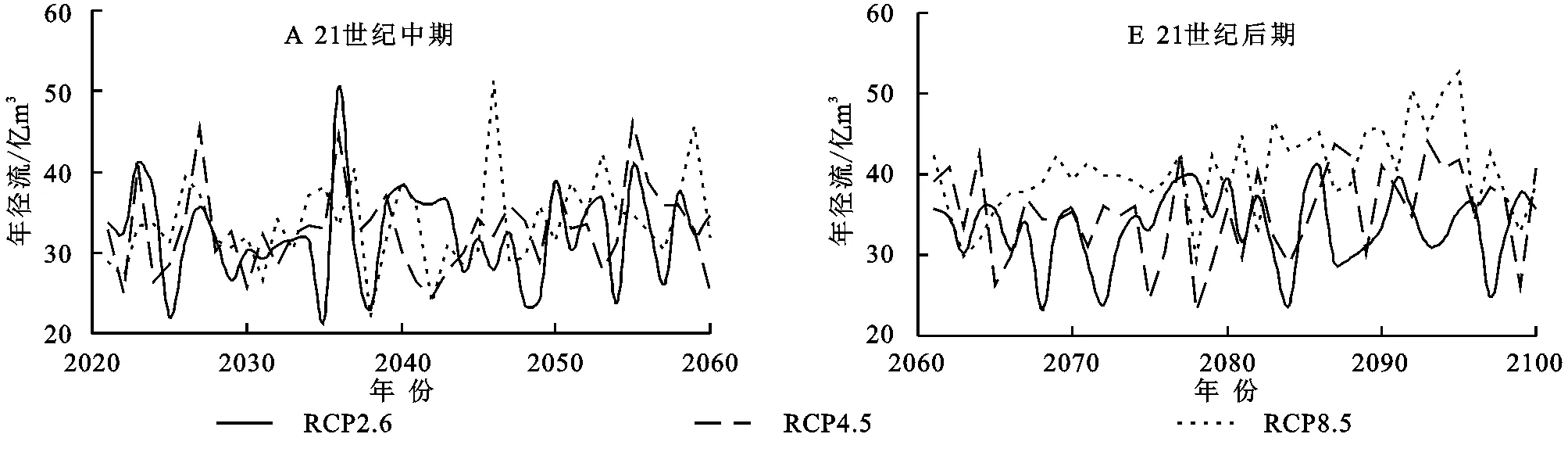
图6 诺敏河流域21世纪中期和后期3种排放情景模式下径流变化趋势Fig. 6 Runoff variation trend of three emission scenario modes in Nomin River Basin in the mid 21st century and late 21st century

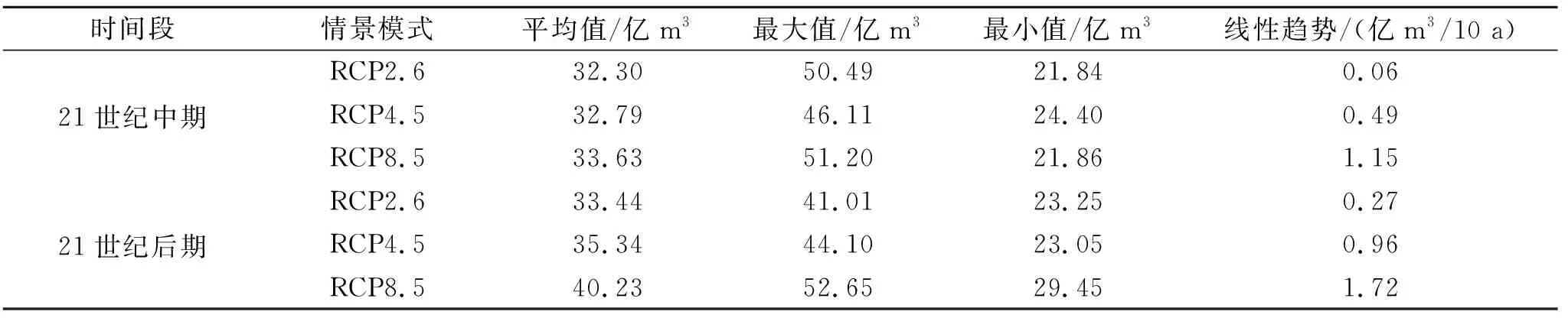
表6 诺敏河流域3种排放情景模式下年径流特征值Table 6 Annual runoff characteristic values under three emission scenario modes in Nomin River Basin

其中,RCP8.5模式下径流增幅最大,在21世纪中期保持1.15亿m3/10 a的增速,后期以1.72亿m3/10 a增长,因此到21世纪后期,其多年平均年径流量也最大,达到40.23亿m3。RCP4.5模式其次,在21世纪中、后期分别以每10年0.49亿m3,0.96亿m3的增速增长,到21世纪后期多年平均径量达到35.34亿m3。RCP2.6模式下径流量增长相对较少,在21世纪中期和后期增长量仅为每10年0.06亿m3,0.27亿m3。

径流的增长特征与流域未来的降雨和气温关系密切,一方面,降水增加对径流有着最直接的影响,径流随着降水的增加而增加;另一方面可以看到,RCP8.5模式下,21世纪后期降雨增加值非常大,为21世纪中期的3倍,而21世纪后期的径流增幅仅为中期的1.5倍,同样地,RCP4.5模式和RCP2.6模式下,降雨增幅分别为2,1.5倍,而径流增幅则分别为2倍和4倍。这是由于气温升高引起蒸散发增加,进而抑制了降水促进径流增加的作用。

4.3.2 径流突变特征分析 绘制3种情景模式下2021—2100年诺敏河流域径流的突变检验曲线(图7—9)。结果显示:随着气候变化,3种情景模式的径流突变特征产生了很大的差别。

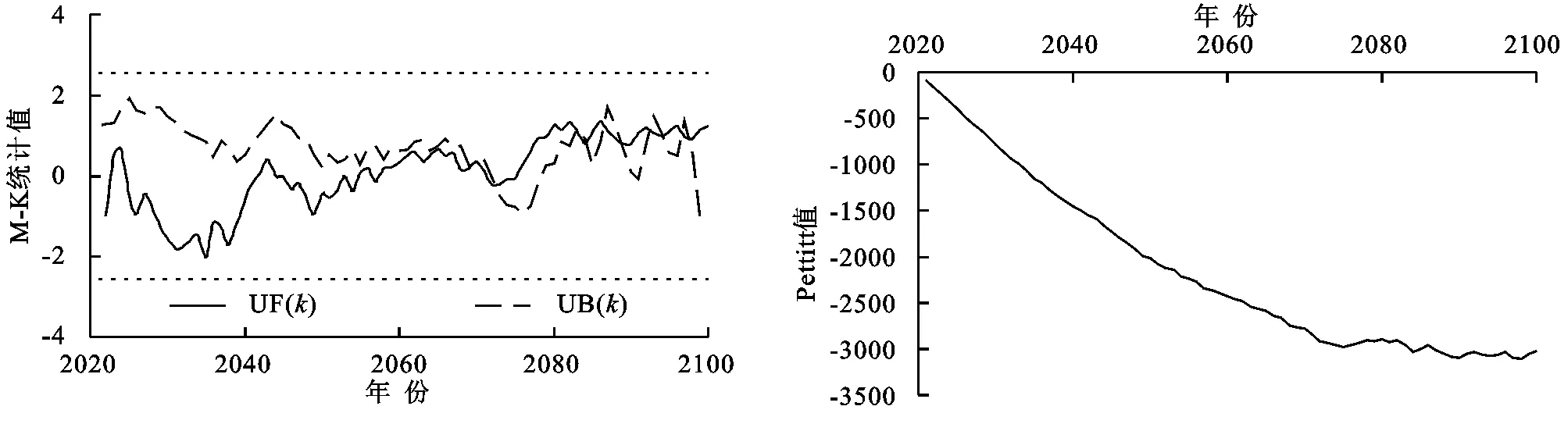
图7 诺敏河流域RCP2.6模式下径流M-K法突变识别、Pettitt法突变识别Fig. 7 Runoff M-K and Pettitt method mutation identification under RCP2.6 mode in Nomin River Basin

图8 诺敏河流域RCP4.5模式下径流M-K法突变识别、Pettitt法突变识别Fig. 8 Runoff M-K and Pettitt method mutation identification under RCP4.5 mode in Nomin River Basin

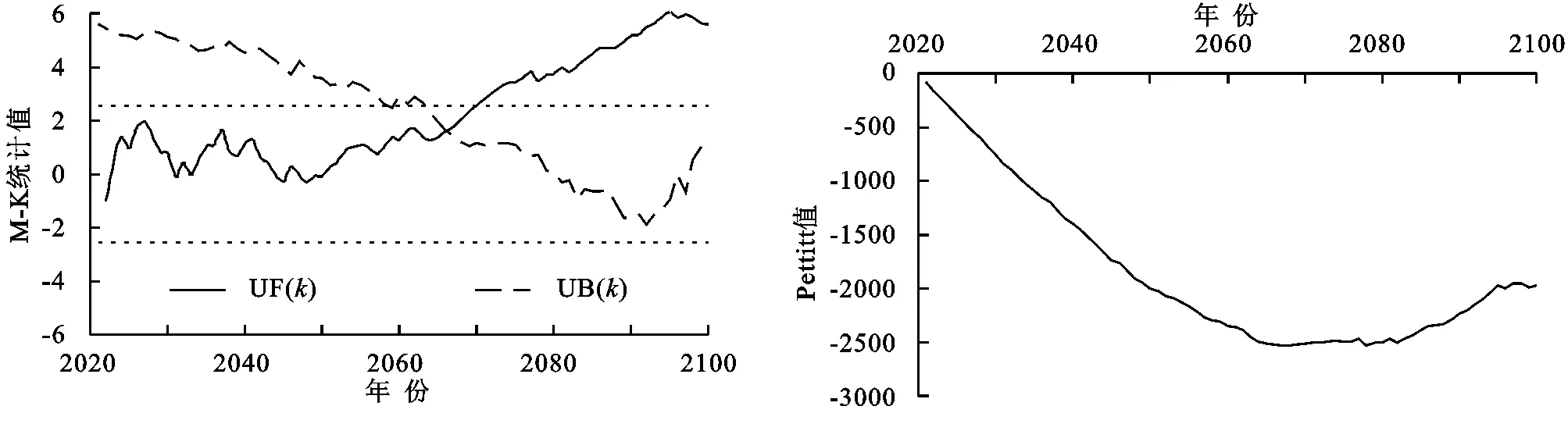
图9 诺敏河流域RCP8.5模式下径流M-K法突变识别、Pettitt法突变识别Fig. 9 Runoff M-K and Pettitt method mutation identification under RCP8.5 mode in Nomin River Basin

对于RCP2.6模式,正反向序列曲线存在多个交点,且所处的区间位于上下置信区间内,但从年径流的趋势变化来看,序列的正向曲线均未能够突破上下置信度线。结合Pettitt检验曲线看,该曲线并不存在明显的最低点。因此可认为在RCP2.6模式下诺敏河流域年径流在未来不会突变。

对于RCP4.5模式,正反向序列曲线也存在多个交点,且所处的区间位于上下置信区间内,年径流序列的正向曲线突破了上置信度线,但并不显著。结合Pettitt检验曲线,该曲线存在一个明显的最低点。因此可认为在RCP4.5模式下诺敏河流域年径流在未来存在很大的可能形成突变。

对于RCP8.5模式,正反向序列曲线存在1个交点,且交点位于上下置信区间内,年径流序列的正向曲线明显地突破了置信度线,交点位于2067年附近。结合Pettitt检验曲线看,该曲线存在一个明显的最低点,对应的时间为2067年。因此可认为在RCP8.5模式下诺敏河流域年径流将在2067年附近发生突变,突变后的径流表现为显著的增加。径流的突变特征与趋势特征也表现出了较好的一致性。

4.3.3 径流周期特征分析 对3种模式下2021—2100年的径流进行小波计算,并绘制小波图(图10—12)。对于RCP2.6模式,序列存在3个峰值,对应7,19,56 a时间尺度。其中56 a时间尺度为峰值的最高点,可认为是该序列的第一主周期,7 a时间尺度次之,为序列的第二周期,19 a则对应第三周期。结合实部等值线图可知,虽然30,45 a的时间尺度在方差图上没有明显的峰值特征,但也存在一些周期特征。

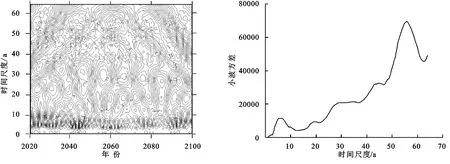
图10 诺敏河流域RCP2.6模式下径流小波系数实部等值线图、小波方差Fig. 10 Real part contour map and wavelet variance map of runoff wavelet coefficients under RCP2.6 mode in Nomin River Basin

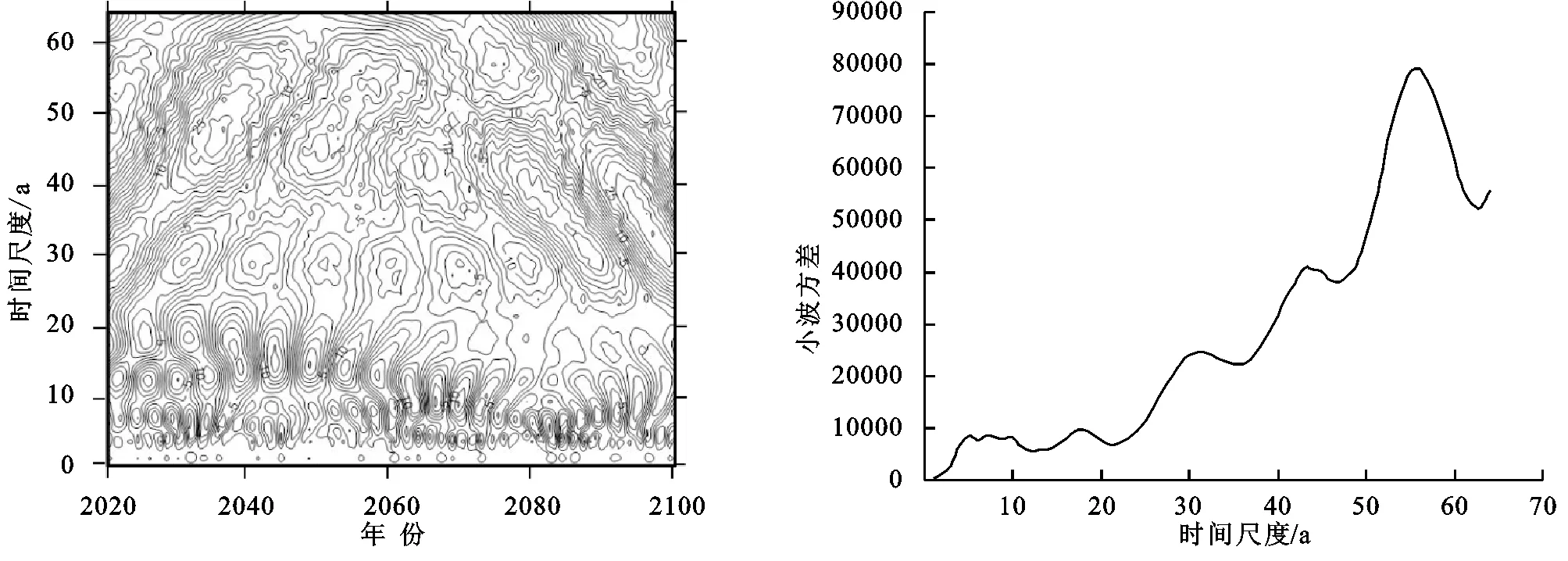
图11 诺敏河流域RCP4.5模式下径流小波系数实部等值线图、小波方差Fig. 11 Real part contour map and wavelet variance map of runoff wavelet coefficients under RCP4.5 mode in Nomin River Basin

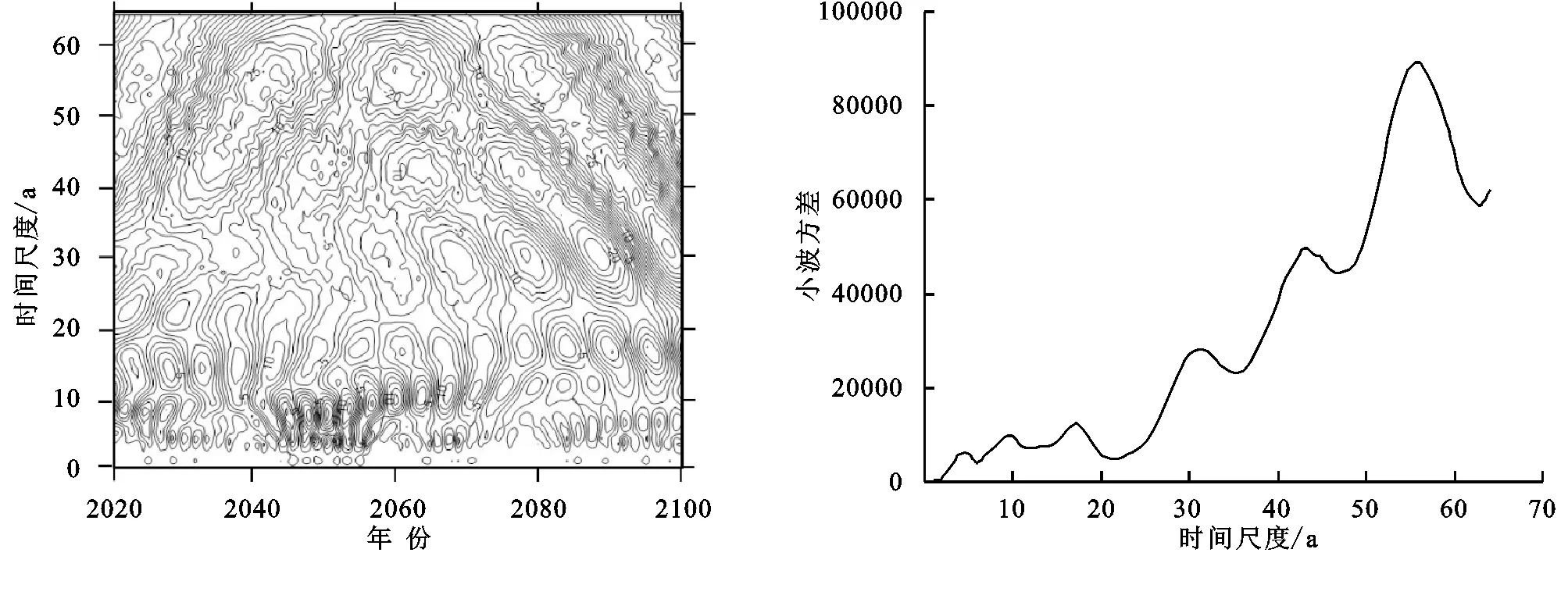
图12 诺敏河流域RCP8.5模式下径流小波系数实部等值线图、小波方差Fig. 12 Real part contour map and wavelet variance map of runoff wavelet coefficients under RCP8.5 mode in Nomin River Basin

对于RCP4.5模式,序列存在4个峰值,对应19,32,44,56 a时间尺度。其中56 a时间尺度为峰值的最高点,可认为是该序列的第一主周期,44 a时间尺度次之,为序列的第二周期,32 a和19 a则对应了第三、第四周期。相比于RCP2.6模式,7 a时间尺度在周期特征变现上产生了波动,而30 a和45 a附近的周期特征得到了更明显的凸显。

对于RCP8.5模式,其周期特征和RCP4.5模式相似,峰值对应的时间分别为19,32,44,56 a。其中56 a时间尺度为峰值的最高点,可认为是该序列的第一主周期,44 a时间尺度次之,对应为序列的第二周期,32 a和19 a则对应了第三、第四周期。

5 讨论与结论

本文用未来气候数据驱动SWAT模型进行气候变化条件下径流特征分析。从趋势上看:3种情景模式下径流都保持增长趋势。其中,RCP8.5模式下增幅最大,21世纪中期保持1.15亿m3/10 a的增速,后期以1.72亿m3/10 a增长。RCP4.5模式其次,在21世纪中、后期分别以0.49亿m3/10 a,0.96亿m3/10 a的增速增长。RCP2.6模式下径流量增长相对较少,在21世纪中期和后期增速仅为每10年0.06亿m3,0.27亿m3。

从突变上看:RCP2.6模式下,诺敏河流域年径流依旧不会突变;RCP4.5模式下,年径流在未来存在很大的可能形成突变。而RCP8.5模式下,年径流将在2067年附近发生突变,突变后的径流表现为显著的增加。

从周期上看:RCP2.6模式下,年径流变化周期主要由56 a时间尺度的主周期控制,7 a和19 a时间尺度对应的次周期控制效果一般;RCP4.5模式下,年径流变化周期主要由56 a和44 a的第一、第二主周期控制,32 a和19 a对应的次周期控制效果不强。RCP8.5模式下,其周期特征和RCP4.5模式相似,相比之下,56 a时间尺度下能量密度更为密集,该周期的控制效果得到进一步增强,而其余几个周期下的控制效果则进一步减弱。

本文在研究的过程中,水文模型、气候模式、降尺度模型中都存在不确定性,怎样量化这些模型在计算中的不确定性,了解计算过程中相互之间存在的分歧,需要更为深入地研究。同时,除气候变化环境因素外,人类活动如砍伐森林、城市化发展等,都会对径流产生较大的影响[25-27],如何定量地区分其中气象要素和人类活动的贡献率也有待进一步分析。