内支撑支护结构风险评估方法及拆撑可行性研究

尹爱月 卢 卓 王旭博 魏焕卫 王介鲲 郑 晓

（1.山东电力工程咨询院有限公司，山东济南 250013；2.山东建筑大学土木工程学院，山东济南 250101）

0 引言

内支撑支护结构因具备支撑力强、适应性强、布置灵活等优势在深基坑项目建设中得到了普遍应用[1]，但依然存在一些不确定因素影响着整个支护结构的安全性，无论是在设计、施工还是使用阶段，稍有不慎将会导致严重的工程事故。据统计显示[2-3]，采用内支撑支护结构形式的工程建设项目中，由于施工过程中操作不当引发的基坑倒塌事故频发，其中，2008年，发生在杭州市萧山区湘湖站的事故[4]是施工不当导致支撑失效从而引发基坑坍塌的典型案例。

越来越多的学者认识到风险分析在基坑工程领域的重要性，并开展了相关的研究。Choi 等[5]研究了基坑工程风险评估的理论及其管理模式，提出了利用模糊不确定模型、风险信息监测表等工具进行风险评估和管理的办法。Gupta 等[6]通过采用熵权双基点法对风险进行优先级排序，并就整体项目延迟来量化风险。黄宏伟等[7]从风险概念上出发，通过对基坑事故的广泛调查，得到了深基坑安全性的主要影响因素及其所占权重，并以此为根据对深基坑安全风险等级进行了评判。陈绍清等[8]提出了事故树与层次分析相结合的风险评价方法，并通过定性地风险识别与定量地风险分析对某基坑工程塌坍事故的致灾因素进行了重要程度排序。张胜昔等[9]利用模糊层次分析法与灰色系统理论，建立了模糊和灰色不确定性评价模型。李鹏飞等[10]基于结构承载能力的冗余度理论，针对排桩内支撑支护的受力特性，提出了新的风险评价方法及对应的风险等级。上述研究成果表明了基坑的风险分析正处于一个由定性向定量发展的过渡阶段，目前，基坑的风险分析仍然以半定量半定性的理论居多，且针对内支撑支护结构的风险分析理论相对较少。

从工程实际的需求出发，将内支撑支护结构典型的变形和内力监测数据归纳为安全评价指标，以监测报警值为评价尺度对各指标进行量化，根据层次分析理论建立了一种基于现场实测数据的风险分析方法，并依托实际工程验证了风险评估方法的合理性，最后利用PLAXIS3D 软件建立有限元三维仿真模型，分析了支撑拆除方案的可行性。

1 内支撑支护结构的风险评估方法

1.1 安全评价指标的确立

在内支撑支护结构的施工阶段，常见的险情主要有：超挖[11]、地下水处理失败、坡顶超载、基坑整体失稳等。如图1 所示，不同风险源所引发的基坑破坏机理不同[12]，其对应的监测指标也随之存在不同的数据响应，如桩顶变形、桩身倾斜、坑底隆起等监测数据均将发生不同程度的变化。同时，监测数据的异常变化可能是基坑事故发生的预兆，监测数据之间存在不同的敏感性及指向性，可将监测指标作为评价支护结构安全状态及风险的依据。

常见的内支撑支护结构主要包括支撑+支护桩、支撑+地下连续墙等形式。通过对实际工程中监测方案[13-14]的调查，选取较为典型的监测指标作为基坑整体安全性风险分析的评价指标，初步确立典型的评价指标主要有：围护墙（桩）测斜、立柱沉降、地表沉降、围护墙（桩）弯矩、支撑轴力、坡顶水平位移、坡顶竖向位移、地下水水位。

1.2 安全评价指标的量化

在施工过程中，现场监测人员通常采用设置监测报警值的方式对基坑进行安全控制，因此，为确保各监测指标均能够在同一评价尺度上反映基坑的安全状态，提出利用各监测指标的报警值对各评价指标进行量化，见式（1）。

式中：si为第i个监测指标对应的安全状态估值；Ua为监测指标对应的实测值；Uw为监测指标对应的报警值。

按式（1）可求解出不同监测指标对应的安全状态估值，但不同安全状态估值之间存在差异性，如果仅通过单一指标的安全状态估值来判断整个支护体系的安全状态和风险是不科学的，故提出通过引入权重系数来建立单一各评价指标之间的联系，见式（2）。

式中：sR为综合考虑不同监测指标影响的整体安全状态估值；ωi为第i个安全状态估值对应的权重。

为求解各评价指标对应的权重系数，采用层次分析法[15]对各监测指标进行重要程度划分，进而得出权重组合系数，层次分析模型可见图2。

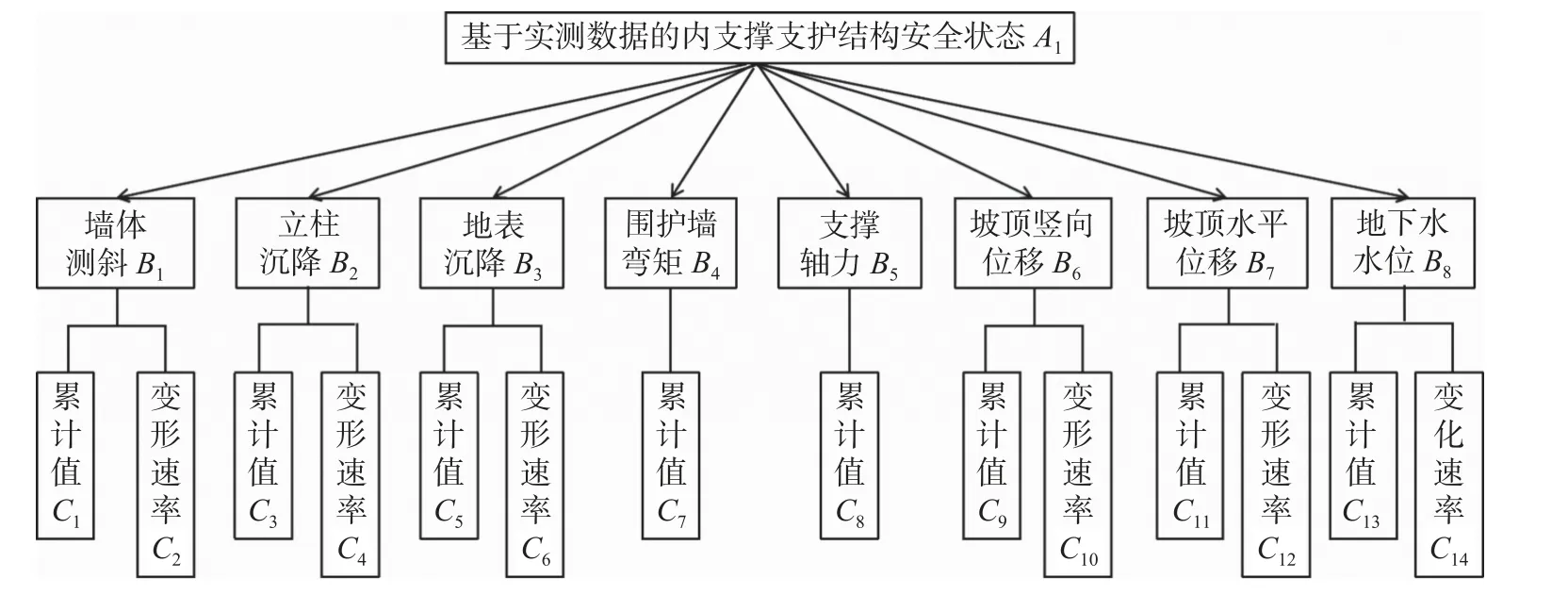
图2 基于现场实测数据的层次分析模型

基于现场实测数据的层次分析模型中，结构层次可分为三层。

目标层事件：A1={B1,B2,B3,B4,B5,B6,B7,B8}；

中间层事件：B1={C1,C2}；B2={C3,C4}；B3={C5,C6}；B4={C7}；B5={C8}；B6={C9,C10}；B7={C11,C12}；B8={C13,C14}；

底层事件：{Ci}；其中i表示具体的监测项目的个数。

建立层次分析模型后，可根据各元素的重要程度构造判断矩阵，见式（3），进而求解各子事件对于上一层事件的权重，为了简化计算，对于底层事件{Ci}的权重按ω=(累计值,变形速率)=[0.7,0.3]或者完全按照二者中的最不利情况赋值，只需对中间层事件{Bi}构建判断矩阵即可。此外，需注意中间层事件{Bi}的数量最好不超过9个，否则过多的子事件元素会影响体系中各个事件之间的重要性判断。

式中：aij根据i、j两个因素相对重要性程度的判断取值，取值可参考表1。

由于判断矩阵为对称分布，aij与aji互为倒数关系，当aij确定时，aji自然也可以确定。当判断矩阵列出后，各评价指标权重系数可通过求解特征向量、求解最大特征值、进行一致性检验等步骤实现，具体过程不再赘述。

1.3 风险度的转化过程

对于传统的风险度主要通过式（4）计算得到：

式中：r为风险度，可视为风险量化的结果；P为风险事件发生的概率；C为风险发生的损失程度。

在深基坑风险分析领域中，P、C的取值往往根据专家调查及打分得出，风险度r值不可避免地存在了较大的主观性。在1.2 节的论述中提出了sR的概念及对应的计算方法，但sR并不代表基坑的实际风险状态，需要进一步转化，故结合监测报警值的概念提出如下的理想假定：

（1）假定实测数据越接近监测报警值时（sR越接近1 时），风险发生的概率P越大，且二者之间存在必然的等价线性关系；

（2）假定监测报警值与极限状态值之间存在的安全储备可以用结构重要性系数γa、支护结构综合分项系数γF、极限值与设计值之比γy的乘积β表达。则有：

（3）假定各安全评价指标的风险损失程度C可以用各监测指标对应安全状态估值si的归一化进行代替，则有：

联立式（4）-式（6）可得风险度r为：

式中：r为基于现场实测数据推导得出的风险度；β为安全储备系数；为了避免极端条件的存在，当时，对应公式中分母项应取值为1 进行计算。

r为不大于1 的无量纲评价值，其大小直接反映此时内支撑支护结构的风险程度，按照多级预警原则将风险度进行等级划分并建立相应的决策准则，见表2。

2 风险评估的工程实例分析

2.1 工程概况

拟建的工程项目为一大型翻车机房及配套地下运转站，如图3 所示，基坑整体形状不规则，呈“凹”字形分布，东西长度约130 m，南北长度约50 m，基坑各区的开挖深度不尽相同，基坑北侧（区域二、区域三）、南侧（区域一）、东侧（区域四）对应的开挖深度分别为22 m、14.5 m、14.3 m。

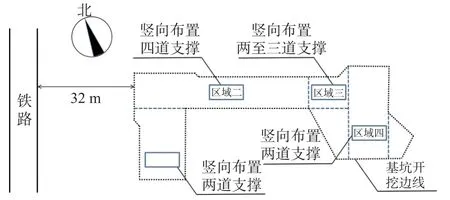
图3 基坑平面布置图

基坑采用支护桩+钢筋混凝土内支撑的支护形式，基坑南北走向设置2 道支撑，东西走向设置4 道支撑。以开挖深度最深的区域二为例，基坑深度约为22 m，支护桩采用直径为1000 mm 的混凝土灌注桩，嵌固深度为16.1 m，沿基坑深度方向共布置4 道混凝土对撑（截面尺寸：1000 mm×800 mm），支撑的水平间距约为5 m（见图4）。

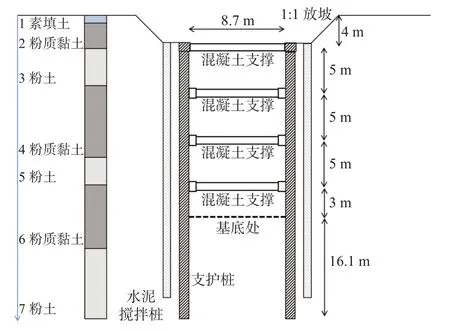
图4 基坑北侧支护剖面图

拟建场地的主要地层为第四系黄河三角洲的沉积土层，地下水类型属于孔隙潜水，地下水的稳定水位埋深为3.0 m。根据钻探揭露，结合相应的土工试验，开挖范围内的土体自上而下可划分为7层，各土层的物理力学指标见表3。

2.2 施工工况

基坑施工过程中的主要分项工程为：（1）进行支护桩和止水帷幕的施工；（2）采用降水井进行坑内降水；（3）分区段、分步开挖的同时依次浇筑架设混凝土支撑直至开挖至基底。由于基坑北侧（区域二）的开挖深度最深，为此主要对该支护区段进行分析，其具体开挖及设撑的施工工况见表4。

表4 区域二开挖及设撑施工工况统计

2.3 基坑监测区域分割及监测指标

如图5 所示，该基坑工程的主要监测项目有桩体测斜、支撑轴力、桩顶冠梁位移、地表沉降、立柱沉降、地下水水位等。在进行风险评估前，为避免基坑空间效应对不同位置测点的影响，按照就近原则将基坑分割成7 个不同的分析区域，且分析区域内的监测指标即为该区域的安全评价指标。

图5 基坑测点的分布及区域划分示意图

各分析区域内的评价指标确定后，根据相应的监测规范[16]以及工程实际状况，确定图5 中各评价指标的监测报警值（见表5）。

表5 监测指标报警值统计

2.4 风险度变化分析及风险源识别

由于桩体测斜的测点布置广泛、数据结果可靠，同时，综合各类险情引发的事故来看，桩体测斜在面对基坑风险的发生时，始终保持着较高的数据敏感性，因此在建立判断矩阵时，赋予其较高的分值，最终求解的各分析区域的权重系数如下：

分析区域①：(桩体测斜∶支护桩弯矩∶支撑轴力∶立柱沉降∶地表沉降∶坡顶沉降∶坡顶水平位移)=[0.37∶0.25∶0.12∶0.12∶0.06∶0.05∶0.03]；

分析区域②：(桩体测斜∶支护桩弯矩∶支撑轴力∶立柱沉降∶坡顶沉降∶坡顶水平位移)=[0.39∶0.25∶0.14∶0.12∶0.06∶0.04]；

分析区域③：(桩体测斜∶支护桩弯矩∶地下水位∶坡顶沉降∶坡顶水平位移)=[0.42∶0.30∶0.12∶0.1: 0.06]；

分析区域④：(桩体测斜∶支护桩弯矩∶支撑轴力∶地下水位∶坡顶沉降∶坡顶水平位移)=[0.39∶0.25∶0.14∶0.12∶0.06∶0.04]；

分析区域⑤：(桩体测斜∶支护桩弯矩∶支撑轴力∶坡顶沉降∶坡顶水平位移)=[0.42∶0.30∶0.12∶0.1∶0.06]；

分析区域⑥：(支护桩弯矩∶桩体测斜∶支撑轴力∶坡顶沉降∶坡顶水平位移)=[0.42∶0.30∶0.12∶0.1∶0.06]；

分析区域⑦：(桩体测斜∶支护桩弯矩∶支撑轴力∶坡顶沉降∶坡顶水平位移)=[0.42∶0.30∶0.12∶0.1∶0.06]。

按照上述权重组合系数，结合式（1）、式（2）、式（7）对5 月7 日至8 月14 日100 d 内监测数据的风险度进行计算，计算结果如图6 所示。

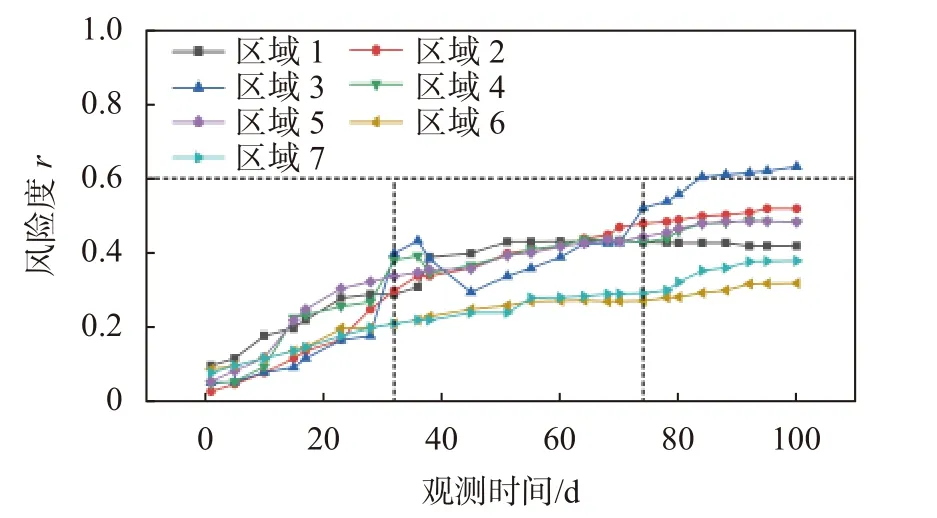
图6 基坑分析区域风险度的时程曲线

对于基坑南侧开挖深度较浅的区域①、⑥、⑦的最终风险度基本维持在0.4 左右，此时对应的风险等级分别为三级、二级、二级，其中，区域①风险度较大的原因可能是施工过程中开挖速度过快；对于基坑北侧开挖深度较深的区域②、③、④、⑤的最终风险度均在0.4 以上，对应的风险等级分别为三级、四级、三级、三级，其中，区域③的最终风险度最大，主要是该区域附近止水帷幕破坏造成基坑漏水所致。为此，查看了该区域内监测数据的变化情况，如图7、图8所示，该区域内CG1 水位监测点于观测的第30 d、74 d 发生了两次水位骤降，且超出了报警值规定的2 m/d，同时邻近支护桩CX3 测斜点的最大水平位移也在该时间段内产生了两次较大的突变，通过与实际的工程记录比较发现，在观测的第30 d（即6 月4 日）基坑发生了较为严重的漏水，这说明根据风险度的变化情况察看监测数据具备一定的风险识别功能。

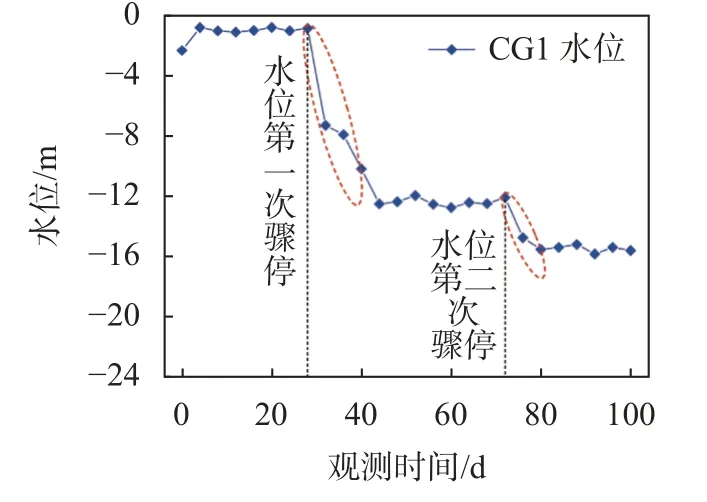
图7 CG1 测点地下水水位变化情况

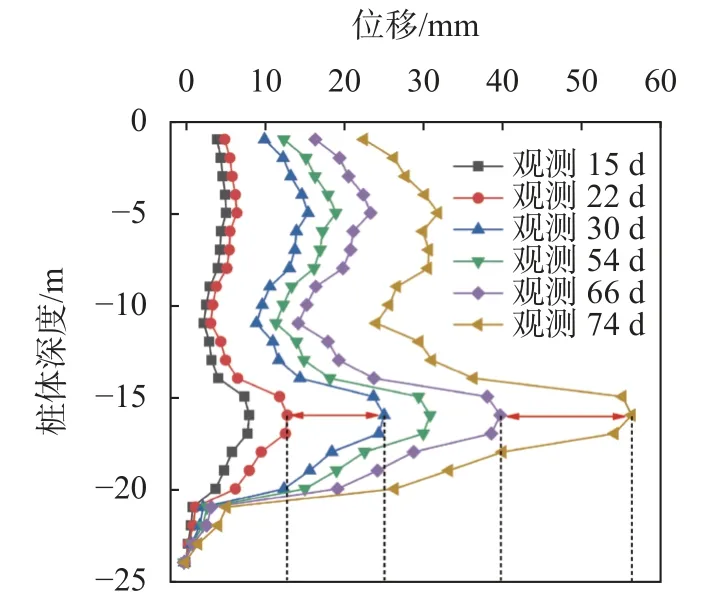
图8 CX3 测点桩体测斜变化情况

根据最终风险度的变化情况，对照表2 确定的风险决策方案应为：

（1）立即停止区域③及其邻近区域的下一步施工作业，对漏水位置进行排查堵漏，确保隐患消除后才可继续施工，时刻保持高度警惕，加强对监测数据的密切关注，应注意风险度0.8 及以上是基坑安全状态的红线，如果后续风险度值达到0.8，说明基坑存在重大风险隐患，应立即停止基坑全部区域的施工；

（2）加强对基坑风险等级为三级区域的日常监控，应把风险度值严格控制在0.6 以内，如若后续风险度超过0.6 应立即排查该区域内可能存在风险隐患并采取必要控制措施；

（3）对于基坑风险等级为二级的区域，继续保持当前的监测和各项施工管理安排，日常中注意观察该区域后续的风险度变化速率即可。

3 支撑拆除方案的可行性分析

由于工程后期涉及到拆除支撑的环节，为讨论支撑拆除方案的可行性，建立PLAXIS3D 有限元仿真模型，利用数值计算结果结合风险评估方法对基坑拆撑阶段的风险度变化情况进行分析。

3.1 有限元模型的建立

如图9 所示，模型尺寸及工况设置按照实际工程进行模拟，支撑、腰梁、立柱构件采用梁单元模拟，支护桩则采用板桩墙单元模拟，并在单元底部约束其X、Y、Z三个方向的位移，在桩体等效为板的过程中，可按照将桩体直径通过式（8）转化成墙体厚度。

式中：D为灌注桩直径，mm；t为桩间距离，mm；h为折算板的厚度，mm。

土体本构模型采用HS（土体硬化）模型[17]，各土层参数的选取见表6，模型支护构件参数见表7。

表6 模型中的土体参数设置

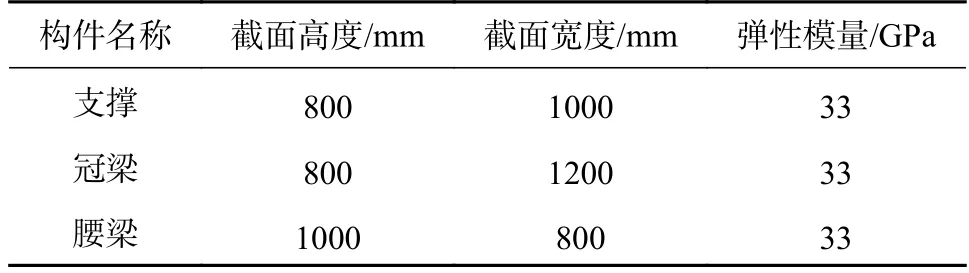
表7 模型中的支护构件参数设置

关于模型中的施工步设置主要参考了实际工程的施工工况（见表4）。

3.2 模型计算结果验证

为验证模型计算结果的合理性，取图6 中CX4测点位置在开挖至基底的实测数据进行对比，如图10所示。水平位移实测值和模拟值在整体变化趋势上基本一致，曲线呈现“中间大、两头小”的形态，模拟计算得出的侧向变形最大值分别为35.1 mm，与对应的实测值相差6.2 mm，存在一定误差的主要原因是实际工程中受到施工等因素的干扰，这些情况在模拟计算中无法考虑到。总体而言，数值模型的计算值偏小，但变化趋势与实际情况吻合较好，可以用于预判研究。

图10 CX4 桩体测斜的实测值与模拟值对比

3.3 支撑拆除阶段的数值模拟及结果分析

选取图4 中基坑开挖深度最深的区域二作为拆撑阶段可行性分析的研究对象，该区域具体的支撑拆除方案为：（1）在基坑开挖至基底后，对基坑底板进行浇筑；（2）对下层的主体结构墙体及顶板进行施工；（3）等待养护强度达标后，土体回填至拆撑位置处；（4）依次对支撑进行拆除，并重复上述（2）-（4）步骤。为模拟支撑的拆除阶段，同时又考虑到模型计算的可操作性，在3.1 节原有数值模型的基础上建立新的工况，通过改变模型中板桩墙单元材料属性的方式模拟主体结构墙的施加，同时以施加整体板单元的方式模拟主体结构板的施工，具体工况的模拟如图11 所示，其中，结构墙单元与板单元的连接方式为固接，新增的结构墙单元设置的厚度为1 m、弹性模量为30 MPa，结构板单元设置的厚度为0.8 m、弹性模量为30 MPa，其余的土体参数与表6 中相同，模型支撑拆除的具体操作为沿y轴方向顺次进行材料的冻结。

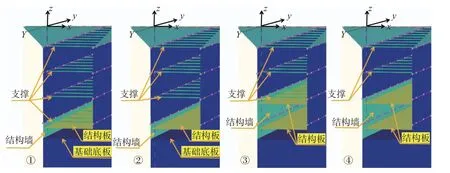
图11 基坑北侧（区域二）支撑拆除的模型剖面图

提取模型中对应CX4 测点剖面处的桩体测斜及弯矩，分析其在拆撑后的变化情况。如图12 所示，当拆除下层支撑后，围护桩上部的水平位移增长了近2 mm，主要是由于拆撑过程中原本支撑所受的轴力释放并传递至主体结构墙及结构板，但桩体深层水平位移的最大值在支撑拆除过程中未发生明显增长，可见结构墙与结构板有效地承担了原本支撑所释放的荷载。如图13 所示，桩体弯矩在支撑拆除过程中明显减小，最大弯矩由792 kN·m 减小为425 kN·m，减小了46.3%，结合桩体的水平位移变化情况可知，弯矩的减小主要由于桩体上部向坑内位移产生卸荷效应以及主体结构墙及结构板承担了原有荷载。

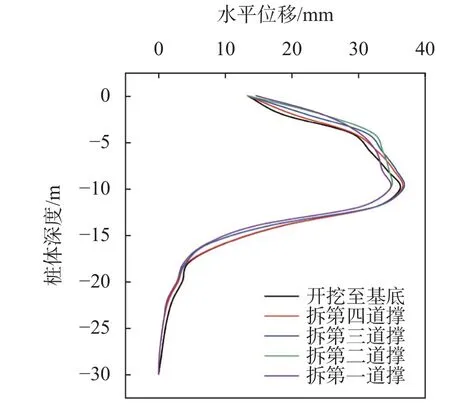
图12 CX4 测点拆撑阶段的桩体测斜变化情况

3.4 支撑拆除阶段的风险度变化分析

提取CX4 测点剖面位置的桩体测斜、桩体弯矩、坡顶水平位移、坡顶沉降、支撑轴力作为拆撑可行性分析的评价指标，进行风险度计算。如图14 所示，按照3.3 节中的拆撑方案进行，基坑风险度始终处于稳定的发展态势，且随着支撑的拆除风险度有所下降，最终由0.43 下降至0.35，说明采取先浇筑主体结构墙、结构板进而再拆除支撑的方案可行，但具体的施工过程中应保持对实测数据的关注。

图14 支撑拆除阶段风险度时程曲线

4 结论

依托某内支撑支护基坑工程，对基于现场实测数据的风险评估理论方法进行了验证，并利用PLAXIS3D 有限元软件建立三维仿真模型，分析了支撑拆除方案可行性，得出的主要结论如下：

（1）经风险评估分析，该工程的基坑整体风险等级为三级、局部区域为四级，风险源主要为地下水渗漏。基于现场实测数据的风险评估理论方法能够有效利用工程的实测数据，其评价方法合理可靠，可动态反映基坑的风险度变化情况，除在权重系数赋予过程中存在一定主观性之外，其余评价过程较为客观。

（2）各评价指标对应权重的取值是影响基坑风险等级的关键；桩体测斜作为主要的安全评价指标，在风险分析过程中应发挥控制作用；建议在实际工程中风险度严格控制在0.6 以下，以确保基坑处于安全状态。

（3）本文提出的风险分析方法不仅能够依托实测数据进行计算，同样可以与数值模拟计算结果相结合，对即将进行的工况作出可行性分析，表明该方法存在较大的应用发展空间。