考虑粒径对砂土宏细观剪切性质的试验研究
王 博 吕 果 李 江
(建设综合勘察研究设计院有限公司,北京 100007)
0 引言
砂土宏观上具有离散性和非均匀性,微观上具有多样性和易变性[1],在路基工程、山区边坡防护等工程领域中较为常见,保证其稳定性尤为重要,因此分析砂土的抗剪能力极为关键。
目前,关于砂土剪切特性研究主要从实际试验和模拟试验两方面开展,对于实际试验而言,Been 等[2]通过采用状态参数来描述Kogyuk 砂的剪胀性。郝冬雪等[3]进行砂土三轴剪切试验,发现高压下砂土应力-应变曲线后期无应变软化现象。对于模拟试验而言,刘方成等[4]在砂土中掺入橡胶,进行了直剪试验离散元模拟,从力链和颗粒位移等分析了细观机制的变化;李 航等[5]从颗粒形状和孔隙率出发,模拟了标准砂剪切;杨忠平等[6]、张振平等[7]利用颗粒离散元软件进行了土石混合体直剪试验模拟,均得出了混合体抗剪强度随含石量增加而增加的结论。
尽管众多学者在砂土剪切特性方面取得了一定研究成果,但所采用砂土均具有单一性,没有考虑砂土粒径对其力学特性的影响。河砂作为一种在工程领域常见的土体,通常粒径变化范围较大,研究其不同粒径下的剪切特性对于砂土稳定性研究尤为关键。为此,利用应变控制式直剪仪进行3 种不同平均粒径砂(分别对应细砂、中砂和粗砂)的直剪试验,分析了剪切应力-剪切位移关系和界面抗剪强度指标等宏观力学变化,建立了砂土抗剪强度预测模型。此外,开展离散元PFC2D 进行砂土直剪试验,对不同平均粒径下的剪切带厚度变化规律进行分析,针对通过改变砂土粒径提升砂土抗剪能力进行研究。
1 试验设备、材料、方案
1.1 试验设备及材料
试验设备为ZJ 型直剪仪(见图1),上下剪切盒通过插销构成整体,试验准备前先放置透水石,再放置砂土,最后放置透水石。砂土试样直径6.18 cm、高度4 cm。试验所用砂土为某工地河砂,将砂土烘干后分为3 个粒组,分别为0.075~0.25 mm(细砂)、0.25~0.5 mm(中砂)和0.5~2 mm(粗砂),如图2 所示。砂土的土粒比重Gs为2.64,三种砂土取平均粒径dⅠ、dⅡ和dⅢ分别为0.15 mm、0.36 mm 和1.22 mm,初始密度ρ分别为1.37 g/cm3、1.40 g/cm3和1.45 g/cm3,剪切试样直径为61.8 mm、高为20 mm。

图1 应变控制式直剪仪示意图

图2 试验用砂
1.2 试验方案
试验剪切速率为0.8 mm/min,考虑因素为3 种不同的平均粒径,4 种法向应力(50 kPa、100 kPa、150 kPa 和200 kPa),共12 组试验。
2 宏观试验结果分析
2.1 剪切应力-剪切位移特征曲线
剪切应力-剪切位移特征曲线见图3,通过对图3 分析发现,剪切应力随剪切位移先快速增大后缓慢增大,到达抗剪强度后基本稳定。汇总出各情况下抗剪强度(见表1),由表1 可见,在同一平均粒径下,法向应力越大,抗剪强度越大,但增大幅度基本一致。在同一法向应力下,砂的抗剪强度随砂土平均粒径的增加而增加。
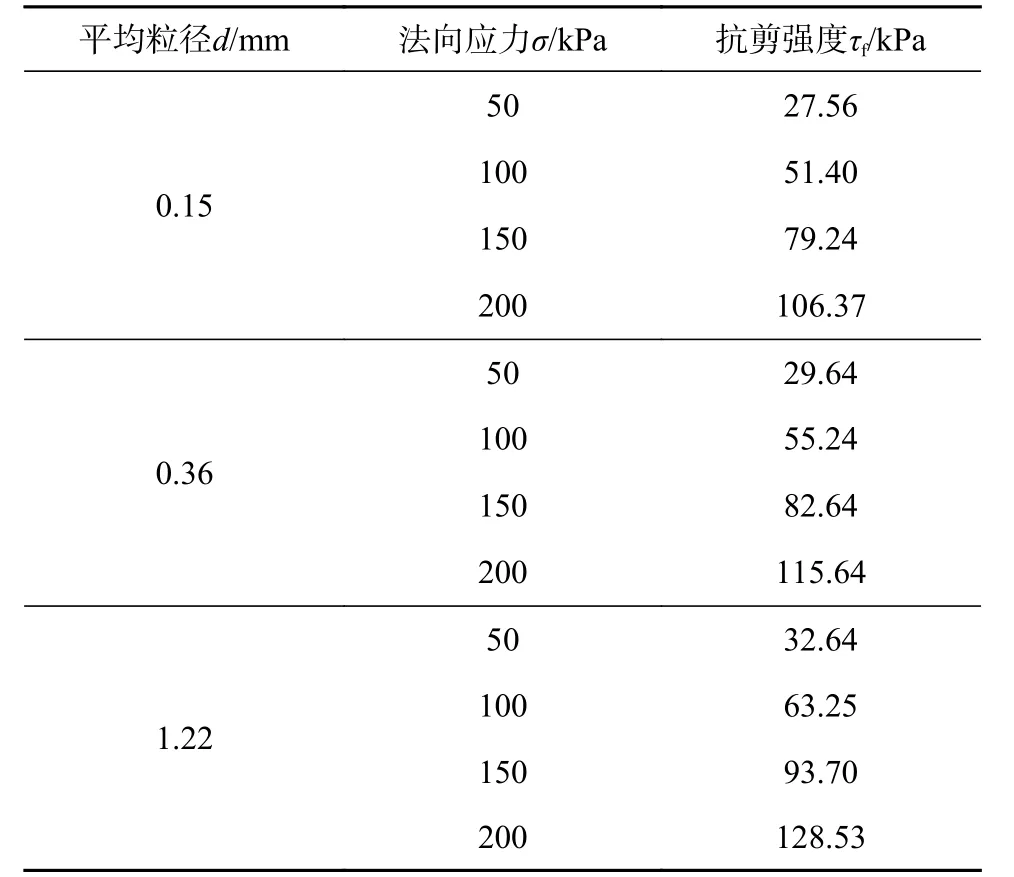
表1 各情况下抗剪强度表

图3 剪切应力-剪切位移特征曲线
2.2 抗剪强度的预测
以法向应力σ和平均粒径d作为自变量,以抗剪强度τf作为因变量,进行多元线性回归分析,可以进行抗剪强度的预测,公式如下:
式中:β0、β1、β2为回归系数。将2.1 节中数据代入式(1),回归后得到多元线性回归关系为:
将试验抗剪强度与预测抗剪强度绘制到图4中,发现预测与试验走势相同,数据基本一致,说明该多元线性模型回归效果良好,利用法向应力σ和平均粒径d来测算抗剪强度τf较为准确,可以应用于实际工程。

图4 模型与试验数据对比
2.3 抗剪强度指标分析
在岩土领域,有多种土体破坏准则,例如:Tresca破坏准则、Drucke-Mises 破坏准则、Mohr-Coulomb 破坏准则和双剪破坏准则等[8]。对于干砂而言,黏聚力c为0,因此适合采用Coulomb 破坏准则对抗剪强度τf与法向应力σ间的关系进行表达,具体表达式如下:
式中:φ为内摩擦角。
图5 为抗剪强度-法向应力关系,可以看出:相关系数R2均在0.999 以上,Coulomb 破坏准则表达准确。同样发现抗剪强度随法向应力和平均粒径的增加而增大。通过式(1)得出平均粒径dⅠ、dⅡ和dⅢ对应的内摩擦角分别为27.88°、29.55°和32.46°,可见内摩擦角随平均粒径的增大而增大。

图5 抗剪强度-法向应力关系
3 剪切带厚度规律分析
砂土在剪切结束后产生剪切带,剪切带厚度是岩土界关注的重点,而常规的室内试验无法观测到剪切带,也无法确定其厚度,只能借助离散元等微观软件进行判断。离散元法作为描述颗粒土力学特性的数值分析手段被广泛应用于岩土工程领域[9-10],常用的离散元模拟软件为PFC2D 或3D 模拟软件,本文采用PFC2D 进行不同平均粒径下剪切带厚度分析。
3.1 模型建立及试验方案
3.1.1 模型假设与尺寸建立
模型假设颗粒均为刚性体,且为圆形;颗粒与颗粒间通过点进行连接接触,且受力可以发生平移、转动。设置①-⑥号广义墙,其内部放置土体颗粒,如图6 所示。对于①-③广义墙模拟上剪切盒、④-⑥广义墙模拟下剪切盒,为了与室内常规直剪仪盛放土体的尺寸相同,剪切盒整体尺寸为6.18 cm(长)×4 cm(高)。设定④-⑥固定不动,为了消除惯性力对剪切试验的影响,通过控制应变率使①-③墙向右运动缓慢均匀运动。为与室内试验结合,平均粒径分为dⅠ、dⅡ和dⅢ三种,即为0.15 mm、0.36 mm 和1.22 mm,但采用改颗粒尺寸计算时间长、效率慢,因此采用粒径放大法[11],将平均粒径dⅠ、dⅡ和dⅢ尺寸扩大3倍,即为0.45 mm、1.08 mm 和3.66 mm。

图6 土体直剪试验PFC2D 离散元模型
3.1.2 模型参数设置
本模拟试验中接触问题均采用线性刚度模型,公式为:
式中:kn、ks分别为法向、切向接触刚度,k[A]、k[B]表示任意两个接触实体单元的颗粒刚度,对于颗粒间和颗粒-墙体间的法向接触刚度,取值分别为1×108N/m和4×108N/m,同样的,切向接触刚度取值分别为1×108N/m 和4×108N/m。
3.1.3 模拟方案
为与室内试验对比,平均粒径分为dⅠ、dⅡ和dⅢ三种,法向应力分50 kPa、100 kPa、150 kPa 和200 kPa 四种,剪切至位移4 mm 结束试验,剪切速率基本与室内试验一致。由于室内宏观试验与模拟试验土体摩擦系数有较大差别,因此结合室内摩擦系数进行参数调整,即为调参过程。最终确定3 种平均粒径下的土体摩擦系数分别为0.22、0.25 和0.30。
3.2 细观结果分析
3.2.1 模型合理性验证
由于篇幅有限,因此仅展示部分试验与模型的剪切应力-剪切位移关系(见图7)。通过对图7 分析发现,通过PFC2D 模拟得出的数据与试验数据差距不大,两者曲线走势基本一致,这充分说明模型建立合理,可以用于剪切带微观分析。
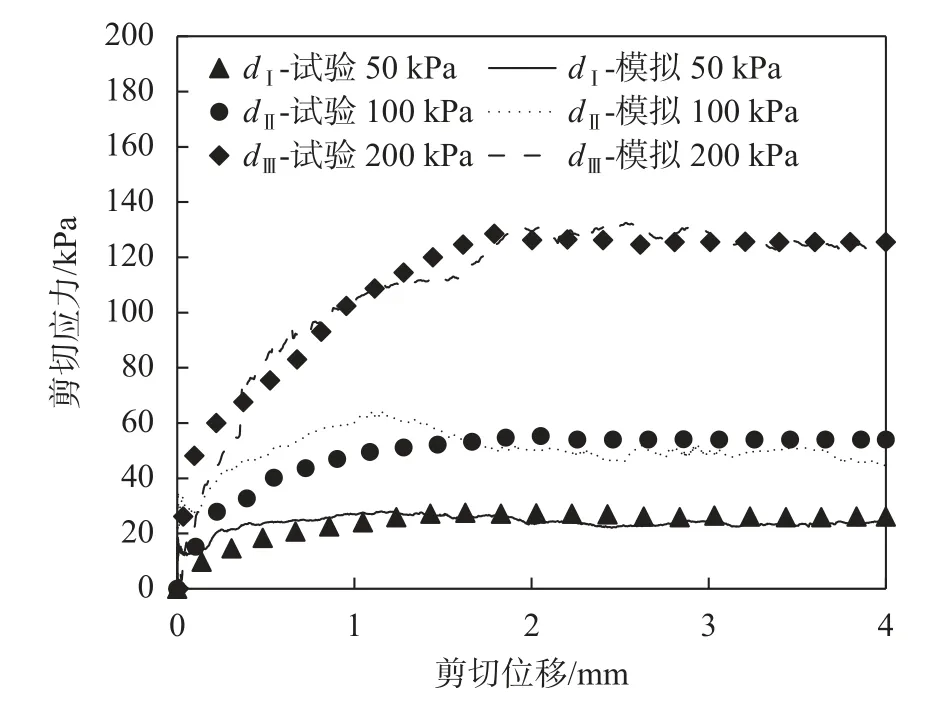
图7 剪切应力-剪切位移试验与模型对比
3.2.2 不同平均粒径下剪切带规律分析
剪切后期,剪切应力处于稳定状态,此时可进行剪切带厚度的确定。为了便于剪切带厚度分析,因此对颗粒进行染色处理,处理为10 条绿色和10 条红色,以平均粒径Ⅰ进行说明,见图8(a),剪切试验初始状态,10 条绿色和10 条红色均为垂直分布,当剪切完毕后,在剪切界面处颗粒发生错动,以错动的垂直距离定义为剪切带厚度L(见图8(b))。

图8 剪切带厚度观条设置示意图
图9 为不同平均粒径下剪切带厚度变化,发现砂土平均粒径越大,剪切带厚度越大,其中平均粒径dⅠ到dⅡ的增加幅度小于dⅡ到dⅢ。法向应力越大,剪切带厚度同样越大,但增加幅度越来越小。此外,发现剪切带厚度L与法向应力σ存在一元二次函数关系:

图9 不同平均粒径下剪切带厚度变化
式中:a、b和c为拟合参数,汇总函数见表2,发现相关系数R2均在0.99 以上,拟合关系良好。
4 结论
利用应变控制式直剪仪,进行了3 种不同平均粒径砂的室内直剪试验和离散元模拟试验,得出以下结论:
(1)砂的抗剪强度随砂土平均粒径的增加而增加。以法向应力σ和平均粒径d为自变量,建立了砂土抗剪强度τf多元线性预测模型,且模型预测准确,对工程有一定实际意义。此外,内摩擦角随平均粒径的增大而增大。
(2)剪切带厚度随平均粒径的增大而增加,其中平均粒径dⅠ到dⅡ的增加幅度小于dⅡ到dⅢ。剪切带厚度与法向应力之间符合一元二次函数关系。
综上两点结论,在实际工程施工中,合理采用粒径较大的砂土有利于提高抗剪能力,增加工程稳定性。

