基于压缩曲线的非线性弹性地基上结构内力与沉降分析

高兴和 张 峰 吕 犇 李 灿

（1.江苏省太湖水利规划设计研究院有限公司，江苏苏州 215100；2.河海大学力学与材料学院，江苏南京 210000）

0 引言

地基沉降，尤其是过大的不均匀沉降会给建筑物带来较大的危害[1]，如上部结构开裂、建筑物倾斜、倒塌等。因此，在水利、市政、道桥等工程设计时，必须根据建筑物等级、地质状况对地基的沉降变形进行验算，并视验算结果采取相应的工程措施来保证建筑物在后期管理运行过程中不发生过大的沉降和沉降差。

弹性地基上的梁板计算是水利工程中重要的问题，水工建筑物必须建筑在地基上，因此结构物的设计离不开对基础梁板的设计。然而基础梁板的计算是非常复杂的问题[2]，主要体现在弹性地基的变形，尤其是不均匀沉降对上部结构的影响。

针对地基土体的应力变形计算，各国学者提出了较多土体本构模型，从最初的线弹性模型到非线性弹性的邓肯-张非线性模型与剑桥模型，再到莫尔-库仑等弹塑性模型[3-6]。计算经验显示，若直接采用线弹性模型，则无法考虑土体变形的非线性，计算结果偏差较大。而精细的本构模型往往因工程试验条件和成本的原因，在使用上受到了限制。

压缩曲线（e-p曲线或e-lgp曲线）是土工试验最直接的成果，因其积累了大量的实践经验，并且本身就能直观地体现土体的非线性，具有足够的精度，国内现行规范[7-9]基本上推荐基于压缩曲线的分层总和法作为沉降计算的基本方法。孙明正等[10]基于土体的e-p曲线，给出计算邓肯-张模型参数的简单方法，并用于弹性地基的计算，取得了较好的结果。蒋忠信[11]针对深圳市地基沉降计算中因压缩参数取值而造成沉降结果差值较大的问题进行了讨论。

本文从弹性理论进行推导，通过压缩曲线获取土体在不同应力条件下的切线模量，采用有限元进行地基土体的数值计算，较为方便和准确地获得土体的应力变形。该方法既可以快速简便地求解土体沉降，又可以通过地基-结构整体计算，获得弹性地基上结构的应力变形，有一定的应用价值。

1 压缩曲线和切线弹模

1.1 e-p 曲线与分层总和法

土的压缩性指标通常由室内侧限固结试验获得。通过该试验可获取各级压力与其对应的稳定孔隙比之间的关系，即e-p曲线或e-lgp曲线。压缩曲线反映了土体的孔隙比和所受压力的关系，直观体现了土体的压缩性质和变形的非线性。

对于分层总和法[12-13]，当前各设计规范规定略有差别，但总体计算步骤类似：

（1）计算压缩层的自重应力和附加应力，自重应力可直接由公式得到，附加应力采用查表或者布辛内斯克（Boussinesq）解得到竖向附加应力分布；

（2）获取压缩层的孔隙比e，由每个压缩层的附加应力及自重应力在压缩曲线上得到对应的孔隙比；

由此可以看出，分层总和法属于手算方法，涉及查表、插值、叠加求和，计算较为繁琐，同时只能一次计算一个点的沉降，结果离散且不直观。

1.2 切线弹性模量

根据弹性理论，弹性模量E和压缩模量Es满足式（1）关系：

式中：μ为泊松比，一般为0.2～0.4。

现假设e-p曲线满足式（2）函数关系：

进一步可求得任意压力所对应的切线压缩模量Es，其一般形式满足式（4）：

则切线弹模的一般形式满足式（5）：

由式（5）可知，切线弹模E与泊松比 μ、竖向压力p有关，而泊松比一般变化较小，可以取固定值或者采用相应拟合得到[14]。由此建立的应力变形的非线性关系可体现地基在高应力下的压硬性，且直接由压缩曲线推导获得，因此认为具有相对较高的精度。在分层总和法中，泊松比 μ与计算过程并没有直接的关联，而泊松比实质反映了侧向位移对于沉降的影响，出于简化，分层总和法并没有直接对侧向位移进行考虑，所以分层总和法实际可等效为单向压缩模型，对应的泊松比 μ为零。令 μ=0，此时切线弹模与压缩模量等价。因切线模量计算公式考虑了泊松比，相当于考虑了水平位移的影响，因此将得到比分层总和法更为切合实际的计算结果。

1.3 计算实现

由于切线弹模E与压力p的非线性关系，此时求解为典型的非线性问题。经有限元的离散之后，可转化为求解以下非线性方程组：

式中：刚度矩阵K(δ)与位移向量δ 相关。

采用荷载增量法，在对R分解成若干荷载增量后，非线性方程转换为：

式中：K(δm)由δm确定，为常数矩阵；ΔRm为第m个增量荷载矢量；Δδm为该增量荷载矢量作用所产生的位移增量矢量。

在有限元法计算自重应力场时，初始计算的弹性参数E、μ可取经验值，确定初始的刚度矩阵K0，后续可以根据计算结果更新弹性模量并迭代。计算显示弹性参数对于地基应力影响不大。同时，土体的压缩特性由当前的应力状态和固结应力共同决定，通过前期固结应力判断是否处于超固结状态，从判断选用回弹-再压缩曲线或者原始压缩曲线确定切线弹性模量。

2 算例及分析

2.1 算例一：条基的沉降

（1）算例介绍

某墙下条形基础[15]，如图1 所示，其宽度为2.0 m，上部结构传至基础的荷载为100 kN/m，埋置深度为1.2 m，地下水位在基底以下0.6 m，压缩试验数据见表1。

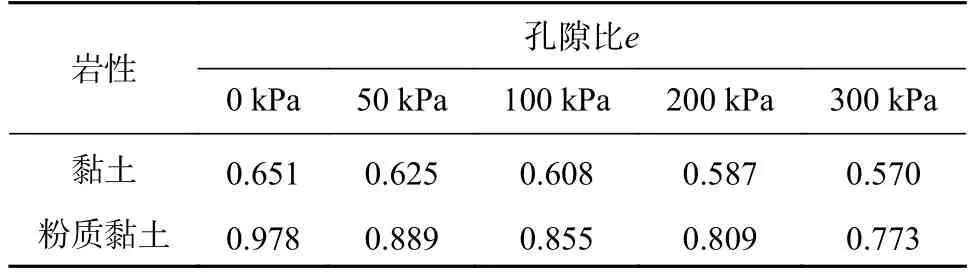
表1 不同压力下的孔隙比

图1 条形基础

（2）计算结果

根据分层总和法规定取地基沉降计算深度为6.4 m，为进行对比分析，对有限元模型取同样厚度进行计算，得到条基中点处的沉降为50.2 mm，整体y方向位移（即竖向的沉降）云图见图2。

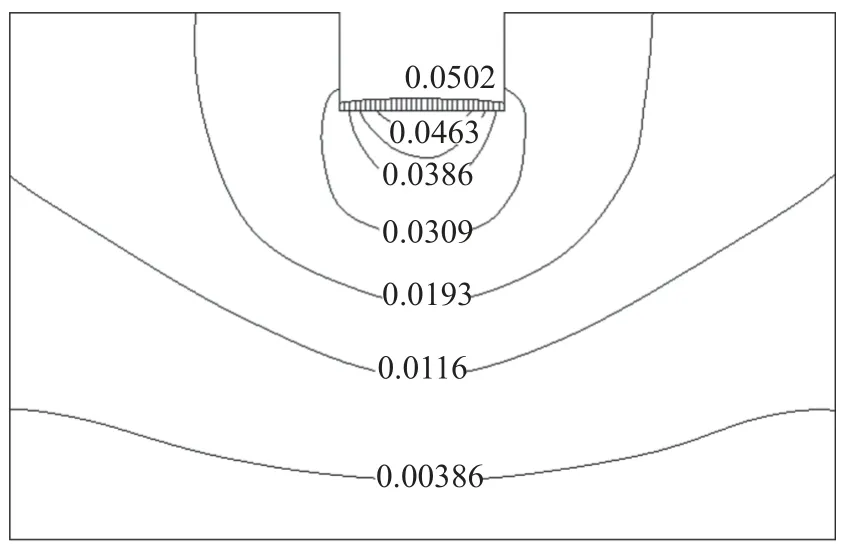
图2 y 方向位移云图（单位：m）

按照分层总和法对条基的沉降进行计算。地基可分为7层，基础中心处的沉降为49.4 mm，略小于本文数值方法的结果，差值为0.8 mm，差值率为1.61%。

（3）结果分析

1）附加应力：对比有限元数值计算中的附加竖向应力与分层总和法查表结果（见表2），可见二者有一定的差别，但数值上差距不大，其原因为解析法结果与有限元数值计算结果的差别。另外，查表中的插值也会出现一定的误差。

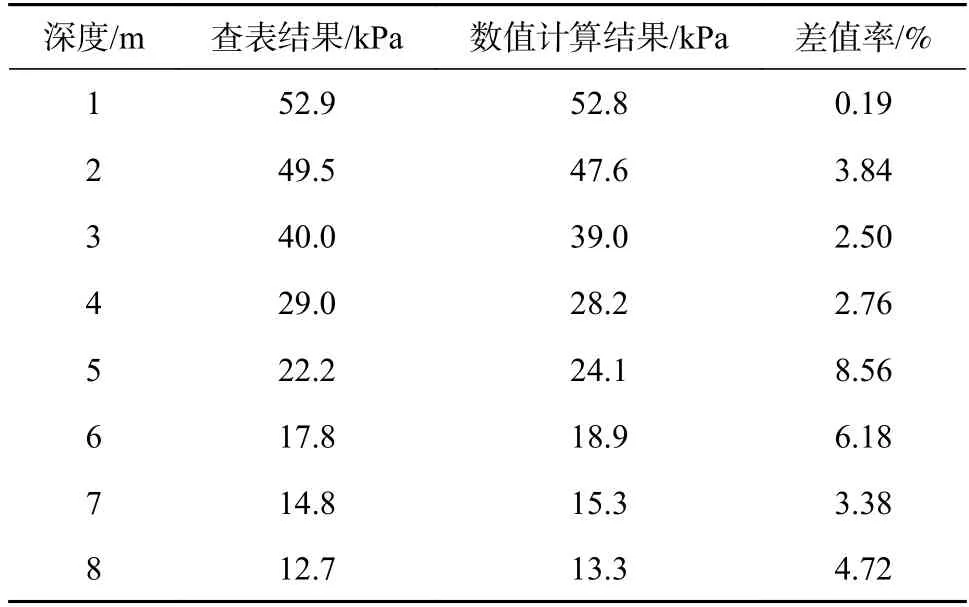
表2 附加应力对比

2）地基厚度：根据有限元计算经验可知，地基厚度对有限元沉降计算影响较大，为此取不同厚度地基对沉降进行计算，结果见表3。

表3 不同地基厚度下的沉降

由结果可见，地基厚度较小时，沉降变化较为迅速，在厚度到6 m 之后，沉降的变化趋势明显减缓，到8～10 m 阶段，沉降基本稳定，表明采用本文方法的沉降计算结果是稳定的。这也可以从e-p曲线上得到解释，在p值达到120 kPa 之后，曲线变得较为平缓，其斜率也变得较小，压缩模量和切线弹模变得较大，因此本文计算方法能较好地体现出土体变形的非线性和压硬性，其结果也较为合理。

3）有限元网格：进一步研究程序的计算精度，调整单元大小，分别取网格尺寸大小0.1 m、0.2 m、0.3 m、0.4 m 和0.5 m，地基厚度取值6.4 m，最终基础中心点的沉降值见表4。

表4 不同网格尺寸下的沉降

可见，网格的精细程度对于沉降的影响较小。网格大小为0.1 m 时的沉降与网格大小为0.5 m 时的沉降，也仅相差1.1 mm，差值率约为2%。值得说明的是，当网格尺寸为0.5 m（与地基分层厚度相近）时，得到的解与分层总和法近乎相同，由此可见分层总和法本质上为一种粗网格有限元（层）法，说明本文的数值方法与分层总和法本质是一样的，图2计算结果略大于分层总和法，可以从有限元理论上进行解释：随着网格的加密，有限元的位移解从下方收敛于精确解。

2.2 算例二：闸室的沉降计算及内力分析

有限深度弹性地基模型借助有限元等数值方法，能克服文克勒地基模型不能考虑地基中的剪应力，以及半无限地基模型只能计算弹性模型及无法分层等缺点[16-17]，具有较强的优势。但其也有自身的弱点，如精细的土体本构模型需要较为复杂的土工试验[18-19]，代价较大，而线弹性模型过于粗糙，计算失真。这里采用本文方法，通过压缩曲线来体现弹性地基的应力变形及对上部结构的影响。通常有限元计算只能得到应力，文献[20]提供了内力的获得方法，使得平面问题通过应力积分得到构件内力。

软土地基上某景观水闸闸室，横断面如图3 所示，地基经概化分3层，由下而上分别为黏土、淤泥质粉质黏土和重粉质壤土。这里仅考虑施工期荷载（主要为结构自重及上部荷载），施工期水位为0.20 m（地基高程为2.90 m）。

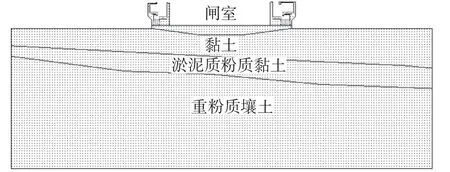
图3 水闸闸室计算模型

采用本文方法进行计算，得到闸室底板的沉降分布及弯矩图如图4 和图5 所示，可见由于闸室横向刚度较大，基底位移较为均匀，最大值约为21.4 mm，两侧荷载基本对称，沉降差最大不到1.5 mm；施工期底板上部受拉，中部弯矩值较大，达到1870 kN·m。

图4 闸室底板底部沉降分布（单位：m）

图5 底板弯矩图（单位：kN·m）

获取地基中的弹性模量分布，随着深度增大，地基应力增大，土体的弹性模量有较大幅度的增长，基底约为4000～5000 kPa，模型底部的弹性模量为72000 kPa，约为基底的16 倍。由于加载后地基中应力增大，其弹性模量较加载前有所增加。在计算闸坝等结构物时，为体现地基弹性对结构应力影响，文献[21]中建议将地基的厚度取为结构物底宽的1～2倍，同时计算实践也显示弹性地基的厚度对计算结果影响较大。这里讨论这一因素的影响，将闸室地基厚度取为（0.25～4.0）d，其中闸室底宽d为39 m，采用本文方法计算，获取底板中心的弯矩及沉降，其结果见图6。

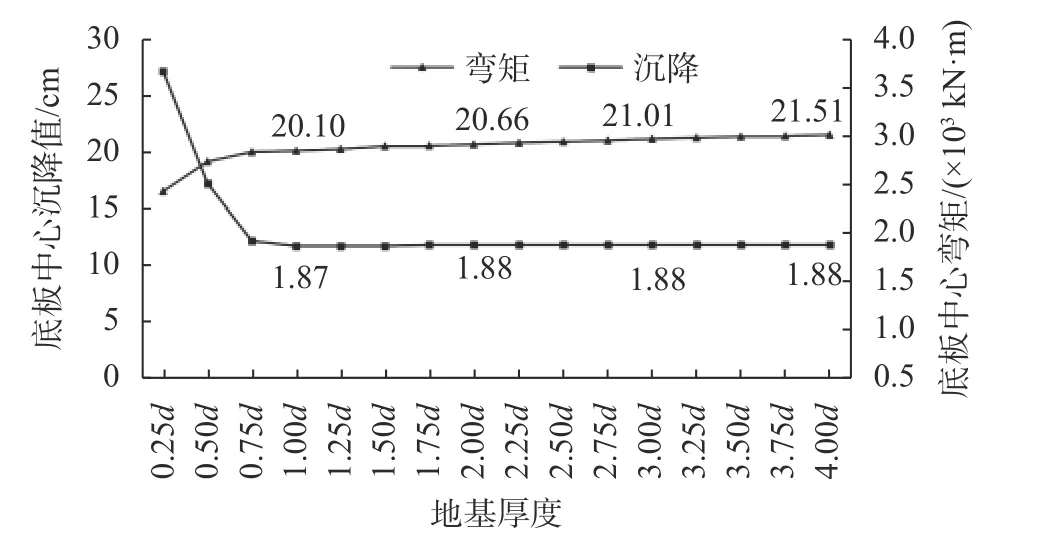
图6 不同地基厚度下的沉降及弯矩

由图6 中的计算结果可见，底板中心的沉降在地基厚度较小的时候（＜0.75d）有较大的变幅，地基厚度取值影响较大，可压缩的地基厚度考虑太少，当地基厚度大于0.75d之后沉降区域稳定，增值为1.41 mm，该值仅占最终结果的约7%；弯矩结果趋势类似于沉降；地基厚度达到1.0d时弯矩值为1.87×103kN·m，与厚度为4.0d的结果所差无几。可见采用本文方法计算可以取得较为理想的结果，当地基深度达到一定深度之后，相比于简单的线弹性模型，本文方法模型的沉降及应力变形计算结果更稳定，不再产生较大的变幅。

3 结论

在传统分层总和法的基础之上，基于有限元法发展了一种地基计算的新方法，该方法以e-p曲线描述地基土体的应力应变特性，通过有限元法计算可迅速的获得地基沉降和地基上梁板的内力。通过具体算例与工程实践验证，得出以下结论：

（1）本文方法与规范推荐的分层总和法本质上相同，但省去了查表、插值等繁杂的手算过程，同时基于电算的有限元数值方法较大程度上提高了计算的速度及精度，具有较好的适用性。

（2）相比于分层总和法每次计算只能获得一个点的沉降值，结果单一离散，本文方法计算结果丰富，可以得到平面上任意一点的沉降，结果全面且直观，可以较为方便地扩展为三维分析，应用前景更为广泛。

（3）与土体的众多本构模型相比，e-p曲线的获取相对容易，并且能直接反映土体的变形特性。本文方法采用e-p曲线描述地基的应力变形特性具有较好的精度，对于弹性地基上结构内力与沉降的计算也更为方便和经济。

本文方法已应用于水工分析系统Autobank，作为分层总和法的发展，以其较强的实用性和精度，具有较好的应用前景。