基于博弈论组合赋权的基坑安全物元评价

苏政凯 张坤勇，2 李福东 简永洲

（1.河海大学岩土工程科学研究所，江苏南京 210024；2.河海大学岩土力学与堤坝工程教育部重点实验室，江苏南京 210024；3.中交二公局第四工程有限公司，河南洛阳 471013）

0 引言

作为城市地下空间开发过程中的重要临时工程，基坑的安全对保障工程的顺利完成和降低施工对周边环境的影响具有重要意义[1]。基坑一旦发生失稳，将对工程本身及周边社会环境产生严重不良影响[2]。随着我国城市地下空间开发规模的扩大，基坑逐渐向“深、广、大”方向发展。复杂地质条件、周边环境和施工管理等导致基坑安全难以仅利用数学及力学知识的准确计算进行评判[3，4]。基坑安全是当前地下工程研究的热点，对其进行多准则多指标的综合安全评价是其中一个重要研究方向。在现有基坑安全评价体系中，各指标权重的确定方法大多较为单一，如层次分析法[5，6]和熵值法[7]。基坑纵深发展带来的不确定因素逐渐增多，单一权重计算方法的适用性下降，评价得出的结论无法反映基坑真实安全状态。利用博弈论对主客观权重进行组合计算，可以获得与实际情况更为契合的赋权结果[8]，再根据物元可拓理论对基坑安全进行综合评价，为工程建设提供有价值的参考[9]。

物元可拓理论基于经典数学方法，用形式化模型在事物不相容的领域间建立起联系，适用于各类矛盾问题的解决[10]。目前，在工程领域物元可拓理论已逐渐被广泛应用于各种复杂实体工程的综合评价。随着物元可拓理论研究的逐渐加深及应用领域的不断拓展，形成了许多以传统物元可拓理论为主体，利用其他算法改进的综合评价体系：吴丹红等[5]采用基于层次分析法的评价指标体系，根据评价指标和对象之间的关联函数和关联度得到地铁车站深基坑安全状态；吴贤国等[6]采用变权思想确定评价指标权重，由贴近度确定基坑风险等级特征值，并利用变权理论对指标进行了敏感性分析；王 伟等[7]对砂卵石地层深基坑开挖评价指标的赋权采用了熵值法；苏广全等[8]结合主客观权重的博弈论组合赋权，对武威市整体洪水风险等级进行评价，并与单一赋权方法的结果进行比较，发现博弈论组合赋权可以降低评价过程中的主观性；邓志秋[9]针对基坑工程等级评价的特点，提出采用正交试验设计方法和有限元分析来确定判断矩阵，然后由层次分析法得出指标权重的方法，针对基坑安全等级评价的特点，采用以指标变动幅度为计算依据的嫡值法来确定权重；李泓泽等[11]对经典域物元和待评物元进行规格化处理，基于变权理论确定了各评级指标的权重，采用非对称贴近度替代最大隶属度准则，提高了物元可拓模型在电能质量综合评价中的适用性。

基坑安全评价需要综合考虑多方面的因素，将物元可拓模型应用于基坑安全评价通常需要进行改进，主要集中在权重值的优化计算及最大隶属度原则的替换，各种改进方法都有其优缺点和适用性。监测指标可以反映基坑的安全状态[9]，基于层次分析法建立了以基坑常规的监测项目为相应准则层，以其累计值或变化速率二者的极大值为基本评价指标因素的安全评价体系。对指标累计值和变化速率的兼顾考虑，可以使整个评价更加符合工程实际中的预警要求；然后利用博弈论组合赋权法对物元可拓模型进行改进，提高基坑安全评价权重赋值的真实性；最后对评价指标进行敏感性分析，找出对评价结果有重大影响的敏感性指标。

1 基本理论概述

1.1 博弈论组合赋权

由于各指标对评价目标最终结果的作用、重要性及影响力是不同的，需要引入定量化的形式来描述各指标对评价目标的重要程度，即权重。在多准则多指标综合评价问题中，确定各指标权重是综合评价的基础，对评价结果的准确性十分重要。指标权重的确定方法大致可以分为两类：主观赋权法和客观赋权法。主观赋权法是评价者基于经验对指标相互间的重要程度进行比较判断，然后通过赋值和计算得到各指标权重的方法。客观赋权法是根据各指标客观数据的差异性，经过处理和综合分析获得各指标的权重[12]。

两类赋权方法各有其优势和局限：主观赋权法基于经验，主观性较强，但在一定程度上具有可继承性且能反映真实情况[9]；客观赋权法由客观数据特征赋权，避免了人为主观的影响，但无法体现各指标之间的相关性，甚至会出现所得权重与指标本身重要程度完全不符的情况[13]。为使对各指标的赋权达到主客观的统一，兼顾既有经验的指标偏好，同时又力争减小主观随意性，可以使用组合赋权的方法进行权重的计算[14]。组合赋权实质上是对多种赋权方法的结果通过计算，得到最终更为客观合理的权重值。

博弈论组合赋权法对主、客观赋权法优点的兼顾具有一定优势，已经在自然灾害风险评价等领域被广泛应用。在博弈论组合赋权中，假定各赋权方法的取值都是最理想的，其目的是寻求组合赋权计算的最优解。最终结果不是由单一权重计算方法决定的，而是由所有计算方法共同实现的。博弈论组合赋权法的基本思想是寻求不同权重计算方法之间的一致或妥协，即最终权重计算结果与各个基本权重计算方法的偏差达到最小[8]。

拟采用博弈论组合赋权的方法进行基坑综合安全评价的权重计算：先进行基于层次分析法的主观权重计算[15]和基于灰色关联分析客观权重计算[16]，再对计算结果进行一致性检验，最后对主客观权重结果进行组合赋权计算[8]。

1.2 物元可拓模型

基于物元理论与可拓集合对物元及其变换进行研究的理论，可用于创造性思维、决策领域、识别与评价、社会科学与物元、人工智能与分析[10]。综合评价涉及多准则、多指标，需要定性与定量的结合，由单项指标得出的结果具有不相容性。不相容问题的解决，是建立科学合理综合安全评估模型的关键。物元分析法可用来求解不相容问题，将物元可拓模型引入到基坑综合安全评价中，可有效解决其中的不相容性，使评价结果更合理[17]。

物元可拓评价模型一般主要包含：（1）根据评价体系和判别标准确定经典域；（2）由经典域可确定相应的节域；（3）由实际客观数据结合经典域形式确定待评价物元；（4）确定指标权重；（5）计算待评物元的关联度和等级特征值。

拟采用非对称贴进度理论进行关联度的计算，避免传统最大隶属度原则易产生最终结果偏差的不足[18]。

2 基坑安全评价模型的构建

2.1 评价体系

以基坑工程中某一施工段作为研究对象，基于常规监测指标构建评价体系，对基坑整体施工段进行评价。根据工程监测技术规范和《基坑工程手册》[19]，将基坑工程评价体系中评语层定为三个安全等级：一级安全，不必采取措施；二级注意，应引起重视，必要时采取相应措施；三级危险，必须采取相应措施。根据各监测项目对基坑安全的影响程度和层次分析法结构选取原则进行准则层和指标层的选取[1，6]，基坑安全综合评价体系如图1所示。

基坑各指标相应的监测点数量一般都比较多，理论上可以将每个监测点的每项监测数据作为一个评价指标，但会导致需要很大的计算量，且引起由于监测点数量布置不合理造成的权重计算不准确。当基坑的某一点发生坍塌或其他事故时，一般认为该基坑处于危险状态，所以基坑安全监控的重点针对各指标的极值。

综合评价体系中的各项指标均为各组监测数据的极值，选取相应规范及文献[6]中的基坑安全判别标准作为评价基础（见表1），表1 中的计算方式已对各指标值进行了无量纲化处理。

表1 各指标等级判别标准

2.2 权重计算

（1）主观权重

采用层次分析法进行计算[15]，运算步骤如下：

1）构建比较矩阵

相比于1-9 标度法，3 标度法的应用不但能够降低权重计算的工作量,同时能减少评价过程中的主观因素、模糊性[20]。对基坑安全综合评价的层次化指标体系中指标层采用3 标度评估尺度构建比较矩阵：

式中：Aij表示为指标元素Ai和Aj两者之间比较得到的评估值，n为评价指标总数。运算规则如下：

2）构建判断矩阵[21]

对比较矩阵A，由式（3）计算各项指标重要程度指数Si。

由式（4）运算得判断矩阵B

3）判断矩阵的一致性检验

式中：CI为一致性指标；λmax为判断矩阵B的最大特征值；n为判断矩阵B的阶数即评价体系中的指标数量。

式中：CR为一致性比例；RI为同阶平均随机一致性指标[22]，对于13 阶的判断矩阵，RI=1.56。

当CR＜0.1时，则该判断矩阵通过一致性检验[20]。

4）计算权重

采用方根法计算判断矩阵B的权重，计算权重的公式为：

（2）客观权重

客观权重基于灰关联分析进行确定[16]，具体步骤如下。

1）确定参考序列，根据专家经验选取各个指标的最优集，记为：

其对应的m组实际数据为：

式中：Xzy为第z组实际数据对应第y个评价指标的实际取值；z=1，2，3，···，m；y=1，2，3，···，n。

2）求X1，X2，···，Xm与X0对应分量之差的绝对值序列，由Δzi=|Xzi-X0i|，得：

3）求Δzi=|Xzi-X0i|的最大值Δmax和最小值Δmin：

4）求关联系数，分辨系数 ξ一般取0.5：

关联系数矩阵：

5）计算比较序列相对于参考序列的关联度：

6）计算权重：

（3）组合赋权

1）权重的一致性检验

在组合赋权前，需要进行各权重的一致性检验。采用了2 种赋权方法计算，可以用距离函数描述赋权方法的结果一致性程度[8]，即

式（19）中r1i表示主观赋权，r2i表示客观赋权。d(r1ir2i)≤0.4时，可以认为满足一致性要求。

2）由L种赋权方法构成基础权重向量集rk=[rk1,rk2,...,rkn](k=1,2,···,L)，则组合权重向量为：

式中：γk为线性组合系数。

3）线性组合系数 γk的计算

博弈论中需要对线性组合系数进行优化，使得结果向量r与各方法赋权结果向量rk离差最小，即依据式（21）可以求解最优权重系数：

由矩阵微分性质，可将式（21）展开可得线性方程式（22），求解方程组便可获得最优权重系数：

求得的最优权重系数向量为γ*=[γ1,γ2,···,γL]，利用式（23）进行归一化处理。

将归一化处理得到的最优权重系数代入式（24），即可得到博弈论组合赋权的最终结果。

2.3 经典域、节域和待评物元确定

（1）经典域

式中：Rv为一个物元，由基坑安全级别、安全评价指标和指标取值范围构成；Nv为第v个评价类别，即基坑安全性级别为v；Cj为第j个基坑安全评价指标；Vvi为Cj所确定的取值范围，即经典域，Vvi=＜avi,bvi＞,(i=1,2,···,n)。

（2）节域

式中：P为基坑安全评价指标的全体；Vpi为P关于Ci确定的取值范围，即P的节域。

（3）待评物元

对待评的基坑区域t，将实测待评数据通过物元形式表示出来，即可得到待评基坑区域物元Rt为：

2.4 非对称贴近度计算

非对称贴进度可表示为：

式中：ρv为非对称贴近度；Dv(vi)=|vi-(avi+bvi)/2|-Dv反映了待评基坑区域物元Rt与基坑安全评价标准（经典域）Vvi之间的距离；n为评价指标的个数；W(i)为各指标的组合权重。

2.5 确定基坑风险等级

为避免最大非对称贴近度差值较小导致实际应用时的不方便，对贴近度 ρv进行标准化处理[23]，得到标准化贴近度

2.6 等级变量特征值计算

待评基坑区域物元Rt的等级变量特征值t*为：

通过t*可以判断待评基坑区域物元Rt偏向相邻安全等级的程度，等级变量特征值t*越大，表明在隶属当前安全等级的同时，其偏向相邻安全等级的程度越高。

3 工程实例

基于上述理论，按照图2 所示流程，对处于长江漫滩某地铁车站基坑进行安全评价。基坑宽度为21.7 m，顶板覆土约为3.059 m，为地下两层结构，基坑深度为17.8 m，施工工法为明挖顺做法。基坑主要位于淤泥质粉质黏土层，围护结构为地下连续墙（厚800 mm）+内支撑的形式，其中第一道支撑为混凝土支撑，其余为钢支撑。基坑周边存在较多既有重要建筑，地下管线密集，因此对基坑的安全要求较高，基坑施工现状如图3 所示。

图2 基坑安全评价流程图

图3 基坑开挖现状

理论上，选取的实测数据样本数量越多，评价结果的准确度越高。为简化计算，选取了连续10 天的实测数据进行客观权重的计算，以最后1 天的实测数据为例进行了贴近度和等级变量特征值的计算，进而对基坑安全状态进行判断。

3.1 物元模型建立

表1 评判标准确定评价指标的经典域见式（31）。

节域和待评物元，见式（32）。

3.2 权数计算

专家依据经验针对该基坑的评价指标进行重要程度的对比，然后基于层次分析法计算获得各评价指标的主观权重；由灰关联分析法计算得到客观权重；并利用式（21）-式（24）进行博弈论组合赋权计算得到组合权重，结果见表2。

表2 各指标权重计算结果

3.3 等级评价结果

根据非对称贴近度理论，由式（28）、式（29）求得待评基坑区域的非对称贴近度及基坑安全评价结果见表3。

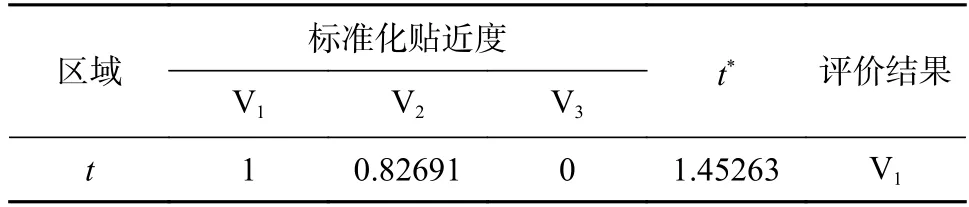
表3 基坑安全评价结果

由上述结果可知：基坑安全等级为V1（安全），等级变量特征值为1.45263，待评基坑安全等级属于偏向V2的V1类，基坑评价结果与当天现场相关情况相符。

3.4 指标敏感性分析

选取了13 个评价指标作为安全评价模型基本因素。为了获取对综合评价结果影响较大的敏感因素，对各评价指标对评价结果的影响进行敏感性分析。通过研究评价指标取值变化对综合权重值与综合评价值即等级变量特征值产生的波动影响，可确定各评价指标对综合权重值与综合评价值的敏感性，采用标准差对各评价指标的敏感性进行量化处理[6]。

当13 个评价指标取值分别以±10%、±20%、±30%、±40%的趋势变化时，上述2 个目标变量的变化规律分别如图4 和图5 所示，然后计算对应的标准差，并根据标准差进行排序，如表4 所示。

表4 等级变量特征值的变化幅度标准差

图4 权重随指标值变化情况

图5 等级变量特征值随指标值变化情况

由图4 可知，对于部分评价指标，与其对应的权重呈现随着其评价指标取值的增大而减小的趋势，如C1、C3、C4等；部分评价指标呈现权重随评价指标取值的增大而增大的趋势，如C5、C9等；还有其他评价指标随评价指标取值的增大，权重呈现先增大再减小的趋势，如C2、C11。各项评价指标相同变化幅度对应权值的变化幅度各不相同，且不同评价指标的权重变化规律存在明显的差异，体现了评价过程中各评价指标的主动参与[24]。

由图5 可知，各评价指标的等级变量特征值整体上随着其取值的增大而增大，各指标变化引起的等级变量特征值变化幅度差异较明显，各评价指标对综合评价值的敏感性各不相同。评价指标取值的变化对等级变量特征值有一定影响，当其取值位于不同范围时，其变化对于特征值的影响规律趋于一致，但影响程度大小略有不同。一些指标的取值在一定范围内变化，对特征值结果影响很小，可以忽略。

从表4 中的标准差，即可得知各指标参数的敏感性强度的相对程度,其中C12、C4、C1是权重的敏感性指标,同时也是特征值的敏感性指标。由上述分析,可以得到权重与等级变量特征值受评价指标取值不同影响的变化规律,并得出上述指标是对该基坑安全状态有重大影响的敏感性指标。

4 结论

（1）将博弈论组合赋权理论与改进物元可拓理论相结合，构建了基坑综合安全评价模型，该模型兼顾了主客观因素，体现了评价指标权重的真实性，增加了评价指标的主动参与。采用非对称贴近度准则可以有效避免评判过程中因信息损失引起结果存在偏差。

（2）运用该模型对位于长江漫滩某地铁车站基坑安全状态进行评价，得出该基坑安全等级为V1级（安全）且偏向于V2级（注意），评价结果与施工情况相符。由敏感性分析的结果，得出“围护结构墙顶水平位移的变化速率”、“围护结构墙顶竖向位移的累计值”、

“地下水位变化累计值”是影响该基坑安全的敏感性指标，需要对其加强监控。

（3）基于博弈论组合赋权的物元可拓基坑安全评价模型，能够深入分析各个指标对目标层的影响，进而判断出基坑的安全状态，并找出影响基坑安全的主要因素，为基坑施工的监测与管理提供参考，为基坑安全评价问题提供新思路。