基于合作协同进化算法的航迹冲突解脱研究
徐 满,胡明华,周 逸,张 颖
(南京航空航天大学 民航学院,南京211106)
随着经济的不断发展,亚太地区将成为航空客运量增长的主要动力,中国将在2022年成为全球第一大航空运输市场[1].根据国际航空运输协会的报告,到2034年,往返亚太地区和在亚太地区内部的航线每年将增加18亿人次,总体市场规模将达到29亿.与其他地区相比,规模将增加到全球客运量的42%,年平均增长率为4.9%,与中东并列最高[2].随着空中交通需求的不断增长,空中交通的拥堵情况越来越严重,航空器之间的潜在冲突大大增加,导致空中交通管制员工作负荷的增加,危及空中交通安全[3].冲突解脱旨在根据航空器的飞行计划解决航空器在运行过程中的潜在冲突,是确保航空器安全运行的一项关键技术.
航空器的冲突解脱问题是一个大规模组合优化问题,共同使用空域资源使得航空器之间相互耦合[4].已有大量文献的研究航空器的冲突解脱方式,包括调整航空器起飞时刻[5]、调整航空器的飞行速度[6]、修改航空器的水平航迹[7]以及高度层分配[8]等方式及其组合[9].但是,目前传统的基于扇区的空中交通系统已经不能完全满足交通量未来的增长需求[10].大量的研究集中在战术阶段的冲突解脱问题,战术冲突解脱能在有限的范围内解决局部冲突,但是由于航空器之间的耦合关系,短期内的冲突解脱可能会产生“多米诺骨牌”效应,使得冲突解脱一直处于被动状态,危及空域安全.例如,采用地面等待策略时,已经延误了的航空器仍然有可能继续等待其他航空器以满足空域的容量要求[5].而战略阶段的冲突解脱可以从全局角度解决航空器之间的潜在冲突,降低航空管制员的工作量,从而提高空域容量,缓解交通压力.
4D航迹的运用以及TBO的提出被认为是未来空中交通管理的运行基础.4D航迹将航空器航迹定义为三维空间加上时间,随着运行技术的不断发展,4D航迹可以有效降低航空器运行过程中的不确定性.这就为在一个较长时间范围内解决航空器之间潜在冲突提供了技术支持,使得在战略阶段解决冲突成为可能.因此,基于4D航迹,综合优化给定空域范围内所有航空器的飞行计划被认为是未来应对空中交通需求挑战的关键技术[11].
在对航空器进行冲突解脱时,可以分为经典冲突解脱方法和机器学习冲突解脱方法.经典冲突解脱方法由于问题模型的复杂程度,常采用启发式算法求解.模拟退火算法及其改进[9,12-14]获得了广泛的应用.Dai[9]等人结合模拟退火算法,设计了一个均匀高度层策略,将航空器均匀分布至各个可用的高度层.但是该方法复杂度较高且需要较大的计算量.为了降低问题的复杂度,引入滑动时间窗来降低问题的维数,从而获得可行解[5].降低问题的维数可以降低问题的复杂度,提高算法的效率.Guan[4]等人首次将合作协同进化算法(Cooperative Coevolution Evolutionary Algorithm,CCEA)应用到航班冲突解脱问题中.CCEA采用分而治之的思想,将一个大规模组合优化问题分解成若干个子问题,从而降低问题的维数,各个子问题采用特定的进化算法优化得到部分可行解,通过各个小组之间的合作进化获取全局可行解.在CCEA的框架下,分组策略对算法效率具有重大影响.常见的分组策略有固定分组、均匀分组、随机分组[15]、基于先验知识分组[4]等,各种分组策略有各自的适应场景[16].其中,基于先验知识的分组策略,充分考虑航空器之间的冲突关系,将相互影响的航班分入同一小组内进化,充分发挥了先验知识的优势,算法具备良好的效果.采用机器学习[17]进行冲突解脱近几年得到了迅速地发展,但是其多适应于战术阶段的冲突解脱,在战略阶段的大规模场景下的应用需要进一步的研究.
在实际运行过程中,空中交通管制员往往会在冲突数量和航空器航迹调整量之间寻求一个很好的平衡.针对这一目的,Yan Su等人[18]以最小化冲突数量和最小化航迹调整量为目标,在TBO概念下采用多目标文化基因算法求解多目标模型.在求解全国范围内的无冲突航迹时,问题的复杂度较高,算法求解效率下降明显.冲突解脱模型中目标具有多样性,Mateos等人分析了六种不同的目标函数,包括最小化航空器机动次数和幅度、最小化冲突风险、最小化航班延误、最小化分离点偏差和最小化航空器机动频率[8].CCMOEA[10]同样被应用于冲突解脱问题,在协同进化算法的框架下,采用MOEA/D[19]进行各个小组的内部优化.但正如作者在文中指出一样,算法的求解效率可以进一步提高.
本文从空中交通管理的角度出发,综合考虑最小化冲突以及解冲突所导致的航迹调整量,建立起飞前战略航迹冲突解脱多目标优化模型.为快速求解模型,设计IBCCMOEA进行模型求解,在协同进化算法的框架下采用动态分组的方法降低问题维度,利用NSGA-II[20]进行组内优化.在组内优化时根据超体积(Hyper Volume,HV)指标选择协同解,从而进一步提高算法的收敛速度.采用中国航路网繁忙时段真实数据进行仿真验证,将所提算法与使用较多的多目标优化算法进行对比,包括NSGA-II,MOEA/D以及CCMOEA,实验结果表明,所设计的算法在收敛速度以及求解结果上均具有良好的性能.
1 问题模型
本文研究巡航状态下的冲突解脱问题,因此航迹起终点为爬升和下降顶点.假设空域中有n架航空器,F=(f1,f2,f3,…,fn),按照航班计划沿着特定的航路飞行,航空器处于巡航状态,以恒定的巡航速度飞行.
基于四维航迹的冲突解脱可以被定义为:给定航班飞行计划及航路网络,尽可能减少航空器之间的飞行冲突并产生较少的调整量.在进行航空器的冲突解脱的过程中,应满足空域容量及航空器性能等因素的限制.在4D航迹条件下,航空器f的航迹由一组4D航迹采样点组成:
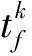
1.1 多目标航迹规划决策变量及约束条件
本文采用调整航空器起飞时刻以及高度层两种方式解决航空器之间的潜在冲突.在时间维度,冲突解脱表现为与航班fi相对应的起飞时刻δi的调整;而在空间维度,表现为与航班fi相对应的飞行高度层li的调整.决策变量表示为u:=(δ,l),其中δ为n个航班的起飞时间调整矢量,l为n个航班的高度层调整矢量,分别表示如下:
δ:=(δ1,δ2,δ3,…,δn)
l:=(l1,l2,l3,…,ln)
决策变量必须满足以下约束:
1)地面延误约束:由于不能将航空器的起飞时间推迟的太久,∀fi∈F,i=1,2,…,n,其对应的地面延误ΔGHi必须保持在离散化的区间[0,ΔTGH]中,所有可能的延误集合ΔGHi定义如下:
(1)
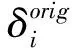
2)高度层分配约束:巡航状态下的高度层分配受到航空器性能的限制,也应受到约束.∀fi∈F,i=1,2,…,n,所有可能的高度层偏移量集合ΔFLi定义如下:
(2)

1.2 目标函数
冲突解脱的首要目标是解决航空器之间的潜在冲突,实现冲突最小化.目标一为最小化航班之间的冲突数量,表示如下:
(3)
其中:C(w(δi),w(δj),li,lj)为布尔变量,表示航迹采样点之间的冲突关系.
在冲突解脱的过程中,航空器需要做出相应的机动来规避冲突.为了尽可能减少与其他航空器之间的冲突,可以对航空器的初始航迹做出大幅度调整,但是会产生额外的飞行成本.因此,目标二为最小化航迹调整成本(Total Trajectory Amendment Cost,TTAC),TTAC由地面延误成本(CostGH)、高度层分配成本(CostFL)构成,表示如下:
minObj2=TTAC=λGH×CostGH+λFL×CostFL
(4)
其中:λGH与λFL分别表示地面延误与高度层分配成本系数.由于地面延误成本与高度层分配成本量纲不同,因此先进行归一化再相加.地面延误成本与高度层分配成本定义如下:
(5)
(6)
其中:F为航班集合,l为可用飞行高度层集合,δ为起飞时刻集合.
2 基于超体积的多目标合作协同进化算法
CCEA最初由Potter[22]提出,其主要思想是采用特定的分组策略将一个大规模优化问题分解成多个小规模优化问题,从而降低问题的复杂度.在协同进化算法中,各个子问题采用相应的进化算法分别进行组内优化,通过个体与其他子种群代表个体的协同评价获得子种群的适应度值,最优解通过子种群之间的协同进化得到.CCEA及其改进在航空规划领域已有过大量成功的应用[4,10,23].
当将该框架应用于多目标优化时,影响算法效率的一个关键因素为选择子种群代表性个体的方法.常用的一种选择方式为从各个子种群的Pareto解集中随机选择一个非支配解,但是与其他子种群代表个体相结合形成完备解时却有可能产生较差的解[24].本文采用一种基于超体积指标的选择策略,根据个体贡献度选择代表性个体.
在分组时,采用动态分组策略将相互关联的航空器放入同一小组;组内优化时,采用NSGA-II结合自适应遗传算子进行优化,选择子种群代表性个体时采用基于超体积指标的选择方法,算法框架如下:

Algorithm1:IBCCMOEA
-------------------------------------------
Input:Initial solution,MAXgenerations,maxgenerations
Output: IBCCMOEA solution
// Main procedure
1:Initialize the initial solution to generate the initial population;
2:fori=1:MAX generationsdo
3:Evaluate all the individuals in the population and compute the non-dominated solution;
4:Select an objective vector based on the HV indicator;
// Cooperative co-evolution
5:Decompose the objective vector intomilow subcomponents based on the dynamic grouping
6: strategy;
7:Set;j=1;
8:whilej≤mido
9:forK=1:maxgenerationsdo
10: Initialize thejthsubcomponent;
11: Select theoffspringkbased on the HV indicator;
12: Use the adaptive crossover and mutation strategy to obtain theoffspringk+1;
13:endfor
14:j=j+1;
15:endwhile
16:endfor

2.1 动态分组策略
分组策略是影响IBCCMOEA效率的关键因素之一,本文采用动态分组策略,根据航空器之间的冲突关系进行分组.为了表示航空器之间的冲突关系,定义一个矩阵C来表示航空器之间是否存在冲突:
(7)
矩阵C是一个n×n矩阵,第i行,第j列表示航空器fi,fj之间的冲突关系,即:
(8)
当任意两架航空器之间没有冲突时,采用均匀分组策略将航空器分成数量相等的m组.
当存在相互冲突的两架航空器时,即:∃i≠j,Cij=1,此时根据航空器之间的冲突关系将相互影响的航班放入同一小组之内:
(9)
其中:nk表示第k组的航班数量.在此种分组策略下,同一小组内的航班之间一定是相互影响的,不同小组之间的航班不存在相互影响,即:
∃fi,fj∈groupk,Cij=1.
∀fi∈groupk,fj∈groupl,Cij=0.
(10)
2.2 子种群优化
2.2.1 染色体结构
在用IBCCMOEA求解模型时,采用整数编码的方式,将航班起飞时刻及高度层按照航班序号进行排序并编码.染色体结构如图1所示.
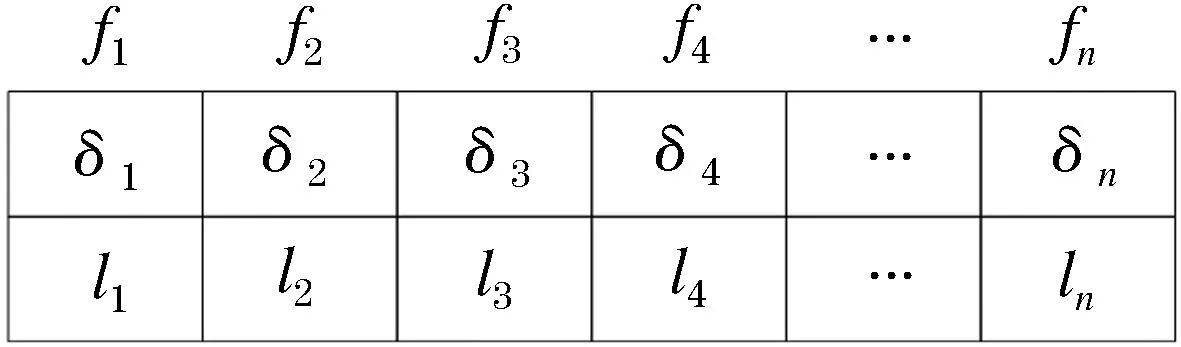
图1 染色体结构Figure 1 Chromosome structure
2.2.2 子种群初始化
在初始化种群时,根据航空器当前的冲突数量,采用轮盘赌选择,优先选择冲突数量较多的航空器,调整起飞时刻的概率为PGH,调整高度层的概率为PFL,PGH+PFL=1.
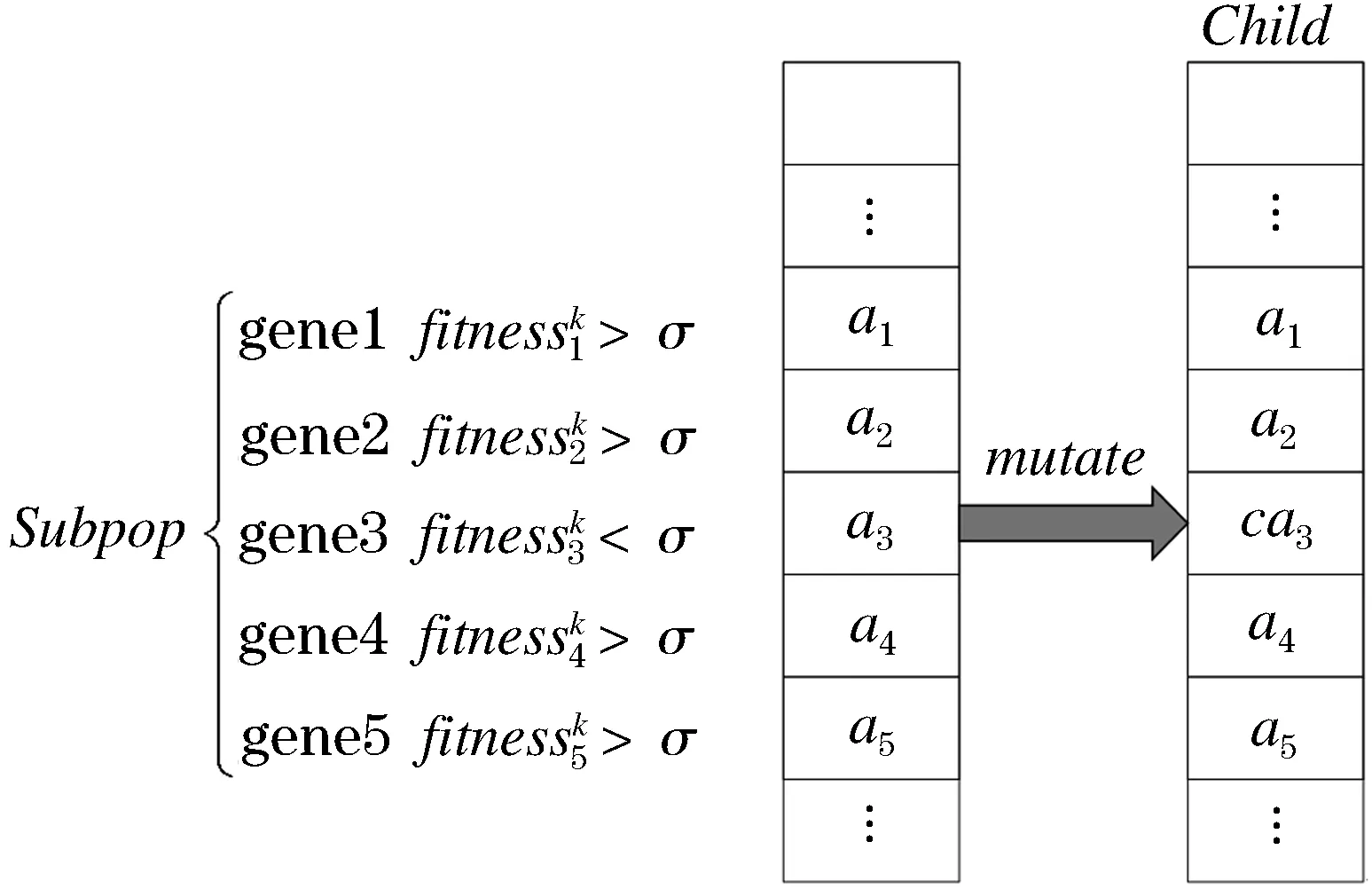
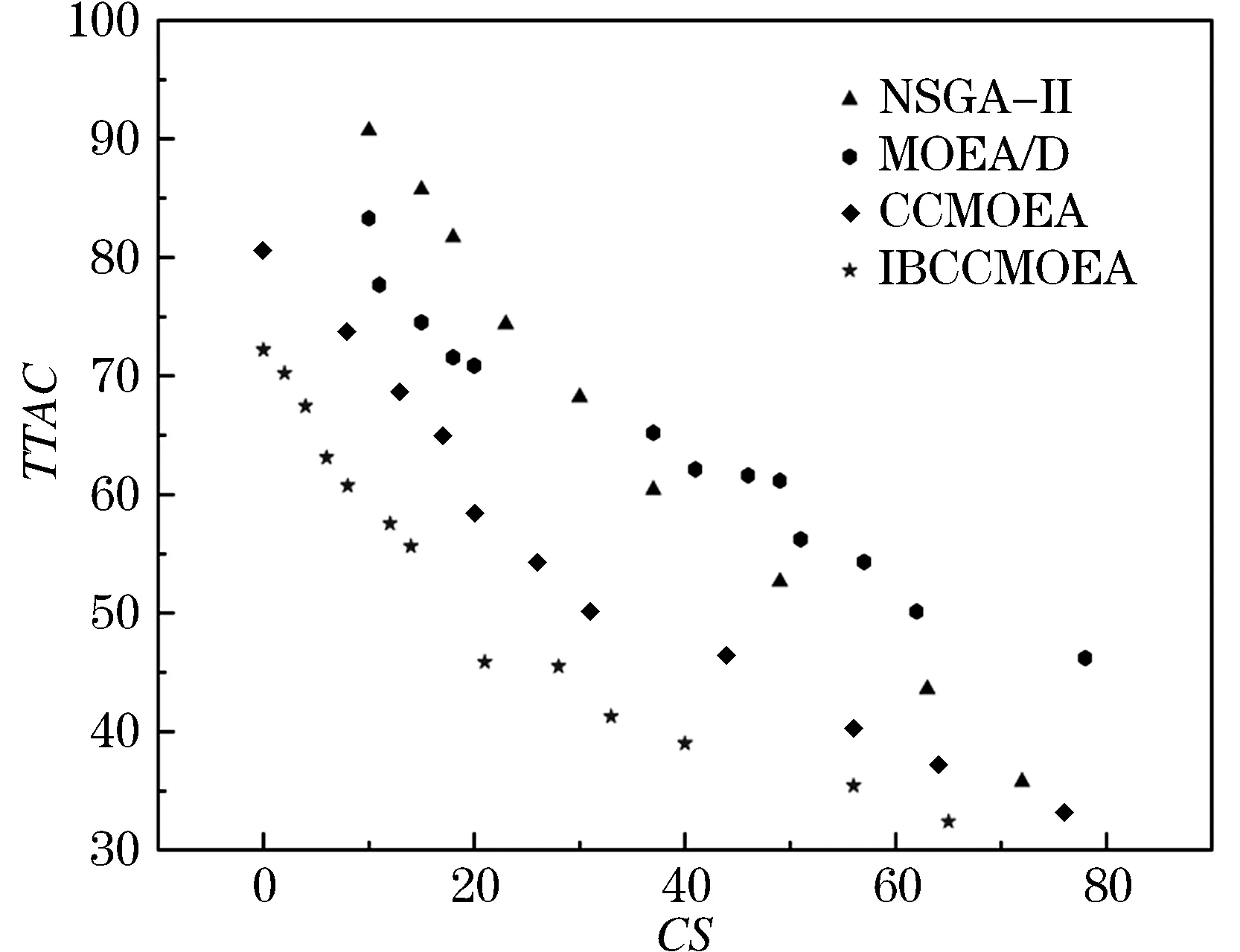
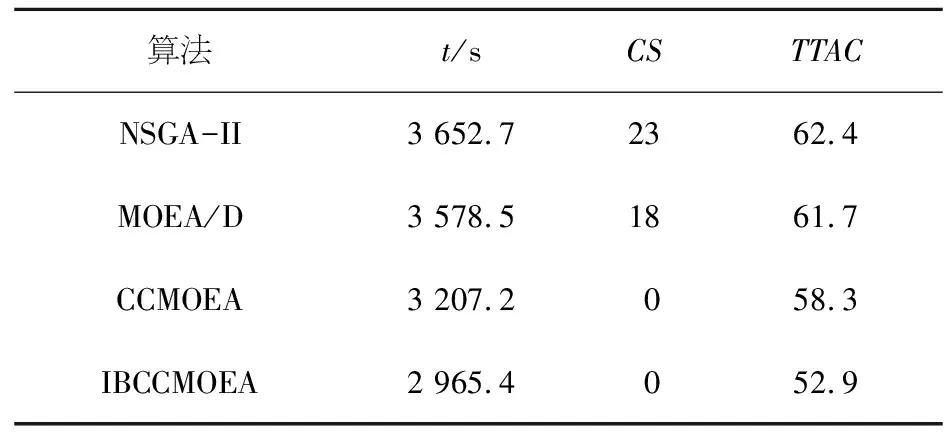
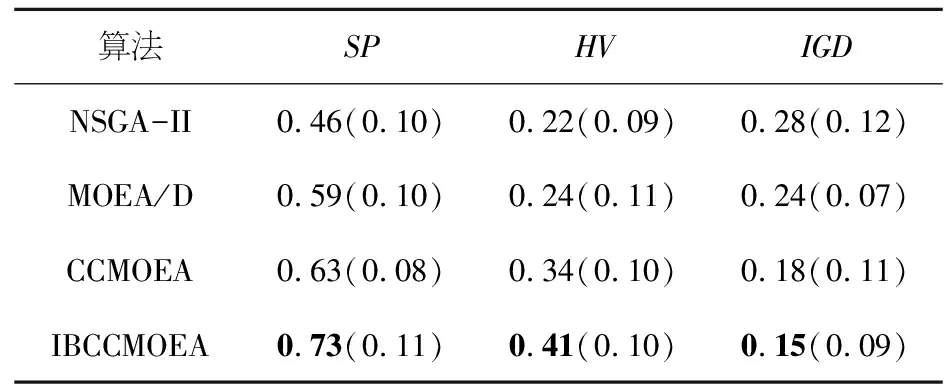
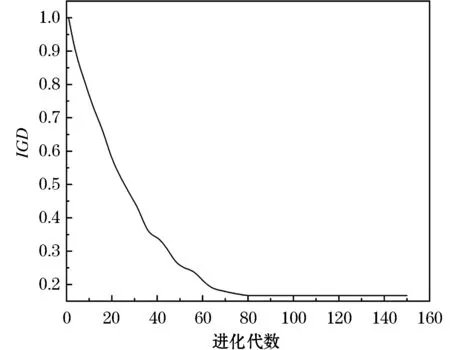
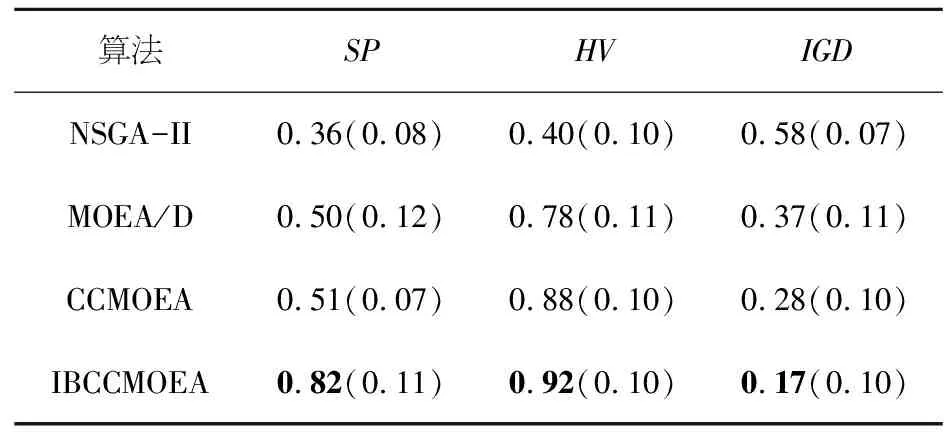
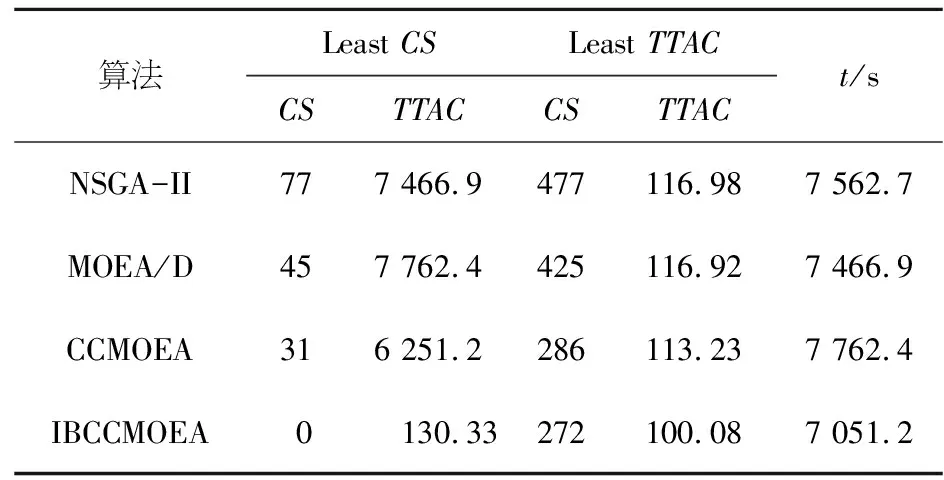
生成随机数r,当时0 图2 子种群初始化Figure 2 Sub-population initializing 2.2.3 基于超体积的选择机制 HV[25]是一个由维数为n的点集合所包含的n维空间,应用于多目标优化时,将解的n维目标值作为该空间的点来计算,即通过非支配解P在目标函数空间中的体积求得超体积.∀pi∈P,根据参照点R生成一个超立方体vi,pi为超立方体vi的另一个对角,计算方式如下: (11) 在MOEAs中,使用HV作为选择策略是根据个体对总体的HV贡献度,优先选择对前沿解的HV贡献度较大的个体,属于总体P的个体pi的HV贡献值计算方式如下: Δspi=S(P,R)-S(P{pi},R) (12) 在双目标优化时,该计算过程如图3所示.本文在选择各个子种群代表性个体时,首先计算种群中个体的适应度,对其进行非支配排序,其次计算个体对前沿解的HV贡献度,选择对前沿解的HV贡献度较大的个体. 图3 超体积贡献值Figure 3 Hyper volume contribution 2.2.4 自适应交叉算子 自适应交叉算子根据航班的局部适应度确定,本文采用的局部适应度算子综合考虑了目标一与目标二,局部适应度计算方式如下: (13) caj=floor(εaj+(1-ε)bj) (14) 其中:floor为向下取整,ε为线性重组系数.自适应交叉算子原理图如图4所示,交叉概率为Pc. 图4 自适应交叉算子Figure 4 Adaptive crossover operator 2.2.5 自适应变异算子 当航空器的局部适应度值越高时,表明该航空器按当前飞行计划会产生更少的冲突数量和航迹调整量.在本文采用的自适应变异算子中,当子种群k中的第j架航空器的局部适应度值小于σ时,发生变异的概率为Pm,自适应变异算子如图5所示. 图5 自适应变异算子Figure 5 Adaptive mutation operator 首先采用中国航路网络2019年6月8日9点至11点442架航班的小规模算例对模型参数进行分析,在Matlab R2019a平台上运行.所用数据包含7 684个航路点,93个起降机场.航空器的初始飞行计划有237个潜在飞行冲突.巡航阶段航空器的飞行速度v设置为980 km/h,允许的最大延误ΔTGH为30 min,调整航空器起飞时刻的时隙设置为2 min;遵循“东单西双”的原则,垂直方向上每300 m划分为一个高度层,高度范围为8 900~11 600 m,允许的最大高度调整量ΔLFL为1 200 m;采用等时间间隔对航迹点进行采样,航迹采样点时间间隔τ为20 s. 为了验证IBCCMOEA算法在冲突解脱中的高效性,对于模型中的各项参数进行灵敏度分析,选定最优参数组合;分别采用NSGA-II,MOEA/D,CCMOEA三种算法进行求解及比较. 3.1.1 参数灵敏度分析 本文采用地面延误及高度层分配两种方式进行冲突解脱,在1.2节中两种冲突解脱方式所产生的成本通过式(4)进行加权作为本文的目标函数之一,同时依概率选择冲突解脱方式.令λGH+λFL=1,PGH+PFL=1.在对λGH和λFL进行灵敏度分析时,PGH与PFL采用默认值0.5;在确定了最优的λGH和λFL后,将其应用到PGH与PFL的分析中.独立重复试验10次,给出在不同系数下Pareto前沿的HV作为依据,如图6所示. 图6 λGH,λFL,PGH,PFL灵敏度分析Figure 6 λGH,λFL,PGH,PFL sensitivity analysis 表1 模型参数设置Table 1 Parameter settings of model 除了对模型中的参数进行灵敏度分析,算法中的四个参数:交叉概率(Crossover rate,Pc),变异概率(Mutation rate,Pm),最大进化代数(Generations)和种群规模(Population size)同样需进行灵敏度分析.在分析当前参数时,其他参数设置为默认值0.9,0.05,80,150,获取的最佳参数用于后续算法比较[26]. 在灵敏度分析过程中,HV,反转世代距离(Inverted Generational Distance,IGD)和散度(Spread,SP)[27]用于衡量该参数条件下算法性能.图7为IBCCMOEA基于10次重复独立运行所得到的结果.HV,SP值越大且IGD值越小,说明在该参数条件下算法性能越优异.其余三种算法灵敏度分析方法相同,最优参数组合如表2所示. 表2 算法参数设置Table 2 Parameter settings of algorithms 图7 参数灵敏度分析(显著性水平5%)Figure 7 Parameters sensitivity analysis(significant level at 5%) 3.1.2 算法高效性与收敛性 图8给出了四种算法对应的Pareto前沿,可以看出,IBCCMOEA优化后得到的Pareto前沿优于其他三种算法,在冲突解脱以及航迹调整成本方面表现出优越的性能. 图8 小规模算例Pareto前沿Figure 8 Small-scale case pareto front 为了证明算法冲突解脱的高效性,给出NSGA-II,MOEA/D,CCMOEA,IBCCMOEA在442架航班冲突解脱过程中每一代的Pareto前沿平均冲突数量变化趋势图,如图9所示.表3为四种算法的运行时间、冲突数量及对应的航迹调整成本. 表3 运行时间、CS及TTAC对比Table 3 Running time, CS and TTAC 图9 平均最小冲突数量Figure 9 Average minimun total conflict 由图9可知,IBCCMOEA对于无冲突解的搜索效率最高,在进化过程中其冲突解脱的速度最快.对比NSGA-II与CCMOEA,采用了合作协同进化算法框架的CCMOEA具有更高的效率,同时还可以得到无冲突的可行解,这是因为在引入了合作协同进化的框架之后,将相互影响的航空器放入同一小组进行分别优化,避免在冲突解脱时对两个相互没有影响的航空器进行调整,浪费计算资源.通过表3中的对比可知,在收敛速度上,IBCCMOEA比CCMOEA快了约7.54%,同时IBCCMOEA产生的航迹调整成本减少了约9.62%. 因此,在引入了HV进行选择时,算法的性能可以进一步提高.这是因为CCMOEA在选择代表子种群时,从子种群中的Pareto集合中随机选择一个解作为代表,与其他代表形成完备解时会产生较差的解;而在引入了超体积指标作为选择依据时,在子种群的Pareto解集中,根据各个非支配解的HV贡献度选择代表,更好的考虑了综合性,因此提高了冲突解脱的效率. 分别计算Pareto前沿的SP,HV和IGD,如表4所示,为各个算法10次独立重复试验中各项指标的平均值及标准差. 表 4 小规模算例算法性能对比Table 4 Performance comparision between algorithms in small-scale case 由表4可知,IBCCMOEA在各项指标上均优于其他各种算法.其中,SP的值最大,表明算法的分布更均匀;HV值最大,表明算法的综合性较好;IGD值最小,表明距离参考集越近,因此算法的收敛性要优于其他三种算法.其IGD随进化代数的变化趋势如图10所示.由图可知,算法最终收敛. 图10 IGD趋势图Figure 10 IGD trend 为了验证所提算法在大规模场景下的适应性,对于1 014架航班真实飞行数据进行仿真验证.所用数据航空器经过的航路及冲突位置如图11所示,其中包含150个起降机场,19 624个航路点.航空器初始航迹中的冲突数量为747个.在大规模算例中采用允许的航班最大延误ΔTGH为60 min,允许的最大高度调整量ΔLFL为1 200 m. 图11 大规模算例Pareto前沿Figure 11 Large-scale case pareto front 在大规模冲突解脱场景下得到的Pareto前沿的SP,HV及IGD平均值及其标准差,如表5所示. 表5 大规模算例算法性能对比Table 5 Performance comparision between algorithmsin large-scale case 由表5可知,在大规模场景下,IBCCMOEA的优化结果仍然具有优势,在大规模场景下具有实用价值. 图11为所采用的四种算法分别优化得到的Pareto前沿,均基于10次独立重复实验.由图11可知,IBCCMOEA的优化效果更好,其优化得到的Pareto前沿完全支配其他三种算法.两种经典的多目标优化算法NSGA-II与MOEA/D,优化速度较慢且优化出的结果不理想.在引入了合作协同进化框架后,CCMOEA在降低冲突数量上更高效,但提高了算法的复杂度.在此基础上,为了克服CCMOEA随机选择代表个体可能产生较低质量的解的缺点,引入了超体积指标作为选择机制,优化结果表明能有效提高算法效率.因此,所采用的算法优点为:采用了协同进化策略提高了算法的搜索能力;采用了基于超体积指标的选择策略及自适应遗传算子,提高了算法的搜索效率. 表6为四种优化算法的Pareto前沿中最小冲突数量及最小航迹调整量对应的解,同时给出了对应的求解时间.IBCCMOEA的冲突解脱效果优于其他算法,可以得到无冲突的解,航迹调整成本也低于其他算法,求解速度也在可以接受的时间范围之内. 表6 1 014架航班Pareto前沿最小冲突和最小航迹调整成本对应解Table 6 Non-dominated solutions with the least CS and the least TTAC for 1014 flights 图12为四种算法优化结果冲突数量最小的解,其对应的航空器地面延误及高度层分配的分布图.其中,IBCCMOEA算法对应的解,62%的航空器没有产生延误,68%的航空器遵循着初始飞行高度层;航空器的延误主要分布在10 min之内,超过30 min的延误只有0.4%的航班;航空器飞行高度的调整也主要分布在600 m之内.随着调整量的增大,航空器所占比例逐渐减小,证明本文采用的算法不仅冲突解脱效率高,而且产生的航迹调整成本也较低. 图12 地面延误及飞行高度调整量分布图Figure 12 Distribution of ground delay and flight level adjustment 本文研究了航空器运行中的冲突解脱问题.首先根据问题特点,建立了基于冲突数量和航空器航迹偏移成本的双目标优化模型;其次采用一种基于指标的多目标合作协同进化算法求解该问题.冲突解脱问题是一个大规模组合优化问题,为了提高求解效率,采用动态分组方法将航空器按照冲突关系分组,将该大规模问题分解为若干了子问题,该协同策略提高了算法的搜索能力,针对协同进化过程中,子种群代表性个体的选择问题,采用了基于超体积指标的选择策略,优先选择超体积更大的个体,该策略对提高算法搜索效率有效.为了验证算法的优势,分别采用小规模和大规模算例,将IBCCMOEA算法与NSGA-II,MOEA/D,CCMOEA进行对比,结果验证了本文算法的性能优势. 下一步的工作主要集中在对更多样化的冲突解脱方式以及如何进一步结合解冲突方式的特点进行算法设计从而提高算法求解效率上:冲突解脱方式除了本文采用的调整航空器起飞时刻以及高度层优化分配,还可以考虑航迹的水平调整、高度层和速度在不同航段的分别优化;同时,加入对航迹预测不确定性的考虑,使得模型更符合实际运行情况,所生成的解冲突方案在存在不确定性的运行环境下具备较强的鲁棒性.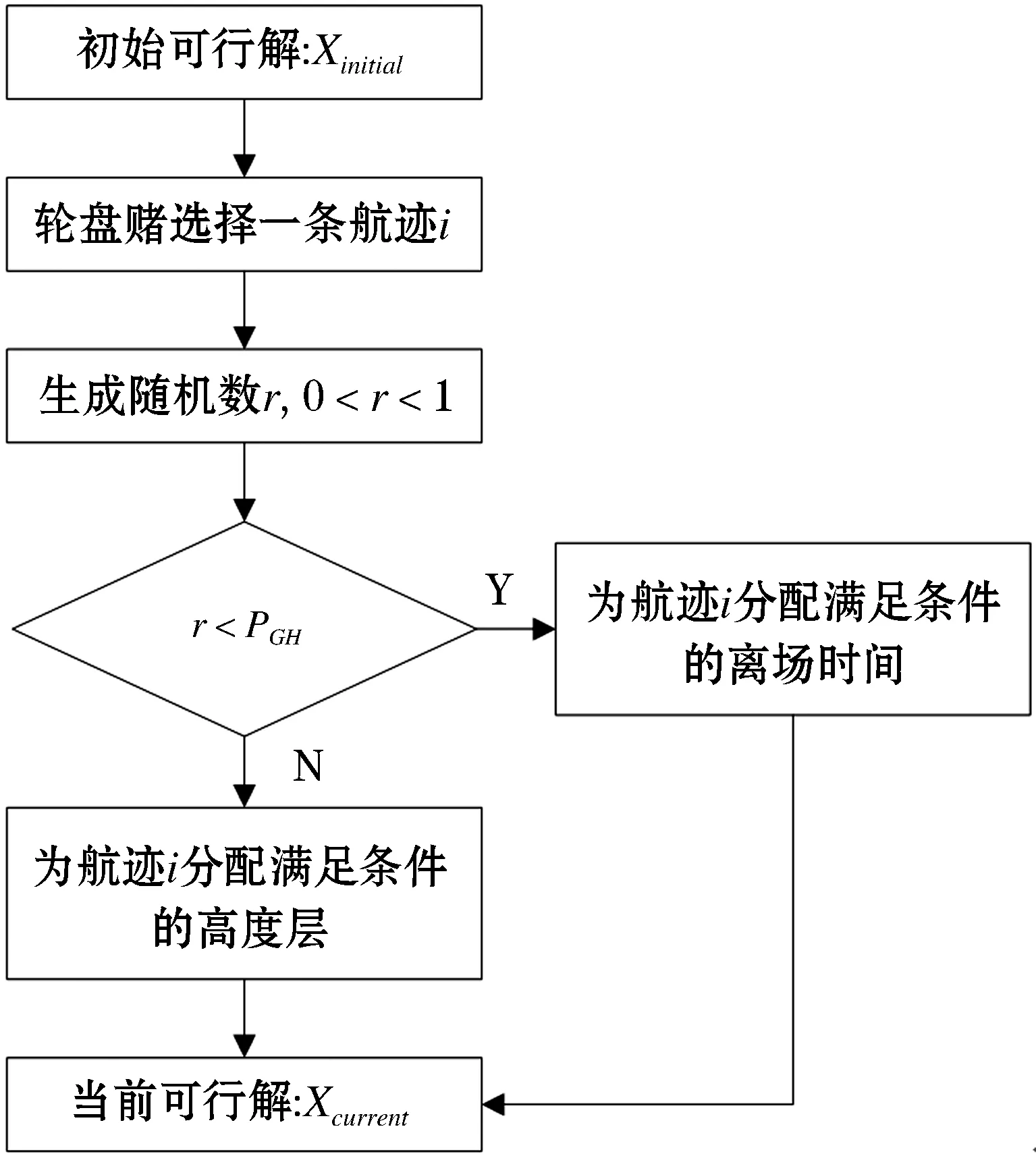

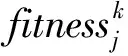
cbj=floor(εbj+(1-ε)aj)
3 仿真验证
3.1 小规模算例

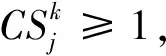




3.2 大规模算例


4 结 语

