基于Bayesian MCMC方法的美式障碍期权模拟定价
陈敦勇, 郭 洁, 孙玉东
(1.贵州民族大学 数据科学与信息工程学院, 贵阳 550025; 2.贵州民族大学 商学院, 贵阳 550025)
随着金融市场的日益繁荣, 大量金融工程师及其他金融爱好者对期权定价的相关内容做了大量研究.文献[1]在次分数布朗运动的前提下, 考虑了连续支付红利的问题, 并且利用It积分和微分方程给出了期权的定价公式.文献[2-3]介绍了基于马尔科夫链蒙特卡洛(Markov Chain Monte Carlo, MCMC)算法和使用蒙特卡洛(Monte Carlo, MC)方法的三叉树模型对美式期权定价, 通过Gibbs抽样给出较合理的定价方法.文献[4,9]介绍了在跳跃模型下使用(Least Square Monte Carlo, LSM)方法对美式障碍期权定价问题, 基于LONGSTAFF等人所提出的最小二乘方法, 提出加权最小二乘、偏最小二乘方法对期权定价进行研究.文献[5,16]对经典布莱克—斯科尔斯(Black-Scholes, B-S)模型给出了障碍期权的定价公式并且分析了估计误差的问题, 并且还设计了一种针对该模型的神经网络算法, 给出了期权价格的数值近似.文献[6]基于开源统计软件R语言对MCMC方法做了详细的介绍, 并给出方差减少技术的使用.文献[7]利用时变二叉树模型研究了Bermuda型理财产品进行期权定价研究, 对波动率和收益率序列的历史数据建立时间序列模型, 指出该类型的理财产品选择自动再投资对投资者更有益.文献[11,13,14]介绍了蒙特卡洛方法在期权方面的应用,并且在文献[19]中介绍了利率、积分、差分格式、期权定价的诸多模型及大量关于期权方面的问题, 为期权定价研究提供了一些指引.对于期权定价, 诸多学者做了大量贡献[12-21], 这对于后面研究期权定价提供了很好的参考.
在LONGSTAFF等人所提出的最小二乘方法的基础上, 出现了加权最小二乘、广义最小二乘和广义矩估计等方法. 受其启发, 用加权最小二乘与蒙特卡洛方法相结合, 得到加权最小二乘蒙特卡洛(Weighted Least Squares Monte Carlo, WLSM)方法, 此方法在计算速度和效率方面能够得到很大的提升. 本文的创新点有:1)考虑了是否需要支付红利的问题展开讨论; 2)在蒙特卡洛方法中随机数的生成从任意随机数改成从指定Faure序列产生随机数来代替伪随机数序列; 3)分析了障碍期权中障碍值的设置; 最后对数值模拟结果作了“均值再取均值”等多方面的分析.
本文介绍标的资产价格过程和WLSM方法所涉及的相关知识. 在市场无摩擦情况下, 比较了不支付红利与需要支付红利标的资产过程的区别, 并采用数学公式表达, 给出期权价格路径的计算方法, 同时介绍了WLSM方法美式障碍期权定价原理及其算法步骤. 由于LSM方法中对期权定价存在误差过大的问题, 原因是该方法采用伪随机数产生序列, 因此针对此问题WLSM方法采用Faure序列产生随机数来代替伪随机数序列, 这样得到的随机数更加均匀,可以避免出现聚集现象, 且使算法的收敛速度得到一个明显的提升.
1 WLSM方法的障碍期权定价
考虑标的资产价格遵循几何布朗运动, 体现价格连续变化的过程, 不考虑标的资产价格会出现如破产、人为投机、政策调整等因素而引起的“跳跃”现象. 因此可以从标的资产过程、是否需要支付红利、随机化Faure序列等几个方面对WLSM方法在障碍期权模拟定价上进行讨论分析.
1. 1 标的资产过程
假设市场不存在套利机会且不用支付红利的情形下, 由文献[19]可得, 风险资产价格可由式(1)表示:
Pt=P0exp{(μ-0.5σ2)t+σ(Wt-W0)}.
(1)
其中:Pt为t时刻的资产价格,μ,σ分别是预期回报率和波动率, {Wt,t≥0}是标准布朗运动.然而许多风险资产往往都会要求支付红利, 一方面支付红利会降低股票价格, 同时对期权价格也造成一定的影响, 导致期权价格下降;另一方面也会增加期权持有者的收益.设红利率为q, 在时间[0,t]上支付n次红利, 则资产价格的剩余价值变成(1-0.5qt)n×Pt, 当n→∞时, 根据重要极限定理可得到(1-qt/n)n→exp(-qt), 此时实现了连续支付红利.在物理测度ρ下,r和μ是等价的, 于是在支付红利的情形下, 风险资产价格满足式(2):
Pt=P0exp{(r-q-0.5σ2)t+σ(Wt-W0)}.
(2)
可据此计算出t时刻的价格, 根据美式期权的特征, 采取向前倒推的方法得到初始时刻资产的价格.假设在ti时刻ti=t+i×Δt,i=0,1,2,…,n, 其中:(Δt=(T-t)/n), 则布朗运动满足Wi+1-Wi~N(0,Δt),i=0,1,2,…,n-1, 当i≠j时满足Wi+1-Wi与Wj+1-Wj相互独立, 抽取正态随机数ξ1、ξ2、ξ3、…、ξn其中:(ξi~N(0,Δt)), 并将其依次代入式(3)得价格的第j条路径轨迹,
(3)
同理, 重复从分布N(0,Δt)中抽取正态随机数ξ1、ξ2、ξ3、…、ξnN次, 继续代入式(3)就得到N条路径, 于是得到路径价格矩阵A, 该矩阵对后续的计算起到重要作用, 从它的最后一行倒推到第一行即为期权的初始价格.
1. 2 WLSM方法的方差减少技术
降低方差技术如对偶变量法、控制变量法、重要抽样和分层抽样等多种方法可以减少有效地方差. 本文针对WLSM方法, 介绍了低差异序列和对偶变数法, 并且对低差异序列随机化, 更进一步改善蒙特卡洛模拟的效果. 其中Faure序列是低差异序列中最常见的一种, 将采用下面方法对其进行构造.
1.2.1 Faure序列及其随机化
由文献[15]可知, 矩阵C2和C3满足:
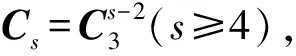
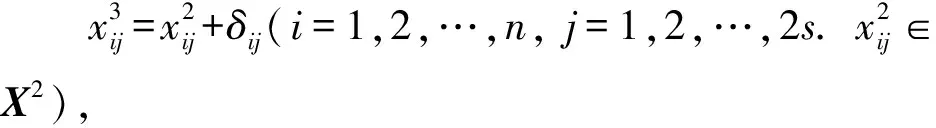
1. 3 美式障碍期权定价的(WLSM)方法模型及其算法步骤
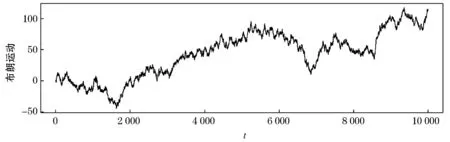
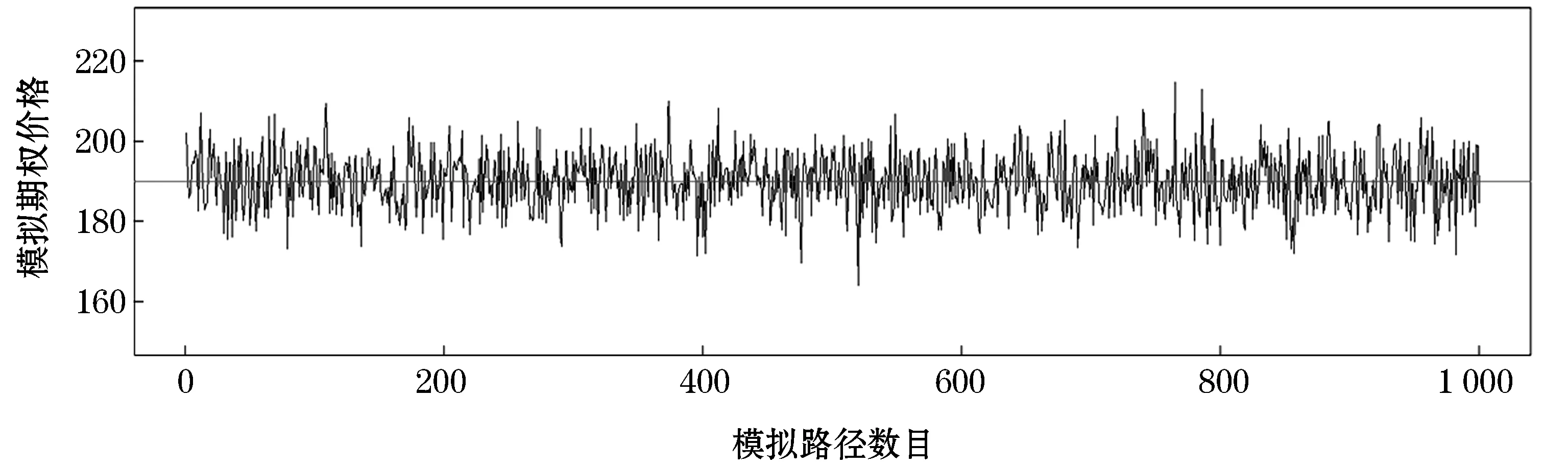
本节尝试在最小二乘方法的基础上使用加权最小二乘的方法分析了期权的定价问题. 假设一个有限的时间域[0,T], 定义Ω表示所有可能取样路径ω的集合,F为T时刻的σ-代数,L是由F的元素定义的概率测度, 在时间[0,T]内定义一个三重概率空间(Ω,F,L)和一个等价鞅测度Q[4].现在令D(ω,s),ω∈Ω,s∈(t,T)表示期权现金流的路径, 此时需要注意期权在t时刻之后执行或者在t时刻以后执行都满足最优停时策略, 即期权持有者在任何时刻执行都满足收益最大化.对于美式障碍期权, 假设执行日期是有限的0 D(ω,tj∶ti,T)|Ft)]. (4) 其中:r(ω,s)表示无风险利率,Ft为t时刻的收益. 我们知道,LSM的思想是构造一组基函数, 期权的未来收益可由这组基函数线性组合表示, 即对每一个执行的时间点, 通过WLSM来估计其条件期望. 假设在tk时刻F(ω∶tk)表示所有正交基函数的一个线性组合, 使这个过程在时间上向前一直重复迭代到第一个执行时刻, 这样就得到开始时的执行价格, 基函数可以是Jacobi行列式、Legendre多项式、Leguerre多项式和拉格朗日多项式等. 为了计算简便, 基函数使用拉盖尔多项式, 即Ln(x)=exp{-x/2}(ex/n!)(dn/dxn)(xne-x),n=1,2,…….对于式(4), 只需找一个常数ai作为系数, 该式可表示为: a2L2(x)+…+aiLi(x)+…. (5) 于是使用式(5)就能计算出ti,ti-1,…,t1时刻继续持有期权的价值, 再比较t1,i=1,2,……时刻期权价值和F(ω,ti)的大小, 若F(ω,ti)大, 那么就反向推到ti-1时刻, 直至t1时刻, 反之则执行期权, 从而确定最优停时策略, 保证持有者收益最大, 再把每条路径的期权的最大价值贴现到初始时刻, 再分别取其均值即得到初始时刻的期权价值, 总而言之就是在每个时间点上必须满足期望收益大于等于执行价格减去初始价格, 即Ek[F(w,t)]≥(K-P)+. 而对于WLSM方法与之的区别:一方面用随机化的Faure序列代替伪随机数序列;另一方面使用加权最小二乘方法代替普通最小二乘方法来估计条件期望函数的系数, 其他步骤都和LSM模型的步骤一样. 在风险中性测度[19]的前提下, 看跌期权的价格满足方程exp{-r(T-t)}×E[(K-S(t))+|S(τ),τ≤t], 在数值模拟计算期权价格时, 通过上述方程计算得到, 具体见表1. 表1 WLSM方法与其他模型定价结果对比 由于美式障碍期权具有多个执行时刻, 所以持有者在决定是否执行期权时主要参考两个方面:一方面在ti时刻执行就有最大收益(期权执行的价值);另一方面在ti以后的时刻再执行期权比在ti时刻执行得到更多的收益(继续持有期权价值大于执行价格), 这里需要注意设置的障碍值(障碍值与真实值差距小, 收益少但风险也更小即保证了收益), 上述前提是期权最高(最低)价值没有触及所设置的障碍值, 否则没有收益. 因此对期权价值变化有一个良好的判断会有效帮助期权持有者制定一个最优停时策略. 为使上述的方法模型更容易实现, 接下来通过算法的形式给出具体过程, 便于利用计算机编程. WLSM方法的算法步骤如下: Step 1 使用Faure序列和对偶变数法先模拟出期权价格路径; Step 2 利用式(3)计算模拟出的路径计算到期日的现金流; Step 3 根据计算的现金流选出实值路径; Step 4 从Step 3中挑选出的路径, 向前反推搜索到前一个执行日期; Step 5 使用加权最小二乘法估计条件期望函数; Step 6 根据Step 5估计的条件期望计算继续持有期权的价值(判断计算出的期权价格是小于等于所设置的障碍值, 否则持有者收益为零, 此时算法直接结束); Step 7 根据计算出的价值与期权内在价值相比较, 判断当前时刻是否执行期权, 做出最优停时策略; Step 8 对于每一条路径, 使用Step 7的结果调整当前折现现金流; Step 9 重复Step 3至Step 8, 一直到初始时刻, 得到每一条价格路径在初始时刻的现金流; Step 10 取每一条路径在初始时刻折现现金流的均值. 可以看到, 支付红利与不支付红利还是有所区别, 前者会给期权投资者带来额外的收益, 从某种意义上来看对保持金融衍生品持久发展有着重要意义. WLSM方法构造巧妙, 从Faure序列中抽样和使用Leguerre多项式作为基函数, 分析了障碍期权的收益问题和执行期权的最优停时策略问题, 目的是让期权持有者收益最大化. 此方法在美式障碍期权定价方面有很强的实用性和有效性. WLSM方法的算法步骤如上所述, 从中可以看到期权定价的过程, 同时在此过程中考虑到需要支付红利和障碍值的设定问题, 因为障碍水平的设置影响最后的收益, 所以在设计算法时要时刻注意. 考虑需要支付红利且设置了障碍的前提下, 设在时间区域[0,T]内, 期权到期日为T, 现在将时间分为M等份, 即0=t0 Step 4 采用倒推方式计算现金流, 重复上述步骤; 按照Step 3的方法因此向前倒推, 直至初始时刻, 取每一条路径在初始时刻折现现金流的均值即可. 本文在R平台上对所提出的WLSM模型和其他已有图树法(二叉树、三叉树)模型编写了代码, 实现数值模拟, 得到较好的参数分析结果和图形诊断. 考虑标的资产是一只股票, 在相同条件下对各模型进行随机模拟定价. 假设需要支付红利, 到期时间T为2 a, 时间间隔Δt为1/365, 也就是一年当中每天都可以交易(若有数据缺失的情况用整体数据的均值代替[20]),K=P0=1 000, 这里设σ=0.4,q=0.1,r=0.028 5, 期权障碍值设为B=700, 模拟次数设为10 000次(模拟次数越高,得到的结果更加精确). 设期权价格遵循标准布朗运动,即价格是连续变化的, 如图1 所示. 图1 期权价格的连续变化过程 根据上述的假设, 由式(3)计算该期权的一条价格路径, 此后再使用同样的方法模拟出M=1 000条路径, 并且计算出期权价格, 可以从图2中看出价格波动率很小, 说明模拟的结果较稳定. 注意, 在模拟期权路径时, 模拟的次数越高得到的结果就越精确, 图2为模拟1万个随机数等到一条路径, 然后再模拟重复1 000次得到的路径所得的结果. 图2 模拟期权价格变化情况 由图2可得期权在每一条路径初始时刻的价格, 把得到的值每间隔5个取均值(这取决于计算设备, 假如模拟出的价格路径大于100 000条, 则可以把间隔取得更大,即在上述基础上从1 000个值缩减成200个值, 再用得到的值作图,结果如图3所示, 对比图2得到的结果, 可以看出经过这样的处理之后, 一开始波动率较大, 但随着模拟的次数增多, 得到的结果就越精确, 这种方法对后续期权价格变化的稳定性分析研究提供一种新研究思路. 图3 间隔为5取均值的价格变化情况 使用本文提出的WLSM方法对美式障碍期权模拟定价与经典的B-S模型二叉树模型和三叉树模型定价进行对比, 由于支付红利对期权持有者更加有利,也能更好地推动金融市场的发展,因此在同等模型下对比了是否支付红利的区别, 假设期权真实价格为190, 各模型模拟出的具体价格见表1. 从表1中可以看出,本文所提出的WLSM模型与经典B-S模型和图树模型在同等条件下对同一个障碍期权进行模拟定价, 得到以下结论; 1)不管是哪一种模型, 在支付红利的前提下, 期权价格还是受到很大的影响, 特别是二叉树模型受到的影响最大; 2)在图树方法当中三叉树模型因为不仅考虑了期权价格上升和下降的情况, 还考虑有不变的情况, 这样更加符合实际情况, 因此三叉树模型定价比二叉树模型更为精确, 但在需要支付红利的情况下, 价格出现的波动也很大; 3)WLSM方法在模拟时会更加稳住, 模拟出的价格与真实值相比都更为接近, 即定价的精确性会更好一些; 4)由于在模拟定价中设置了障碍值, 目的就是为了得到更大杠杆, 因此障碍值的设定也会对定价造成一定的影响, 需要在设置时注意不要太大或者太小, 避免最后收益直接为0; 5)不管是那一种模型都是产生随机数的方法进行数值模拟, 从而得到的结果都是存在误差的, 本文所使用WLSM模型模拟得到的结果相对精确, 误差相对较少. 表2 各模型的均方误差 均方误差表示数据变化程度, 计算出来的值越小说明计算结果越精确. 从表2中可以看出本文所提出的WLSM方法模型的均方误差最小, 表现更好,定价更加准确, 适用性和有效性良好. 本文提出将最小二乘回归方法和蒙特卡洛模拟相结合得到WLSM方法, 该方法的改进之处是用Faure序列代替伪随机序列来产生随机数进行模拟, 可以避免出现产生的随机数集中在一起出现聚集现象, 影响模拟结果的精确性.另外,在做回归的时候考虑了权重, 使结果更精确. 本文在模拟期权定价时设定了支付红利和期权价格的障碍值, 因为红利会直接影响到期权的价格, 换句话说也是给期权持有者的一种保障, 设置期权障碍值同样如此, 一个恰当的障碍值会让期权持有者得到一个更大的杠杆, 实现收益最大化, 反之收益为零. 随着金融市场的发展, 障碍类型期权会受到更多的关注.本文给出了相应的算法步骤, 为计算机模拟提供了可能,最后在风险中性测度的前提下对期权进行模拟定价,分析了价格的波动表现, 通过使用之前已经有的模型和WLSM方法模型做对比, 结果表明本文所提出方法具有良好的有效性和可行性,并给出各个模型的均方误差.
2 美式上升敲出看跌期权(up-and-out put)的WLSM步骤
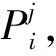


3 数值模拟定价

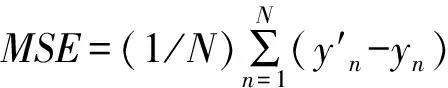

4 结 语

