曲轴装配平衡轴齿圈后弯曲变形的分析
□ 李启伟
内江金鸿曲轴有限公司 四川内江 641106
1 分析背景
随着发动机技术的不断发展,为提高发动机的平稳性,越来越多的四缸发动机装配有平衡轴机构。为了简化结构,平衡轴齿圈与曲轴采用过盈配合传递动力。
在日常生产中,在装配平衡轴齿圈之后,通常会引起曲轴弯曲变形,导致部分产品因主轴颈跳动精度超差而报废。
在曲轴研究方面,不少学者采用有限元分析方法对曲轴结构强度进行分析,但在曲轴装配变形方面研究成果仍较少。
笔者采用有限元分析方法,对曲轴装配平衡轴齿圈后的变形机理进行分析,给出弯曲变形规律,同时提出简化计算方法,为曲轴的结构设计和加工工艺设计提供参考。
2 曲轴装配平衡轴齿圈结构
某四缸发动机曲轴装配平衡轴齿圈的典型结构如图1所示。

图1 曲轴装配平衡轴齿圈结构
为保证可靠传递转矩,通常设计装配过盈量为0.1~0.25 mm,齿圈厚度为10~20 mm,装配要求齿圈加热到150~300 ℃进行压装。
3 连接面压力计算
连接面最大径向压力计算式为:
(1)
(2)
(3)
式中:Pmax为连接面最大径向压力,MPa;δmax为最大过盈量,mm;d为配合面公称直径,mm;E1为被包容件材料弹性模量,MPa;E2为包容件材料弹性模量,MPa;C1为被包容件刚性因数;C2为包容件刚性因数;d1为被包容件内孔直径,mm;d2为包容件外径,mm;μ1为被包容件材料泊松比;μ2为包容件材料泊松比。
对于曲轴装配齿圈结构,齿圈为包容件,曲轴为被包容件。计算连接面压力时,可以取齿根圆直径为d2。曲轴装配平衡轴齿圈连接面的最大径向压力通常为20 MPa~40 MPa。
4 弯曲变形机理
4.1 单个曲柄变形
先从单个曲柄再到单个曲拐逐步分析装配齿圈后曲轴的变形规律,为了便于分析,对曲轴结构进行了简化。建模及结构分析使用Creo Parametric 2.0软件。
平衡轴齿圈通常安装在曲轴的某一曲柄位置,此曲柄为圆盘状,其外圆安装齿圈。为简化分析,以曲柄两端中心直接连接圆柱体作为单个曲柄,分曲柄端面有无凸台结构两种情况进行分析。
4.1.1 无凸台时变形
在Creo软件中建立三维模型,圆盘状曲柄尺寸为φ130 mm×13 mm,两端对称分布φ50 mm×100 mm圆柱体,过渡圆角半径为3 mm。
材料为钢,在中间曲柄外圆上匀施加压力载荷30 MPa,以一个端面做位置全约束,建立静态分析,运行后应力、位移结果分别如图2、图3所示。

图2 单个曲柄无凸台应力结果

图3 单个曲柄无凸台位移结果
分析结果显示,曲柄和其两端连接圆角产生了应力和压缩位移变形,两端圆柱体远端应力和位移很微小,几乎可以忽略不计,两端圆柱体没有产生弯曲变形。
4.1.2 有凸台时变形
通常曲轴上装平衡轴齿圈的曲柄两边结构不对称,在一侧有一个凸台进行齿圈轴向限位。
在Creo软件中建立三维模型,中间曲柄尺寸为φ130 mm×13 mm,左端增加一个φ140 mm×7.5 mm凸台,两端同样对称分布φ50 mm×100 mm圆柱体,过渡圆角半径为3 mm。
材料、载荷约束采用与齿圈安装曲柄两端无凸台的相同设置。建立静态分析,运行后应力、位移结果分别如图4、图5所示。

图4 单个曲柄有凸台应力结果

图5 单个曲柄有凸台位移结果
分析结果显示,两端圆柱体没有产生弯曲变形,远端应力和位移很微小,几乎可以忽略,曲柄及连接圆角产生了较大的应力应变,曲柄和凸台不仅产生了压缩变形,还产生了向无凸台一侧的弯曲变形。
可以看出,由于左端凸台的存在,使曲柄两侧刚性不同,左侧大、右侧小,在受到安装压力时,曲柄向刚性小的一侧发生弯曲变形。
4.2 单个曲拐变形
4.2.1 变形分析
取单个曲拐进行分析。一个曲拐含两个曲柄,其中一个曲柄为圆盘状,用于安装平衡轴齿圈。曲拐的结构如图6所示,曲拐中间为偏心距45 mm的φ40 mm×22 mm连杆轴颈,两端主轴颈为φ50 mm×100 mm圆柱体,轴颈与曲柄端面过渡圆角半径为3 mm。
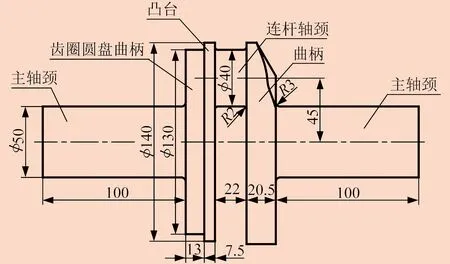
图6 曲拐结构
在Creo软件中建立三维模型,材料、载荷约束采用与齿圈安装曲柄两端无凸台的相同设置,即材料为钢,在曲柄外圆上施加压强载荷为30 MPa,以左端面做位置全约束,建立静态分析,运行后应力、位移结果分别如图7、图8所示。

图7 单个曲拐应力结果

图8 单个曲拐位移结果
整体最大位移和Y向量大位移都位于右端圆柱体端面,大小可以反映曲拐的变形程度。
分析结果显示,较大的应力应变部位产生在装齿圈的曲柄及其连接圆角附近,另一个曲柄和两端圆柱体的应力应变很微小,几乎可以忽略,两端圆柱体产生角度偏转,即整个曲拐发生了弯曲变形。
由上述分析可知,曲拐发生弯曲轴的原因为:平衡轴齿圈装配后,在连接外圆面因过盈配合产生较大的压力;由于装齿圈的曲柄两端结构强度不对称,在这一压力作用下,整个曲柄发生向强度较弱一侧的弯曲变形;由于连杆颈中心偏置,连杆颈轴线随着弯曲的曲柄发生偏转,带动与其连接的另一个曲柄和主轴颈发生同样偏转;由此,整个曲拐产生弯曲变形。
4.2.2 曲拐变形与连杆轴颈中心距关系
由上述分析可知,连杆轴颈中心偏置是造成曲拐弯曲变形的原因之一,于是分析连杆轴颈中心距的大小对曲拐弯曲变形程度的影响。
在Creo软件中建立敏感度分析,变量选择曲拐模型中连杆轴颈中心距,变量范围设置为最小30 mm、最大48 mm,出图参数选择最大位移,运行后得到最大位移与连杆轴颈中心距的关系曲线,如图9所示。
从图9中可以看出,曲拐最大位移与连杆轴颈中心距基本成直线正相关,即最大位移随连杆颈轴中心距成比例增大。
4.2.3 曲拐变形与凸台宽度关系
由上述分析可知,安装凸台的存在是造成曲拐弯曲变形的另一个主要原因,于是分析安装凸台宽度对曲拐弯曲变形大小的影响。
在Creo软件中建立敏感度分析,变量选择曲拐模型中凸台宽度,变量范围设置为最小0、最大10 mm,出图参数选择最大位移,运行后得到最大位移与凸台宽度的关系曲线,如图10所示。
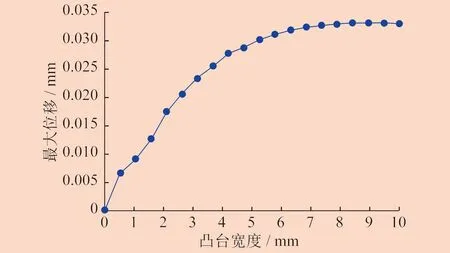
图10 最大位移与凸台宽度关系曲线
从图10中可以看出,随着凸台宽度从0增大到8 mm,最大位移从0达到最大0.35 mm,凸台宽度再增大,最大位移开始逐渐减小。
凸台宽度为0~5 mm之间时,最大位移增大较快。随着凸台宽度的继续增大,整个曲柄的强度也增大,最大位移增大变慢。当凸台宽度为8.5 mm时,最大位移达到最大值,随后开始减小。
通常受发动机结构限制,曲柄的总宽度A和齿圈安装面宽度C是确定的。设曲柄总宽度为20.5 mm,齿圈安装面宽度为13 mm。右端凸台宽度为B,在左端增加一个宽度为D的导向圆锥面,两者宽度和为7.5 mm,导向圆锥面宽度D随凸台宽度减小而增大。曲拐优化设计结构如图11所示。

图11 曲拐优化设计结构
在Creo软件中建立敏感度分析,变量选择曲拐模型中凸台宽度,变量范围设置为最小0.5 mm、最大为7.0 mm,出图参数分别选择最大位移和Y向最大位移,运行后得到最大位移、Y向最大位移与凸台宽度的关系曲线,分别如图12、图13所示。

图12 最大位移与凸台宽度关系曲线

图13 Y向最大位移与凸台宽度关系曲线
从图12、图13中可以看出,随着凸台宽度由0.5 mm增大至7.0 mm,最大位移在凸台宽度约为4 mm时达到最小值0.005 mm,Y向最大位移由-0.034mm增大到0.036 mm,在凸台宽度约为3.6 mm时达到0。Y向最大位移由负到正的变化反映了曲拐弯曲方向的变化。
由上述分析可知,当齿圈安装面一端无导向锥面时,随着另一端凸台宽度增大到某一值时,曲轴弯曲变形达到最大。当导向锥面和凸台宽度接近时,曲轴弯曲变形等于0。改变安装面的轴向位置,可以改变弯曲变形大小和方向,弯曲偏向强度较弱的一侧。可以在Creo软件中建立优化可行性研究项目,来求得最大位移最小时的凸台宽度。
5 弯曲变形计算及对精度影响
5.1 弯曲变形计算
在实际工作中,通常以两端中心孔或主轴颈中心为基准,规定中间各主轴颈的同轴度或跳动要求,在Creo软件中进行结构静态力学分析难以直接得到此数据,于是通过两端面位移数据来近似计算。
由上述分析可知,变形主要集中在安装齿圈的曲柄和其连接圆角上,其它部位变形很小,可以忽略不计。据此进行简化,取一端主轴颈轴线与曲柄端面交点为基点,曲柄向强度弱的一侧发生角度为θ的偏转,就某一具体曲轴而言,其几何结构已确定,可以认为θ是因过盈配合而产生的Pmax的函数,即压力越大,变形也越大。
曲轴变形简化结构如图14所示。设齿圈装配后曲拐右端发生以O点为基点,角度为θ的偏转,右端中心B点偏移到B′点。在Creo软件中进行静态分析,可测得右端变形位产生的移量Δy为BB′的长度。由曲柄轴向位置L0可算出偏转角θ,再由总长L即可近似求得长度为Li点处中心相对新的两端中心连线AB′的偏移量Δyi。通常情况下,Δy远小于L,忽略高阶量,可按下式计算:
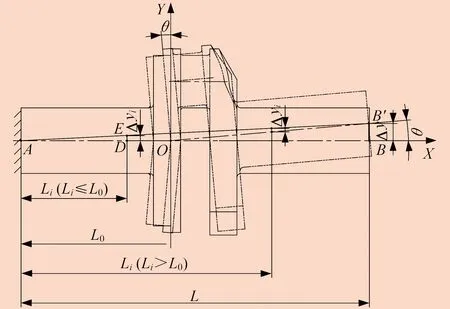
图14 曲拐变形简化结构
(4)
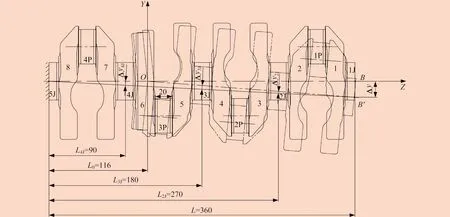
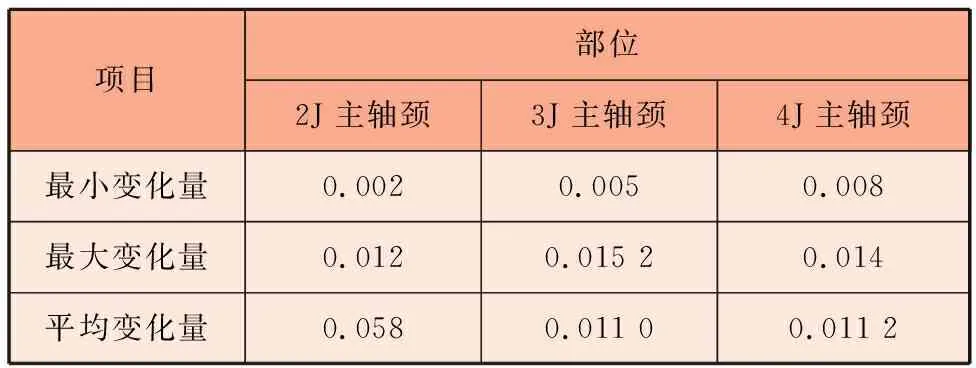
Δyi≈LiΔy/LLi (5) (6) 当以两端中心为基准测量时,某轴心点到AB′的距离Δyi反映了轴心偏移大小,2Δyi即为该点的同轴度。 从式(5)、式(6)可以看出,离曲拐两端面越远,Δyi越大,在装齿圈的曲柄处Δyi达到最大值。所以在曲柄两端的主轴颈偏移最大,即齿圈曲柄及其两端的主轴颈同轴度变化最大。 由于齿圈曲柄两端结构强度不相同,装配齿圈后曲柄发生弯曲变形,曲柄外圆会呈现一端大、一端小的锥度,进而引起齿圈内孔及外圆锥度变化、轴向齿形误差变化。曲柄外圆锥度的变化量可以在结构静态分析结果中测量得到。齿圈曲柄同轴度最终会反映在齿形径向跳动误差上。 以两端中心为基准测量时,曲轴弯曲会引起各轴颈平行度和连杆轴颈中心距的变化,如图15所示。对于在弯曲同一平面内的连杆轴颈,其中心距变化量ΔE可近似等同于该位置主轴心线变化量Δyi,即: 图15 轴颈平行度和中心距变化 ΔE≈Δyi (7) E′=E±ΔE≈E±Δyi (8) 式(8)中,根据连杆颈所在弯曲轴线的方向来确定正负,处于内凹面取负,处于凸面取正。 不考虑轴颈形状变化,忽略高阶量,长度为δL的轴颈平行度变化量δy为: δy=Δy1-Δy2 (9) 式中:Δy1、Δy2为轴颈两端中心的偏移量。 δy也可由以下方法求得,当轴颈位于齿圈圆盘左端时,为: δy=δLtanθL (10) 当轴颈位于齿圈圆盘右端时,为: δy=δLtanθR (11) θL≈arcsin(Δy/L) (12) (13) 式中:θL、θR为两边轴心线相对AB′的夹角。 2.0TM曲轴和齿圈材料均为钢,泊松比为0.3,弹性模量为2.06×105MPa。最大过盈量为0.162 mm,配合面公称直径为130 mm,曲轴内孔直径为0,齿圈外径为142.5 mm,将这些数据代入式(1),可计算出连接面最大径向压力为22.7 MPa。 图纸要求以1J、5J中心为基准测量同轴度,为方便计算,分析时将曲轴两端分别从1J、5J中心切掉。在Creo软件中对5J端面做全约束,在装齿圈的曲柄外圆面上施加22.7 MPa载荷,材料为钢,设置弹性模量为2.06×105MPa,泊松比为0.3,静态分析结果如图16所示。 图16 2.0TM曲轴静态分析结果 曲轴向2P、3P连杆颈方向弯曲,即两顶检查主轴颈跳动时2P、3P连杆轴颈方向变小。 2.0TM曲轴各主轴颈位置长度尺寸及弯曲变形计算如图17所示。由计算得2J、3J、4J主轴颈中心偏移量Δy2J约为0.003 064 mm,Δy3J约为0.006 128 mm,Δy4J约为0.006 445 mm。引起的同轴度误差φ2J为2Δy2J,即0.006 128 mm,φ3J为2Δy3J,即0.012 256 mm,φ4J为2Δy4J,即0.012 890 mm。 图17 2.0TM曲轴尺寸及弯曲变形计算 20件2.0TM曲轴装配平衡轴齿圈后主轴颈跳动变化量实测值见表1。实测值与上述理论分析计算值相符,平均变化量误差小于1.7 μm。测量值仅记录连杆颈方向上的变化量,在1P、4P连杆颈方向记为正,在2P、3P连杆颈方向记为负。 表1 2.0TM曲轴装配平衡轴齿圈后主轴颈跳动变化量 mm 曲轴装配平衡轴齿圈后发生弯曲变形的原因在于当安装齿圈的曲柄两侧结构强度不同时,曲柄在过盈配合产生的压力作用下发生向强度较弱一侧的弯曲,与曲柄中心偏置的连杆轴颈一起带动整个曲轴发生弯曲偏转。曲轴的弯曲方向具有确定性,大小主要受过盈量、装齿圈的曲柄两端结构、连杆颈中心距等因素影响。过盈量越小,弯曲变形越小。装齿圈的曲柄两侧结构强度越接近,弯曲变形越小。连杆轴颈中心距越小,弯曲变形越小。结构优化设计可减小甚至避免齿圈装配后曲轴产生弯曲变形。 曲轴装配平衡轴齿圈后变形对精度的影响会引起装齿圈的曲柄外圆锥度变化,进而引起齿圈锥度变化、轴向齿形误差等。 以两端中心作为测量基准时,曲轴弯曲变形会引起齿圈曲柄和主轴颈同轴度、平行度,以及连杆轴颈平行度、中心距测量值变化,其中,齿圈曲柄与距离最近的主轴颈的同轴度变化最大。5.2 弯曲变形对主轴颈同轴度影响
5.3 齿圈曲柄外圆锥度变化对齿圈精度影响
5.4 轴颈平行度和连杆轴颈中心距变化

6 实例分析
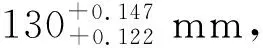
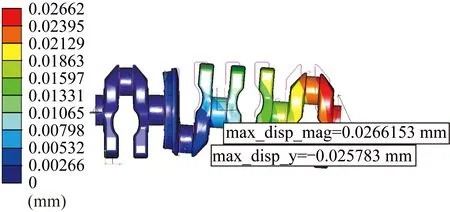
7 结束语

