共轴无人机扩展卡尔曼姿态控制研究*

□ 有德义 □ 郝永平

1.沈阳理工大学 研究生院 沈阳 110159 2.德州职业技术学院 电子与新能源技术工程系 山东德州 253034

1 研究背景

共轴双旋翼飞行器是一种上下桨同轴反向旋转且能够自主悬停的无人机,是近年来无人机研究的热点机型之一。共轴双旋翼飞行器结构与双旋翼直升飞机结构的不同之处在于没有尾旋翼平衡扭矩,具有外形尺寸小、气动效率高等优势,只需要通过上下两对螺旋桨产生的推力来保持自身平衡,飞行姿态通过舵机连接倾斜盘舵平面与下旋翼旋转平面来调整。无人机采用齿轮传动方式,将动力从电机传送到旋翼,并且上下桨叶之间存在气流扰动,加之操纵机构的复杂性和控制的非线性等原因,会导致共轴双旋翼飞行器有较明显的机械振动和噪声。

近年来,世界各国都对多传感器数据融合、滤波算法、姿态估计的问题更加关注,许多科研单位和院校对无人机姿态控制和导航做了较为深入的研究。我国对无人机姿态控制的研究起步较晚,共轴无人机姿态控制的研究还有待发展。国防科技大学、北京理工大学、沈阳理工大学等高校开展了对共轴无人机自主系统的研究,并且取得了较好的效果。吴和龙[1]在多旋翼无人机的低成本组合导航关键技术研究文章中提出基于多维状态量的高维扩展卡尔曼滤波数据融合算法,在此基础上,建立了一种基于22维状态量的高维扩展卡尔曼滤波数据融合方法,进行完整的数学模型模拟仿真试验,结果表明具有较高的准确率。沈跃等[2]在植保无人机航姿估计与分析中,采用磁力计实时校准的无人机航姿两级解算方法,这一方法考虑外界环境磁场干扰,采用无迹卡尔曼滤波器融合算法,通过四元数较好地解析出横滚角和俯仰角姿态信息。刘旭航等[3]通过卡尔曼滤波建立加速度误差模型,结合外部传感器信息,得到陀螺仪校正量,并通过计算得到的增益信息对陀螺的初始值进行校正,设计互补滤波器,滤去来自加速度计、磁强计、陀螺仪的低频噪声,从而消除传感器噪声信号对姿态估计的影响。苏黎世联邦理工大学的研究学者建立完整扩展卡尔曼滤波算法的多传感器数据融合开源框架,集成视觉传感器、全球导航卫星系统定位模块、激光雷达、超声波雷达等,达到精准的姿态定位效果[4]。无人机常见的导航估计算法有互补滤波、卡尔曼滤波、粒子滤波、神经网络滤波[5]。吴东旭[6]为了提高姿态角解算的精度,利用多传感器数据融合,分别设计互补滤波算法和卡尔曼滤波算法,并且串级比例积分微分姿态控制算法,写入嵌入式飞行控制系统中,进行飞行试验,但是在研究中并没有考虑共轴无人机自身的主要误差来源。笔者以小型折叠共轴双旋翼飞行器为研究对象,分析误差、振动的主要来源,建立姿态四元数模型,提出基于改进的扩展卡尔曼滤波的数据融合算法,并在此基础上进行载体姿态静态和动态试验对比。

2 姿态运动模型

2.1 共轴无人机结构

共轴无人机包括双旋翼、共轴机体、倾斜装置、电机、舵机、控制核心板等结构。控制核心板在共轴机体内部提供所有的控制信号。电机位于共轴机体上方,通过齿轮传动提供旋转动力,依靠两个旋翼反向转动的升力和自身重力产生合力,实现上下运动。舵机位于共轴机体的上部,采用连杆控制操控盘倾斜,进而带动下旋翼产生俯仰和横滚等姿态运动。共轴无人机简化模型如图1所示。

图1 共轴无人机简化模型

2.2 参考坐标系

在忽略地球自传和地球质心曲线运动的情况下,建立共轴无人机数学模型。为更好地确定姿态、速度、加速度和外力力矩的分量,需要引入多种坐标系。机体坐标系是固连在无人机上并随无人机运动的一种动坐标系,地面坐标系转换到机体坐标系,需要经过X轴、Y轴、Z轴旋转。定义φ为横滚角,θ为俯仰角,ψ为航向角,无人机绕X轴转动后的旋转矩阵Rx(φ)为:

(1)

无人机绕Y轴转动后的旋转矩阵Ry(θ)为:

(2)

无人机绕Z轴旋转后的旋转矩阵Rz(ψ)为:

(3)

(4)

(5)

2.3 四元数姿态解算

四元数表示三维空间的旋转信息,通过构造四元数得到变换矩阵。四元数满足:

(6)

四元数的模为:

(7)

q0=cos(α/2)

(8)

q1=lsin(α/2)

(9)

q2=msin(α/2)

(10)

q3=nsin(α/2)

(11)

式中:α为旋转矢量绕旋转轴的转角;l、m、n为旋转矢量在i、j、k虚轴上的投影。

用四元数表示姿态的优势为在任意姿态下都不会出现奇异性[7]。

(12)

用四元数来更新横滚角、俯仰角、航向角,有:

θ=arcsin[2(q2q3+q0q1)]

(13)

(14)

(15)

载体上的三轴陀螺仪可以测得共轴无人机在导航坐标系中的角速度在机体坐标系中的分量。ωx、ωy、ωz为机体坐标系下的旋转角速度,通过四元数微分方程建立的状态方程Ωb为:

(16)

采用一阶龙格库塔法求解四元数微分方程,可以得到离散时间模型q(k)为:

q(k)=q(k-1)

+Tq(k-1)[Ωb(k-1)]/2

(17)

式中:T为系统采样时间间隔;q(k-1)为k-1时刻姿态四元数。

设置初始四元数q(0),利用式(17)可以计算递推出k时刻四元数q(k)的取值,进而能够更新姿态矩阵[8]。

3 误差分析

陀螺仪测量角速度具有高动态性,但测量的是角度的导数,再对时间积分才能得到角度。陀螺仪内部运动一段时间,噪声和偏置会导致数据偏差,需要借助其它传感器进行校正。建立多维状态量,包含姿态四元数(q0,q1,q2,q3)、导航系三维速度信息(vN,vE,vD)、导航系三维位置信息(PN,PE,PD)、三维陀螺仪角增量误差(δgx,δgy,δgz)、三维加速度计增量误差(δax,δay,δaz)、三维地磁信息(mN,mE,mD)、三维地磁误差(δmx,δmy,δmz)、二维水平风速信息(vwindN,vwindE)。初始时刻四元数为:

q0=cos(ψ/2)cos(θ/2)cos(φ/2)

+sin(ψ/2)sin(θ/2)sin(φ/2)

(18)

q1=sin(ψ/2)cos(θ/2)cos(φ/2)

-cos(ψ/2)sin(θ/2)sin(φ/2)

(19)

q2=cos(ψ/2)sin(θ/2)cos(φ/2)

+sin(ψ/2)cos(θ/2)sin(φ/2)

(20)

q3=cos(ψ/2)cos(θ/2)sin(φ/2)

+sin(ψ/2)sin(θ/2)cos(φ/2)

(21)

共轴无人机的振动源主要有七个方面。第一,无刷电机通过齿轮传动装置带动上下旋翼,构成一个由电机运转、齿轮啮合等组成的机械扭转系统,进而产生机械振动。第二,上下旋翼在转动时会产生周期的空气动力,通过桨毂和旋翼轴向机体传动。其中,旋翼振动是主要振源,原因是机械不均衡和周期的空气动力相互作用。第三,微机电系统传感器安装,以及机体坐标系不对称和标度带来的误差。第四,初始条件校准时,参数和当前姿态角误差。第五,四元数计算误差、滤波算法误差等。第六,微机电系统陀螺仪因自身设计缺陷而由高动态特性产生的漂移误差等。第七,机体运动和姿态估计延时产生的动态误差。

为减小机体振动对微机电系统传感器的影响,应用补偿算法,并且在姿态解算中进行惯性测量单元传感器权重调整,同时还应该避开结构的自振频率与转子所引起的激振力频率。

4 卡尔曼滤波姿态估计

利用线性卡尔曼滤波对非线性系统的状态进行估计,采用泰勒展开式,使非线性系统在局部线性化,这样高斯分布的参数在线性变换后依然保持高斯分布,就可以使用标准卡尔曼滤波器的卡尔曼滤波结构。在非线性不强烈的情况下,扩展卡尔曼滤波器可以有效过滤掉非线性。在非线性较强烈的情况下,滤波效果会降低。建立状态方程为:

x(k)=f(x(k-1),k-1)+w(k-1)

(22)

z(k)=h(x(k),k)+v(k)

(23)

式中:x(k)为k时刻系统状态矩阵;z(k)为k时刻系统观测矩阵;f(x(k-1),k-1)、h(x(k),k)分别为非线性离散系统k-1时刻预测状态矢量函数和k时刻测量状态函数;w(k-1)为k-1时刻系统状态噪声矩阵;v(k)为k时刻测量噪声矩阵。

此处假设系统的状态量x(k)为:

x(k)=

(q0(k)q1(k)q2(k)q3(k)bwx(k)bwy(k)bwz(k))

(24)

x(k)中包括姿态四元数和三个转动轴陀螺仪随机漂移量。

初始化状态,假设初值滤波器为:

(25)

(26)

进行扩展卡尔曼滤波,时间预测更新估计为:

(27)

(28)

测量更新为:

(29)

(30)

式中:Hk是k时刻测量雅可比矩阵;Rk为k时刻观测噪声协方差矩阵。

计算k时刻卡尔曼增益Kk为:

(31)

(32)

Pk|k=(I-KkHk)Pk∣k-1

(33)

(34)

更新误差协方差时,测量更新方程利用观测变量校正状态估计和协方差估计,Fk为:

(35)

根据状态噪声和观测噪声的统计特性,只有系统的状态方程和观测方程都接近线性,扩展卡尔曼滤波才可以更接近真实值。

5 测试平台

共轴无人机飞行测试平台如图2所示,其中包含对共轴无人机升力、振动、旋翼转速等的测试。共轴无人机垂直飞行过程中,主要受到来自桨叶旋转时产生的空气动力和自身重力的影响[9]。支撑结构作为测试平台中最主要的构造部分,用于稳固机身,桨叶产生的气动力及机身受到的气动力都会通过机身结构间接或直接施加在支撑结构上。机身、传感器,以及其它构件的重力,也都会直接施加在支撑结构上[10]。共轴无人机在测试过程中,由机械结构产生的振动力同样会施加在支撑结构上[11]。测试平台通过姿态测量传感器进行静态实时稳定的姿态数据采集和测量,通过实时测量的横滚角、俯仰角、航向角信息,来分析主要误差来源。

图2 共轴无人机测试平台

支撑结构作为承受共轴无人机空气动力及自身重力的主体部件,在受力方面比较复杂。共轴无人机不仅产生维持飞行的气动升力,而且产生在发生横滚、俯仰、航向运动时的力矩。由此,共轴无人机施加在支撑结构上的力主要可以分为升力,以及横滚运动力、俯仰运动力、航向运动力。测试平台使用的测试设备包括扭矩传感器、拉力传感器、数据采集等[12-13]。

6 测试数据分析

6.1 静态姿态角

姿态角包括横滚角、俯仰角、航向角。忽略共轴无人机下方固连在万向轴上,同时忽略转台绳索约束对姿态角的影响,共轴无人机处于准静态,即输入油门量为50%时,姿态角随时间变化曲线如图3所示。测试选用扩展卡尔曼滤波和Mahony互补滤波进行对比。共轴无人机处于准静态时,采用扩展卡尔曼滤波,姿态角变化小于0.5°,而采用Mahony互补滤波,姿态角的变化接近1°。可以看出,扩展卡尔曼滤波能够很好地减弱共轴无人机的机体振动。分析100 s内采样1 000次姿态角信息,显示采用扩展卡尔曼滤波对横滚角、俯仰角、航向角都有较明显的改善作用,为前期机械结构减振滤波设计和控制算法优化提供了参考。

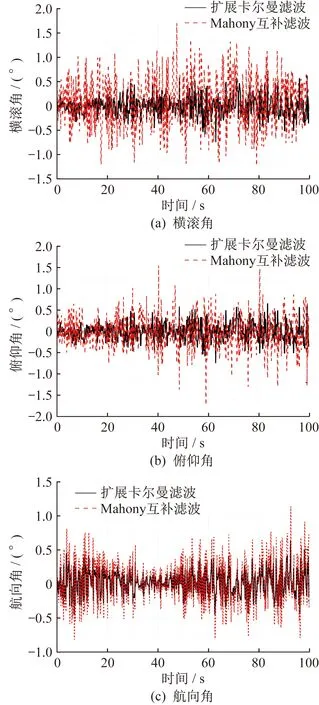
图3 姿态角随时间变化曲线

6.2 飞行姿态角

共轴无人机飞行姿态角测试处于相对封闭的校园无风环境中,如图4所示。姿态角期望值和实际值变化曲线如图5所示,二维飞行日志导出轨迹如图6所示,实际飞行路径如图7所示。

图4 飞行姿态角测试环境

图5 姿态角期望值和实际值变化曲线

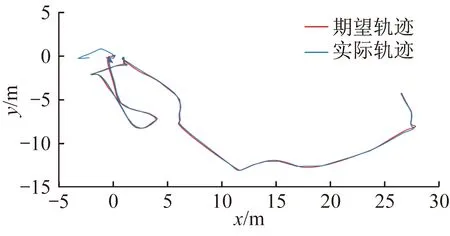
图6 二维飞行轨迹

图7 实际飞行路径

对于采集的共轴无人机振动数据,利用软件进行数据分析,具体包括60 s内的900个采样点数据。各方向位置变化曲线如图8所示。实际飞行时X方向期望值与实际值误差小于0.1 m,Y方向期望值与实际值非常接近,Z方向,即高度方向期望值与实际值同样误差较小,可见共轴无人机姿态估计跟随性较好,在一定程度上解决了误差累积和随机噪声漂移等问题。

图8 各方向位置变化曲线

7 结束语

针对小型共轴双旋翼飞行器误差源和姿态测量的问题,分析了横滚、俯仰、航向姿态特性,提出四元数扩展卡尔曼滤波数据融合算法,在此基础上进行测试分析。

在静态姿态角测试中,对共轴无人机振动幅度和频率进行分析,数据表明,扩展卡尔曼滤波在姿态估计中误差小于Mahony互补滤波。飞行姿态角测试表明,扩展卡尔曼滤波跟踪效果较好,能够减小高速飞行过程中产生的机械振动噪声对姿态角的影响,提高姿态角的稳定性和控制鲁棒性,并有效提高共轴姿态和位置估计的精度。通过研究可见,扩展卡尔曼姿态控制在无人机姿态解算中具有一定的工程应用价值。