叉车门架仿真分析与拓扑优化*

□ 徐进壮 □ 汪 伟 □ 王汝佳

江苏理工学院 汽车与交通工程学院 江苏常州 213001

1 分析与优化背景

叉车在搬运中起关键作用,广泛运用在港口、机场和物流中心等场所。叉车门架是叉车中的核心结构,门架的承载能力必须达到所规定的载荷,否则将会引起重大安全事故。一些生产厂家为了保证门架的额定承载能力,在门架的尺寸参数设计上留出过大的余量,造成了材料的浪费,同时也影响相关配套设备的设计工作,不符合轻量化的设计理念。因此,在保证叉车门架安全的前提下,如何准确地设计门架的尺寸就显得格外重要。

笔者以额定载荷为3 t的叉车为例,对叉车的货叉、货叉架、内门架、外门架进行强度分析。为了提高准确性,选取额定载荷内的五个载质量等级进行分析,计算出叉车举升不同吨位货物时允许司机产生的叉举操作偏差。在ADAMS软件中对叉车进行运动学分析,计算货叉在叉举货物时的受力、门架倾斜角度、货叉在Y方向产生的位移变化。对外门架进行拓扑优化分析,以减轻外门架的质量。叉车装配如图1所示。

图1 叉车装配

2 静力学分析

叉车在使用过程中,容易局部出现裂纹或产生一些疲劳破坏,因此,在设计过程中应该优化和改进现有的门架结构,从根本上避免此类情况发生。同时要对门架结构进行全面的静力学分析,尤其是对于容易产生应力集中的部位,要合理划分网格,正确设置载荷和接触,从而进一步提高叉车门架设计的准确性。

2.1 模型搭建及材料选择

在SolidWorks软件中建立叉车门架三维模型,主要包括货叉、货叉架、内门架、外门架,如图2～图4所示。在搭建模型的过程中,舍去一些对数据分析影响不大的螺纹孔和倒角,并通过x_t格式将三维模型导入ANSYS软件,进行有限元分析计算。货叉及货叉架的材料为16Mn,弹性模量为212 GPa,泊松比为0.31,密度为7 870 kg/m3,屈服强度为345 MPa。内门架和外门架的材料为Q345,弹性模量为206 GPa,泊松比为0.30,密度为7 850 kg/m3,屈服强度为345 MPa。

图2 货叉及货叉架

图3 内门架

图4 外门架

2.2 网格划分

考虑到模型的复杂程度,网格划分最小单元主要是四面体和六面体,对圆角处、货叉上表面及其它容易出现应力奇异的地方进行局部网格细化,减少应力奇异的出现。部分学者在有限元分析的过程中不重视网格划分,或者仅仅以网格尺寸来评判网格划分是否标准,这种做法具有一定的局限性。对此,笔者在判断网格划分是否符合力学计算标准时,引入雅可比比率、长宽比、翘曲度、单元质量因子作为指标,来评判网格划分的准确度。门架中零件网格划分参数见表1。

表1 门架中零件网格划分参数

由表1可以看到,雅可比比率和长宽比的最大值出现在外门架上,分别为0.996和2.808,翘曲度的最大值为4.46×10-15,单元质量因子的最大值为0.795。根据相关文献及实际仿真经验,当雅可比比率大于0.5,长宽比及翘曲度小于5,单元质量因子大于0.5时,是能够满足网格划分要求的。因此,本次网格划分符合分析要求,可以进行下一步仿真分析试验。

2.3 约束设置

在货叉和货叉架贴合接触的地方设置粗摩擦接触,在内门架和外门架中普通连接的地方采用固定连接,在货叉表面施加载荷模拟重物,在内门架和外门架接触的地方施加载荷,模拟链条和液压杆提供的拉力和举升力。门架上有许多焊缝,一些铰接孔与肋板之间都是依靠焊接来实现连接的,所以对一些关键交界处的焊缝进行强度分析十分有必要。内门架侧壁与底板上焊点排布如图5所示,内门架侧壁与底板上焊点处变形趋势如图6所示。

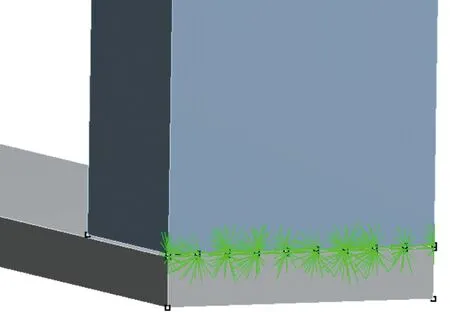
图5 内门架侧壁与底板上焊点排布

图6 内门架侧壁与底板上焊点处变形趋势

2.4 载荷施加

叉车的额定举升载荷为3 t,为了保证叉车在极限条件下依然能够正常工作,对叉车的额定载荷设置安全因数1.4。为了更加了解和掌握叉车门架的受力变化过程,分别施加2.0 t、2.6 t、2.8 t、3.0 t、4.2 t共五种载荷。载荷施加位置如图7～图9所示。

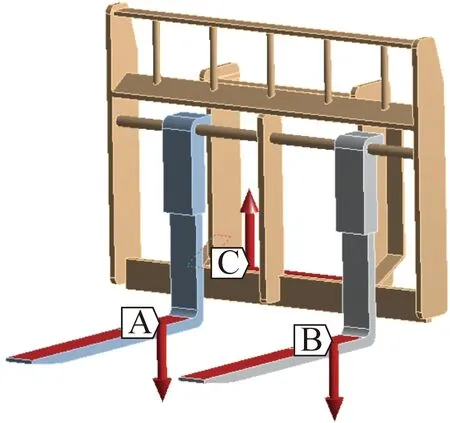
图7 货叉及货叉架载荷施加位置

图8 内门架载荷施加位置

图9 外门架载荷施加位置

2.5 叉车门框分析结果

门架中零件等效应力及变形见表2,叉车举升4.2 t货物时门架中零件受到的等效应力情况如图10～图12所示。货叉架在举升货物时,货物的重力全部作用在货叉表面,货叉以悬臂梁的形式撑起货物,货叉的根部为应力集中的区域,最大等效应力为328.31 MPa,最大变形量为22.348 mm。货叉及货叉架材料的屈服强度为345 MPa,货叉不发生断裂的最大变形量为25.32 mm。内门架和外门架的最大等效应力为344.47 MPa,最大变形量为7.212 mm,内门架和外门架材料的屈服强度为345 MPa,内门架和外门架不发生断裂的最大变形量为21.53 mm。因此,货叉、货叉架、内门架、外门架刚度均满足实际使用要求。同时内门架和外门架中一些交界处的焊缝抗压强度经检验也满足设计要求。

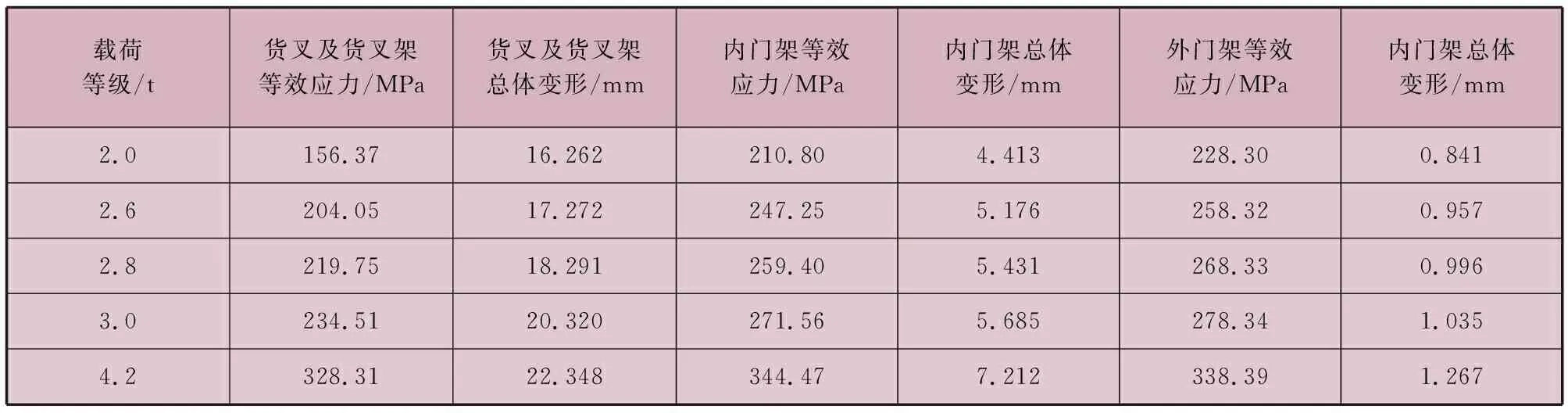
表2 门架中零件等效应力及变形

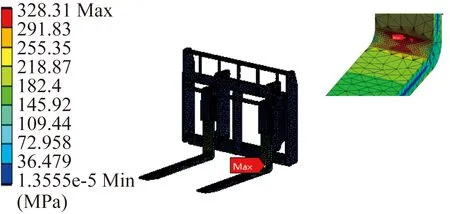
图10 货叉及货叉架等效应力情况

图11 内门架等效应力情况

图12 外门架等效应力情况

2.6 货物偏移量分析

从表2中可以发现,当载荷达到额定载荷4.2 t时,货叉及货架最大等效应力达到328 MPa,依然满足强度要求,并且有一定的冗余。同时又对单个货叉所能够承受的极限载荷进行测量,经过分析计算,得到单个货叉最大可以承载2.204 t的货物。考虑到叉车司机在举升货物过程中很难完全将两个货叉架放到货板的中心,特别对新手叉车司机而言操作比较困难,货物在举升过程中一旦出现质心偏载,将会引起货叉根部受力不均而出现裂纹,甚至导致货叉从根部直接断裂,造成难以估量的损失。因此有必要根据举升货物的载荷,计算出在不同载荷条件下允许叉车司机产生的偏载误差范围,以保证叉车司机能在举升不同货物时有足够的心理准备。以长3 000 mm、宽1 000 mm、高1 200 mm的集装箱为例,结合货叉所能够承受的极限载荷情况,计算出允许司机产生的偏差范围,见表3。在计算过程中发现,举升2.6 t及以下的货物预留给司机的偏移量较大,对叉车司机而言操作难度较小,可以忽略不计。

表3 允许叉车司机产生的偏差范围

3 运动学仿真

叉车门架举升货物是一个复杂的工作过程,货叉、货叉架、内门架、外门架在工作过程中,受力和位移是在不断变化的,这些物理量在实车测试过程中测量的难度比较大,而且在精确度上还存在较大的偏差,在参数设置上也无法及时更改。对此,笔者在ADAMS动力学分析软件中通过模拟叉车的工作过程来测量相关物理量,从而验证叉车门架工作的稳定性和可靠性,缩短试验周期,减少试验成本。

3.1 载荷及驱动添加

叉车的外门架通过固定板来实现支撑,通过液压杆控制外门架的倾斜。固定板与车身连接的一端用固定副连接,固定板与外门架连接的一端用转动副连接。液压杆与车身通过转动副连接,液压杆与外门架通过共线副实现约束。叉车在工作过程中依靠STEP函数来驱动,函数表达式为:

STEP(x,x0,h0,x1,h1)=

(1)

式中:x为时间自变量;x0为自变量初始值;x1为自变量终止值;h0为函数初始值;h1为函数终止值。

叉车车轮的驱动函数表达式为:

STEP(time,1,0,8,360d)+STEP(time,9,0,10,-360d)+STEP(time,11,0,12,360d)+STEP(time,13,0,14,0)+STEP(time,15,0,16,-360d)+STEP

(time,17,0,22,-360d)+STEP(time,23,0,24,360d)

d为车轮角速度。这一函数表示叉车在1～8 s内前进,在9～10 s内减速停车,在11～12 s内再次前进,在15～16 s内减速停车,此时叉车的货叉已经处在货物的底部,叉车然后在17～22 s内反向加速,在23～24 s内减速停车。

倾斜液压杆的驱动函数表达式为:

叉车通过倾斜的伸缩来控制门架的倾斜角度。在1～4 s内,叉车处于前进状态,货叉要向后倾斜回收,防止货叉误触。在11～12 s内,叉车已经靠近货物,需要货叉前倾,帮助叉车司机调整方向,并且也能够更方便地举升货物。

起升液压杆的函数表达式为:

STEP(time,17,0,20,0.4)+STEP(time,21,0,22,-0.4)+STEP(time,24,0,26,1.2)

这一函数表示叉车在17～20 s内升起液压杆,向上升起0.4 m,此时叉架将随内门架升起0.4 m。在21～22 s内,将内门架降低0.4 m。在24～26 s内,将内门架上升1.2 m。

货叉液压杆的函数表达式为:

STEP(time,13,0,16,-0.15)+STEP(time,17,0,20,0.3)+STEP(time,24,0,26,1.2)

这一函数表示在13～16 s内货叉下降0.15 m,用于调整货叉与货物的相对位置。在17～20 s内,货叉上升0.3 m,此时货叉已经将货物举升起来,准备退回。在24～26 s内,叉车已经退到指定位置,并将货叉上升1.2 m。

3.2 仿真过程

叉车在动态仿真的过程中主要经历三个阶段。第一个阶段是叉车的门架向后倾斜,叉车前进靠近货物。第二个阶段是叉车调整货叉的倾斜角度,将货叉放入货物的底部,并且将货物举升。第三个阶段是叉车向后退回,并将货物举升至指定高度。叉车动态仿真过程如图13～图16所示。

图13 叉车启动

图14 叉车前进

图15 叉车开始举升货物

图16 叉车举升货物

3.3 仿真分析

在ADAMS软件中,通过Measure模块可以测得受力和角度变化等信息。本次动态仿真举升的货物载荷为4.2 t,分别测量货叉工作过程中受力变化、门框上所有铰接孔位移变化,以及门架工作过程中倾斜角度变化等。

由于自身充满灵性，再加之身体条件非常优越，经过一段时间的刻苦训练后，朱易很快便成为了中国花滑队中的“红人”，而且和队友相处得非常融洽。经过陈露的亲自点播，进步神速的朱易，也被认定是代表中国参加下届冬奥会的重点培养对象。

单个货叉受力变化如图17所示。货叉在第18 s时与货物接触,受到压力,货叉所受到的压力平均为21 kN左右。由于货叉在不断起降过程中会产生失重和超重现象,因此货叉的受力也是不断变化的,在第20 s时货叉受力约为50 kN。在货叉急速下落过程中,也会出现完全失重的情况。总体而言,货叉在工作过程中受力相对稳定,与实际情况相符。

图17 货叉受力变化

叉车在举升货物的过程中,货叉与货物直接接触,容易出现刚度不足而导致货叉变形的情况,因此要在动力学软件中分析货叉在工作时的位移变形情况。货叉举升货物时在Y方向上产生的位移变化如图18所示。货叉前端由于直接接触货物,因此位移量稍大,最大位移量为22.5 mm,仍在弹性变化范围之内,不会突破材料的屈服强度。总体而言,货叉在Y方向上的位移变化较小,符合货叉的实际变形情况。

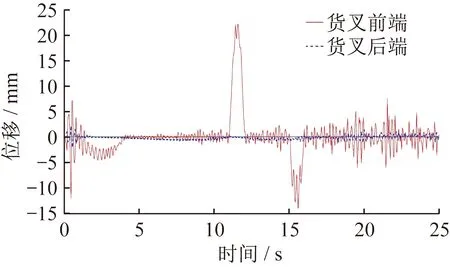
图18 货叉Y方向位移变化

叉车门架倾斜角变化如图19所示。叉车门架在2～10 s内后倾,为防止货叉与地面之间出现碰撞,最大后倾角度为8°。在11 s时叉车已经靠近货物,此时叉车门架向前倾斜,调整角度准备举升货物,最大前倾角度为6°。在17 s时货叉已经举升起货物,叉车门架保持后倾姿态,后倾角度约为2°,以防止货物在运输过程中质心不稳而滑落。

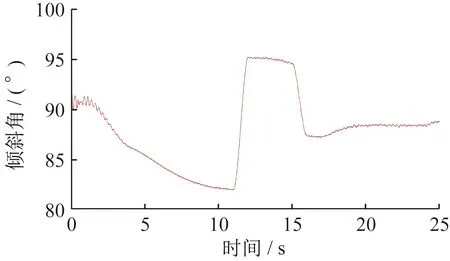
图19 叉车门架倾斜角变化

4 拓扑优化

通过静力学分析和动力学仿真,发现叉车的外门架容易产生相对较大的等效应力,同时外门架的质量较大,不符合轻量化的设计原则,因此笔者针对外门架进行拓扑优化,在满足外门架整体强度和刚度的同时,通过拓扑优化来优化外门架的局部结构,减轻叉车门架的自重。

叉车外门架的拓扑优化数学模型可以表示为:

V<<δV10<δ<1

minf(ηi)

s.t. 0<ηi<<1i=1,2,3…,N

式中:f(ηi)为外门架的质量;V和V1分别为外门架优化后和优化前的体积;δ为缩减体积百分比。

对外门架进行拓扑优化设计时,设置拓扑优化最大迭代次数为500,最小归一化密度为0.001,收敛精度为0.1%。优化之后,确定外门架的质量保留比为87%,同时外门架的强度和刚度几乎保持原有的状态。

经过拓扑优化分析,拓扑优化的目标曲线和拓扑优化的质量约束曲线分别如图20、图21所示。从图20、图21中可以发现,质量响应收敛一直向质量响应准则靠近,组合目标收敛趋势与组合目标收敛准则相差较小,满足拓扑优化要求。

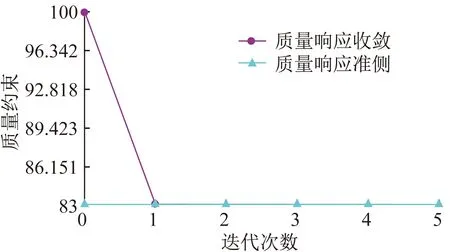
图20 拓扑优化目标曲线

图21 拓扑优化质量约束曲线

在ANSYS软件中得到拓扑优化后的模型,发现外门架顶端的加强肋板存在较大的设计余量。软件拓扑优化后外门架如图22所示。根据拓扑优化分析结果,对外门架顶端的加强肋板进行结构优化。实际拓扑优化后外门架如图23所示,质量减小9%。对拓扑优化后的外门架重新进行静力学分析,外门架的强度和刚度满足设计要求。

图22 软件拓扑优化后外门架

图23 实际拓扑优化后外门架

5 结束语

笔者对叉车门架进行仿真分析和拓扑优化,应用有限元分析软件计算出货叉在不同载荷下产生的应力和变形,同时计算出货叉能够叉举的极限载荷为4.408 t,得到叉车司机在举升4.2 t货物时允许的最大叉举误差为70.8 mm。

通过对叉车进行运动学仿真,叉车在举升4.2 t货物时货叉平均受力为21 kN,货叉在Y方向上的位移变化合理,叉车门架的最大倾斜角为前倾6°、后倾8°,使货物的质心保持在相对平稳的位置,有效防止货物滑落。

在保持叉车门架原有强度和刚度的基础上,对外门架进行拓扑优化。经过拓扑优化,外门架的整体质量减小9%,拓扑优化后的叉车门架经校核满足使用要求。