基于神经网络的非线性滤波残差估计非均匀校正算法
张科航,宋鸿飞,谭文,曹文晓,郭飞
(长春理工大学 光电工程学院,长春 130022)
红外焦平面阵列作为红外热成像的主要发展方向,因其灵敏度高、探测能力强、对恶劣气候条件适应性强[1]等特点,已广泛应用于军事、航天、民用等领域。新冠疫情以来,红外热成像系统再次凸显其重要作用,许多场所设置了免接触自动测温,迅速有效地检测出体温异常,从而快速地阻断疫情的传播,为疫情的防控做出了很大的贡献。
然而,由于非均匀性技术水平的限制,不同的焦平面阵列像元具有不同的响应速率,从而产生定模噪声,严重影响红外系统的成像质量。特别是焦平面阵列的列像素使用相同的积分读出电路,导致成像时产生列条纹噪声。此外,由于固定噪声会随着温度和时间的变化而变化,因此无法对非均匀性进行精确的校准[2]。
目前,非均匀校正算法分为两个方向:一种是基于标定的非均匀校正(calibration-based),典型的方法有两点校正法、多点校正法和挡板校正法。这种方法的优点是计算简单,校正效果明显。缺点是需要周期性地通过辐射源[3]或挡板提供均匀的场景作为校正源,在实际应用中,这种方法会周期性地造成目标的损失。
另一种方法是基于场景的非均匀校正(scene-based),典型的方法有:Scribner 提出的神经网络方法[4];Narendra 等人[5]提出的常数统计方法;Yang 等人[6]将人工神经网络移植入FP6A;牟新刚等人[7]提出了残差编解码网络;Yan 等人[8]提出了基于图像配准的方法;Qian 等人[9]提出的空间低通和时间高通算法。这种方法根据图像本身的统计特性自适应估计增益和偏差系数,容易受到场景的影响从而产生鬼影等问题。
图1 为非均匀校正前后对比图,传统的红外非均匀校正算法在稳定性与校正的质量上还存在不足,影响红外探测器的成像质量,后期的检测识别与跟踪算法的精度受到影响[10]。

图1 非均匀校正前后对比
本文提出了一种基于场景的非均匀校正算法来去除非均匀性列条纹噪声和随机噪声。非均匀性一般是一种固定的模式噪声,严重影响红外成像系统的图像质量,并在原有非均匀性的基础上随时间和温度的变化而变化。传统的残差计算忽略了非均匀性的特点,场景细节的变化会被误认为非均匀性而被过滤掉。该方法假定单列包含足够的成像信息,列元素之间的固定噪声相互独立,相互影响可以忽略,目标列元素与相邻列元素之间对场景成像存在正态分布影响,目标列元素的成像可以用相邻列元素表示。该方法利用非线性滤波滤除单列的非均匀性和随机噪声,得到单帧NUC 图像,并计算与原始图像的实际残差。然后利用前一帧的预测残差和实际残差得到当前残差。最后,根据全局运动参数控制算法自适应计算增益系数和偏置系数,以减小伪影。与其他自适应校正方法相比,该方法能在一定程度上保护图像边缘,收敛速度更快。
1 算法概念与分析
1.1 非线性滤波
红外图像相邻列具有相似的灰度分布[11-13]。假设单列包含足够的成像信息,列元素之间的固定噪声相互独立,相互影响可以忽略,目标列元素与相邻列元素之间对场景成像存在正态分布影响,目标列元素的成像可以用相邻列元素表示。假设图像有M行N列(j∈[0,N- 1 ],i∈[0,M- 1])。首先,算法需要对图像的每一列进行排序,以获得序列Seqj[i],并保持原始索引为Indexj[i]。然后用高斯核滤波,计算每列序列为Seqgauss[i],通过高斯核滤波得到第j列变换序列,如公式(1)所示:
其中,d= 3σ;k是相邻列与第j列之间的距离;Gauss(k)是高斯滤波器核。计算如下:
其中,σ为高斯标准差,可以根据经验选择最优的标准差。不同的标准差对同一幅图像的校正效果不同,算法的收敛时间也不同。影响仅存在于相邻列中,因此σ不宜太大,因为太大容易造成图像失真,而太小则滤波效果不明显。图2为同一非均匀图像在不同σ下的预测图像。

图2 不同高斯标准差σ 下的预测图像
最后,根据变换序列和原始索引恢复各列像素:
其中,Fj[Indexj[i]]为第Indexj[i]行第j列的灰度值。每列像素变换的转换公式如下:
其中,°是将Seqj转换为Seqgaussj,并根据映射恢复像素值的运算符;F(i,j)为反向映射后的像素值;u(i,j)为坐标(i,j)处的原始灰度值。通过非线性滤波操作滤除了大量的条纹非均匀性,画面纹理得到了改善,但存在部分随机噪声与随机非均匀性,需要通过采样操作减少随机非均匀性。
1.2 交叉采样
经过非线性滤波后,大部分条纹非均匀噪声被去除。然而,随机非均匀噪声仍然需要采样。交叉采样的目的是在保护原始像素细节的情况下对随机噪声进行滤波,从而得到当前帧的最终预测图像。交叉抽样的规则是:
其中,Di,j[n]是交叉采样后坐标(i,j)处的像素值;Fi,j[n]是采样前坐标(i,j)处的像素值;μ是采样参数。采样操作是为了提高算法收敛的条件,提升算法收敛的图像均匀度,对图像进行一次预滤波操作,交叉采样后得到红外图像的预测帧,将预测帧作为算法的期望帧,接下来需要自适应地通过更新每一像素点的增益与偏置系数来不断迭代,达到每一像素点的收敛,从而达到非均匀性的抑制效果。
1.3 残差估计神经网络算法
为了实现对模型的响应函数进行实时校正。传统神经网络方法使用四个邻域的均值作为预测图像,对于条纹噪声,算法效果不理想,而且传统神经网络方法图像信息丢失严重,忽略了非均匀性的特点,无法保护图像边缘[12-14]。本文兼顾温度与时间对非均匀性的影响,通过当前帧预测残差与当前实际残差得出当前残差,通过梯度下降进行增益与偏置的校正,最后通过伪影抑制参数进行场景优化。线性校正模型输出函数表示为:
其中,Xi,j为焦平面探测器的响应值;Yi,j为非均匀校正后的输出值;Gi,j为增益系数;Oi,j为偏移系数[15];ϵ为随机扰动误差,是由于不确定因素产生的细微误差,算法实际应用时为了简化算法的复杂度可忽略不计。
对于线性响应校正模型,为了实现动态校正,算法需要对增益和偏置系数分别进行动态校正和更新,本文假设经过非线性滤波处理和交叉采样的第n帧图像的像素值为Di,j(n) ,经过非均匀性校正的原始图像的输出值为Yi,j(n) :
误差函数Ei,j(n)可以简化表示为:
残差估计项可由上式得到:
当输入帧数为第一帧时,残差估计项退化为平方差损失函数,当输入帧数大于等于2 时,当前残差项为根据上一帧残差得出的当前帧预测残差与当前实际残差的加权平均,其中Ei,jn-1是前一帧的残差,Ei,jn是当前残差,Wn是实际残差的置信权值,Wn-1是预测残差的置信权值,Wn和Wn-1遵循如下规则:
R(n)为残差估计项,可由下式表示:
其中,β是温度噪声增长参数,与温度变化成正比;Tmax是最高可探测温度;Tmin是最低可探测温度,tn是焦平面阵列(FPA)温度,γ是时域噪声增长参数,随时间或帧数逐渐增加。γ是原始帧间差值:
为了使误差函数最小,本文使用随机梯度下降法更新每个像素点的增益系数和偏差系数。根据误差函数,可以得到增益系数和偏置系数的变化为:
根据随机梯度下降法进行每一像素点的迭代:
其中,λ为随机梯度下降法的步长。系数的变化对灰度值影响较大,迭代步长不宜过大。和为第n帧计算出的增益与偏置也是第n+ 1 帧输出的增益和偏移量,更新后的下一帧输出为:
在算法的实际应用中,为了减少场景的快速突变对算法造成的负面影响,本文使用了场景变化阈值Mt。当阈值Mt为1 时,算法只对图像进行滤波,学习率为0。当阈值Mt不为1 时,对图像的增益和偏差进行校正。
首先,计算相邻帧的差分图像df:
其中,df是时域上相邻两帧的差分图像;X是原始图像。接着为了更好地进行计算需要对差分图像进行二值化,可表示为:
其中,Bs为二值图像[0,1],Ts为单位像素变化阈值,用于检测当前像素点。计算当前帧的运动参数:
其中,Mo为全局运动参数。将全局运动参数Mo二值化后如下:
其中,Tg为场景移动阈值。最后,下一帧输出通过伪影滤除后的修正公式可以表示为:
其中,Mt(n)为运动判断参数,通过运动帧估计可以判断当前帧是否在运动。当帧运动判断参数为1 时场景运动,增益与偏置参数停止更新;当运动判断参数为其他则算法更新增益与偏置,这样可以大大减少场景变化可能出现的伪影,提升图像的成像质量。
2 实验及结果分析
2.1 数据采集
本实验采用IRay 光电Xcore_LT 系列测温非制冷红外运动元件采集原始视频流。图像大小为640×512,仪器温度为29.3°,距离为0.4 m,机芯组件如图3 所示。

图3 IRAY光电Xcore_LT系列测温型非制冷红外机芯组件
本实验采用OpenCV4.4 开源库中的数据结构进行数据的存储与计算,采用rtsp 协议进行红外图像的读取,基于神经网络的非线性滤波残差估计算法中高斯滤波核标准差取σ= 1.25,采样参数μ= 1,增益参数Gi,j初始化为640 列512 行的全1 矩阵,偏置参数初始化为640 列512 行的全0 矩阵,为了更好地针对固定模式的非均匀噪声,减少算法复杂度,随机扰动误差ϵ忽略不计。经过多次实践经验得出Wn取0.35,Wn-1取0.65,温度噪声增长参数β取2.4,变化阈值Ts= 15,场景移动阈值Tg= 10 922。针对不同的红外图像需调整部分参数。本文算法的编程环境为VS2015,使用C++语言编写,在16 G 内存i7-6700HQ CPU @2.60 GHz 处理器下运行。
2.2 评价标准
算法评价指标主要分为主观评价指标和客观评价指标两种[14]。
从主观视觉效果上对各算法的校正效果进行分析和评价,主要判断依据为:
(1)与校正前的图像相比,校正后图像中的条纹非均匀性是否有效抑制,并且在图像中没有产生“伪影”等降低图像质量的因素。
(2)在条纹非均匀性去除效果相似的情况下,校正图像的边缘越明显,则认为该算法的校正效果越好。校正前后图像的差异,即估计噪声中包含图像边缘信息越少,视觉效果越自然,越接近真实的边缘噪声,认为该算法的校正效果较好。
(3)经过算法的非均匀性校正,图像中的条纹非均匀性得到了一定程度的去除。从图像视觉效果来看,预处理后的图像中不存在明显的垂直条纹噪声。但是,在实际情况下,在条纹非均匀性校正前后的差值图像的每一列中,也会出现不同深浅的微弱条纹噪声。
从客观层面,本文使用粗糙度(roughness)作为评价指标,粗糙度(ρ)的定义为:
其中,ρ为图像的粗糙度;I为图像原始矩阵;h为列差分卷积项;hT为行差分卷积项;‖I‖L1表示矩阵I的L1范数。ρ值越小表示图像的列差分和行差分越小,图像的噪声越小。粗糙度与国家标准非均匀性定义相比,具有更多的应用场景,在多项研究中作为非均匀性的检测指标。
本文使用不同帧数下的粗糙度(roughness),通过校正后的图像与原始图像之间的误差图像共同判断校正效果。对于相同的红外焦平面阵列,在高非均匀性环境下采集原始非均匀图像视频,本文使用共现滤波神经网络方法(CoFNN)、常数统计方法(CS)和本文提出的算法(Our method)选取200 帧原始图像进行处理,并将处理后的结果进行对比分析。
2.3 实验分析
图4 为本文所提方法校正结果的三维图像。为了更清楚地显示图像的不均匀性,本实验放大了图像。原始图像中的不均匀性严重影响了图像质量,而修正后的图像质量得到了显著提高。从图中可以看出,所提方法滤除了大部分非均匀噪声,结果表明所提方法能有效降低非均匀性。
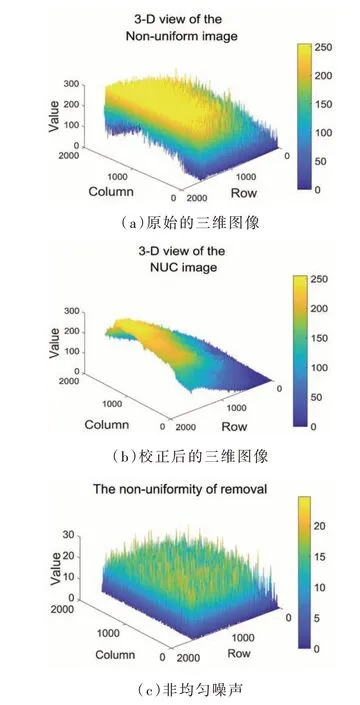
图4 非均匀校正前后去除的非均匀性
图5~7 为各算法对不同帧高非均匀性图像的校正结果。从图中标注可以看出,本文算法去除的非均匀性最直观,算法有效地降低了条纹的非均匀性,同时抑制了白噪声;对比同一时间的校正图像,在校正效果上,CoFNN 算法收敛程度较低,随机非均匀性校正效果明显但条纹非均匀性依然清晰可见;CS 算法并未达到完全收敛,结果还存在一些伪影变换。本文提出算法在收敛程度上表现最佳,本文提出的算法在非均匀性滤除的同时提升了图像的质量,相比之下传统算法只去除了部分非均匀性对条纹的非均匀性没有明显的影响。

图5 第10 帧时各算法的校正结果

图6 第100 帧时各算法的校正结果

图7 第200 帧时各算法的校正结果
图8~10 为各算法校正结果与原图像之间的误差图像(灰度图像)。从主观上来讲,图中像素点亮度越高则表示差值越高,代表滤除的非均匀性效果的强弱,从上图可以看出本文算法滤除的非均匀性显著,相比于其他基于场景的非均匀校正算法存在明显的优势。从空间上看,与COFNN 算法和CS 算法相比,结果表明,所提算法无论在第10 帧还是第200 帧都具有明显的优势,对噪声的滤波效果更为明显。从时间上看,在收敛程度相同的情况下,收敛帧数要小于其他两种算法。

图8 第10 帧时各算法校正结果差分图像

图9 第100 帧时各算法校正结果差分图像

图10 第200 帧时各算法校正结果差分图像
图11显示了在聚焦状态稳定下一段时间后移动杯子的每个算法的输出。在图11(a)中,CoFNN 方法没有及时更新参数进行场景的快速变换,使用了在杯子和瓶子之间移动之前的校正参数,导致输出错误,即出现鬼影。图11(b)中的CS 方法需要多帧收敛,快速移动杯子后会产生明显的鬼影。从图11(c)可以看出,本文提出的方法不产生鬼影,证明本文提出的方法可以有效地抑制鬼影。

图11 不同算法在场景变化下的校正结果
如表1 所示,在第10 帧,本文算法的粗糙度数据显示出优势,第100 帧和第200 帧的粗糙度修正数据高于CoFNN 算法和CS 算法,从客观的角度证明了算法相比于传统的基于场景的非均匀校正算法,具有更好的非均匀性滤除效果。CoFNN 算法在10 帧时,将非均匀性降低了47.6%,CS 算法在第10 帧时将非均匀性降低了21.4%,本文提出的算法在第10 帧时将非均匀性降低了52.3%,而在第200 帧结束时,CoFNN 算法滤除了55.5%的非均匀性,CS 算法滤除了24.6%的非均匀性,本文提出的算法滤除了61.3%的非均匀性,非均匀滤除效果明显;针对PSNR 来讲,如图12 所示,本文采集40 ℃的面源均匀黑体热辐射场进行实验。实验得出原始图像相比于理想图像的PSNR 为35.97,CoFNN 算法校正后的PSNR 为38.3,相比原始图像提高了6.7%,CS 算法校正后的结果为36.5,相比原始图像提高了1.9%,本文提出的图像PSNR 为40.7,相比于原始图像提高了13.4%,从PSNR 来看,本文提出的算法校正后的结果最接近理想图像。

表1 每个算法结果的粗糙度(ρ ) 与噪声等效温差(PSNR)

图12 均匀黑体辐射源测试
图13是每种方法校正后的200 帧图像的粗糙度曲线。从图中可以看出,原始图像的粗糙度在0.2 左右波动,而校正后的图像在经过一些帧后趋于收敛,从图中曲线可以看出,本文算法的收敛效果优于CS 和CoFNN,证明本文方法在非均匀性校正程度上具有理想的效果。

图13 不同算法粗糙度变化曲线
综上所述,本文提出的方法兼顾了噪声的去除和图像细节的保护,对非均匀性和随机噪声具有较好的抑制效果,同时也具有较好的抑制鬼影的能力,从主客观两方面都证明了本文提出的算法在实际应用中具有较理想的校正效果。
3 结论
为了解决红外焦平面阵列红外图像的非均匀性问题,本文提出了一种基于场景的非均匀校正方法。该方法假定单列包含足够的成像信息,列元素之间的固定噪声相互独立,相互影响可以忽略,目标列元素与相邻列元素之间对场景成像存在正态分布影响,目标列元素的成像可以用相邻列元素表示。该方法采用非线性滤波方法滤除单柱图像的非均匀性和随机噪声,并与原始图像计算实际残差。然后利用前一帧的预测残差和实际残差得到当前残差。最后,根据全局运动参数控制算法自适应计算增益系数和偏置系数,以减少伪影。结果表明,与其他校正方法相比,该方法能有效抑制鬼影,在收敛性、图像质量、校正效果和细节保护等方面具有优势,对条纹非均匀性和随机噪声也有明显的限制作用。

