调制比对低频时码信号传输性能的影响分析

林 笛，杨朝中，李实锋

（1.中国科学院国家授时中心，陕西 西安 710600；2.中国科学院大学，北京 100049）

低频时码授时技术是国际电信联盟（ITU）推荐的民用授时方式，因低频时码信号接收简单、覆盖范围广、传播损耗小，已经被广泛应用[1-3]。

随着低频时码授时技术的日益发展和需求的日益提升，需要提升BPC 的传输性能以覆盖更广的范围。研究的方向主要有改变调制比、调整码元进制、附加扩频调制等，该文提出了一种基于调制比的改善方法，可以在不改变信号调制方式和发射功率的前提下提升低频时码的传输性能，进而扩大覆盖范围，为将来改进低频时码信号体制打下基础。

1 BPC信号体制现状

目前世界上的主要国家和地区都建立了自己的低频时码授时系统，如美国的WWVB、德国的DCF77、英国的MSF、日本的JJY40/60 和中国的BPC。信号体制各不相同，BPC 的码元为四进制，效率较高；WWVB 及其他低频时码信号则为二进制，抗噪声性能较强。在调制比方面，WWVB 的调制比约为7∶1，德国的DCF77 为15∶1，我国的BPC 调制比则为10∶1[4]。

我国的BPC 低频时码授时系统载频为68.5 kHz，带宽为±1 kHz，码速率为1 bit/s，采用的调制方式为脉冲负极性键控，即在每秒的开始时刻（第0 秒、第20 秒、第40 秒除外），载波幅度下降为原幅度的10%，脉冲下降沿的起点代表北京时间的整秒时刻。不同的脉冲宽度代表着不同的时码信息，每分钟可向外发播3 帧时码信息，即每20 s 向外发播一帧，不同的码元组合代表着不同的时间信息，低频时码可以向外发播年、月、日、时、分、秒和校验位信息。BPC 信号采用了码位复用技术,理想情况下可以在20 s 内接收一帧低频时码，进而解码出时间信息。当脉冲宽度为100 ms 时，反向脉冲为900 ms，代表四进制信号的“0”；当脉冲宽度为200 ms 时，代表四进制信号的“1”；当脉冲宽度为300 ms 时，代表四进制信号的“2”；当脉冲宽度为400 ms 时，代表四进制信号的“3”。为分析方便，该文以100 ms 为单位进行分析，如图1 所示[5-8]。

图1 BPC信号示意图

如图1 所示，BPC 信号每个码元有四个可能的值，要正确检测BPC 信号的每个码元，必须检测上图四个时间间隔的电平状态。因此，接收出错误码元符号的概率等于四个时间间隔中任意一个时间间隔出错的概率。如果前100 ms 信息的错误概率为p，则下面三个时间间隔出错的概率均为p。考虑到两个及以上时间间隔检测错误的概率，设接收机接收一个BPC 信号码元时总的错误概率为pe，则:

考虑到低频时码本身的信号特性和应用场景，有理由假设p很小，即p4≪p3≪p2≪p。因此，可以近似地把单个码元的错误概率pe计为4p，即单个码元的错误率为前100 ms 信息错误概率的四倍。

2 调制比性能分析

当信号在接收机端被接收时，假设低频时码信号为低电平时幅值为pe，信号为高电平时幅值为x1，设调制比为c，即：

将调制比以dB 表示，则为:

式中，X=20 lg(x0-x1) 。低频时码的两个不同的电平在噪声环境中传播情况如图2 所示。

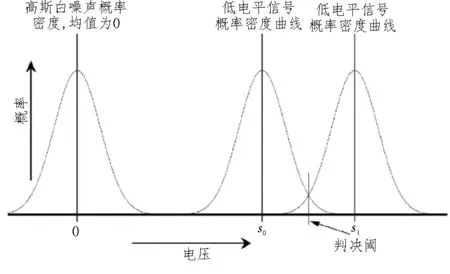
图2 低频时码电平概率密度曲线

在低频时码接收机中，信号的能量在每个码元的持续时间内积分，接收到的噪声也在相同的时间被积分。设噪声的能量为n，单位时间内低频时码码元的能量为s，则单位时间内接收到的信号能量为s+n。由于低频时码信号可能存在两个可能的电平值，所以当接收机接收到低电平时设单位时间内接收到的信号能量为s0+n，当接收机接收到高电平时设单位时间内接收到的信号能量为s1+n。接收机使用判决门限电平来判断接收到的符号，当s0+n大于门限电平时，原本的低电平信号会被错误地接收为高电平，同样的，若s1+n小于门限电平时，原本的高电平信号会被错误地接收为低电平[9]。

此时将高电平和低电平的能量差值设为y，即：

将式（4）代入式（5）可以得到：

现在可以得到在低电平幅度s0不变的情况下s1是如何依赖调制比c的，即：

此时假设Xb为无穷大，即调制比趋于无穷大的极限情况。衰减如式（8）：

此时可发现，式（8）中的结果只依赖调制比X。即当低频时码信号调制比增加时，在相同的发射功率下，接收机的解调门限会相应降低，不同调制比相比于调制比为无穷大时的信号传输损耗如图3所示。

图3 不同调制比的BPC信号功率衰减

3 信号覆盖范围分析

低频时码信号是一种长波信号，在昼间以地波传播为主[10-11]。如前文所述，低频时码调制比的增加可有效降低接收机的解调门限，进而扩大信号覆盖半径。地波传播理论是解算低频时码覆盖范围的基础。求解地波场强，就是求解符合地面边界条件的麦克斯韦方程组。在工程上通常使用米林顿方法计算分段均匀光滑地面的地波场强[12]。

3.1 米林顿方法

引入地波衰减函数Wg，它是大地电导率、相对介电常数和地波频率的函数[13-14]。米林顿方法中，由衰减函数可以给出低频时码信号接受点的电场强度E，即：

式中，P为辐射功率，d为地面大圆线传播距离，A为地波衰减因子，定义为：

在计算地波衰减函数时，对于近距离传播，近似认为地面为平面；对于远距离传播，近似地面为球面。下面就米林顿方法计算电场强度的算法进行讨论。

3.2 近距离地波衰减函数的计算

当收发点距离不大时，可以将地面等效为光滑均匀地面。设此时的地波衰减函数为W，则：

3.3 分段均匀路径的地波衰减函数计算

对于非单一介质传播路径，均匀光滑路径的衰减函数算法则不再适用，但是可以将这种混合路径划分为若干段光滑均匀的路径，每段路径按照光滑均匀路径衰减函数的算法计算出各自的衰减量，然后按特定的规则累加得到混合路径的衰减函数。

设混合路径可以划分为n段，各段的长度分别用L1，L2，L3，…，Ln表示，各段的大地电导率分别用σ1，σ2，σ3，…，σn表示。则混合路径下的二次时延（ASF+SF）由下式给出：

其中，P为发射台的发射功率，E正和E反分别是发射功率为1 kW 时正向计算和反向计算时的场强。

在电导率为σ1的均匀路径上，传播距离从增加到时场强减少的分贝数如式（18）：

3.4 覆盖范围仿真计算

因为我国低频时码信号发播台位于河南商丘，且覆盖范围大多为陆地，所以按照远距离单一传播路径来计算其覆盖范围。中国大陆的平均电导率为2×10-3Sm，介电常数为15。将相关参数代入式（18）中可以得到表1[15-16]。

表1 调制比改进前后不同场强覆盖范围

表1 通过理论计算得到了调制比增加前后不同场强的覆盖范围，可以发现低频时码信号调制比的提升可以有效提升其覆盖范围[17]。

4 结束语

该文描述了低频时码发展现状，分析了我国BPC 低频时码信号的信号体制，并结合我国的低频时码信号体制分析了低频时码的误码率和信号衰减情况。通过理论推导证明了调制比对低频时码传输性能的影响。最后，通过米林顿方法，分析了提升低频时码信号的调制比对其覆盖半径的影响。

通过分析可知，提升低频时码信号的调制比对提高其覆盖半径有一定贡献，随着传播距离的增加，信号场强逐渐减小，但是在相同场强情况下，调制比的增加有利于信号解调成功率的提升。该结论可为以后BPC 低频时码信号体制的改进提供理论基础。