插电式混合动力汽车加速度预测及能量管理

王超，薛斌强

（青岛大学自动化学院，山东青岛 266071）

为缓解能源和环境压力，新能源汽车成为汽车产业的重点方向[1]。PHEV 具有排放量低、行驶里程长等优点，是新能源汽车的研究热点[2]。其中，PHEV的能量管理策略是决定混合动力汽车燃油经济性的关键技术[3-4]，其主要有基于规则的能量管理策略[5]和基于优化的能量管理策略[6-7]两类。基于规则的控制策略简单实用、控制成本低，在实际车辆中应用广泛，但是此策略的控制规则通常通过工程经验制定，优化效果和适应性较差[8]。基于优化的能量管理策略包括瞬时优化和全局优化。以等效油耗最小策略为代表的瞬时优化能量管理策略执行效率高，但是无法保障全局最优，且等效因子的最优取值问题难以确定[9]；基于全局优化的能量管理策略可以实现理论上的最优控制，但全局优化算法程序复杂、运算量大，难以实现实时控制[10]。除此之外，电池精确建模也是混合动力汽车能量管理中的关键部分，为了将电池的电流和电压与动力系统其余部件的功率相关联，通常使用电池等效电路模型[11]。基于充放电试验数据建立Rint 等效电路模型[12]简单直观，计算量小，但精度较低。文献[13-14]采用一阶等效电路建立电池模型，相比于Rint 等效电路模型考虑了电压的动态特性，精度更高且模型参数容易辨识。

针对上述问题，设计一种基于随机模型预测控制的PHEV 能量管理策略。选择加速度为预测量，采用马尔可夫链模型进行预测，根据车辆纵向动力学模型和预测的加速度信息求解预测时域内的需求转矩。根据全局优化结果制定理论电池荷电状态（State Of Charge，SOC）参考曲线，添加关于SOC 的代价函数，防止SOC 快速下降。选择DP 求解预测时域内的最优转矩分配，确定SOC 可达区域并在此区域内离散SOC，减少计算量。

1 动力系统模型

1.1 整车纵向动力学模型

针对具有并联结构的PHEV 展开研究，分析其动力学模型。PHEV 有发动机和电机两个动力源，也有连接外部电网的接口。发动机和电机通过齿轮等结构将转矩耦合后输入到主减速器再传递到车轮，提供车辆行驶过程中的总需求转矩。其系统结构图如图1 所示。

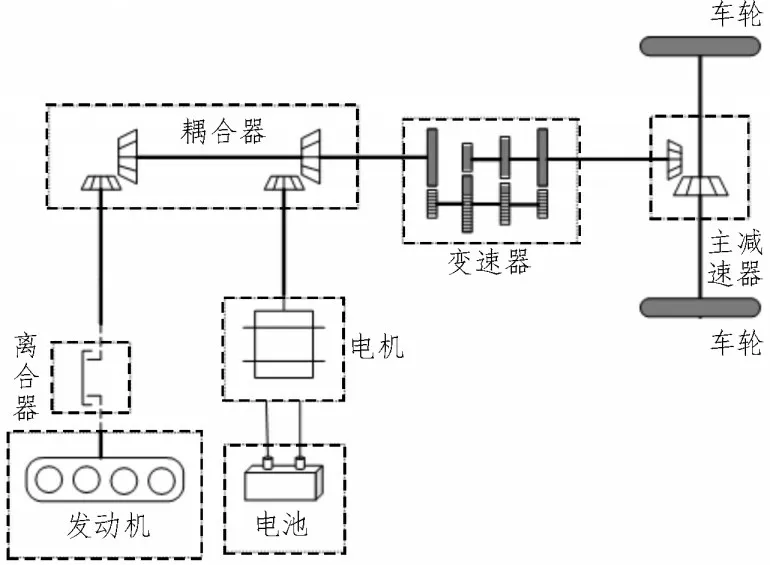
图1 插电式并联混合动力汽车结构简图

通过对整车能量分析，PHEV 的纵向动力学模型为：

其 中Tr为需求转矩；ηT为传动效率；i0为主减速器速比；rw为车轮半径；Cd为空气阻力系数；Af为迎风面积；v为车速；m为整车质量；g为重力加速度；f为滚动阻力系数；θ为坡度角；δ为旋转质量换算系数。

1.2 动力电池模型

电池作为电化学能量储存系统是混合动力汽车的关键部件，因此电池建模是影响混合动力汽车能量管理的重要因素。混合动力汽车中动力电池为多个单体电池串联或多个模组并联组成的电池组。电池组的一阶RC 等效电路[15]如图2 所示。串联电阻R0为欧姆内阻，表示由于电线和电极间的实际电阻以及降低终端可用净功率的耗散现象产生的欧姆损耗；电阻Rp和电容Cp分别为极化内阻和极化电容，两者组成的RC 回路用于模拟电池的动态响应。

图2 一阶RC等效电路模型

通过基尔霍夫定律和欧姆定律，可得：

式中，VP为RC回路上的电压；VL为负载电压；Voc为开路电压；Δt为采样时间；I为电池输出电流。为了提高论文可读性，在后续的公式中用A表示exp(-Δt/CpRp)。

根据公式（2），电流的显式表达式为：

式中，Tm为电机转矩；ωm为电机转速；ηm为电机效率。

假设所有电池单体的特性相同，整个组件的参数可由电池单体的参数进行计算：

Ns是模组中串联的单体电池数；Np是并联的模组数；Voc,cell、R0,cell、Rp,cell和Cp,cell分别为组成电池组的单体电池的开路电压、欧姆内阻和RC回路上的电阻和电容。

通过恒流放电测试和混合脉冲功率特性（HPPC）测试，分析电池的电压响应并记录数据。通过最小二乘法对记录的数据进行拟合，获得Voc,cell，R0,cell，Rp,cell和Cp,cell与SOC 之间的非线性关系：

式（5）-（6）中，bi、ci、di、ei和f1为多项式拟合系数。

结合式（3）-（6），电池组的荷电状态SOC 表示为：

式中，SOC0为电池组的SOC 初始值；Qb为电池组容量。

2 随机模型预测控制

基于模型预测控制的能量管理策略是基于预测的未来工况将全局最优问题转化为预测时域内的局部最优问题，通过滚动优化不断更新预测时域内的优化问题，使优化结果接近全局最优。

2.1 马尔可夫加速度预测模型

为了实现PHEV 的最优转矩分配，需要准确地预测出车辆未来的行驶状态。由于车辆未来状态仅取决于当前状态，具有较强的随机性和无后效性[16]，因此，采用马尔科夫链模型对加速度进行预测，其中马尔科夫链建立步骤如下：

采用近邻法将加速度a离散为p个状态，Pi,j表示k时刻加速度为ai条件下，k+1 时刻加速度为aj的转移概率，Pi,j为概率转移矩阵的第i行第j列元素，可通过最大似然估计法计算，Mi,j为加速度从ai转移到aj的次数，Mi为加速度从ai转移的次数。

2.2 随机模型预测控制的建立及求解

通过上述的马尔可夫模型以及当前的车辆行驶状态能够预测出车辆在预测时域内的加速度信息，并结合车辆纵向动力学模型计算得到预测时域内的需求转矩。这样预测时域内的能量管理问题可以描述为以动力电池荷电状态SOC 为状态变量，驱动电机转矩Tm为控制变量，燃油消耗量最小为优化目标的模型预测控制优化问题。

优化过程中，系统当前时刻的状态量由前一时刻的状态量和控制量确定，在每一次决策之后都会引起状态转移，状态转移方程为：

把预测时域内PHEV 的油耗作为优化目标，则在k时刻给出混合动力汽车能量管理系统的预测控制性能指标：

式中，Jk为预测时域k～k+p内总的燃油消耗量；L为预测时域内每个时刻的瞬时油耗；Te为发动机转矩；ne为发动机转速；be为发动机燃油消耗率；h为关于SOC 的二次代价函数；SOCr为预测时域内每一时刻的SOC 参考值；α为正的权重系数。

由于客观因素限制，电池SOC、电机转矩、电机转速、发动机转矩、发动机转速所受约束为：

由上述预测模型（9）、目标函数（10）和约束条件（11）组成的模型预测控制优化问题可采用动态规划进行求解。为了降低采用DP 求解的计算量，根据当前时刻的电池SOC 和控制量可能的取值确定SOC的可达范围，在此范围内对控制变量和状态变量进行离散化，利用Bellman 最优化原理在预测时域内逆向逐步求解最优控制律:

3 仿真验证及结果分析

仿真验证时选用的PHEV 主要参数为:整车质量为1 570 kg，滚动阻力系数为0.014，车轮半径为0.29 m，空气阻力系数为0.35，迎风面积为2.2 m2,主减速器速比为4.88，传动系数为0.92，发动机峰值转矩为130 N·m，电机峰值转矩为120 N·m，电池容量为30 A·h，额定电压为346 V。选取城市道路循环（Urban Dynamometer Driving Schedule,UDDS）工况作为样本工况并提取车速和加速度数据，采样步长取1 s，速度离散间隔取10 km/h，加速度离散间隔取0.3 m/s2，由式（8）可得不同车速对应的加速度转移概率矩阵。为验证基于模型预测控制的能量管理策略的有效性，在Matlab/Simulink 中进行仿真验证。

循环工况及PHEV 在5 倍工况下的电机、发动机转矩如图3 所示。PHEV 能够通过外部充电补充电池的电量消耗，且在电池SOC 约束范围内SOC 值对车辆动力性能无影响，为了充分利用电池电能采取电量消耗模式，使电池SOC 在循环工况结束时达到允许的最小值。选取预测时域为15 s，采样时间间隔为1 s，SOC 初始值为0.7，终值为0.5。图4 为基于MPC 的能量管理策略车辆工作模式柱状图和发动机工作点分布图。从图中可以看出电机的放电状态多于充电状态，且充电状态大多处于制动能量回收模式，电池电量得到了充分利用。发动机主要在转矩需求较大的加速阶段被启动，且发动机总体运行在高经济性区域。

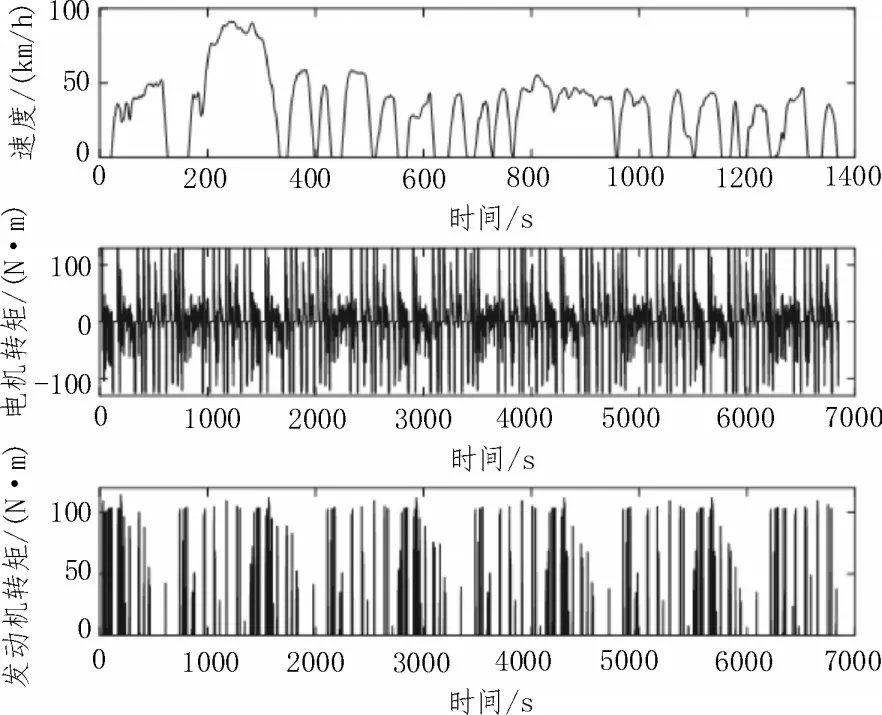
图3 UDDS循环工况及电机、发动机转矩

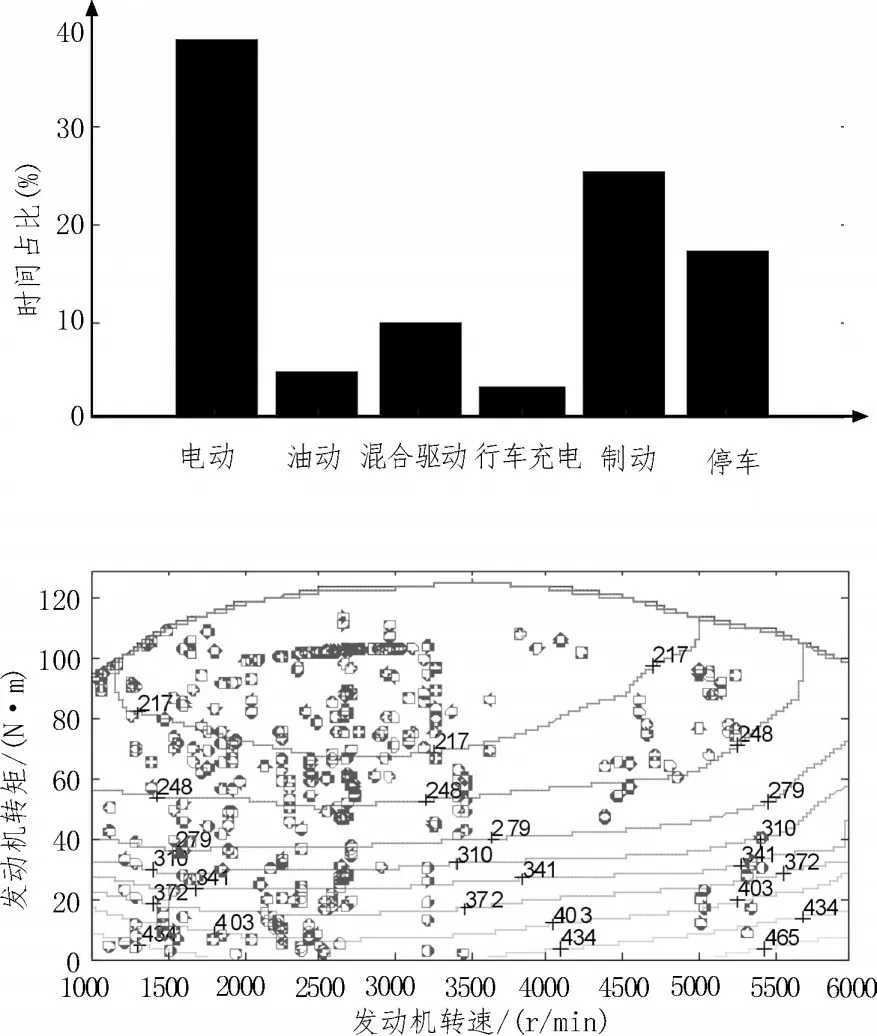
图4 工作模式时间占比及工作点分布

RC-MPC 策略与DP 能量管理策略、基于规则的能量管理策略和传统MPC 能量管理策略的电池SOC变化对比图和燃油消耗对比图如图5 所示。SOC 初始值为0.7，到达行程终点时各控制策略对应的SOC值分别为0.506 0、0.507 3、0.508 7、0.5220。忽略SOC变化量差异，在电池SOC 消耗模式，5 倍UDDS 路况的情况下，在RC-MPC 策略下车辆油耗为595.27 g，基于DP 的能量管理策略车辆油耗为575.77 g，基于规则的能量管理策略车辆油耗为768.39 g，传统的MPC 能量管理策略车辆油耗为666.40 g。该文提出的能量管理策略燃油经济性与基于DP 的策略效果接近，但是基于DP 的策略得到的是理想的优化结果，实际上无法实现，与基于规则的能量管理策略相比油耗降低22.53%，与传统的MPC 能量管理策略相比油耗降低13.64%。

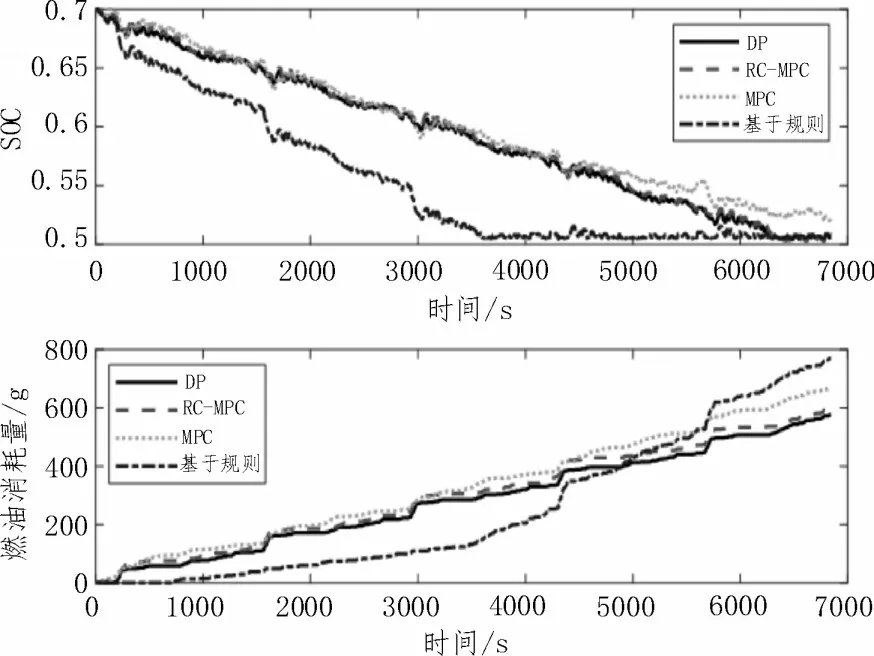
图5 各策略SOC曲线图及油耗曲线图

4 结论

通过基于DP 的模型预测控制策略，实现了对PHEV 转矩分配的有效控制。首先建立了PHEV 的能量消耗计算数学模型和电池组的一阶等效电路模型。其次将加速度的动态过程描述为随机马尔可夫过程，并根据UDDS 路况样本数据建立了加速度预测模型来预测加速度。然后基于理论参考轨迹，设计基于预测控制的PHEV 能量管理策略，并采用DP方法进行优化求解。最后仿真验证表明，车辆能够充分利用电能，使得发动机主要工作在高经济性区域内，与基于规则的控制策略相比具有更高的燃油经济性。该方法能够在PHEV 的能量管理中起到良好的效果。