2PPaPaR并联机构性能分析及优化设计

蒲志新 郭建伟 潘玉奇 白杨溪

辽宁工程技术大学机械工程学院,阜新,123000

0 引言

少自由度并联机构因定位精度高、负载能力强、可操作性好等特点而被广泛应用在工业领域中[1-2]。目前,3T1R并联机构作为少自由度并联机构中的一类,应用领域十分广泛,因此对此类并联机构的研究备受学者的关注。由PIERROT等[3]提出的四自由度并联机构是在Delta机器人基础上额外添加一条RUPU支链,从而增加了一组可绕固定轴转动的自由度。然而添加的此条运动支链在高速运动过程中会产生较大的磨损,为解决这一问题,孔民秀等[4]针对Delta-4机构的设计缺点提出一种改进的机构,将RUPU支链中的移动副用四边形连杆机构代替,有效地减小了传动过程中的摩擦,并分析了机构运行的可靠性。文献[5-8]介绍了一类由双动平台组成的3T1R并联机构,使末端执行器的转动范围有较大的增大。

3T1R并联机构的应用前景十分广泛,故研究其性能指标并进行优化设计对促进其性能的提高具有重要意义。在满足实际工况下可以通过遗传算法、粒子群算法、蚁群算法等优化方法,对各项性能指标进行优化以达到更优的效果[9-10]。李菊等[11]提出了三平移并联机构,以可达工作空间和能量传递效率为性能指标对机构进行参数优化设计。曾达幸等[12]基于主成分分析法对Delta机器人多维全域指标进行优化,验证了主成分分析法在并联机构尺寸参数优化求解中的有效性。周亚杰等[13]提出了一种具有高精度、高强度的3-PUS-PU柔顺并联机构,提出定位精度指标和紧凑性指标,对机构的几何尺寸参数通过粒子群算法进行优化设计,从而获得最优结构。

除此之外,并联机构在结构上也向着结构对称、构型简单的方向发展。文献[14-15]提出了一种由两条对称支链组成的并联机构,本文根据此类机构设计一种新型的2PPaPaR并联机构,以它为研究对象进行运动学分析,并以其可达工作空间、定位精度和可操作度为目标,通过粒子群算法对机构几何尺寸参数进行优化设计。

1 机构分析

1.1 构型分析

2PPaPaR并联机构简图见图1,该机构由定平台、动平台和两条对称分布的PaPa支链组成,其中,Pa是指平行四边形机构,由4个转动副组成。以其中一条支链为例进行分析,支链上端平行四边形机构(Pa)与主动移动副(P)相连接,沿直线导轨移动;支链下端平行四边形机构(Pa)与绕竖直方向转动的转动副(R)相连接,两条支链通过这两个转动副(R)与动平台连接在一起;支链上端平行四边形机构(Pa)与下端平行四边形机构(Pa)通过共用的一根连杆,刚性地连接在一起。主动副共有4个,分别为移动副B1、B2和转动副C12、C22。

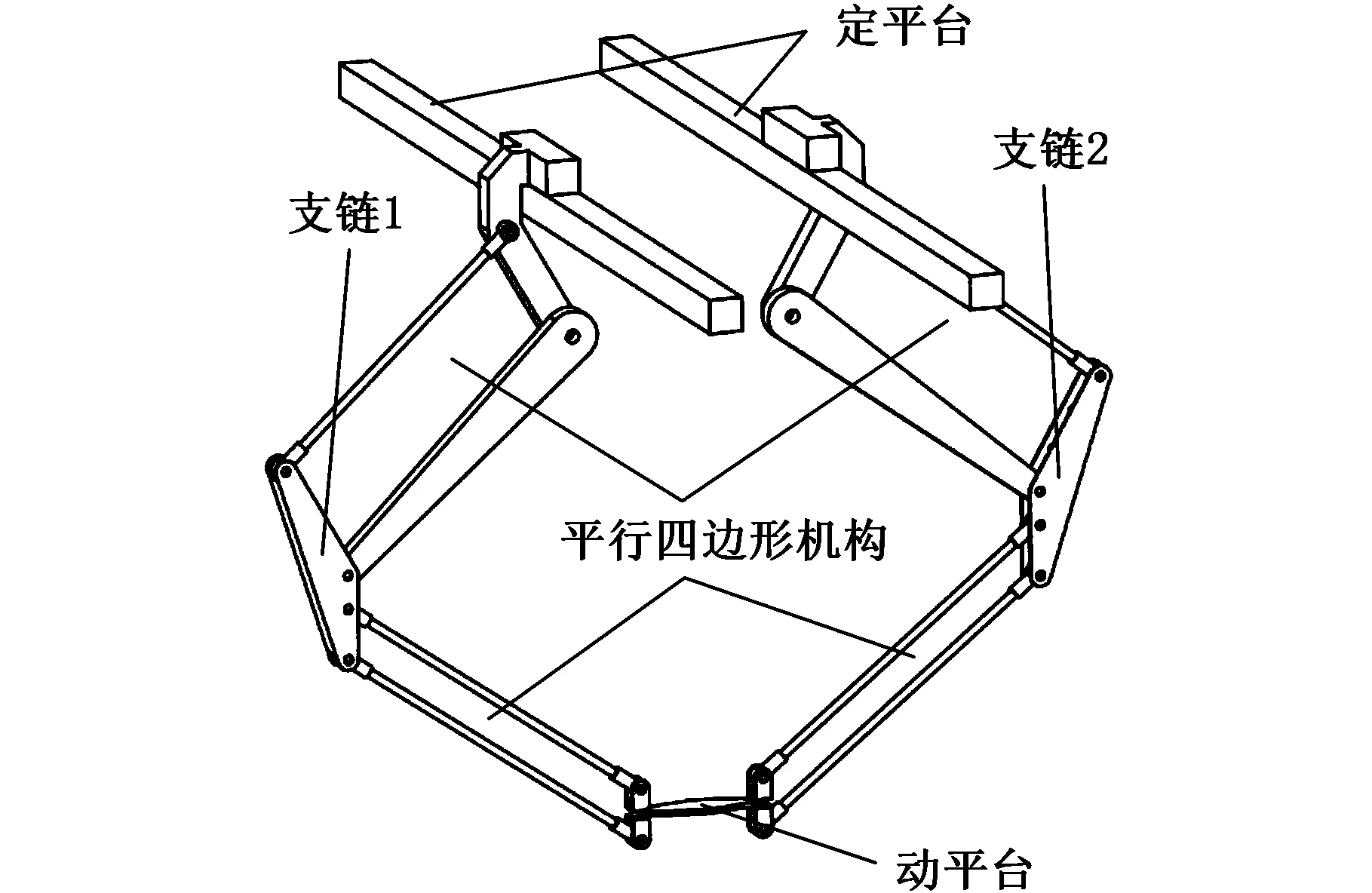
(a)2PPaPaR并联机构示意图

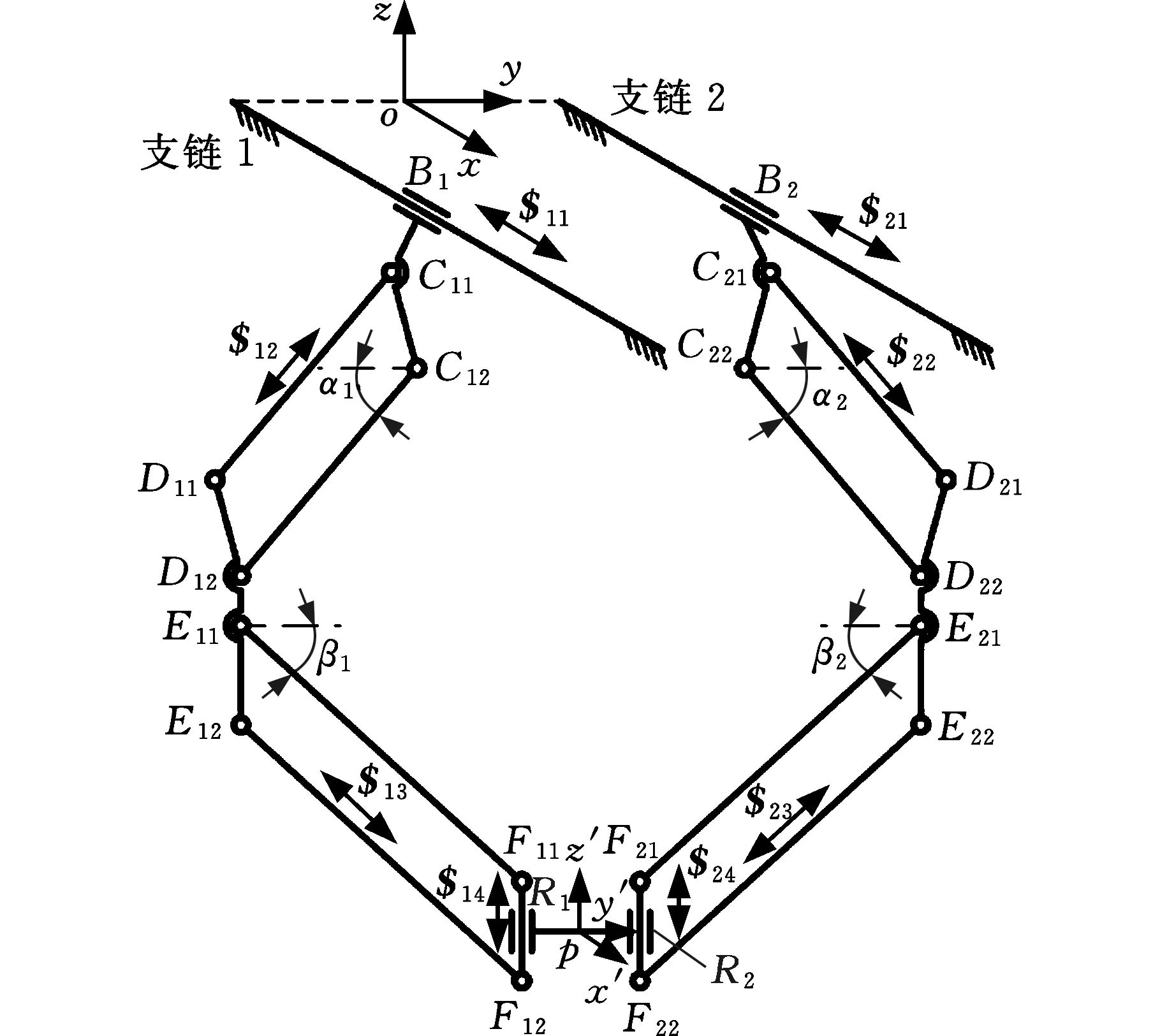
(b)2PPaPaR并联机构侧视图

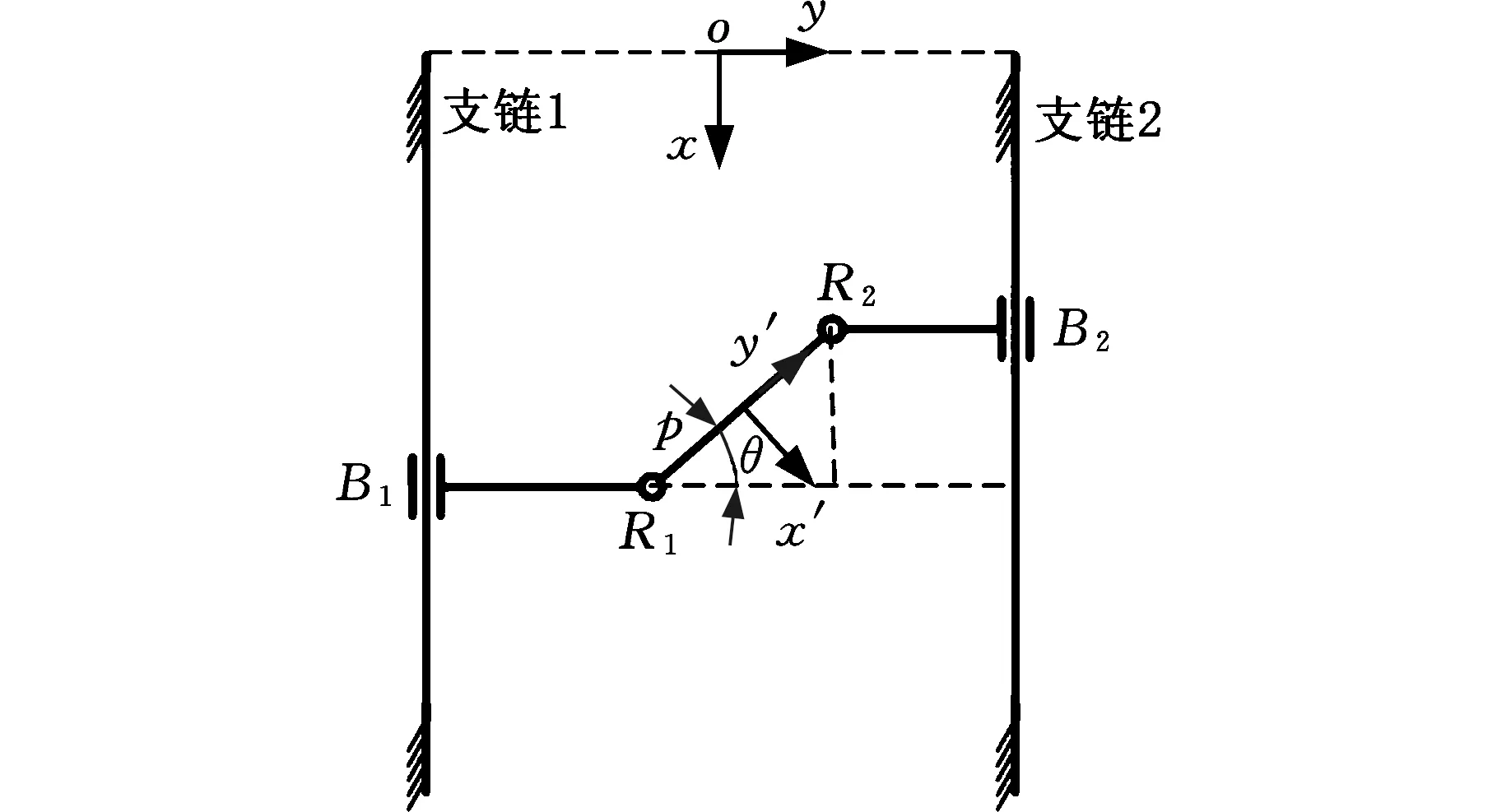
(c)2PPaPaR并联机构俯视图图1 2PPaPaR并联机构的结构简图Fig.1 Structural diagram of the 2PPaPaRparalleling manipulator

建立并联机构坐标系。定坐标系oxyz建立在定平台的两条平行导轨之间的起始端,原点o定义为两导轨起始端连线中点;x轴方向由导轨的起始端指向终止端;y轴位于导轨开始端的连接线上,方向由第一支链指向第二支链;z轴位于导轨起始端连接线中点竖直向上。同时在动平台的中心点处建立动坐标系px′y′z′,原点p位于动平台中心,三个轴的方向在初始条件下与定坐标系的轴线方向相同。该并联机构的结构参数如表1所示,其中i表示支链的编号,i=1,2。

1.2 自由度计算

各支链上运动螺旋的形式如图1a所示。在支链1上,$11为移动副B1的轴线方向,$12为连接定平台的四边形机构,$13为连接动平台的四边形机构,$14为转动副的转动轴线;在支链2上,$21为移动副B2的轴线方向,$22为连接定平台的四边形机构,$23为连接动平台的四边形机构,$24为转动副的转动轴线。对该机构支链1进行分析,其运动螺旋系可以表示为

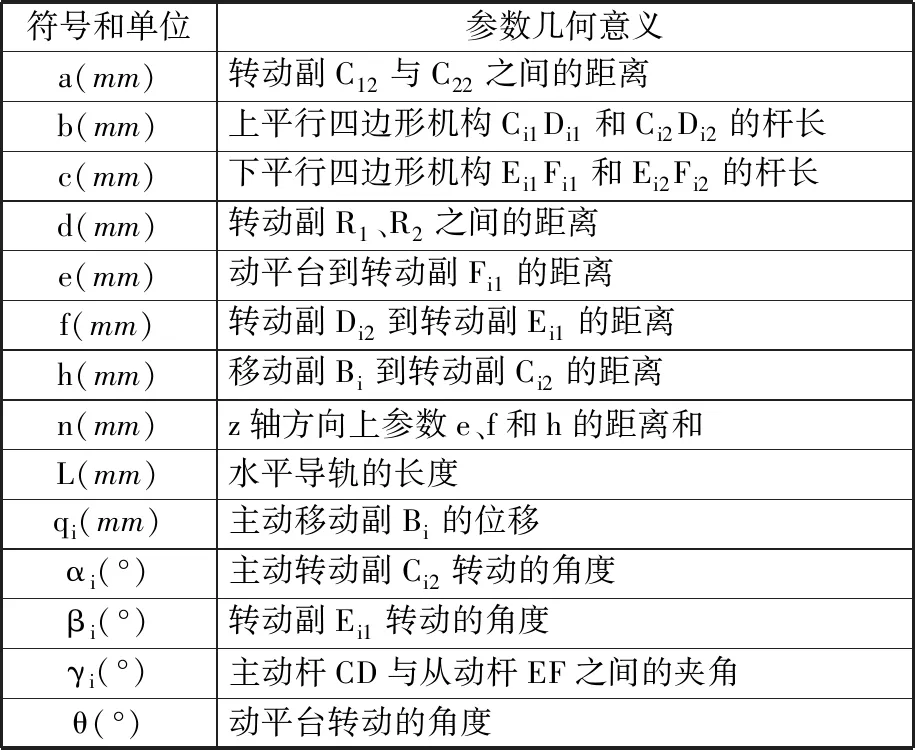
表1 2PPaPaR并联机构结构参数

(1)

根据运动螺旋与约束螺旋互易积为0的概念,计算第一支链的约束螺旋,具体表示为

(2)

同理,对2PPaPaR并联机构的支链2进行分析,其运动螺旋系可以表示为

(3)

对式(3)求其反螺旋,可得支链2的约束螺旋为

(4)

继续对式(2)、式(4)进行反螺旋求解,可得该机构的自由度性质及数量:

(5)

由式(5)可以看出,该并联机构具有4个自由度,并且在该并联机构中,动平台的运动方式为三移动一转动,分别是沿x轴方向、y轴方向和z轴方向的移动以及绕z轴的转动。

2 运动学分析

2.1 位置分析

位置分析的目的是为了找出输入参数与输出参数之间的关系,即分析主动副的输入量(q1,q2,α1,α2)与动平台的位姿(x,y,z,θ)之间的变换关系。通过分析2PPaPaR并联机构的运动特性,可得定坐标系到动坐标系的转换矩阵:

(6)

根据图1、表1所建立的并联机构坐标系以及结构参数的设置,可以得到点C12和点C22在参考坐标系oxyz中的坐标为

(7)

根据几何关系,动平台各个端点Ri在定坐标系oxyz中的坐标为

(8)

同时动平台各个端点通过动坐标系到定坐标系进行旋转变换,又可以得到另一种表达式,其端点Ri在动坐标系px′y′z′中的坐标为

(9)

将动平台端点Ri在动坐标系px′y′z′中的坐标通过转换矩阵转换得到其在定坐标系oxyz中的另一种坐标表达式:

(10)

将式(9)代入到式(10)的转换矩阵中可得

(11)

通过动平台端点Ri在定坐标系中的两种表达式,消去中间变量sinβi和cosβi,可以得到如下约束方程:

(12)

2.2 位置逆解

位置逆解是指当结构参数与动平台位姿(x,y,z,θ)确定时,对主动副位置(q1,q2,α1,α2)进行求解。

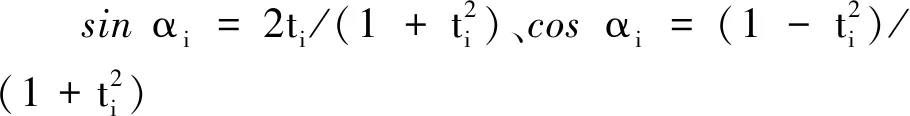
(13)

M1=y-dcosθ/2+a/2

M2=y+dcosθ/2-a/2

N=z+n

2.3 位置正解

位置正解是指当结构参数与主动副位置(q1,q2,α1,α2)确定时,对动平台位姿(x,y,z,θ)进行求解。

对约束方程式(12)解方程组可得4组关于位置正解的方程,经分析最终可以确定位置正解公式为

(14)

由式(14)可知,2PPaPaR并联机构的运动学分析较为简单。

2.4 正逆解算例验证

为了验证位置分析表达式的正确性,通过代入几组数据列出算例,分别进行运动学正解和逆解的验证。结构参数赋值如下:a=0.4 m,b=0.7 m,c=1.0 m,d=0.15 m,e=0.06 m,f=0.08 m,h=0.2 m,n=0.34 m。

根据式(13)、式(14)的运动学正逆解公式,通过MATLAB软件进行编程,取三组动平台位姿参数(x,y,z,θ)代入运动学逆解程序中,确定的主动副位置(q1,q2,α1,α2)如表2所示。然后将表2中求得的主动副位置(q1,q2,α1,α2)代入运动学正解程序中,可以求得动平台位姿(x,y,z,θ)的三组解,如表3所示。

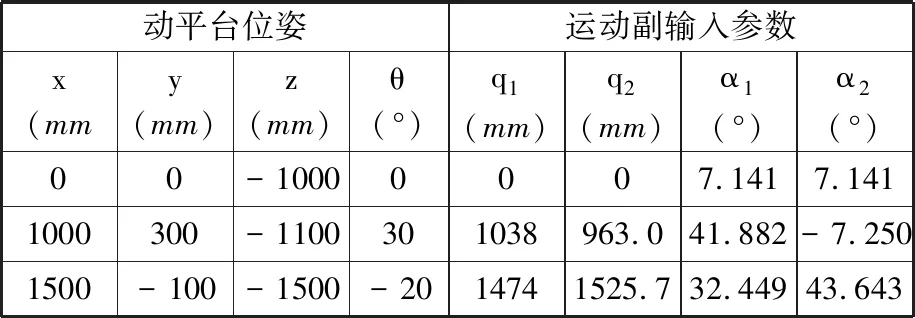
表2 位置逆解数值表

由表2与表3的数据可以看出,位置逆解算例和位置正解算例的结果相同,这验证了2PPaPaR并联机构的位置分析和正逆解公式的正确性。

2.5 工作空间

并联机构的性能优劣在很大程度上取决于其工作空间的形状及大小,因此并联机构的工作空间求解是十分必要的。

工作空间的求解较为复杂,且求解方法众多,其中基于位置逆解的求法是最为简单、实用的。本文采用数值法对工作空间进行研究,其搜索过程如图2所示。

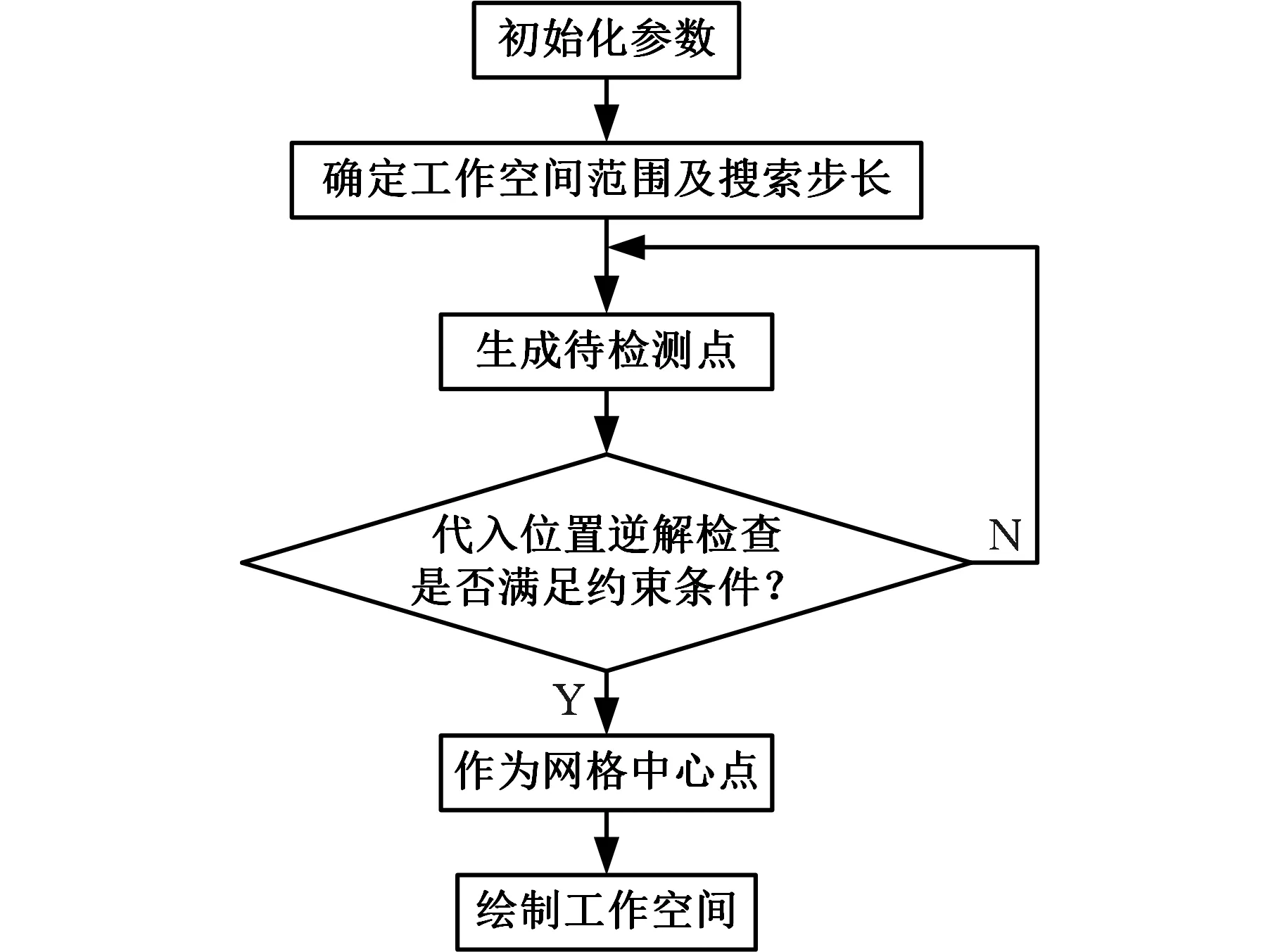
图2 工作空间搜索流程图Fig.2 Workspace search flowchart

为了更直观地了解2PPaPaR并联机构,根据对并联机构结构的分析,分别对其驱动副中移动副的移动距离和转动副的转动范围进行以下约束:

(15)

2PPaPaR并联机构相关的尺寸参数如表1所示,通过MATLAB编写工作空间搜索程序,进而求解得到机构工作空间,结果如图3所示。

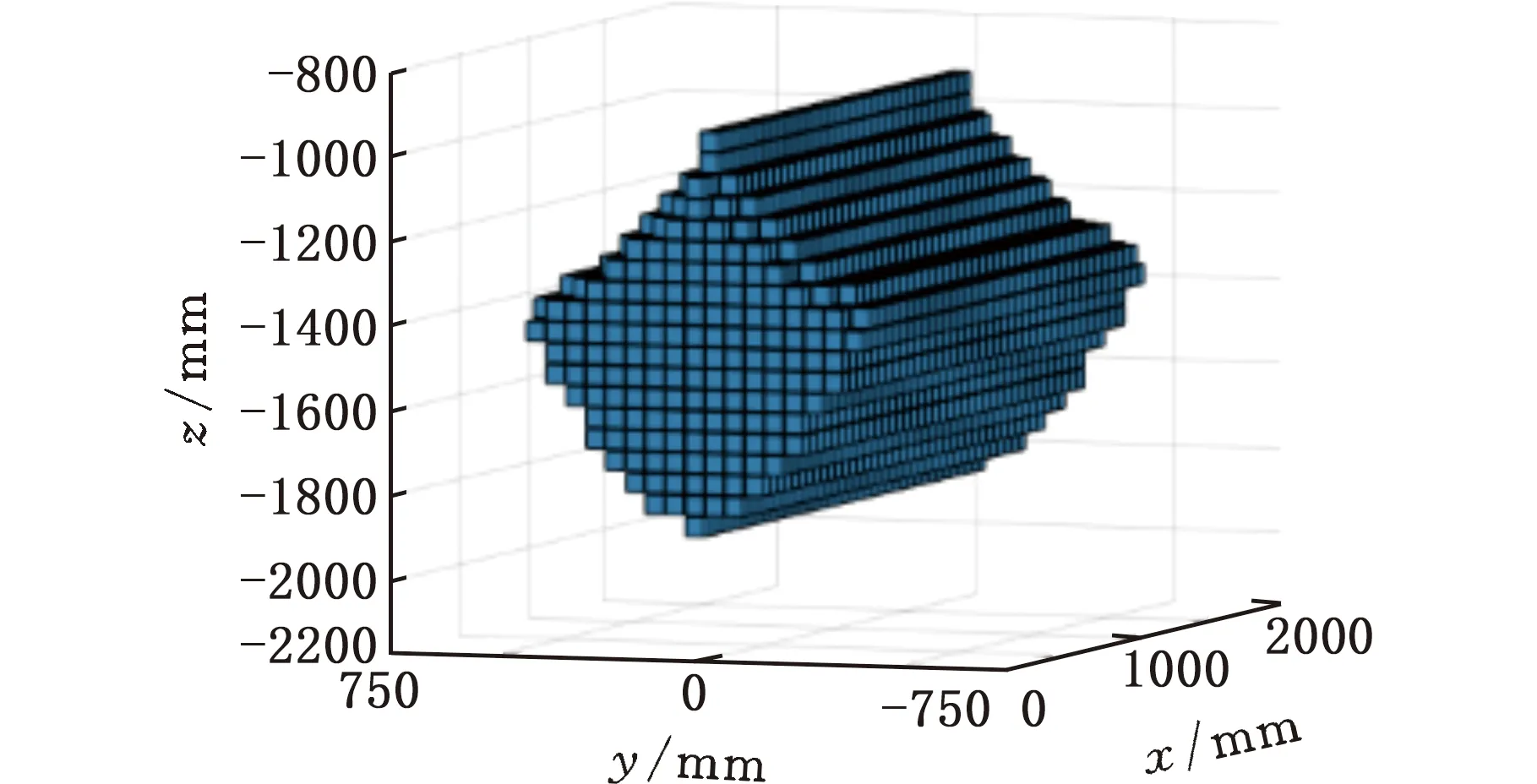
图3 2PPaPaR并联机构的工作空间Fig.3 Workspace of a 2PPaPaR parallel agency

由图3可以看出,2PPaPaR并联机构的工作空间近似由x=0处动平台中点能到达的区域沿x轴拉伸得到。该机构具有良好的工作空间对称性,这也表明该机构在实际条件下能够实现较好的位置调整功能。

3 奇异性分析

3.1 速度雅可比矩阵求解

速度雅可比矩阵是一个变换矩阵。建立各支链主动关节输入速度与末端执行器输出速度之间的映射关系,求得2PPaPaR并联机构的雅可比矩阵的数学关系式为

(16)

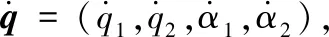
从该并联机构的构型参数中可以得到如下约束关系:

(17)

将式(17)对时间求导代入式(16)中,化简得

(18)

(19)

可以得到机构雅可比矩阵为

(20)

3.2 正向奇异

对矩阵Ja和Jb求取行列式得

(21)

当|Ja|=0、|Jb|≠0时发生正向奇异,称之为边界奇异。由式(21)可知:

(22)

由式(22)求解可得,驱动杆CiDi与输出杆EiFi的夹角γi=αi+βi中,至少有一条支链上的夹角γi=0或π。此时可分为三种情况进行讨论。

情况一:当γi=0时,有|Ja|=0,此时并联机构的第i条支链的驱动杆CiDi与输出杆EiFi向内折叠至平行,如图4a所示。

情况二:当γi=π时,也有|Ja|=0,此时并联机构的第i条支链的驱动杆CiDi与输出杆EiFi向外展开至平行,如图4b所示。

(a)γi=0

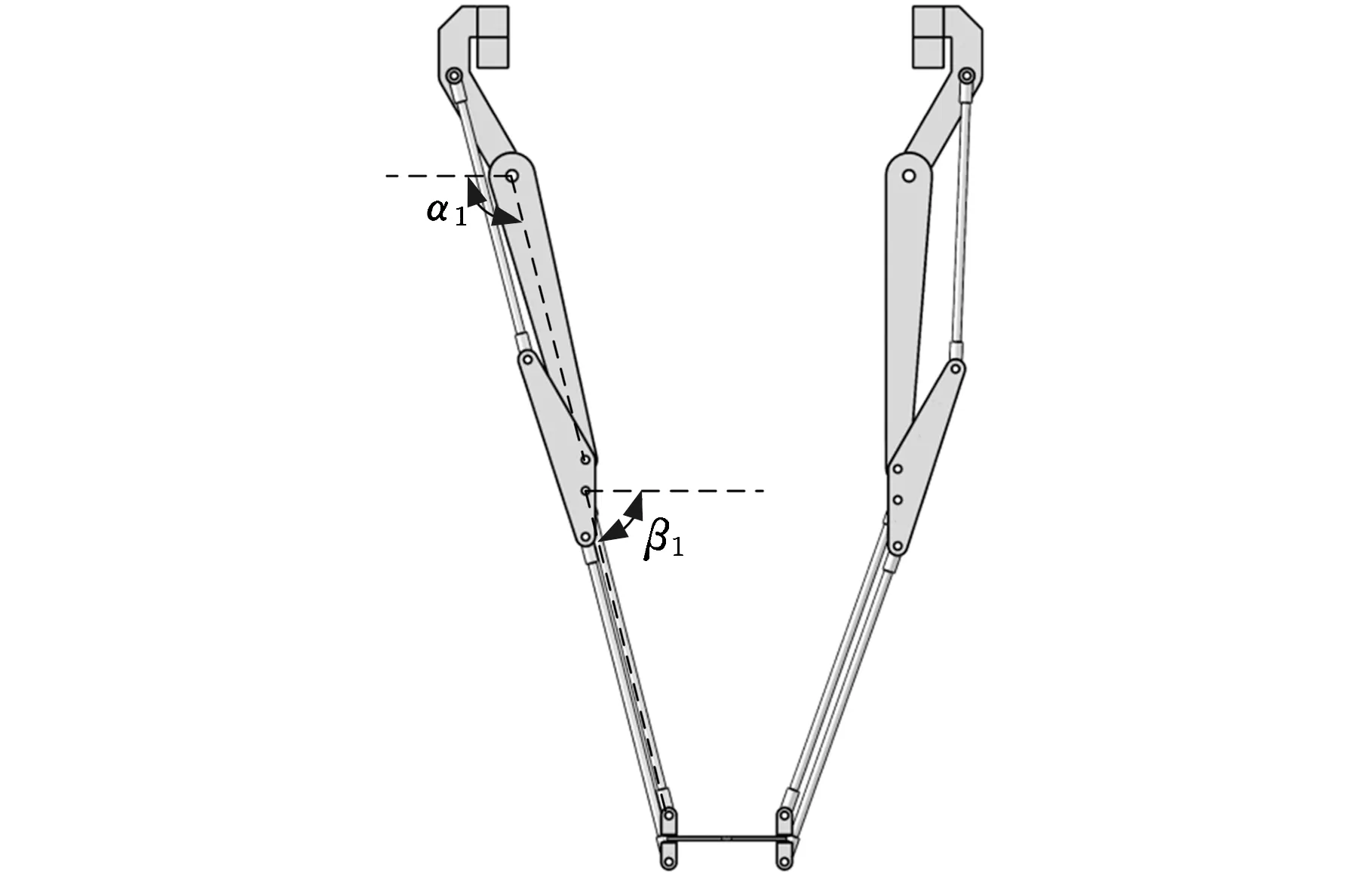
(b)γi=π图4 正向奇异Fig.4 Forward singularity

情况三:一条支链满足情况一,另一条支链满足情况二,此时机构会产生干涉现象。可以通过限制主动副C12和C22的转动角度α1和α2来避免此类情况的发生。

3.3 逆向奇异

当|Ja|≠0、|Jb|=0时发生逆向奇异,称之为位形奇异。由式(21)可知:

(23)

当式(23)成立时,同样分三种情况进行讨论。

情况一:结构尺寸d=0,即转动副R1和R2间距离为0,此时并联机构失去转动自由度,因此此种情况不做考虑。

情况二:当sin(β1+β2)=0时,输出杆E1F1与输出杆E2F2之间的夹角δ=π-(β1+β2)=0或π,驱动杆CiDi与输出杆EiFi不平行,逆向奇异如图5a所示。通过在其结构参数之间添加a+2b≤2c+d的约束关系,可以有效避免此类情况的发生。

情况三:当cosθ=0,即动平台转动角度θ=±π/2时,逆向奇异发生,如图5b所示,此类情况可以通过限制主动副B1、B2的相对位移来避免。

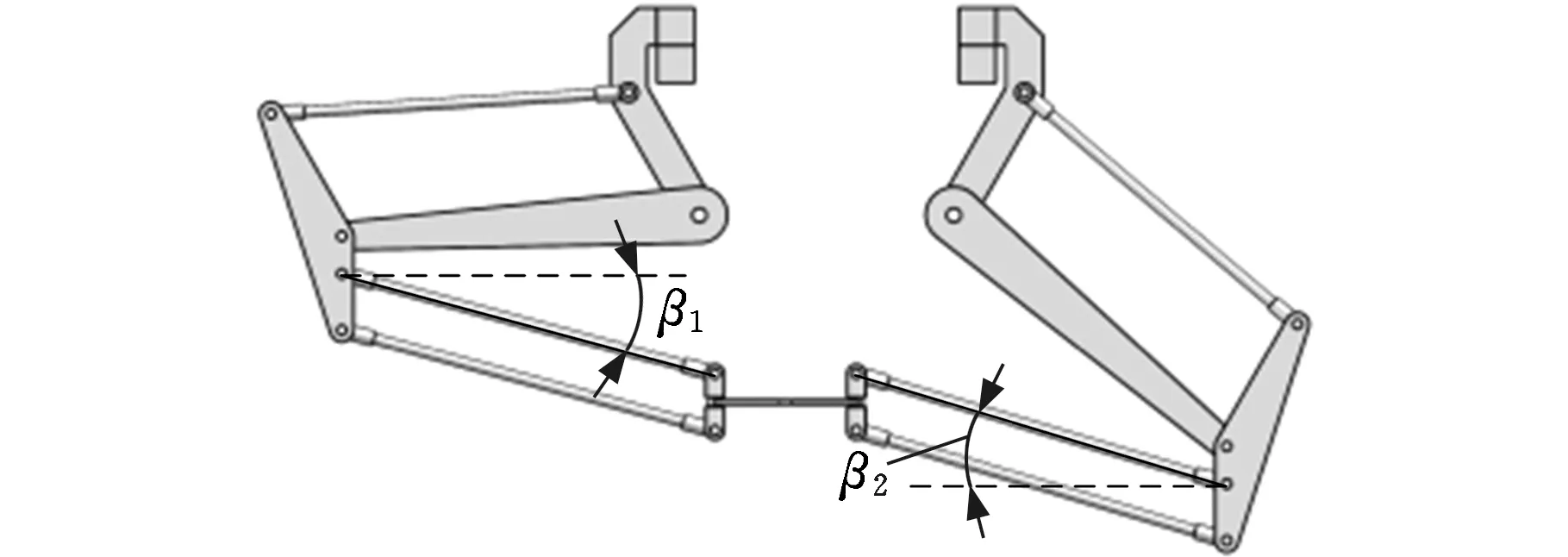
(a)δ=0

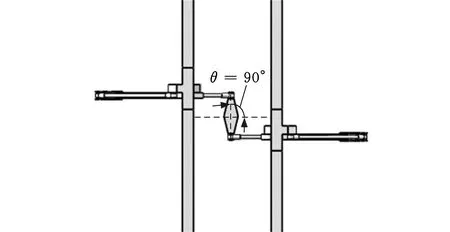
(b) θ=±π/2图5 逆向奇异Fig.5 Reverse singularity

3.4 混合奇异

当|Ja|=0、|Jb|=0时,发生混合奇异,称之为构形奇异,此时该机器人同时满足正向奇异和逆行奇异两种情况。受到机构的结构限制,此类情况很难实现。

4 性能指标分析

4.1 可达工作空间

可达工作空间性能指标可以直观地表达机构的工作空间大小。通过对机构工作空间的求解,可以得到机构工作空间内点的个数Wi,搜索点的个数设为Q,则可达工作空间的性能指标WV为

(24)

WV越趋近于1,其可达工作空间性能指标越好,工作空间体积越大。

4.2 定位精度

定位精度是并联机构重要的性能指标之一,对机构输入速度的偏差与输出速度的偏差进行运动学分析,可以得到误差放大因子为

(25)

其中,误差放大因子CJ可以代表机构的定位精度,CJ越小其定位精度越高;λmax、λmin分别为速度雅可比矩阵奇异值的最大值和最小值。

以x=1000 mm处y∈[-300,300]mm、z∈[-1800,-900]mm的二维平面为例,绘制定位精度指数分布情况,如图6所示,可以看出定位精度具有对称性,与机构结构特征吻合。

为衡量机构在工作空间全域下的定位精度,引入全局条件数:

(26)

4.3 可操作度

可操作度性能指标是指动平台在可达位置工作空间内变化位姿的能力,是并联机构性能分析中的重要部分。通过分析并联机构的速度雅可比矩阵,选取可操作度评价指标ωJ作为并联机构可操作度性能指标:

(27)

可操作度评价指标ωJ为1时,并联机构的可操作度为最佳;若可操作度评价指标ωJ趋于0或者无穷时,机构趋向于奇异位置。再次取中间位置x=1000 mm处的平面,绘制可操作度指数分布如图7所示,可以看到,可操作度指数也呈对称性分布,且与机构特点相符。

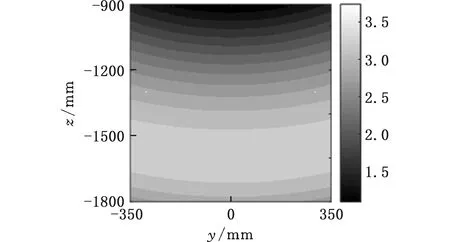
图7 可操作度指数分布图(优化前)Fig.7 Actionability exponential distribution plot (before optimization)

机构在工作空间全域下的可操作度为

(28)

5 优化设计

5.1 数学模型建立

5.1.1设计变量

通过2PPaPaR并联机构各性能指标分析可以看出,尺寸参数中,a、b、c、d(图1和表1)对各性能指标的影响最为明显,因此在优化设计中取尺寸参数a、b、c、d为设计变量。

5.1.2目标函数

对于并联机构,在满足设计要求的前提下,通常希望得到最大的工作空间和最优的工作性能。对于上节提出的可达工作空间性能指标、全域定位精度指标和全域可操作度性能指标,可利用参考目标距离法,将三个目标函数转化为一个单目标函数,该方法类似于将多个目标进行同向化处理,应用简单且广泛。采用该方法可将目标函数定义为

(29)

式中,Zi为目标函数参考值。

5.1.3约束条件

根据2.4节对并联机构结构参数的赋值,给出了2PPaPaR并联机构各设计参数的尺寸约束范围,如表4所示。

表4 设计参数的约束范围

为了避开奇异位形和干涉情况,设计变量需满足以下约束条件:

(30)

5.2 优化算例

粒子群优化(particle swarm optimization,PSO)算法是一种仿生算法,其全局收敛性与遗传算法(genetic algorithm,GA)相近,但它具有更快的收敛速度,因此本文选用PSO算法作为优化方法。

利用粒子群算法进行优化求解时,其优化的结果会因为定义的参数不同而改变。经过不断调试后,最终确定本次优化求解的参数配置如表5所示,通过MATLAB进行编程计算,目标函数收敛过程如图8所示,最终得到的优化结果如表6所示。

表5 粒子群算法参数设置

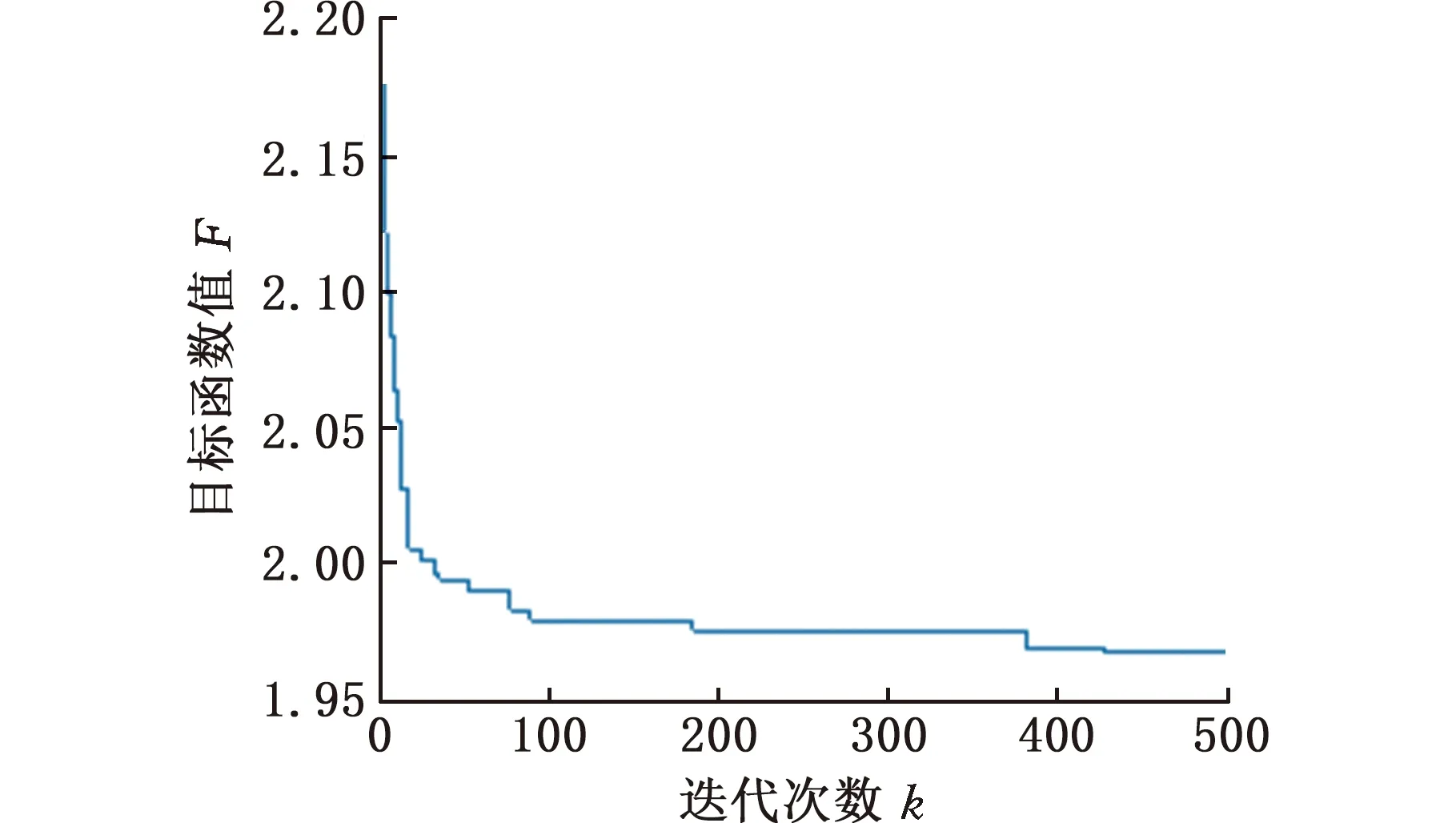
图8 目标函数随迭代次数变化曲线Fig.8 Curve of objective function with number of iterations

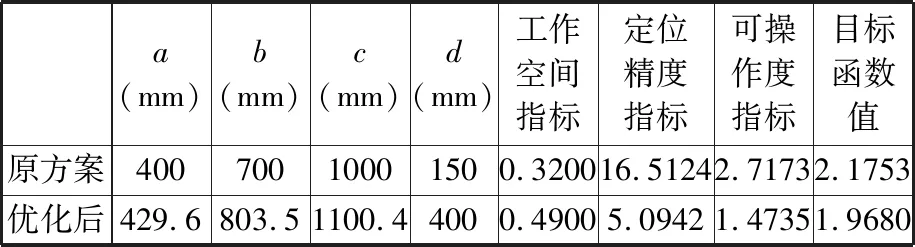
表6 粒子群算法优化结果

由图8可以看出,目标函数逐渐趋于某一固定值,并在之后保持不变,经过428次迭代优化结果达到最佳。

由表6可以看出,在运用粒子群算法对2PPaPaR并联机构优化求解后,机构转动副C12与C22之间的距离a和动平台转动副R1、R2之间的距离d都有所增大,从动杆的杆长b有所减小,通过计算,机构可达工作空间性能指标提高了53%,全域定位精度指标提高了74%,全域可操作度指标提高了46%,为机构尺寸参数设计提供了参考。

5.3 结果对比

由于机构在实际加工中,其精度和制造成本会受到限制,因此将优化后的设计参数圆整,得到一组新的机构参数为:a=430 mm,b=800 mm,c=1100 mm,d=400 mm。依据此参数重新对并联机构的工作空间进行计算,结果如图9所示。

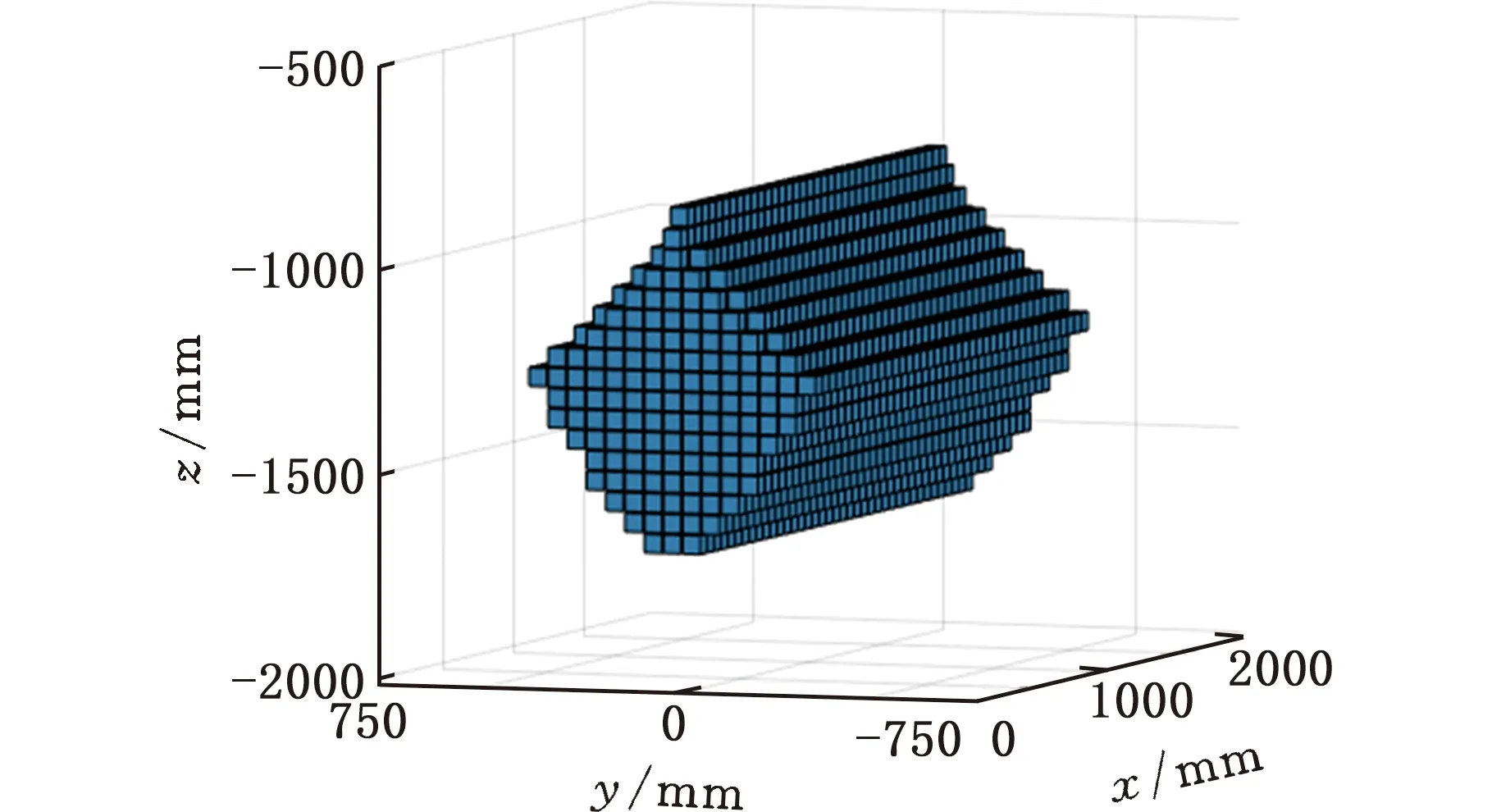
图9 机构优化后的工作空间Fig.9 The workspace after the organization is optimized

同样取中间位置x=1000 mm处的二维平面,绘制优化后的定位精度指数分布如图10所示。对比图6可以发现,定位精度指标得到了明显的提高,在工作空间内均小于8.5。

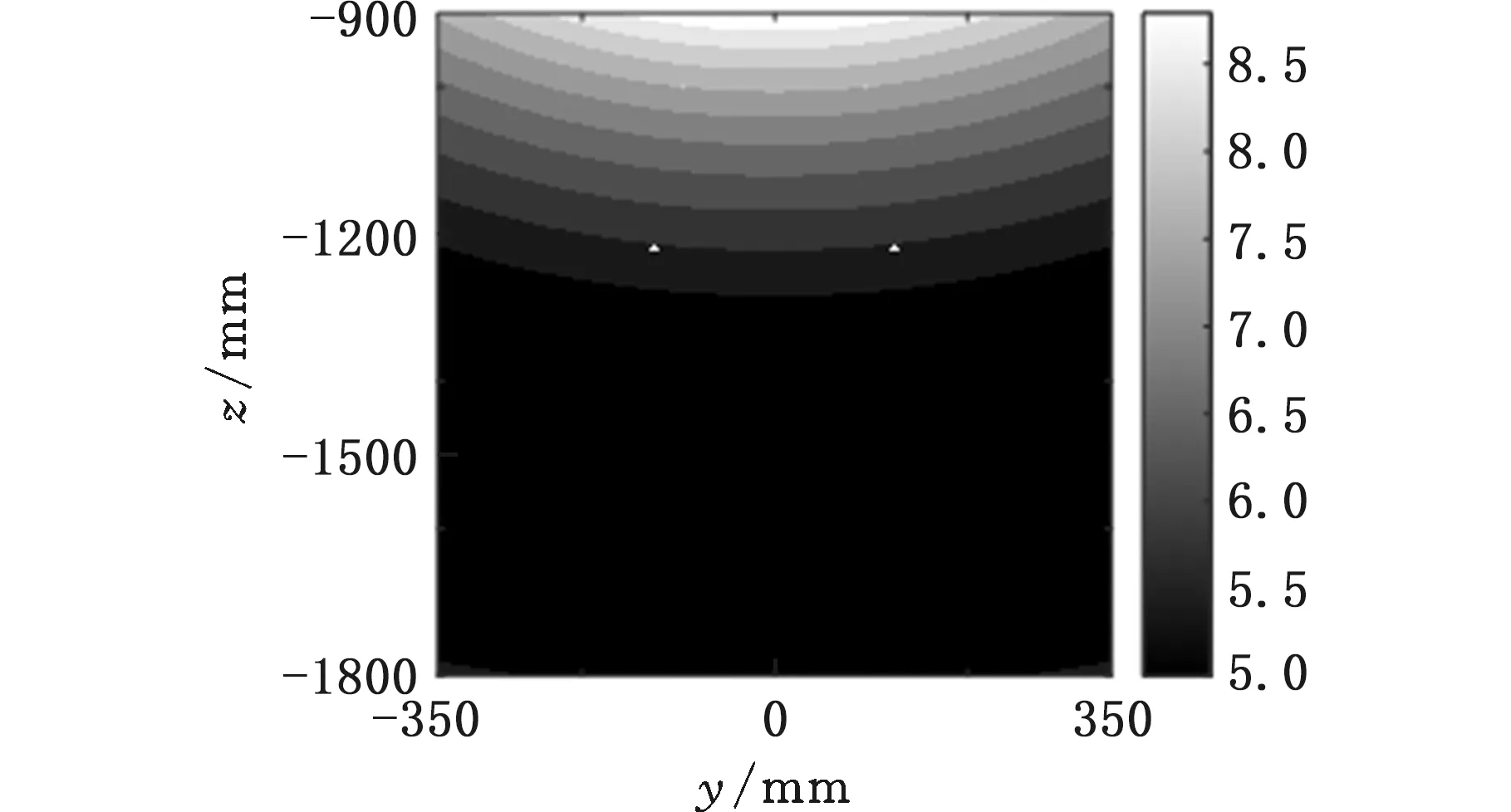
图10 定位精度指数分布图(优化后)Fig.10 Positioning accuracy index distribution (after optimization)

图11所示为尺寸优化后机构的可操作度指数分布情况,可以发现整个平面在x=1000 mm处的可操作度均趋近于1,对比图7可以发现其可操作度性能也得到了明显提高。

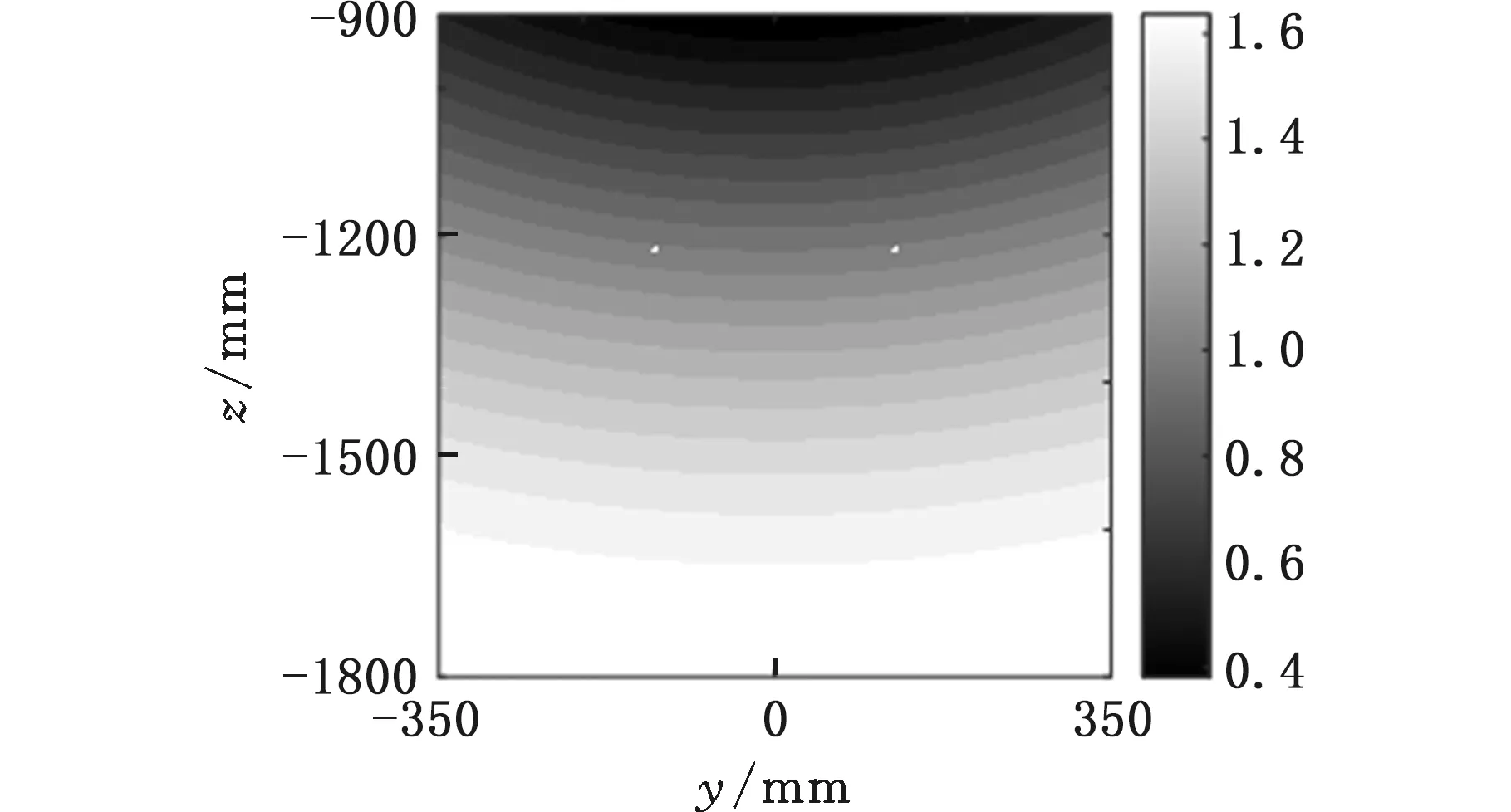
图11 可操作度指数分布图(优化后)Fig.11 Actionability exponential distribution plot (after optimization)

6 结论

(1)提出了一种新型的3T1R并联机构,该机构具有结构简单、构型对称、工作空间大、灵巧度好等特点。

(2)建立了机构的运动学模型,基于闭环矢量法求解了其运动学的正逆解,然后求解了工作空间,并对机构的奇异性进行分析。

(3)分析了机构的可达工作空间性能指标、定位精度指标和可操作度性能指标,并利用粒子群算法以三个指标为目标函数,对机构的结构尺寸进行了优化设计,得到了较优的机构尺寸参数,同时机构的性能指标有了明显提高,为样机的搭建奠定了基础。