突出“两个过程” 突破关键能力
——以“一类曲线的切线问题复习探究”为例
林 威, 姚佩峰
(1.余杭高级中学,浙江 杭州 311100;2.瓶窑中学,浙江 杭州 311115)
1 问题缘起
通过对近几年全国高考数学卷的分析,笔者发现过定(动)点向曲线作切线这一类题目经常出现在选择题和填空题中.曲线涉及的类型有指数函数、对数函数、对勾函数、三次函数等,涉及的圆锥曲线有椭圆、双曲线、抛物线,涉及的知识点较多,解题方法灵活多变,充分考查了学生的数学抽象、逻辑推理、数学运算等核心素养.本节课以“一类曲线的切线问题复习探究”为例,突出两种方法(设切点解方程和数形结合找区域),重点探究过不同区域的点是否可以作曲线的切线以及可以作多少条切线的问题,为学生解答类似问题提供一个新的视角.
2 教学方法的选择
本节课以问题链探究的方式:从问题1开始,设计一系列问题(问题2~9)引发学生探究,用代数方法和信息技术手段进行双重验证,然后类比迁移到一般情况下结论是否成立,再拓展研究其他曲线的情况.数学课堂教学不仅要让数学知识发生发展的过程合理,也要让学生在参与学习过程中认知的过程、思维的过程合理[1](以下统称“两个过程”)是本节课设计的关键.笔者通过使用信息技术,让学生直观感受过定点作双曲线切线的动态变化,将数学思维的发生和发展过程充分地暴露在学生面前,吸引学生积极参与知识的再创造和发展的过程[2],在问题解决的过程中培养了学生的关键能力.
3 课堂实录
3.1 问题引入
问题1已知双曲线x2-y2=4,过点(-1,0)可以作双曲线______条切线.
分析运用方程的思想,根据直线与圆锥曲线的位置关系,学生列式求解,得到结果.这类求解是学生最熟悉的.
设切线方程为y=k(x+1),联立
得
(1-k2)x2-2k2x-k2-4=0.
当1-k2=0时,k=±1,显然所得直线不是双曲线的切线,故k≠±1.由Δ=0,得
(-2k2)2+4(1-k2)(k2+4)=0,
整理得
从而
因此过(-1,0)可以向双曲线左支作两条切线(如图1).
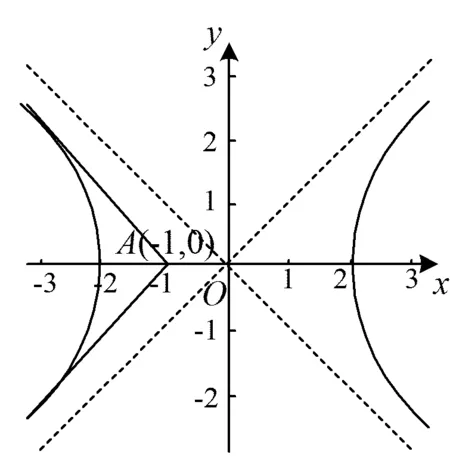
图1
在课堂的实际教学中,学生解方程过程中往往会忽视二次项系数为0的情况,要验证当k=±1时的直线是否为双曲线的切线.
设计意图从特殊到一般,从熟悉到未知,从学生知识和方法的最近发展区出发,求过特殊点作双曲线的切线,让学生温习直线与圆锥曲线位置关系的代数求解方法,让学生从已知的知识结构入手,激发了学生进一步学习和探究新知识的欲望,为进一步研究在平面直角坐标系中不同区域的点作双曲线的切线提供认知和学习心理,让求知和探索自然而然地发生.

分析这个问题仅仅是把问题1中的点(-1,0)改为(-1,1),学生很容易列式求解.
设切线方程为y-1=k(x+1),联立
得
(1-k2)x2-2k(k+1)x-(k+1)2-4=0.
当1-k2=0时,k=±1,显然所得直线不是双曲线的切线,故k≠±1.由Δ=0,得
[-2k(k+1)]2+4(1-k2)[(k+1)2+4]=0,
整理得 3k2-2k-5=0,


图2
追问1若点为直角平面上任意一点,过点可以向该双曲线作几条切线呢?
设计意图问题2是问题1的一个变式,让学生思考点的位置变化对代数方程的求解产生的影响.方程的系数为0引发了学生的认知冲突,通过数形两个角度进行操作确认,直观感知下的操作确认通过GeoGebra软件进行动态演示,验证猜想,把抽象内容可视化、静态内容动态化,真实地展示学生的数学思维发生和发展过程.有思维冲突才有进一步深入思考的可能,从而培养了学生数学运算、逻辑推理、直观想象的核心素养,为学生进一步探究提供了知识、认知和思维的准备.
3.2 从特殊到一般

如图3,渐近线和双曲线将直角坐标平面分成多个区域.学生给出以下猜想:
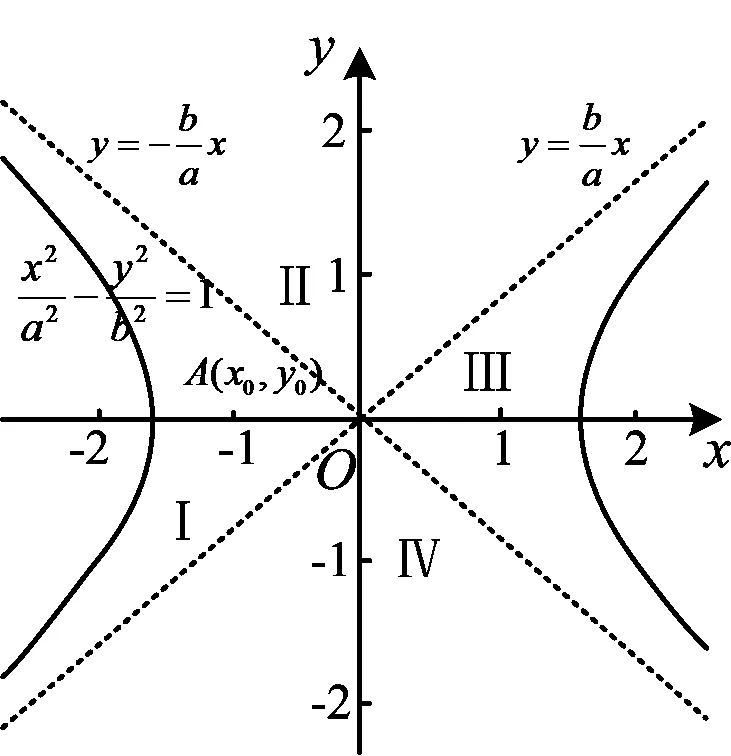
图3
1)当点在区域Ⅰ内时,通过点可以向双曲线左支作两条切线;
2)当点在区域Ⅲ内时,通过点可以向双曲线右支作两条切线;
3)当点在区域Ⅱ,Ⅳ内时,通过点可以向双曲线左右两支各作一条切线;
4)当点在渐近线上时(除原点),通过点可以向双曲线相近的一支作一条切线;
5)当点在原点时,无法向双曲线作切线.
给学生充分的时间思考、讨论、计算,最后教师给出答案(过程略).
评注学生在理解运算对象的基础上提出运算问题,探究运算思路,选择运算方法,进而求得运算结果.不过这里的运算量比较大,分类讨论和代数式的化简对学生来说都是挑战,有些学生遇到代数式的化简就会“缴械投降”,此时教师应当鼓励学生继续算下去,敢于“硬碰硬”,这样有助于学生运算能力的提升.
设计意图让学生在问题链的指引下,由特殊到一般,思维层层递进;从代数方法到几何直观,在研究“切线条数”这个问题上认识到几何直观的优越性;通过几何直观总结规律,运用代数方法小心求证,对问题的理解会更加深刻.在问题求解的过程中提升了数学运算、数学抽象、逻辑推理、直观想象等核心素养.通过对这个猜想的证明,学生从之前的几何作图的操作阶段进入到代数运算的逻辑推理阶段,证明的过程让学生体会了合理建立解析几何数形对应的必要性,整个证明过程让学生的数学思维再一次得到发生和发展.

方法1设切线方程为y-2=k(x-2),联立
得
(a2-k2)x2+4k(k-1)x-4(k-1)2-a2=0.
当a2-k2=0时,k=±a,所得直线不是双曲线的切线,故k≠±a.由Δ=0,得
16k2(k-1)2+4(a2-k2)[4(k-1)2+a2]=0,
整理得
3k2-8k+4+a2=0.
过点(2,2)能作该双曲线的两条切线,则
Δ1=64-12(4+a2)>0,
从而

评注利用直线和圆锥曲线的位置关系,联立方程求解,思维简单,符合学生的认知起点.但对学生来说计算量较大.
方法2(作图象找区域)由上述结论可得点(2,2)在双曲线外部,且不在双曲线的渐近线上,从而
得
故
设计意图让学生比较两种运算方法,巩固探究成果.
3.3 拓展探究:从双曲线到其他曲线
3.3.1 以飘带函数为载体

( )

(2023年浙江省杭州市一模数学试题第8题)
答案:B.
3.3.2 以指数函数为载体
问题6若过点(a,b)可以作曲线y=ex的两条切线,则
( )
A.eb C.0 答案:D. 3.3.3 以对数函数为载体 问题7若直线y=ax-1(其中a>0)与曲线f(x)=ln(x+b)相切,则实数b的取值范围为______. 3.3.4 以三次函数为载体 问题8已知a>0,若过点P(a,b)可作曲线y=x3的3条切线,则 ( ) A.b<0 B.0 C.b>a3D.b(b-a3)=0 答案:B. 3.3.5 以其他含有拐点切线的函数为载体 问题9已知函数f(x)=ex-1+lnx,则过点(a,b)恰能作曲线y=f(x)的两条切线的充分条件可以是 ( ) A.b=2a-1>1 B.b=f(a) C.2a-1 答案:AD. 评注以这5类函数为载体的研究切线条数的问题都可以通过作图象找区域解决,关键是要发现影响区域划分的渐近线、拐点处的切线等,比设切点解方程要简洁明快. 本节课是一节微专题复习拓展课.大多数教师喜欢直接给出结论,然后让学生利用结论训练自己的解题能力.但笔者认为从学生的可持续发展来看,探究结论形成的过程,挖掘结论证明的价值,培养学生发现和提出问题、分析和解决问题的能力是对学生未来数学学习的一种投资. 在结论形成的过程中,充分发挥信息技术的作用,通过几何直观的建立,让学生感受解析几何的数形对应.以数学的方式循序渐进,充分暴露数学思维的发生和发展过程,让学生从已有的知识与方法体系出发通过再创造和发展不断完善与提升,构建更完整的知识与思想方法体系.在问题解决的过程中,自然而然地用数学的眼光观察现实世界,用数学的思维思考现实世界,用数学的语言表达现实世界. 在结论验证过程中,重视学生代数运算能力的培养,从数学本质出发,鼓励学生有“硬算”的勇气,看似最笨的办法实则是我们解决问题最大的依赖.在硬算的基础上多角度寻求运算的优化,代数运算的分类讨论以及逻辑推理的过程使学生更规范地思考问题、更严谨地解决问题、更深刻地感悟问题的本质,培养了学生良好的思维品质和科学精神,从而使学生的运算素养得到进一步的发展. 数缺形时少直观,形缺数时难入微.数形结合的思想是高中数学很重要的一种思想方法,借助几何直观感知所研究问题的形态与变化,利用几何图形描述和分析数学问题,建立代数与几何图形的内在联系[3],构建数学问题求解的直观模型,渐近线、拐点切线、曲线是划分区域的关键,可以助力问题求解. 习题课是高中数学课堂教学中一个重要的课型.习题课的教学需要“价值引领、素养导向、能力为重、知识为基”,试题的选择要“源于教材,高于教材,题在书外,根在书内”,要设计具备典型思想和方法的问题链.好的问题与变式应该是基于情境、思想丰富、知识完备、思维深刻,以数学思维为核心,从学生的学情出发,符合学生知识基础、能力基础和认知规律.好的数学问题与变式能让“两个过程”更到位,学生带着问题进课堂,想着更多的问题出课堂,思维能力在感悟问题本质中升华,解题后意犹未尽,回味无穷. 问题链教学要以学生为中心,从基础题和教材原题入手,兼顾每一名学生的认知水平,让每一名学生都能有所写、有所想、有所思.问题链的设计并非随意拼凑、杂乱无序,而是一个将问题合理设计安排、环环相扣的过程.探寻试题的“源”与“流”是问题链设计的基本前提,提升学生的数学思维和素养是问题链教学的核心目标,揭示问题的数学本质是问题链教学的顶层追求.通过问题链逐步将学生的思维引向深入,从低阶思维向高阶思维不断发展,促进学生的深度学习,为培养学生的数学学科核心素养(如直观想象、数学抽象、逻辑推理、数学建模等)奠定坚实的基础.
4 反思与感悟
4.1 培养直观想象能力
4.2 微专题的复习课建议
4.3 问题链探究设计的思考

