基于改进双层鲁棒的氢-电混合时间尺度联合储能系统规划
刘倩,贾健雄,靳幸福,孙博,王馨,王磊
(1.国网安徽省电力有限公司经济技术研究院,合肥 230031; 2.合肥工业大学 电气与自动化工程学院,合肥 230009)
0 引 言
为达成我国“双碳”目标,光伏和风电等可再生能源发电近年来呈爆发式增长态势[1]。截至2021年底,我国光伏和风电累计装机容量分别达3.06亿千瓦和3.28亿千瓦,占全国同期总发电装机容量的12.9%和13.8%。按照《2030年前碳达峰行动方案》要求,预计我国光伏和风电的装机容量在2030年将达到12亿千瓦以上。具有明显季节性供给特征的光伏和风电等新能源发电的高比例并网,加大了与同样具有季节性需求特征的用电负荷之间的不匹配程度,导致电力系统季节性电力电量不平衡问题愈加凸显[2-3]。为此,当前广泛采用火电、水电及电化学储能等灵活性资源对电力系统的供需矛盾进行调节。然而,不明确的电力辅助服务市场机制严重阻碍了火电参与电力系统调峰调频的积极性[4-5];受自然资源和地理位置的限制,水电难以实现电力系统大范围的电力电量调节[6-7];作为当前发展较快的一种灵活性资源,电化学储能的全面推广受投资成本及市场机制约束[8-9]。最为关键的是,上述电力系统的灵活性资源调节多为日时间尺度,无法参与季节性的电力电量平衡。为应对高比例可再生能源季节性出力波动,理想的季节性储能应具备存储容量大、储能单位成本低、使用寿命长、长期尺度下能量转换效率高的特点。相较于常规灵活性资源,利用电解水制氢的季节性氢储能具有长时间尺度、大空间范围内的电力电量调节能力,能够实现储能在广域时空范围内的能量转移(换),技术经济效益显著,受到了业界的广泛关注。
目前,针对季节性氢储能系统已有部分研究。在季节性氢储能建模方面,文献[10]基于季节性储能的一般数学模型,建立了氢储能系统的动态特性模型;文献[11]采用广义能量-物质流矩阵描述了季节性氢储能运行特性,为统一能源系统的建模奠定了基础;文献[12]提出了具有季节性储能的HSC-EN(氢供应链-电网)概念以解决可再生能源与氢需求的时空不匹配问题,建立了电解槽和季节性储能的最优投资模型;文献[13]提出了两种季节性储能建模的优化方法。在优化规划方面,文献[14]在每个季度内选取一个典型日进行聚合和排序,但这将导致对电力电量变化的描述不充分;文献[15]引入了多时间网格法对季节性储能系统的运行进行优化,然而其规划模型中采用的仍然是全时间序列,故优化规划问题工作量的减少有限;文献[16]提出了一种基于典型日间和日内状态叠加的储能系统建模方法,尽可能的保留了原始数据的时序性;文献[17]利用改进的层次聚类分别对小时、天、周进行聚类,建立了考虑日内和日间电储能的电力系统最优扩展规划模型;
季节性氢储能涉及到的长时间尺度增加了系统优化规划的计算量,而目前大多文献均将传统的、短期的典型日优化规划方法延伸至长时间尺度的季节性氢储能优化规划,造成了典型日间能量的不连续。如何使断续的典型日间能量连续(也即典型日间耦合)以及如何在模型中将短时间尺度与长时间尺度的储能技术进行有效耦合也是未来亟需解决的一个问题[18-20]。文中针对季节性氢储能的优化规划,通过建立氢-电耦合系统数学模型,采用长-短期融合的氢-电联合协同储能机制,开展了双层鲁棒优化和典型日间耦合的研究,针对不同应用场景进行了算例分析,验证了所述方法的可行性和有效性。
1 氢-电联合储能系统的数学模型
氢-电联合储能系统主要由电气部分和氢气部分两个相互耦合的子系统构成。电气部分包括光伏、风电、上级电网、负荷及电化学储能;氢气部分包括电解槽、储氢罐及燃料电池。其中,短时间尺度的电化学储能与长时间尺度的氢储能相配合,共同构成氢-电联合储能系统的长-短期储能协同机制。与单一的、短时间尺度的电化学储能相比,具有更好的季节性可再生能源电量消纳能力。氢-电联合储能系统结构示意图如图1所示。
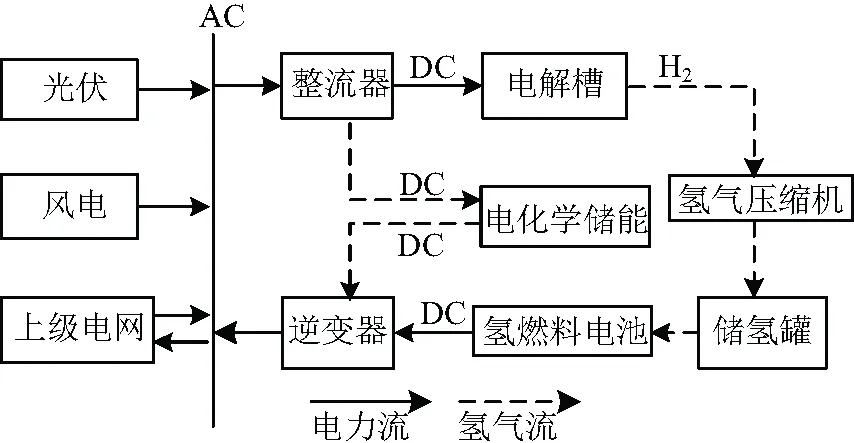
图1 氢-电联合储能系统结构示意图
1.1 电气部分建模
1.1.1 电化学储能模型
电化学储能是当前在电力系统中广泛应用的一种重要储能形式,用以调节日内短时间尺度上的电力电量平衡,保证电力系统的安全经济运行,其运行需满足各个时段内的功率约束,具体如下:
(1)

电化学储能在日内任意时段的能量约束为:
(2)

由于电化学储能的日调节特性,每天的充、放电能量应平衡,即每日的初始容量应与次日初始容量相等,具体表示为:
(3)
1.1.2 上级电网模型
上级电网具有较强的能量调节能力,协调储能平衡多余的光伏及风电出力,但受上级电网与氢-电耦合系统间电力联络线容量的限制,存在如下约束:
(4)

1.2 氢能系统建模
不同于电化学储能,氢能系统的制氢、储氢和用氢三环节可解耦运行。储氢装置存储效率高,适合季节性的长时间尺度存储;同时,可借助交通运输实现氢储能的空间转移。因此,具有广域时空尺度存储特性的氢储能逐渐受到广泛关注。本文中氢储能系统主要涉及电解槽、储氢罐及燃料电池。
1.2.1 电解槽模型
按电解质的不同,电解槽可分为碱性电解槽、质子交换膜电解槽、固体氧化物电解槽三类。碱性电解水制氢成本低、寿命长、技术成熟,目前应用较为广泛,其运行约束如下:
(5)

普通碱性电解槽冷启动时间需要数十分钟,且启停功耗较大,为避免电解槽的频繁启停,规划模型中增加如下所示的电解槽启停时间约束:
(6)
式中TO、TS分别表示电解槽允许的最小工作及启停时间。
1.2.2 燃料电池模型
现阶段广泛采用质子交换膜式燃料电池将氢能转化为电能反馈至电网,其运行约束如下:
(7)

1.2.3 储氢罐模型
储氢罐容量在一年内不同时段的约束为:
(8)

储氢罐在一年内充、放氢能量状态水平相等,可表示为:
(9)
另外,不能同时针对储氢罐进行充、放氢操作,即燃料电池和电解槽不能同时工作,有如下约束:
(10)
1.3 氢-电耦合系统的能量平衡
氢-电联合储能系统实现了电能和氢能的紧密耦合,保证了电力系统的安全稳定运行。为满足任意时段内电力系统的供需平衡(即风、光出力与负荷、各储能设备充放功率平衡),有如下约束成立:
(11)

2 长-短时间尺度氢-电混合储能规划
2.1 不确定规划方法
双层鲁棒是目前考虑风/光/荷不确定性规划的常用方法之一,常规双层鲁棒方法的上层主要以设备等年值投资成本最小为目标,以设备配置容量为优化变量;下层主要以设备运维成本最小为目标,优化变量主要为设备运行功率及运行状态。但常规双层鲁棒下层对偶问题中0/1变量的处理极其复杂,对求解器的要求很高。因此,本文在常规双层鲁棒的基础上进行改进,改进后的双层鲁棒上层目标不变,但以设备的配置容量、运行状态及运行功率为优化变量;下层以寻找造成运维成本最大时的源、荷最恶劣场景为目标,其优化变量为风、光、荷最恶劣时的0/1状态变量,两种类型的双层鲁棒优化法对比如表1所示。
改进双层鲁棒模型如式(12)所示:
(12)

将式(12)改写为如下所示的紧凑型表示:
(13)
式中x、y和z分别为待优化设备的运行功率、运行状态和规划容量,其表达式如式(14)所示:
(14)

(15)
针对上述双层鲁棒优化模型,本文采用列约束生成算法进行规划优化模型的求解[12],将原问题分解为主问题和子问题,两部分交替求解以得到原问题的最优解。主问题的具体表达式如式(16)所示:
(16)
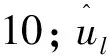
根据强对偶理论,经分解后的子问题具体表达式如式(17)所示:
(17)
式中uTλ为待规划连续变量与0/1变量的乘积,不便直接求解,根据文献[10]的结论:式(17)取最大值时,变量u为式(15)所述波动范围的边界。故,可将式(17)增加如下约束:
(18)
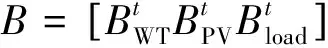
此经处理,式(17)中将出现0/1变量B与连续变量u相乘的情况,该乘积为非凸函数,需引入辅助变量及相关约束将其线性化,如式(20)所示:
(19)
根据上述公式推导和转换,双层鲁棒模型最终解耦为如式(16)所示的混合整数线性规划主问题和式(19)所示的含有对偶变量的子问题,采用采用列约束生成算法的求解流程如图2所示。

图2 改进双层鲁棒求解流程图
2.2 典型日间耦合
为降低计算量,文中通过时间序列聚类方法在一年四季中各选取一个典型日,共四个典型日参与系统规划优化运算。但因氢储能为具有年调节能力的长时间尺度储能,且储氢罐中能量必须保持连续,若直接对独立的典型日求解,则储氢罐的能量仅仅表示四个典型日的能量,不能代表全年储氢量的变化。因而,需对典型日间的耦合进行一定的处理。本文用典型日的权重系数,通过K均值聚类算法,产生四个聚类中心,同时将全年用四个典型日代替,每个典型日权重系数代表每一个季节在全年中的比重。因此,式(9)可改写为式(20)表示:
(20)
此外,为保证任意时刻的储氢罐能量状态水平均在正常范围内,即将式(10)改为式(24),该式用四个典型日表示一年8 760 h的能量状态水平,将一年8 760 h的能量状态水平限制在其允许范围之内。
(21)
3 案例分析
3.1 基本情况
根据某地区电网的源荷数据开展氢-电联合储能系统规划设计,该地区的风电、光伏及负荷容量分别为50 MW、60 MW和300 MW;上级电网与氢-电联合储能系统间电力联络线的最大允许功率为100 MW。图3是四个典型日的风/光/荷功率时序图。
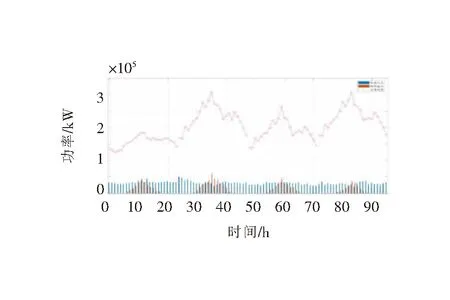
图3 风、光、荷功率时序图
设定电网在每天的0:00~8:00时段内的购售电电价为0.48元/kWh,余下时间段电价为1.35元/kWh。表2为储能系统内设备的相关参数。
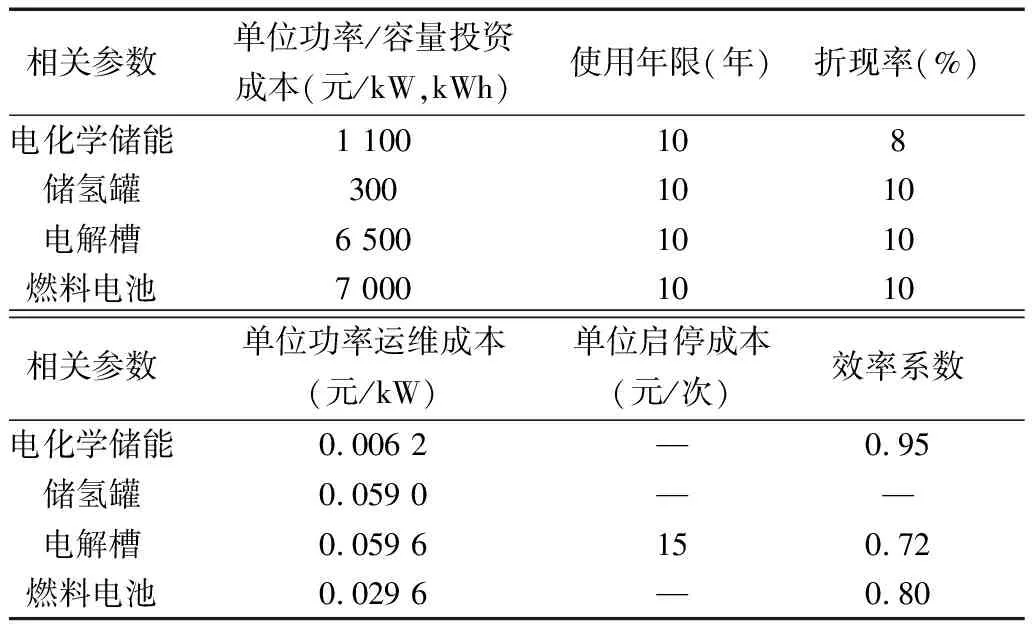
表2 储能设备相关参数表
3.2 结果分析
根据上述参数,本文基于YALMIP/CPLEX12.8的MATLAB R2018a平台开展了氢-电联合储能系统的分析计算,得到最优配置下储能设备的功率时序图,如图4~图7所示。图4和图5分别为电化学储能及氢储能一年的运行时序图,图6为储氢罐在一年不同时段的能量状态水平图,图7为氢-电联合储能系统一年内向上级电网购售电的功率时序图,各储能装置的配置功率/容量及总成本如表3所示。

表3 储能配置功率/容量及总成本汇总表
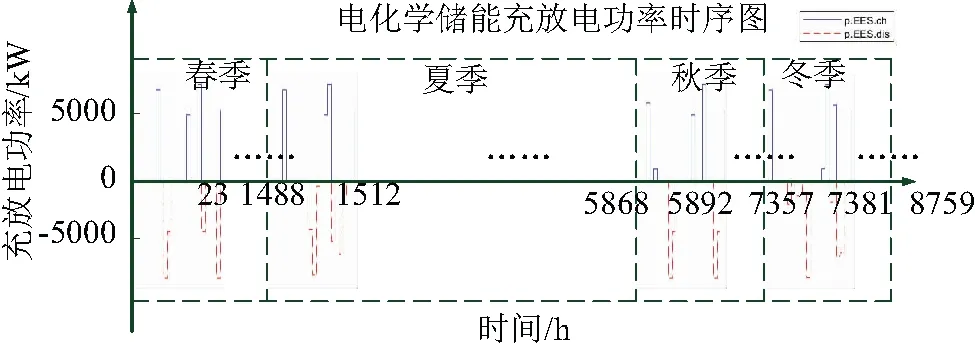
图4 充放电功率时序图

图5 充放氢功率时序图
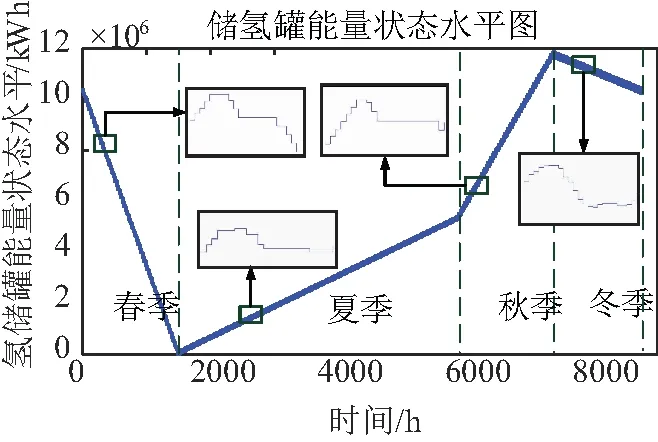
图6 储氢罐能量状态水平图

图7 购售电功率时序图
由表3可知,储氢罐作为长时间尺度的储能装置,其配置容量较短时间尺度储能的电化学储能要大得多。在此场景中,储氢罐的配置容量是电化学储能容量的1 000倍左右,且储氢罐在初始状态、电解槽在最大输出功率的情况下,可以持续充氢230小时;储氢罐在初始状态、燃料电池在最大输出功率的情况下,可以持续放氢228小时;此外,若上级电力系统的电源全部退出运行时,依靠氢储能系统仍可以维持62 h的负荷不间断供电,极大的提高了在极端灾害天气下的电网安全可靠供电。
图4为电化学储能在不同季节的典型日内充放电功率时序图。由图4可知,电化学储能在每个典型日内的充、放电能量之和为0,也即在一天内的充、放电能量是相等的;此外,电化学储能每次充、放电持续时间较短,符合本文对其短时间尺度储能的定位。
图5为氢储能在不同季节的典型日内的充放氢功率时序图,由图5可见,由于氢储能的年调节周期特性,导致每个典型日内储氢罐充、放氢功率之和不为0。而考虑典型日的占比后,储氢罐在一年内的充、放氢能量之和为0(即如图6所示),也即在一年内,储氢罐的充、放氢能量是相等的。
图6中,氢储能系统在春季和冬季释放氢气通过燃料电池转化为电能供给电网满足负荷需求,而在夏季和秋季通过电解槽电解水将电能转化为氢能储存至储氢罐中,且储氢罐年初始能量与年结束量相等。可见,氢储能系统能够维持较长时间进行充、放氢,与电化学储能构成长-短期协同储能机制。
此外,文中是将四个典型日储氢罐内的能量状态水平延伸至一年,因而被放大的四段曲线分别表示四个典型日储氢罐内的能量状态变化程度,也即分别代表了在不同季节的情况下,储氢罐内的能量状态水平变化幅度。同时也可以发现,春季典型日的能量状态水平曲线有下降趋势,延伸至一个季节后其能量状态水平曲线也有下降趋势,冬季同理;而在夏季,其能量状态水平曲线有上升趋势,秋季同理。这是由于一个典型日的能量状态水平变化幅度代表的是一个季节内每一天的能量状态水平变化幅度,且每一天的变化幅度均是一致的,因而两者有相同的变化趋势。由于每一个季节每一天充放氢的能量是不同的,因此图6中每个季节上升和下降的速率是不一致的;此外,从曲线的转折点可以清晰地看出该地区一年内夏季所占时间长,而春季、秋季和冬季三者平衡分布,其三者所占比例之和与夏季所占比例一致。
图7为该混合储能系统与上级电网的功率交互时序图。因该地区中风光出力占总源出力的35%,大部分负荷还是需要依靠上级电网的供电,因而无论在何时氢-电联合储能系统均需向上级电网购电来保证电网的稳定、可靠运行,而在各时段购得电量的多少则取决于风光出力、负荷功率、电化学储能功率、氢储能功率以及各装置的约束。
综上所述,氢储能的加入不仅提高了电力系统中的风电、光伏等可再生能源的消纳水平,与电化学储能构建了长-短期协同储能机制,既利用了电化学储能迅速充放电的优势,也结合了氢储能可实现长时间尺度电量平衡的特点。
4 结束语
季节性氢储能是当下研究的热点,如何实现长-短期储能的协同配合是目前研究的重点。在此背景下,文章构建了混合时间尺度的氢-电联合储能机制,开展了基于改进双层鲁棒方法的-电联合储能系统的不确定性规划建模,采用典型日间耦合权重针对长时间尺度内的能量平衡进行处理,提出了混合时间尺度的氢-电联合储能的规划配置方法。通过分析可知,氢储能的加入可以大大提高地区电网的风电及光伏消纳水平,与电化学储能构建了长-短期协同储能机制,既利用了电化学储能迅速充放电的优势,也结合了氢储能长时间尺度电量平衡的特点,保证了电力系统无长时能量缺失,有效提升了电力系统应对极端事件的能力。

