基于纳米压痕技术研究2024-T4铝合金力学性能

刘佳伟,郎风超*,王时雨,季宏伟,赵学平,王飞,武翔宇

(1.内蒙古工业大学 理学院,内蒙古 呼和浩特 010051;2.内蒙古工业大学 材料科学与工程学院,内蒙古 呼和浩特 010051)

材料的拉伸性能是结构设计所需的关键因素,而其对应的弹性模量、屈服应力、应变硬化率和极限拉伸强度通常通过单轴拉伸测试来测量。但对于无法制备标准拉伸试样的小尺寸构件,则需要通过其它手段获得上述材料性能。利用纳米压痕技术可以获得小尺寸试样的应力-应变(σ-ε)关系,并且与标准拉伸实验获得的相关性能一致[1],该方法利用球形压头与试样表面接触产生弹塑性变形,通过监测压入过程中载荷与压深关系而获得对应材料的σ-ε数据。

通过纳米压痕方法获得力学性能的研究主要集中于以下方面:Charles等[2]提出了压痕实验识别金属材料力学性能的反分析方法,该方法将残余压痕的最大堆积高度和力-压深数据作为反分析方法的输入参数,进而获得材料对应的弹性模量、屈服应力及应变硬化指数等。Chromik等[3]通过纳米压痕实验预测了宏观残余应力。陈冬等[4]通过纳米压痕实验得到了U-Nb合金夹杂物的硬度值、屈服强度和应变硬化指数等。Wu等[5]利用残余压痕相关数据获得了金属材料的弹塑性性能。Jordan等[6]利用纳米压痕实验和电子背散射技术相结合研究了α-Ti晶粒尺度下的弹塑性各向异性。黄礼洋等[7]通过压痕试验与有限元模拟相结合的方法,从载荷-压深曲线中获得材料的塑性性能。上述压痕实验中均采用了球形压头,因为球形压头在压痕体积内可产生相对平滑的应力/应变梯度[8]。

通过纳米压痕载荷-压深关系获得对应的σ-ε关系一直受到学者关注。Pathak等[9-12]利用纳米压痕实验获得压痕σ-ε关系,并对压痕σ-ε关系获得的压痕模量和压痕屈服强度进行了可靠性分析。Weaver等[13]通过比较Al-6061压痕σ-ε关系和单轴拉伸试验的测量数据,结果发现单轴拉伸屈服强度与压痕屈服强度之间的比例因子约为1.9。压痕σ-ε关系的方法还被推广到Ti[14-15]、立方多晶Fe-3% Si样品[16]、环氧-碳纤维复合材料[17]、聚合物-陶瓷混杂髋臼窝[18]、钢[19-22]和粘弹性材料[23]等研究中。Xiao等[24]通过压痕σ-ε关系定性研究了离子辐照材料的变形机制。Ana等[1]通过不同方法分析铁素体/马氏体P91级钢的压痕试验数据,结果表明Tabor方法[23]与几何接触半径相结合的方法获得的压痕σ-ε关系最符合P91级钢的力学性能,然后将该方法扩展到钢的高温性能预测中。Huang[25]利用有限元方法对纳米压痕实验的载荷-压深关系进行了预测,其研究表明不同定义下的应力和应变存在不确定性。

本文基于2024-T4铝合金球形纳米压痕实验数据提取所对应的压痕σ-ε关系,分析了不同压痕深度以及不同压头尺寸下的弹塑性力学性能,并与宏观拉伸实验对比确定最佳压痕参数,为利用纳米压痕研究金属材料力学性能提供实验依据。

1 材料与实验

1.1 实验材料及实验过程

利用线切割从2024-T4铝合金板材上截取10 mm×10 mm×1.5 mm方形试件,然后对试样进行打磨、抛光处理以满足压痕实验要求。采用1%HF+1.5%HCI+2.5%HNO3混合溶液腐蚀试样,在光学显微镜(Leica DM LM)上观察铝合金微观组织,如图1所示。拉伸实验在SEM配置的微型拉伸台(Kammrath Weiss Gmbh 5kN,德国)上进行,对三组试件进行单轴拉伸试验,测得其对应的极限强度、屈服强度分别为354 MPa和294 MPa,弹性模量为68 GPa,结果如图2所示。

实验中纳米压痕仪(NANO Indenter G200,Agilent,USA)所配备的球形压头半径分别为250 μm(大压头)和1.34 μm(小压头)。采用连续刚度法(CSM)方法, 利用两种不同半径压头在250、550及750nm最大压痕深度下对试样进行压痕测试,其中应变速率0.05 s-1,谐波位移2 nm,频率45 Hz,每个最大压痕深度下进行8组纳米压痕实验。

图1 2024-T4铝合金的显微组织

图2 宏观拉伸性能

1.2 理论分析

压痕实验中为了从力-压痕深度关系中获得材料所对应的σ-ε关系,Ana等[1]将几何接触半径与Hertz接触半径分别与Tabor和Pathak提出的代表性应变定义进行两两组合,产生了四种不同的将载荷-深度关系转换为压痕σ-ε关系的方法[10-11]。几何接触半径与Hertz接触半径表达形式如下[1]:

(1)

式中:ag为几何接触半径,hc为接触深度,Ri为压头半径,aH为Hertz接触半径,S为连续刚度,Eeff为有效弹性模量且满足如下关系:

(2)

式中:υs和Es分别为试样的泊松比和弹性模量,υi和Ei分别为压头的泊松比和弹性模量。

接触面积A与压痕应力σind定义如下:

A=πα2,σind=P/A

(3)

式中:α为接触半径,P为压痕载荷。

压入区域中应力与应变分布是极不均匀的,为获得单轴拉伸状态下的σ-ε关系,需采用代表性应力σ与应变ε,其对应定义如下:

σ≈σind/C*,εT≈0.2a/R,εP=4ht/(3πa)

(4)

式中:C*为限制因子,εT、εP分别为Tabor代表性应变、Pathak代表性应变,ht为压痕深度。

2 结果与讨论

2.1 载荷-压痕深度曲线

利用半径分别为250、1.34 μm的球形压头在最大压深为550 nm下得到的载荷-压痕深度曲线,如图3所示。从图中看出,纳米压痕载荷-深度曲线离散度小、重复度高,表明数据的准确性高。在最大压入深度下,半径为250 μm的压头对应荷载为325 mN,是半径为1.34 μm球形压头对应载荷的46倍,说明在相同压痕深度下,压头直径越大其所影响范围越大。卸载后大压头对应的残余压痕深度较小,弹性恢复较大,说明在加载过程中其弹性变形较大而塑性变形较小。因此,通过大直径压头可以得到相对较大的弹性变形,其对于分析材料的弹性性能具有明显优势。因此,后续研究均以大压头压痕数据为基础分析铝合金所对应的弹性力学性能,而以小压头数据分析其塑形力学性能。

图3 不同半径压头测得2024铝合金的载荷-深度曲线

2.2 刚度-压痕深度曲线

利用半径分别为250、1.34 μm的球形压头在最大压痕深度为550 nm下得到的刚度-压痕深度曲线,曲线结果为5次实验测量重复良好的平均值,如图4所示。从图4(a)中看出,曲线趋势总体分为两段,刚度随深度开始增加迅速,之后增加速度减缓并保持一定,在压痕深度为250 nm之前,刚度与压痕深度为非线性关系,在这之后基本呈线性关系,说明此时样品的弹性模量基本保持不变,压头接触部分的材料较均匀[26]。因此,在通过大压头获得样品的弹性模量时应取压深为250 nm之后的数据进行研究分析。从图4(b)中看出,当压痕深度小于20 nm时,实验数据受金刚石压头钝化、机械分辨率等因素影响具有很大的误差。因此,为了更好地分析弹性模量随压痕深度的变化,压痕深度必须大于20 nm[27]。

图4 刚度-深度曲线

2.3 弹性模量和硬度

压头半径为250 μm且最大压痕深度为550 nm时,连续测得弹性模量E和硬度H与深度关系曲线,如图5所示。压痕深度在20 nm以内测得的弹性模量和硬度并不可靠,之后弹性模量和硬度值随压痕深度的增加而增大,并在压痕深度为250 nm之后趋于稳定,将其基本保持不变阶段的平均值认为是试样的弹性模量和硬度。

图5 弹性模量和硬度与深度曲线

图6 不同压头半径情况下的弹性模量和硬度与最大压痕深度的关系

半径为250和1.34 μm压头测得弹性模量和硬度与不同最大压痕深度(hmax=250、550、750 nm)的关系,如图6所示。大压头在最大压痕深度为550 nm时测得平均弹性模量为66.4 GPa,与宏观拉伸弹性模量的误差为2.3%,最接近宏观拉伸弹性模量值,而小压头的平均弹性模量值稳定在82.3 GPa左右,高于宏观拉伸弹性模量约21%。因此,大压头在最大压痕深度为550 nm下能够更好的评估宏观拉伸弹性模量,且此时测的硬度值为0.7 GPa并趋于稳定。注意到,小压头与大压头测定的弹性模量和硬度值随最大压痕深度的变化趋势不同,并且小压头的测定值均明显高于大压头的测定值,这主要是尺寸效应的影响。球形压痕的尺寸效应主要表现为压头越小,球形压痕下方的局部应变梯度越大,硬度越大[28]。在图6(a)中,随着压痕深度的增加,应变梯度增加,使大压头的硬度有所增加,但是压头尺寸对硬度的影响更加显著。压痕弹性模量与压痕下积累的损伤[29]有关,随着压痕深度的增加,位错在晶界、第二相等障碍物处不断堆积进而形成空隙,造成损伤。弹性模量先因刚度的增加而增加,之后损伤占主要作用,随着损伤的积累而减小,所以大压头测的弹性模量更接近宏观拉伸弹性模量。在图6(b)中,由于小压头尺寸太小,压痕下几乎没有损伤积累,尺寸效应比压痕深度的影响更加显著,所以测得的弹性模量和硬度更趋近材料的理想值。在压入深度为550 nm时,小压头测得数据发生较为明显的离散,主要由材料表面粗糙度等因素引起。

2.4 应力-应变关系验证

图7显示了在压头半径为1.34 μm、最大压痕深度为250 nm下,将几何接触半径和Hertz接触半径分别应用于Tabor和Pathak应变公式而获得的平均σ-ε关系。从图7(b)中可看出,采用Hertz接触半径模型时,σ-ε关系产生了明显差异,这是因为接触刚度随深度变化的准确性对计算结果有很大影响。在恒定的应变率下,随着压痕实验的进行,作用力速率呈指数增加[30]。因此,采用几何接触半径与Tabor和Pathak应变公式相结合的方法,更适合在2024-T4铝合金材料上获得σ-ε关系。

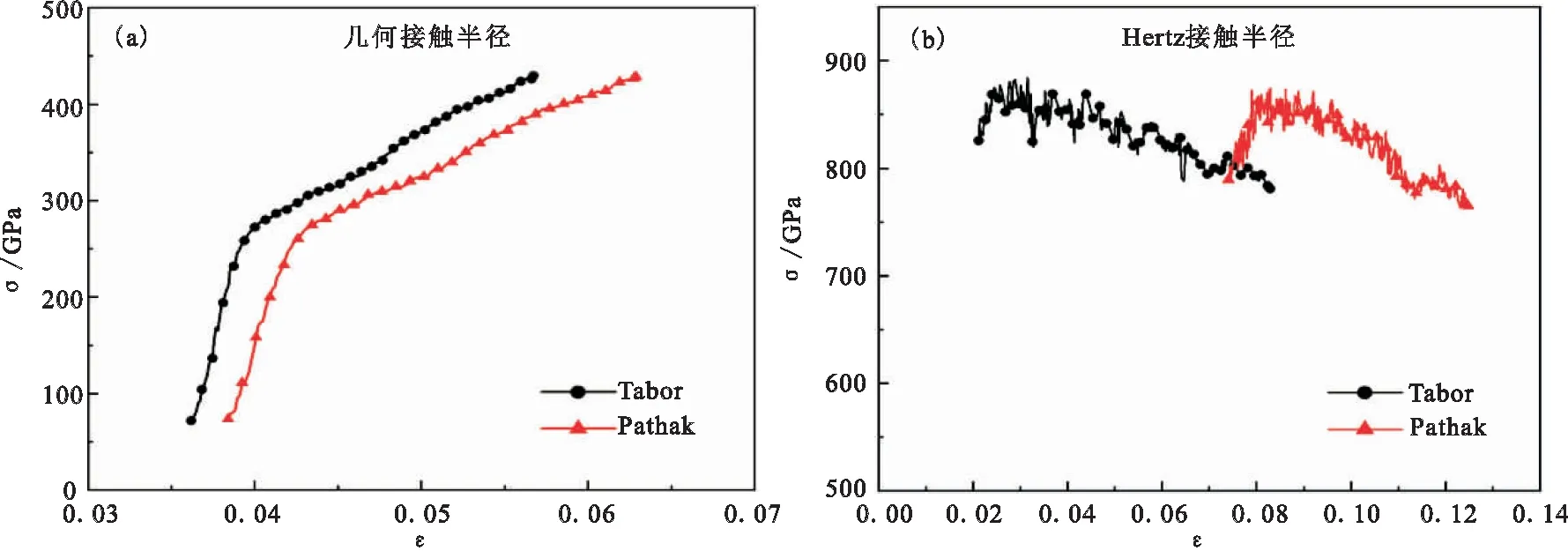
图7 不同接触半径应用于Tabor和Pathak应变公式而得到的压痕σ-ε曲线

仅采用几何接触半径和Tabor应变公式相结合的方法,从压痕σ-ε关系中提取压痕拉伸性能,结果如图8所示。得到的弹性模量E为70 GPa,与宏观拉伸弹性模量的误差为3%,0.2%应变偏置的压痕屈服强度σy为290 MPa,与宏观拉伸屈服强度的误差为1.4%,计算结果可靠。此时采用的限制因子C*为1.6(见式4),不同于Tabor(C*=2.8)[31]、Patel(C*=2.2)[32]和Weaver(C*=1.9)[13]等研究者提出的限制因子,而且该类型的限制因子往往会受接触半径计算方法和材料本身的影响。因此,采用限制因子C*为1.6作为应力转换系数不仅可以明显简化分析,还能较为准确的表征2024-T4铝合金样品的弹塑性力学性能。为充分发挥CSM测量模式的优势,对影响纳米压痕测量的材料表面质量、压头尺寸[33]以及适用的可靠数学关系[34]仍需要进一步研究优化。

图8 基于几何的接触半径应用于Tabor应变公式得到的压痕σ-ε曲线

3 结 论

(1)小压头(1.34 μm)测得的弹性模量和硬度值均高于大压头(250 μm)的测定结果,表现出明显的压痕尺寸效应。

(2)采用几何接触半径与Tabor和Pathak应变公式相结合的方法,均可在2024-T4铝合金材料上得到良好的σ-ε关系。

(3)采用限制因子C*为1.6作为应力转换系数,从压痕σ-ε关系中得到弹性模量为70 GPa,与宏观拉伸弹性模量的误差为3%,0.2%应变偏置的压痕屈服强度σy为290 MPa,与宏观拉伸屈服强度的误差为1.4%,较为准确的表征了2024-T4铝合金样品的弹塑性力学性能。