稳态法测量固体的导热系数实验与分析*

范淑媛 罗裕波

华中科技大学材料科学与工程学院 武汉 430074

0 引言

热传导是热量传递的三种基本形式之一，是指物体各部分之间不发生相对宏观位移情况下由于温差引起的热量的传递过程，其微观机制是热量的传递依靠原子、分子围绕平衡位置的振动以及自由电子的迁移。在金属中，自由电子起支配作用，在绝缘体和大部分半导体中则以晶格振动起主导作用。一般说来，金属的导热系数比非金属的要大；固体的导热系数比液体的要大；气体的导热系数最小。因此，某种物体的导热系数不仅与构成物体的物质种类密切相关，而且还与它的微观结构、温度、压力、湿度及杂质含量相关。

导热系数是表征材料热传导能力大小的物理量[1]，在科学实验和工程设计中，需要了解所用物体的一些热物理性质，导热系数就是重要指标之一，常常需要用实验的方法来精确测定。测量导热系数的方法很多，没有哪一种测量方法适用于所有的情形，对于特定的应用场合，也并非所有方法都能适用。要得到准确的测量值，必须基于物体的导热系数范围和样品特征，选择正确的测量方法。测量方法可以分为稳态法和非稳态法两大类[2]。稳态法是在加热和散热达到平衡状态、样品内部形成稳定温度分布的条件下进行测量的方法[3]。非稳态法则是在测量过程中样品内部的温度分布是随时间变化的，测出这种变化，得到热扩散率再利用物体已知的密度和比热，求得导热系数[4]。

本实验装置是采用稳态法测量固体的导热系数的一种设计方案，学生通过该实验，理解掌握本稳态法实验装置的工作原理和实验方案；利用该装置测量不同材料的导热系数以及同种材料不同厚度试样的导热系数，并将试样的参考值进行比较，分析实验装置的可靠性、影响测量结果的影响因素等。

1 实验装置

本实验装置原理如图1 所示，上端为加热源，可以设置系统上端加热温度；上下压杆为导热良好的纯铜材料；待测试样放在上下压杆之间，在上下铜压杆的中心轴不同位置处放置4 个温度传感器，分别用T1、T2、T3、T4标识，T1、T2间距和T3、T4间距均为h1，T2到上压杆下表面的间距和T3到下压杆上表面的间距均为h2；整个装置放置在抽真空环境下，下压杆的下表面和冷水装置相连。

设备工作时，加热器不断将热量传到上压杆，上压杆将热量传到待测试样，试样热量传到下压杆，下压杆的下表面和冷却箱中的恒温水相连通，热量最后由冷却水带走。

2 实验测量原理

当系统热传导达到平衡状态时，T1、T2、T3、T4的值将保持不变。由于整个装置放置在抽真空环境下，所以不用考虑系统侧边横向空气中对流散热，那么在系统达到稳态时，加热器单位时间内传给上压杆上表面的热量等于下压杆下表面冷却水带走的热量，也就是说达到稳态时，上下压杆、试样任意横界面单位时间流过的热量都相等。

根据傅里叶热传导定律[5-6]有：

其中，Q样为单位时间内通过试样的热流量；λ样即为试样的导热系数（又称作热导率）；S为试样传热的有效导热面积，如果S样＜S铜，那么系统的有效传热面积为S=S样，本实验中选择试样的面积S样等于或略大于压杆的横截面S铜，那么系统的有效传热面积为S=S铜；T上和T下分别表示试样的上、下表面的温度，其分别等于上压杆下表面的温度和下压杆上表面的温度，故可以通过铜上下压杆的温度变化梯度来求得，如式（3）、式（4）；d为试样的厚度。

由于系统处于稳态条件下，理论上来说，单位时间内通过试样以及上下压杆任意横截面的热流量是相同的，即Q样的值也等于单位时间内通过上下压杆的热流量Q铜。

在实验中，考虑到测量误差，Q铜通常取上下压杆在单位时间通过的热流量的平均值，如表达式（2）：

试样上下表面的温度T上和T下可以通过式（3）、式（4）求得：

故由（1）式可以得到：

因此，稳态条件下，分别读取T1、T2、T3、T4的值，就可以计算出试样的导热系数λ样的值。

3 实验数据记录和处理

实验设备基本参数：h1=50 mm，h2=2 mm，S铜=706.858 mm2，λ铜=380 W·m-1·K-1；实验系统的热端温度最高可加热到70 ℃，主要热交换系统放置在真空度为0.1 MPa 的腔体内；试样分别为厚度为0.796 mm 和1.695 mm 有机玻璃以及厚度为2.065 mm石英玻璃，0 ～100 ℃有机玻璃的导热系数参考值为0.19 W·m-1·K-1，50 ℃左右时石英玻璃的导热系数参考值为1.35 W·m-1·K-1；实验时为了减小接触热阻需要将样品上下表面涂上导热硅胶，其导热系数为2.0 W·m-1·K-1。

实验方法：安装好待测样品，设定好热端加热的温度值，设置系统稳态条件为：60 秒内，T1、T4和T2、T3的差值变化不超5%。系统开始工作，并将不断自动识别T1、T2、T3、T4的变化情况，待系统达到符合稳态条件时，分别记录T1、T2、T3、T4的值，可以求得该试样在该状态下平均温度的导热系数。

3.1 相同条件下测量试样的导热系数

将仪器热端加热的温度值设置为40 ℃，测量了厚度为0.796 mm 和1.695 mm 有机玻璃的导热系数以及厚度为2.065 mm 的石英玻璃的导热系数，实验结果如表1、表2、表3 所示。

表1 厚度为0.796 mm 的有机玻璃实验数据记录和处理结果

表2 厚度为1.695 mm 的有机玻璃实验数据记录和处理结果

表3 厚度为2.065 mm 的石英玻璃实验数据记录和处理结果

实验结果表明同一试样反复测量，数据重复性非常好，且与参考值比较，误差都比较小，说明将热传导装置放在真空条件下，控制系统不向侧边对流散热，简化了系统模型，提高了实验精度，表明该实验方法设计科学合理。

但是在测量不同厚度的有机玻璃时，发现同样的条件下，厚度为0.796 mm 和1.695 mm 有机玻璃的导热系数有明显差异，薄的试样测量导热系数明显比厚的要大，理论上导热系数的值和试样的厚度无关[7]，如果考虑到侧面散热的问题，那么试样的厚度越薄越好[8]，因为如果样品的厚度过大，抽真空度不太高的情况下，边侧的散热不可忽略，故厚的试样的测量结果更容易偏大，与本实验结果不符。经过分析，发现在试样表面涂导热硅胶时，硅胶有少量溢出也会从上表面经侧壁流动到下表面，这样会使得测量的导热系数偏大；实验条件相同时，从表1 和表2 中可以发现薄的材料的温度平均值会高于厚的材料，这也是造成薄的材料导热系数的测量结果大于厚的材料的原因。

3.2 不同温度下测量试样的导热系数

将实验系统的热端温度分别设置为40 ℃、45 ℃、50 ℃、55 ℃、60 ℃、65 ℃时，分别测量有机玻璃和石英玻璃的导热系数。待系统达到稳态并分别记录T1、T2、T3、T4的值，可以求得试样分别在相应的平均温度下的导热系数值，并用实验结果中的平均温度和测得相应试样的导热系数作图，如图2、图3 所示。

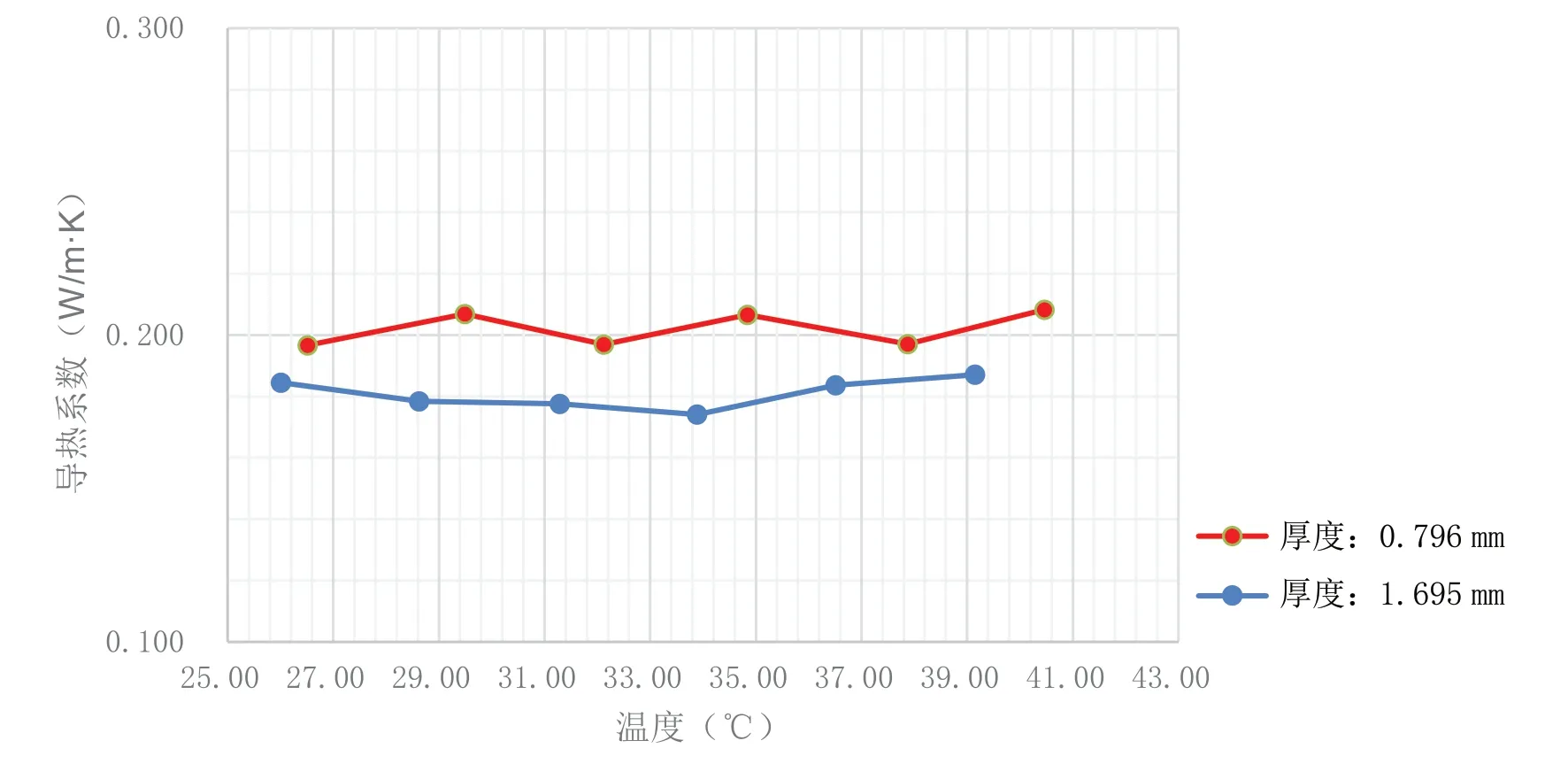
图2 不同厚度有机玻璃的导热系数和温度的关系

实验结果表明，样品的平均温度在25 ～41 ℃区间内，测得有机玻璃和石英玻璃的导热系数与参考值比较，值都在合理范围内且误差比较小；随着温度的升高，石英玻璃的导热系数有较明显的上升趋势（如图3 所示），这与材料的特性相符。系统升温过程中，平均温度在25 ～41 ℃区间内，较薄的有机玻璃的导热系数普遍比较厚的大（如图2 所示），分析原因，可能是有少量的硅胶从上表面溢出经侧壁流动到下表面。

4 结束语

测量了有机玻璃和石英玻璃的不同厚度试样的导热系数，实验设定稳态条件为温度变化值在5%内保持1 分钟，每个样品的测试时间约为25 分钟。对实验结果进行对比分析，发现对低导热材料而言，稳态热流抽真空法实验方案具有准确度高、重复性好、测试原理简单等特点。该实验适合作为本科生实验开设。

为了有更好的实验精度，实验时，需要在试样的上下表面涂上导热硅胶，在上下压杆压紧试样后，要稳定一定时间，再将从边沿溢出的硅胶擦除干净，否则会使实验结果偏大；本实验的上下压杆的直径为30 mm，试样的厚度在1 ～3 mm 为佳；试样的面积要等于或略大于上下压杆的面积，且安装试样时，要将试样的边缘和压杆的边缘对齐，否则也会导致实验误差；利用该实验装置，由于传热系统在真空条件下，没有向侧面散热，同样实验条件下，会有薄的试样的平均温度高于厚的试样，故会导致薄的试样的导热系数测量值大于厚的试样。

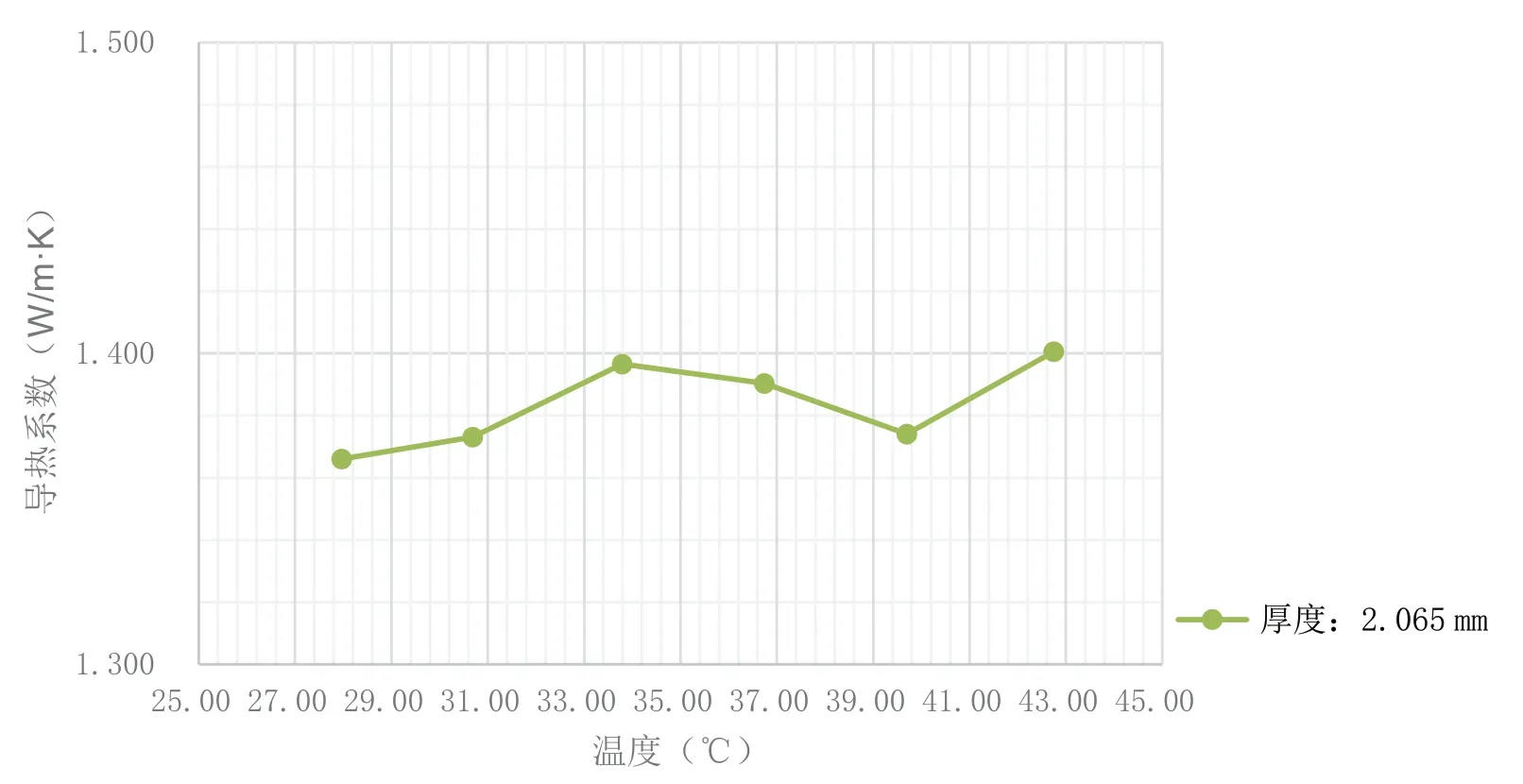
图3 石英玻璃的导热系数和温度的关系