核电厂考虑结构参数不确定的地震易损性分析

秦苗珺, 赵衍刚,2, 卢朝辉

(1. 北京工业大学 城市建设学部, 北京 100124; 2. 神奈川大学 工学部建筑学科, 日本 横滨 221-0806)

0 引言

核电厂发生事故后,对社会和环境将产生难以估量的影响,因此,核电厂的安全运营是关乎经济发展与社会安定的根本。核电站设计建造过程中应考虑各种不确定因素对其安全性的影响,并针对这些因素采取相应有效的措施。自从福岛核事故以来,越来越多的研究人员对既有核电站和新建核电站重新进行安全评估。由于同一震级下不同结构的地震烈度有明显区别,不同的烈度主要取决于建筑的结构材料,施工质量等因素,其中结构的材料属性可反映施工质量的优劣,影响着结构的整体性能。因此,材料参数不确定性对结构抗震性能的影响仍不可忽略。

在核电厂的抗震分析中,对核电站在超过基准地震动作用下的有效评估是保证核电安全的关键。因此,核电站的地震概率风险评估(Seismic Probability Risk Assessment,SPRA)已广泛应用于新建或已建的核电站系统的安全评估中[1]。而地震易损性分析是SPRA中至关重要的部分,是评估在地震作用下结构可靠性的关键步骤,为抗震设计与风险评估提供指导依据。因此,准确获得结构的易损性是地震风险评估的前提条件。目前,美国所提出的多种地震易损性分析方法已被世界许多国家所采用[2],主要为以下三种方法:Zion法[3]、地震安全裕度法(Seismic Safety Margin Research Program,SSMRP)[4]和BNL(Brookhaven National Laboratory)[5]方法。其中Zion法与SSMRP法都通过专家评估与经验判断确定,结果具有较大的主观性。在BNL方法中,通过随机振动理论与极值理论获得结构的最大反应分布,而参数不确定则是通过拉丁超立方抽样进行考虑。Whittaker等[6]综述了隔震核电厂地震易损性的发展。Zhao 等[7]对屏蔽厂房进行了地震易损性评估,考虑了流固耦合对其影响,同时采用三种不同方法建立了核电厂系统的易损性曲线。

在实际工程结构中除地震动激励的不确定外,还存在外部环境、材料属性和人工干预等不确定因素,而多数核电厂的风险评估中未考虑参数不确定的影响[8]。研究表明,参数不确定对结构可靠性分析有不利的影响[9]。早期是通过蒙特卡洛模拟(Monte Carlos Simulation,MCS)[10]考虑参数不确定,但由于模拟方法对于小失效概率事件计算量庞大,并且获得结构的响应函数计算时间成本较大,难以直接使用。随后许多学者针对该方法进行了改进,发展了不同的抽样方法,N Yun等[11]提出采用一组模型的输入输出样本估计整体可靠性灵敏度指标的方法,并结合子集模拟以减小计算量;Alvarez等[12]采用随机集理论计算失效概率的上下界,其中变量之间的相关性采用Copula函数表示,该方法对于低维空间有较好的适用性。Alban等[13]提出了一种高效处理高维、小失效概率问题的子集模拟方法,选择合理的中间失效事件,将较小的失效概率表达为一系列较大失效概率的乘积,并利用马尔科夫链模拟(Markov Chain Monte Carlo,MCMC)方法生成条件样本计算失效概率,该方法对变量维数、极限方程形式等均没有限制,适用于非线性较高的小失效概率可靠性问题,但对于中间失效事件的选取及生成样本的相关性对计算结果有较大的影响,为减小其影响,发展了自适应重要抽样法等[14-15]。其次以展开法为主的矩法等是考虑参数不确定的有效方法[16]。Zhao Y G等[17]提出高阶矩方法,对已有方法进行了简化,同时具有较高的精度。一次二阶矩法(First-Order Second-Moment,FOSM)与MCS方法相比因计算简单已被广泛应用于各种结构,如混合结构、钢结构、桥梁结构的易损性分析中[18-19]。蒋亦庞等[20]基于FOSM方法分析了无筋砌体结构在参数不确定下的地震易损性,结果表明,参数不确定对易损性的影响不可忽略。

本文以混凝土的材性参数为随机变量,采用ANSYS有限元建模,通过与试验结果对比验证,表明有限元模型可作为易损性分析中的模拟工具。在此基础上结合增量动力法(Incremental Dynamic Analysis,IDA)[21]与FOSM考虑核电厂在参数不确定下的地震易损性,得到核电结构的地震易损性曲线。结果表明,参数不确定对核电结构的地震易损性具有显著的影响。

1 核电厂结构模型与验证

1.1 核电站的有限元模型

本文利用有限元软件ANSYS的交互仿真平台,对CAP1400核岛结构及周边附属厂房建模。其尺寸如图1所示。本文主要考查核岛结构在地震作用下结构关键点的动力响应,因此在建模时对实际的复杂结构进行适当的简化,不考虑屏蔽厂房内部钢制安全壳的影响。因结构的厚度方向尺寸相对较小,屏蔽厂房和辅助厂房采用壳单元,选用SHELL181薄壳单元进行建模,基础底板采用实体SOLID65单元。保证混凝土材料全曲线有下降段,本文采用了多线性随动强化(MKIN)模型考虑混凝土进入塑性的性能(图2)。为满足规范要求,采用C50混凝土,抗压强度fc=23.1 MPa,密度rc=2 500 kg/m3,弹性模量Ec=3.45×104MPa,泊松比uc=0.18。混凝土的应力应变曲线采用Kent-Park模型[22]。屏蔽厂房和辅助厂房之间、结构和土体之间采用MPC型绑定约束。场地岩土力学参数如下:rs=2 600 kg/m3,Es=10 030 MPa,剪切波速vs=1 250 m/s,泊松比us=0.32,内聚力cs=0.9 MPa,摩擦角fs=42.8°,选用ANSYS中自带的Drucker-Prager模型。土体周围边界参考刘晶波等[23]和Deeks等[24-25]提出的黏弹性人工边界,如图3所示。其中,弹簧阻尼器单元的参数按式(1)和式(2)确定。

图1 核电站结构模型平面图(单位:mm)Fig.1 Plan of the nuclear power plant structure model (Unit:mm)

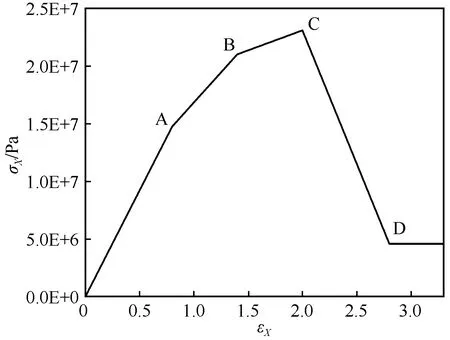
图2 混凝土线性随动强化模型Fig.2 Linear kinematic hardening model of concrete

图3 三维黏弹性人工边界示意图Fig.3 Diagram of the 3D viscous-elastic artificial boundary

法向:

(1)

切向:

(2)

根据以上结构参数建立的核岛结构有限元模型如图4所示。

图4 核电站的整体模型Fig.4 Overall model of the nuclear power plant

1.2 模型验证及对比

为验证有限元模型的准确性,建立与振动台试验相一致的模型进行对比。试验模型采用1∶40缩尺比例,缩尺后的模型尺寸为2 285 mm×1 058 mm×1 188mm(长×宽×高),屏蔽厂房尺寸1 200 mm×2 194mm(直径×高),底板厚160 mm。附属厂房和屏蔽厂房部分模型如图5所示。地震动输入选用安县地震记录。安县地震动是2008年汶川地震中观测到的地震加速度记录[26],其中水平X方向的峰值加速度为2.99 m/s2,持续时间为50 s,时间步长为0.008 s。地震动加速度时程如图6所示,相应的加速度反应谱如图7所示。峰值加速度采用0.3g。选取屏蔽厂房沿标高从上到下7个关键点进行对比。图8展示了安县地震动下个测点峰值加速度的试验结果与有限元分析结果的对比。

图5 核电站试验的缩尺模型与振动台试验的 整体模型Fig.5 Scale model of the nuclear power plant and overall model of shaking table test

图6 输入的地震动及加速度时程Fig.6 Input ground motions and acceleration time history

图8 安县地震动下各测点峰值加速度的试验结果与有限元分析结果的对比Fig.8 Comparison between test result and finite element analysis result of peak acceleration of each measuring point under Anxian ground motion

从图8中可看出,有限元模型在一定程度上反映了结构的真实动力特性。从X方向可看出,振动台试验中,核岛结构下部加速度响应较有限元结果偏小,数值模型的整体加速度响应从底部到顶部变化范围小,有限元模型沿高度方向基本呈线性变化,表明结构处于弹性状态,整体刚度比试验模型偏大;结构顶部的峰值加速度比有限元模型的偏大,其主要原因可能是X方向的结构刚度沿层高分布不均匀,同时在试验中土体属性由于振动过程有所改变,与结构之间的接触边界也相应发生变化。而Y、Z向峰值加速度的数值分析结果与试验相比偏大,可能由于模型中两方向的整体刚度较大的原因,试验中土体的整体刚度未达到预期效果,而且由于土层在振动台试验过程中整体形态有所变化,与结构之间的相互作用减弱。因此,在软弱地基下造成结构响应偏小。从上图表明该有限元模型在一定程度上可等效为实际的核电厂结构。

通过将上述缩尺模型按照相应比例放大为原模型尺度,场地土采用相同的土体参数,人工边界采用同样的黏弹性人工边界,并利用该模型进行易损性分析。

2 地震动参数及结构极限状态

2.1 地震动与地震强度指标选取

通过已有研究表明,在IDA中选取20条地震记录足以考虑地震动输入的不确定性[4,9]。本文依据AP1000反应谱(图9)从美国太平洋地震研究中心PEER的强震数据库中选取20条实测地震记录,震级分布在5.2～7.49,峰值加速度分布在0.08g～0.76g,如表1所列。

表1 20条天然地震动记录

图9 AP1000设计反应谱Fig.9 Design response spectrum of AP1000

地震易损性分析中常用的地震动强度参数(Intensity Measure,IM)一般取为结构基本周期对应的加速度谱值Sa(T1,5%)(T1为结构的基本周期)或峰值加速度 (Peak Ground Acceleration,PGA)。由于结构参数不确定会导致结构基本周期成为一个不确定变量,采用Sa(T1,5%)作为IM参数会使分析变得复杂,因此,选取PGA作为IM参数。在进行IDA分析时,分别将20条地震记录的PGA调整为0.05g～0.8g(间隔为0.05g),对结构进行有限元分析。

2.2 核电结构不确定参数

由于核岛结构以混凝土材料为主,因此选用混凝土的密度rc,弹性模量Ec,泊松比uc,抗拉强度ft作为随机变量。由于目前针对核电结构不确定性参数之间的相关性研究仍不充分,现有文献难以获得参数间的相关系数,因此本文采用简化分析处理,假设各参数之间相互独立。同时,本文也不考虑模型参数在结构空间分布上的不确定性,假设四个随机变量的概率信息如表2所列。

表2 结构不确定性参数的概率信息

2.3 结构极限状态的定义

本文参考了Crowley等[27]提出的基于失效模式反演结构在不同极限状态的抗震能力的方法,通过基于变形与应力混合控制的方法定义极限状态,假设结构的最大拉应变达到混凝土的极限拉应变作为结构轻微破坏的极限状态(Limit State,LS)LS1;中等破坏为LS2,定义为混凝土最大压应变达到极限压应变的一半;严重破坏定义为混凝土达到峰值压应力所对应的极限状态LS3。

文中选取屏蔽厂房结构的顶部位移作为结构抗震性能指标,通过PUSHOVER分析确定核岛结构的三个极限状态对应的顶部最大位移,如表3所列。

表3 顶部最大位移限值

3 考虑结构参数不确定性的地震易损性分析方法

3.1 地震易损性模型

结构地震易损性是指在不同强度的地震作用下,结构超过某一特定极限状态的失效概率,从宏观上反映了地震动强度与结构的损伤程度之间的关系,是评估结构抗震性能水平的关键组成部分。通常结构的地震易损性计算模型可表达为在某一确定的地震强度IM下,地震需求D达到或超过结构抗震能力C的条件概率,即,

FG(x)=P[D≥C|IM=x]

(3)

式中:FG(x)为易损性函数,通常采用对数正态分布作为易损性概率模型[28-29],即认为地震需求D与抗震能力C均服从对数正态分布,对于某一特定极限状态LS,地震易损性可表示为:

FG(x)=P[LS|IM=x]=

(4)

式中:Φ[·]是标准正态变量的累积分布函数;Ci为极限状态LSi下结构抗震能力限值;mG与βG分别为结构地震易损性函数的中位值和对数标准差。当不考虑参数不确定时,βG=βRTR,表征仅有地震动不确定性的影响,可根据16%分位曲线与84%分位曲线,按照式(5)计算得到[30]:

mR,16%=mGexp(-βRTR)
mR,84%=mGexp(βRTR)

(5)

式中:mR,16%表示16%分位曲线;mR,84%表示84%分位曲线。

通过式(5)可得到相应的地震易损性曲线。地震易损性曲线直观反映了结构的抗震性能,曲线的中心点取决于结构的抗震极限承载能力,而其形状主要由结构抗震性能的不确定决定,如图10所示。当结构参数不确定性较大时,不考虑不确定性所带来的影响容易高估结构的可靠性,使得结构偏于不安全。因此,在参数不确定的条件下,有必要结构参数对结构地震易损性的影响。

图10 地震易损性曲线的概率特征Fig.10 Probability characteristics of seismic fragility curve

3.2 基于FOSM-IDA考虑参数不确定的易损性分析方法

本文采用FOSM考虑参数不确定的影响。假设结构存在随机变量X=[X1,X2,…,Xn],诸如结构材料的弹性模量,强度等。易损性函数如式(4)中,由于参数不确定的影响,mG与βG均体现为随机变量的形式,即考虑参数不确定的易损性模型转化为对模型参数的估计,以下将通过FOSM确定对数均值mG与对数标准差βG。

假设结构的功能函数Z为随机变量X的函数Z=G(X),FOSM方法是通过将函数在随机变量X的均值μX处近似展开为一阶泰勒级数形式估计相应的均值和方差[19],如式(6)和式(7)所示:

μZ≈G(μX)

(6)

(7)

(8)

当随机变量相互独立时,式(7)可写为:

(9)

据文献[31]通过数值模型与式(9)即可得到各随机变量在各个取值(即平均值加减一倍标准差)下的地震需求与参数不确定下的对数标准差。综合考虑地震动不确定和结构参数不确定后,此时新定义的易损性函数的总对数标准差βTOT如式(10)所示:

(10)

式中:βRTR与βMOL分别表示只考虑地震动不确定与结构参数不确定的对数标准差,可分别根据式(5)和式(9)计算得到。

4 核电结构易损性分析结果

选用20条实际地震动记录作为输入(表1),对核电站结构进行IDA分析,并按照上述方法考虑不确定参数下的地震易损性分析,得到各峰值加速度下不同地震记录的结构最大响应值,通过采用基于IM准则得到16%、50%和84%分位数曲线如图11所示。

图11 16%、50%和84%分位数曲线Fig.11 16%, 50%, 84% quantile curves

由图11可知,以上三条分位数曲线在起始阶段有明显的线弹性段,表明结构响应与PGA是线性关系,随着PGA的增加,曲线斜率明显减小,结构响应出现非线性。

通过对IDA结果进行统计回归后,得到未考虑结构参数不确定的地震易损性曲线,同时基于FOSM计算结构参数不确定下核电结构不同极限状态的地震易损性曲线,如图12所示。其中NON-表示只考虑地震动不确定时的计算结果,CON-表示同时考虑地震动和结构参数不确定性时的计算结果。

图12 结构易损性曲线的对比Fig.12 Comparison between structural fragility curves

根据地震易损性曲线的特性可知,曲线的倾斜程度反映了不确定性对地震易损性的影响程度。当PGA处于0.7g～1.4g时,达到LS2极限状态的失效概率在0.2～0.8范围内,表明结构响应存在较大的离散性,并且在LS3极限状态表现更加明显。通过图12可看出考虑参数不确定与未考虑参数不确定的两条易损性曲线不重合,考虑参数不确定的易损性曲线斜率小于未考虑参数不确定的易损性曲线,未达到地震强度中位值前,考虑参数不确定后计算失效概率高于未考虑参数不确定的情况,并且随着破坏等级提高,其相差越大。当在LS2破坏等级,考虑地震动输入不确定与参数不确定的对数标准差分别为βRTR=0.235和βMOL=0.174(表4),两者比值βMOL/βRTR为0.738。可见,结构材料参数不确定对核电站厂房结构的地震易损性的影响不能忽略。

表4 结构参数不确定对地震易损性的影响

为进一步研究以上四个随机变量对核电结构的地震易损性的影响,对不确定参数进行敏感性分析。在上述计算的基础上,随机参数分别取均值增减1倍和2倍标准差进行地震易损性分析。此时,每个参数下包括5个计算工况:μXi,μXi±σXi,μXi±2σXi。以易损性曲线的地震强度中位值mR作为评价指标,对每个结构参数下的5个计算工况结果进行归一化处理:

(11)

结果如图13所示。从图中可看出,除弹性模量外,其他参数均在0.87～1.08范围内变化,变化幅度为0.21。而弹性模量的归一化结果的变化范围是0.76～1.23,幅度为0.46,是前者的两倍之多。表明材料弹性模量的敏感性远高于其他三个参数,是结构地震易损性分析的控制性参数。

图13 地震强度中位值随各结构材料参数的变化规律Fig.13 Variation of the median value of seismic intensity with different structural material parameters

5 结 论

以核电站厂房为研究对象,采用IDA方法计算地震易损性,并基于FOSM考虑结构材料参数的不确定对其影响,主要结论如下:

(1) 在核电厂结构地震易损性分析中,需要同时考虑地震动与结构材料参数两类不确定的影响,并且随着破坏等级的提高,结构不确定性参数UI易损性的影响程度也越大。

(2) 结构参数的不确定相比于地震动不确定是不可忽略的,结构参数不确定的标准差占到地震动不确定标准差的60%,因此有必要在核电站易损性分析中同时考虑两种不确定的影响,同时,在核电站的四种不确定参数中,以弹性模量对地震易损性的影响最为显著,是参数不确定中的控制因素。

(3) FOSM-IDA便于计算,可作为工程中一种计算地震易损性的有效方法,通过考虑参数不确定的影响,能够有效解决原有方法在低失效概率情况下高估结构抗震性能的问题,更加准确地评估结构的易损性。