考虑阻尼器极限状态的耗能减震体系斜拉桥抗震性能分析

陈 晨, 刘金龙, 林均岐

(1. 中国地震局工程力学研究所 地震工程与工程振动重点实验室, 黑龙江 哈尔滨 150080;2. 地震灾害防治应急管理部重点实验室, 黑龙江 哈尔滨 150080)

0 引言

近几十年来,斜拉桥以跨越能力卓越、造型美观、能充分利用材料性能等优点,已广泛运用于各国桥梁建设中。斜拉桥大多是路网中重要的交通枢纽,其固有阻尼较小,基频较低,对地震作用较为敏感[1],斜拉桥的震害往往会造成整个路网服务能力的剧烈下降。因此,在对斜拉桥进行设计时,很重要的一个课题就是如何减小其地震反应,以确保结构在地震作用下的安全。当前,基于被动控制理论的桥梁减震策略在实际工程中得到了广泛应用,其是通过对结构附加被动耗能装置来提高结构的抗震性能[2-4]。其中在斜拉桥抗震设计中应用最广的就是黏滞阻尼器,因其不影响结构周期、耗能能力强等优点,使其具有良好的减震效果,如上海东海大桥[5]、江苏苏通大桥[6]、芜湖长江公路二桥[7]等。

通常情况下,在研究这些耗能减震设计斜拉桥的抗震性能时是不需要考虑黏滞阻尼器自身发生破坏的,而是将研究的重点集中在阻尼器的参数优化上[5-6,8-11]。阻尼器满足规范中的相关规定,在设防地震作用下正常工作即可。我国《建筑抗震设计规范》[12]对速度相关型消能器做出了规定,要求消能构件的极限位移(速度)应不小于罕遇地震下消能器最大位移(速度)的1.2倍,同时还应满足此极限速度下的承载力要求。然而,即使地震区划明确,由于地壳运动的复杂性和地震作用的随机性,结构遭受的地震强度仍有可能比设防地震更大。在这种情况下,即使黏滞阻尼器的极限行程和承载力符合规范要求,由于实际地震动强度过大,其仍可能超过极限状态而破坏失效。在2011年日本3·11大地震中,一些安装在一栋消能钢结构建筑中的油阻尼器被破坏,也表明消能装置在极端地震下是可能损坏甚至完全失效的[13-14]。在实际工程中,阻尼器作为一种耗能元件,其抵抗地震的能力弱于整体结构,从而能够起到有效保护整体结构的作用。从这个角度来看,随着地震动强度的增加,在斜拉桥主要构件发生严重破坏以前考虑阻尼器发生破坏的情形也是必然的。因此,在对耗能设计的斜拉桥进行抗震分析时,有必要考虑到阻尼器失效的情况,否则将会错误地估计阻尼器给结构带来的减震效果。

目前针对阻尼器失效的情况,已有的研究大多集中在阻尼器本身的失效机理或阻尼器失效对消能减震建筑结构的影响上。如Miyamoto等[15-16]提出了黏滞阻尼器的三种极限状态,即承载力极限状态、行程极限状态及承载力-行程复合极限状态,并基于OpenSees平台建立了考虑极限状态的阻尼器模型;宋昊[17]研究了黏滞阻尼器失效对高层钢结构建筑地震响应及易损性的影响;韩建平等[18]通过对OpenSees中的Maxwell模型进行二次开发得到了考虑承载力极限状态和行程极限状态的黏滞阻尼器模型,并将其应用于钢框架结构,通过时程分析研究了阻尼器极限状态对阻尼器减震性能的影响;骈超等[19]利用Ruaumoko-2D软件建立了考虑极限状态的黏滞阻尼器模型,研究了阻尼器承载力极限、位移极限对单自由度体系地震响应的影响。然而阻尼器失效对耗能减震体系斜拉桥抗震性能影响的研究较为少见。

本文首先基于某三塔斜拉桥,采用OpenSees平台建立了有限元模型,然后在上述研究的基础上,建立了考虑极限状态的黏滞阻尼器简化模型;随后研究斜拉桥地震响应随阻尼器参数变化的规律,确定了阻尼器的各项参数;最后将考虑极限状态的阻尼器模型应用于斜拉桥中,通过时程分析研究阻尼器在大震中遭到破坏及其破坏后给斜拉桥结构响应带来的变化,分析阻尼器失效对耗能减震体系斜拉桥抗震性能的影响。

1 模型的建立

1.1 斜拉桥有限元模型

本文以某预应力混凝土三塔斜拉桥为研究对象,该桥承载双向四车道,全长768 m,跨径布置为84 m+300 m+300 m+84 m。中塔和边塔均采用双柱双索面形式,其中中塔高125.28 m,两边塔高75.78 m。桥面整体宽度为32.8 m,由预应力混凝土箱梁和桥面板组成。斜拉索由高强钢丝组成,全桥共有200根。原桥最初设计为中塔固结、边塔半漂浮体系,为研究阻尼器对斜拉桥的减震效果,首先将中塔与主梁由原来的刚性连接变为滑动铰支座连接,得到纵向漂浮体系的斜拉桥,然后在中塔和主梁之间安装阻尼器,即可得到耗能减震体系的斜拉桥。阻尼器布置如图1所示。斜拉桥设计时总是通过调整拉索索力使结构中的恒载内力分布更合理,使拉索应力和主梁弯矩尽可能均匀[20]。对于本文中的斜拉桥而言,采用同样的拉索索力,原中塔塔梁固结体系和修改后漂浮体系的主梁在恒载下的曲率延性系数对比如图2所示。漂浮体系主梁的最大曲率延性仅比固结体系高0.013,二者相差并不大。因此,在对斜拉桥结构体系进行修改时并未对拉索系统进行调整。

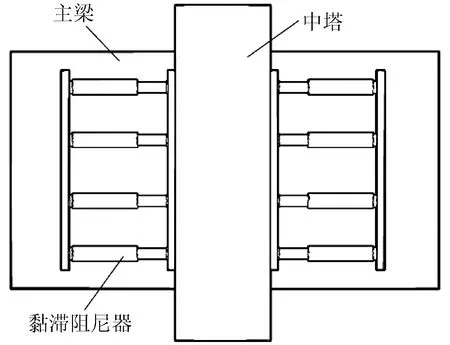
图1 阻尼器布置示意图Fig.1 Damper arrangement

图2 恒载下主梁的曲率延性系数Fig.2 Curvature ductility coefficient of main girder under constant load

基于OpenSees平台建立了全桥的三维有限元模型,如图3所示,考虑了材料和几何非线性。全桥主要由主梁、桥塔、桥面板、横梁和斜拉索组成,斜拉索由高强度钢丝组成,其余为钢筋混凝土构件。因此,使用由纤维截面定义的非线性梁柱单元来模拟主梁、桥塔、桥面板和横梁。纤维截面的混凝土和钢筋采用Kent-Scott-Park混凝土材料(Concrete 01)和双线型钢材料(Steel 01)模拟。斜拉索具有高强度、断裂时没有明显的屈服阶段和主要承受轴向拉力等特点,因此采用具有弹塑性本构模型的桁架单元模拟。

图3 斜拉桥三维有限元模型Fig.3 Three-dimensional finite element model of the cable-stayed bridge

1.2 考虑极限状态的黏滞阻尼器模型

流体黏滞阻尼器主要由缸体、活塞杆及耗能介质等组成。在地震作用下,活塞在缸体内往复运动,耗能的阻尼介质与活塞通过剧烈摩擦产生阻尼力,将地震动能转换成热能耗散掉,达到结构减震的目的。阻尼力与运动速度之间的关系为:

F=sgn(v)Cd|v|α

(1)

式中:Cd为阻尼系数;α为阻尼指数;v为活塞与缸体之间的相对速度;sgn(·)为符号函数。当前,在应用黏滞阻尼器对斜拉桥进行震动控制的研究中,常采用如图4所示的Maxwell模型来模拟阻尼器的黏弹性行为[11,21-23]。这对于大多数情况下的斜拉桥阻尼器参数设计及应用分析来说是足够的,但却没有考虑到大震下阻尼器达到承载力或行程极限的情况,无法分析这类情况下阻尼器失效对斜拉桥结构响应造成的影响。

图4 Maxwell模型Fig.4 Maxwell model

Miyamoto等[15-16]提出了黏滞阻尼器在大震下的三种极限状态:(1)承载力极限状态:阻尼力超过了阻尼器活塞杆的承受能力,活塞杆失效导致阻尼器失效;(2)行程极限状态:活塞运动达到阻尼器的最大行程,活塞接触油缸端部,此时黏滞阻尼力变为0,阻尼器相当于一个钢支撑;(3)承载力-行程复合极限状态:先达到行程极限状态,若此时阻尼器两端相对位移仍继续加大,活塞杆将因活塞与油缸端部接触导致受力过大屈服或屈曲失效,进而导致阻尼器失效。鉴于此,本研究将阻尼器简化为4个单元的组合来考虑阻尼器的极限状态,如图5所示。其中,支撑单元将阻尼力传递给结构,使用由钢材料定义的非线性梁柱单元模拟,且在分析过程中的每个时间步测量其受到的力。一旦测得的力超过极限承载力,阻尼器失效,随后在剩余的时间步长中将阻尼器模型从全桥的有限元模型中移除。根据规范[12]中的相关要求,极限承载力取为1.2倍阻尼器最大速度时的阻尼力。Hook和Gap单元代表油缸,这两个单元均使用由间隙材料定义的桁架单元进行建模。Hook单元的初始间隙和屈服应力均为负值,而Gap单元的初始间隙和屈服应力均为正值,如图6所示。两个单元的初始间隙值均取为阻尼器的行程极限值。当阻尼器的行程在极限内时,这两个单元不受力。达到行程极限值以后,这两个单元将为阻尼器提供额外的刚度。至于黏滞单元,使用具有黏滞材料的桁架单元来定义,在分析中提供阻尼器的阻尼力。

图5 具有极限状态的黏滞阻尼器简化模型Fig.5 Simplified model of viscous damper with limit states

图6 间隙材料的应变-应力模型Fig.6 Strain-stress model of gap material

2 考虑阻尼器极限状态的斜拉桥抗震分析

2.1 阻尼器参数确定

对于耗能减震设计的桥梁结构,阻尼指数的取值常为0.2～1.0[5,23]。为确定本研究中阻尼器的参数,首先应用Maxwell模型模拟阻尼器进行参数分析。设置每个阻尼器的阻尼系数Cd=500～4 000 kN/(m/s)α,间隔500 kN/(m/s)α,阻尼指数α=0.2～1.0,间隔0.1,共计72种工况。选择1999年台湾集集地震TCU052台站得到的地震动记录对具有不同阻尼器工况的斜拉桥模型进行非线性时程分析。地震动沿桥梁纵向和竖向联合输入,因原桥所在地区抗震设防烈度为7度(0.1g),按7度罕遇地震水准将峰值加速度分别调幅为0.2g和0.13g。对不同阻尼器参数下斜拉桥塔底最大弯矩、剪力和塔顶最大位移的变化规律进行分析,作为评价阻尼器减震效果的依据。

图7、图8分别为中塔和边塔各结构响应随阻尼器参数的变化情况,其中Cd=0为无阻尼器,即纵向漂浮体系的结构响应。从图7中可以看出,除了α=0.2、Cd=4 000 kN/(m/s)α这一点外,中塔底部的弯矩和塔顶的最大位移均随着阻尼系数Cd的增大和阻尼指数α的减小而逐渐减小。但中塔底部剪力的变化则不同,其随阻尼系数Cd的增大而增大,且阻尼指数α越小剪力增加的幅度就越大。至于边塔,从图8中可以看出阻尼器参数对塔底弯矩、剪力和塔顶最大位移的影响是一致的,它们均随着Cd值的增大和α值的减小而减小。无阻尼器时,桥塔与主梁之间的滑动铰支座并不能直接将主梁纵向惯性力传递给桥塔。但在中塔与主梁之间安装了阻尼器以后,产生了阻尼力,导致主梁在地震作用中向中塔传递了较大的纵向力,因此中塔底部的剪力增加,而边塔底部的弯矩和剪力减小,协调了中塔和边塔之间的响应。而中塔底部的弯矩并未增加,这与阻尼器起到的减震效果有关。以α=0.3为例,此时各Cd值下中塔沿塔身的弯矩包络如图9所示。随Cd值的增大,传递给中塔的纵向力增大,因此阻尼器安装高度以下塔身弯矩的增长速率随之增大,中塔底的剪力增大。但由于阻尼器发挥了良好的减震作用,中塔的整体反应随Cd值的增大而降低,即使剪力上升导致阻尼器安装高度以下塔身的弯矩增长速率加大,塔底的弯矩依然随Cd值的增大而减小。

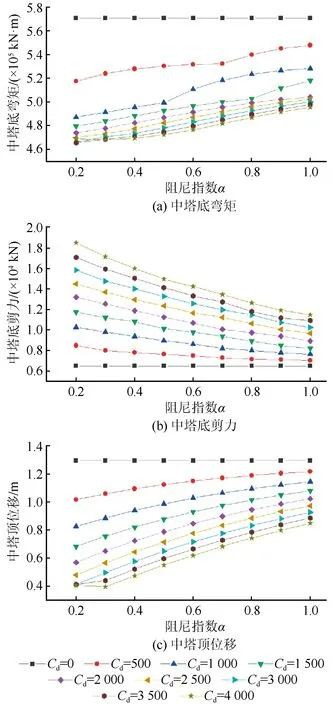
图7 中塔地震响应Fig.7 Seismic responses of the middle tower

图8 边塔地震响应Fig.8 Seismic responses of the side tower

图9 中塔沿塔身的弯矩包络(α=0.3)Fig.9 Bending moment envelope along the middle tower (α=0.3)

图10为各参数下黏滞阻尼器的阻尼力及位移。选取阻尼器应在取得良好减震效果的同时使得阻尼器的阻尼力和行程尽量小[8,11,21]。因此,为有效降低桥梁的纵向位移,控制全桥的地震响应,同时考虑生产工艺水平及造价的经济合理,选用阻尼器的Cd值为3 500,α值为0.3。此参数下阻尼器的最大位移为0.448 m,最大阻尼力为2 370 kN,按照相关规范[12,24]中的规定,选择规格为极限行程±550 mm、最大阻尼力2 500 kN的阻尼器,此时对应的阻尼器最大速度为0.326 m/s。

图10 黏滞阻尼器的阻尼力及位移Fig.10 Damping force and displacement of viscous damper

2.2 阻尼器失效对斜拉桥地震响应的影响

为分析阻尼器失效对耗能减震体系斜拉桥地震响应的影响,首先设置了3种阻尼器工况:工况1为无阻尼器的纵向漂浮体系,工况2安装Maxwell模型模拟的阻尼器,工况3安装具有极限状态的阻尼器模型。随后,将原输入地震动纵向和竖向的峰值加速度调幅到0.4g和0.26g,对不同阻尼器工况下的斜拉桥进行非线性时程分析。

(1) 阻尼器性能分析

工况2、3中阻尼器的滞回曲线如图11(a)、(b)所示。从图中可知,工况2中阻尼器的最大位移接近1.5 m,超过了阻尼器的极限行程。由于阻尼器安装在中塔和主梁之间,这也说明中塔处的主梁位移接近1.5 m。而常见的黏滞阻尼器是较难满足这样大位移需求的,因此在实际工程中应用阻尼器进行斜拉桥震动控制时,可考虑联合使用双曲面球型减隔震支座[25]等具有较强位移能力的新型减隔震支座来共同发挥耗能减震的作用,减小大震下主梁的位移响应。工况3中的阻尼器并未达到行程极限,但由于阻尼力超过了极限承载力而失效。为进一步对比承载力极限和行程极限对斜拉桥地震响应的影响,增加同样安装具有极限状态阻尼器模型的工况4,与工况3相比,将阻尼器的极限承载力提高以便阻尼器的行程可以达到极限值。工况4中的阻尼器滞回曲线如图11(c)所示,在提高了极限承载力后,阻尼器首先达到了行程极限,然后代表油缸的Hook和Gap单元为阻尼器提供了额外的刚度,导致阻尼器受力急剧上升,超过了极限承载力,随后阻尼器失效。工况3、4中阻尼器的滞回环面积明显小于工况2,表明大震下具有极限状态的阻尼器模型耗能能力低于Maxwell阻尼器模型。

图11 阻尼器的力-位移曲线Fig.11 Force-displacement curves of the damper

(2) 结构地震响应分析

对上述4种阻尼器工况下的斜拉桥地震响应进行对比。图12、图13即为不同工况下中塔和边塔的地震响应时程。其中,t=33.555 s时工况3阻尼器失效,t=35.955 s时工况4阻尼器失效。对于塔底内力而言,在阻尼器失效前,由于阻尼力的存在,中塔底部的弯矩和剪力较无阻尼结构略有增大,而边塔底部的弯矩和剪力略有降低。随着地震作用的逐渐增强,有阻尼器的斜拉桥中塔底部剪力急剧上升,在t=33.555 s附近出现了峰值。这时阻尼器达到或将要达到最大阻尼力,如图11所示,其中工况3中的阻尼器达到了承载力极限而后失效,而工况2、4中的阻尼器继续工作。在地震动的持续作用下,阻尼器的行程逐渐增大,最终在t=35.955 s时工况4中的阻尼器达到了行程极限值。此时由于阻尼器活塞触底,行程受限,工况4中的阻尼器受力急剧上升,反映在阻尼器滞回曲线上即为图11(c)中力的突然上升,反映在中塔底部剪力上即为图12(b)中代表工况4的曲线出现了一个极值。之后,工况4中的阻尼器也失效退出工作,只有工况2中的阻尼器一直在发挥耗能减震的作用。因此,工况2的中塔底部剪力在35～55 s之间变化得最为剧烈,弯矩也随剪力变化起伏较大。而在50 s附近工况3、4的中塔底弯矩和边塔底弯矩及剪力均出现了超过工况1、2的峰值,表明达到极限状态后阻尼器失效可能会给结构的减震效果带来不良影响。随后,地震作用逐渐减弱,工况2的阻尼器展现出良好的减震性能,从55 s后直到地震作用完全结束,工况2的中塔底内力和边塔底内力变化幅度均低于其余3种工况。而对于塔顶位移而言,工况1的位移最大,起伏程度也最大,工况3次之,随后是工况4,而工况2最小。这与阻尼器失效的顺序相同,工况1无阻尼器,工况3的阻尼器最先失效,其次是工况4,而工况2中的阻尼器一直在工作,发挥出了远超其实际能力的减震作用。在60 s后,工况2的中塔和边塔塔顶位移逐渐平稳,边塔塔顶位移趋于0,而其余3种工况的中塔和边塔顶部位移仍起伏较大,尤以工况1的偏离程度最大,这表明在地震作用后工况1、3、4的斜拉桥出现了永久变形或位移,桥塔产生了损伤。参考胡章亮等[26]对桥墩损伤指标的研究,以塔顶漂移比表征桥塔的损伤程度,计算工况1～4的中塔塔顶漂移比分别为3.37%、1.05%、2.74%、2.16%,边塔塔顶漂移比分别为7.23%、2.33%、6.20%、5.42%,可见工况1、3、4的桥塔损伤都比较严重,且损伤程度与阻尼器发挥的能力相关,阻尼器越晚失效,耗能越多,桥塔的损伤程度就越轻。

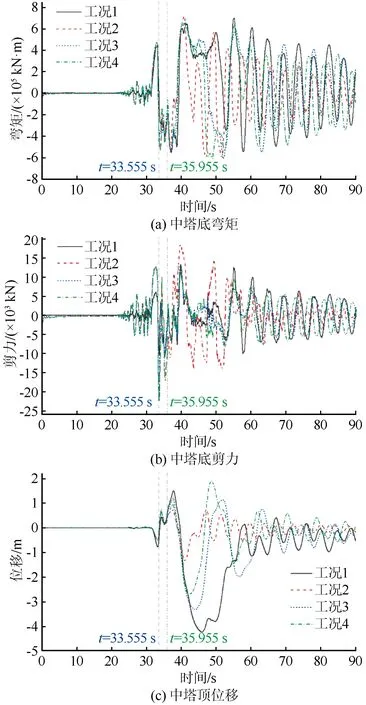
图12 不同工况下中塔地震响应时程Fig.12 Time history of seismic responses of the middle tower under various conditions

图13 不同工况下边塔地震响应时程Fig.13 Time history of seismic responses of the side tower under various conditions

图14展现了不同工况下中塔、边塔沿塔身的弯矩包络和主梁的竖向位移包络。其中,工况2由于阻尼器一直在发挥作用,使得阻尼器安装高度以下的弯矩增长速率较大,导致即使中塔整体反应较小,塔底的弯矩仍超过了其余3种工况。总的来看,工况2的桥塔弯矩包络与其余3种工况差别较大,且中塔、边塔上部的弯矩包络比其余3种工况小,说明工况2的拉索索力相对较小,而其余3种工况之间的桥塔弯矩包络较为接近。从主梁的竖向位移包络可以看出,工况3、4与工况1相比竖向位移减小的有限,而工况2的竖向位移降低幅度大,阻尼器显著地减轻了主梁的竖向震动。

图14 不同工况下中塔、边塔弯矩及主梁竖向 位移包络Fig.14 Bending moment envelope of the middle tower and side tower and vertical displacement envelope of the girder under various conditions

进一步对比不同阻尼器工况下全桥的结构响应。表1总结了各工况下斜拉桥的多个地震响应的峰值。对于塔底内力响应而言,工况2的中塔底内力峰值最大。失效的阻尼器协调中塔和边塔之间地震响应的能力减弱,因此工况3、4的中塔底弯矩低于工况2,边塔底内力则更高。工况2～4的中塔底剪力峰值基本一致,均出现在t=33.555 s附近,明显高于无阻尼器的工况1。工况2 ～4的边塔底剪力也高于工况1。对于位移响应来说,与工况1相比,工况3、4位移降低的有限,而工况2的位移显著降低。总的来看,工况2～4斜拉桥的地震响应与工况1相比有所减轻,但减轻的幅度不尽相同,工况3、4的地震响应与工况2差别很大。因此,为准确可靠地评估耗能减震体系斜拉桥的抗震能力,必须考虑到阻尼器达到极限状态后失效的情况。

表1 不同工况下结构响应峰值

3 结语

本文以某三塔斜拉桥为研究对象,分析了黏滞阻尼器的阻尼系数和阻尼指数对斜拉桥减震效果的影响,并对考虑和不考虑阻尼器失效两种耗能减震体系斜拉桥的地震响应进行了对比。根据分析结果,主要得出以下结论:

(1) 在漂浮体系三塔斜拉桥的中塔与主梁之间合理地安装黏滞阻尼器可以协调地震作用下中塔和边塔之间的响应,改善边塔塔底的受力状况,增强全桥的抗震能力。

(2) 在大震下,尤其是地震强度超出设计水平的地震下,考虑极限状态的黏滞阻尼器与Maxwell模型模拟的阻尼器相比,滞回耗能能力会有所下降,其减震效果明显降低。

(3) 对于采用耗能减震设计的斜拉桥,安装黏滞阻尼器且考虑其极限状态与安装黏滞阻尼器但不考虑其极限状态二者在大震下的地震响应差别很大,不考虑阻尼器极限状态将高估斜拉桥的抗震能力。因此,在对斜拉桥进行阻尼器设计时,应为阻尼器的承载力和行程预留充足的余量,或联合应用减隔震支座等多种减震措施降低对阻尼器能力的需求。此外,在评估此类斜拉桥的抗震能力时,可采用考虑极限状态的阻尼器模型或其他考虑阻尼器失效的方法来获得更加可靠的结果。