基于位移的模块式加筋土挡墙抗震设计方法研究

李思汉, 蔡晓光, 景立平, 蔡博渊, 刘巍巍, 马汭锦

(1. 防灾科技学院 地质工程学院, 河北 三河 065201;2. 河北省地震灾害防御与风险评价重点实验室, 河北 三河 065201;3. 廊坊市加筋土结构研发与应用重点实验室, 河北 三河 065201; 4. 中国地震灾害防御中心, 北京 100029;5. 中国地震局工程力学研究所 地震工程与工程振动重点实验室, 黑龙江 哈尔滨 150080;6. 北京市建设工程质量第二检测所有限公司, 北京 100045)

0 引言

加筋土挡墙因其经济环保、抗震性能优越等优势被广泛应用于公路、铁路等基础设施建设领域。作为一类柔性支挡结构,加筋土挡墙依靠自身变形来发挥筋材与回填土的摩擦机制、剪胀机制,维持结构的稳定[1]。然而变形过大则会严重影响结构的正常使用:Koerner等[2]分析了320座加筋土挡墙的失效原因,其中99座因变形过大而导致破坏,破坏率占比31%;Ling等[3]分析集集地震中一座加筋土挡墙破坏原因,认为筋材间距过大导致约束力不足,引起面板变形破坏;部分国家规范[4-5]对挡墙的水平位移限值进行了规定,但并未介绍采用哪种计算方法确定位移;王兰民等[6-7]认为,现有设计理论并未将变形问题纳入设计体系,现阶段缺乏公认评价体系导致基于位移的抗震设计方法无法实施。

为探究更贴近实际情况的位移设计方法,众多学者针对地震作用下的位移指数(即结构最大水平位移与整体高度之比)和位移计算方法进行了大量研究工作。

部分学者采用震后调查、振动台试验、数值模拟等手段对支挡结构的位移指数进行了研究:张建经等[8]以重力式挡墙震后位移为基础数据,提出了1%(小震)、3.5%(中震)、6%(大震)的三级抗震位移指数;朱宏伟等[9]考虑加筋土挡墙变形适应能力,提出了4%的位移控制指数;蒋建清等[10]将格宾加筋土挡墙的位移指数定为1.5%(小震不坏)、5%(中震可修)和7%(大震不倒);李思汉等[11]将模块式加筋土挡墙的位移指数定义为1.5%(基本完好)、1.85%(轻微破坏)、3.8%(中等破坏)、大于3.8%(毁坏);Huang等[12]建议无黏性土加筋土挡墙的允许位移和灾难性破坏位移指数分别定义为2%和5%。Yazdandoust[13]分别用0.2%～0.8%和4.5%～4.9%代表加筋土挡墙准弹性到塑性的过渡状态和从塑性到破坏的过渡状态。Kuwano等[14]将3%作为恢复能力极限状态和正常使用极限状态的临界值。

部分学者采用归纳统计、对比分析等方式对位移计算方法进行了分析:Cai 和 Bathurst[15]回顾了挡土墙不同计算方法,并用三次实测地震参数进行了计算对比,认为不同方法所得结果均在合理的区域;李婷等[16]将水平位移分解成加筋区内延展筋材伸长变形和加筋区及面板整体在土压力作用下的水平位移两部分,采用胡克定律和虚功原理进行了求解;卢谅等[17]以Mindlin位移理论和拟动力法为基础,提出了加筋土挡墙水平位移分区计算公式;王丽艳等[18]采用瑞利-里兹法和拟静力法建立了地震作用下的位移计算公式。

综上可知,现有位移控制指标和计算方法并未考虑不同面板型式影响:面板型式不同,变形能力不同,构造亦不同,不可一概而论,还需根据面板特点,提出针对具体类别的位移设计方法。本文归纳现有部分计算方法、求解不同破坏模式下的屈服加速度系数(即地震时导致挡墙产生滑动时的加速度值与重力加速度的比值)、结合模块式加筋土挡墙振动台试验结果对比分析,推荐适合计算模块式加筋土挡墙位移的方法,最终提出基于位移的模块式加筋土挡墙抗震设计流程。研究结果可为支挡结构性态设计理论的发展提供数据支撑和研究思路。

1 振动台试验

1.1 试验概述

模块式加筋土挡墙振动台试验在防灾科技学院的中国地震局建筑物破坏机理与防御重点实验室进行,具体介绍可见文献[11,19-21]。根据振动台承载能力和模型箱尺寸,相似比设定为2,试验模型尺寸为2.0 m(长)×1.5 m(宽)×1.8 m(高),如图1所示。试验过程中施加白噪声、卧龙波(WL)和El-Centro波(El),输入波形及加载工况(表1)参见文献[11,19-21]。根据试验设计,对模型所用回填土、筋材、面板及传感器布设逐一进行介绍。

图1 试验模型简图(单位:mm)Fig.1 Diagram of test model (Unit:mm)

(1) 回填土

回填土采用级配不良的中砂,其颗粒级配曲线如图2所示。回填土密度为1.82 g/cm3。在相对密实度为70%的设定下,回填土采取分层填筑夯实。

图2 颗粒级配曲线Fig.2 Particle-size distribution curve

(2) 筋材

筋材采用高密度聚乙烯单向土工格栅,参考ASTM D6637[22]进行拉伸试验,可得土工格栅的抗拉强度分别为T2%=17.4 kN/m、T5%=32.7 kN/m及Tult=50 kN/m。

(3) 面板

面板采用预制砌块错缝搭接而成,采用的模块尺寸分别为0.25 m(长)×0.15 m(宽)×0.15 m(高)和0.125 m(长)×0.15 m(宽)×0.15 m(高)。土工格栅与模块通过塑料卡扣进行连接,见图3所示。

(4) 传感器布设

为测试模型的面板位移模式,在模型中布设了12支位移计。位移计布设在每层面板中心位置,记录地震作用下面板峰值位移(P)和永久位移(R)。同时,在模型箱上布设2个加速度传感器用于记录输入加速度时程。

1.2 位移模式

取D1～D12采集到的位移时程,可获得模型的峰值位移和永久位移分布规律,如图4所示。

由图4可知,峰值位移和永久位移分布趋势相似,均为顶部位移最大,整体趋势呈非线性增加:①当峰值加速度不超过0.4g时,永久位移值略小于峰值位移值,挡墙几乎没有恢复;②当峰值加速度超过0.4g时永久位移值小于峰值位移值,大部分峰值位移在震后得到了恢复。除此之外,模型底部也发生了永久位移,可知挡墙的位移模式为平移与绕墙趾转动耦合,如图5所示。

图5 墙体位移模式Fig.5 Displacement mode of retaining wall

将挡墙的平行位移、转动位移和顶部永久位移分别用DT、DR和D表示,由此可通过DT/D和DR/D表示平移百分比和转动百分比,如图6所示。数据显示:墙体位移模式随着峰值加速度增大,平移模式占比逐渐减少,转动模式占比逐渐增大;当输入地震动超过0.4g时,转动模式占据主导地位。

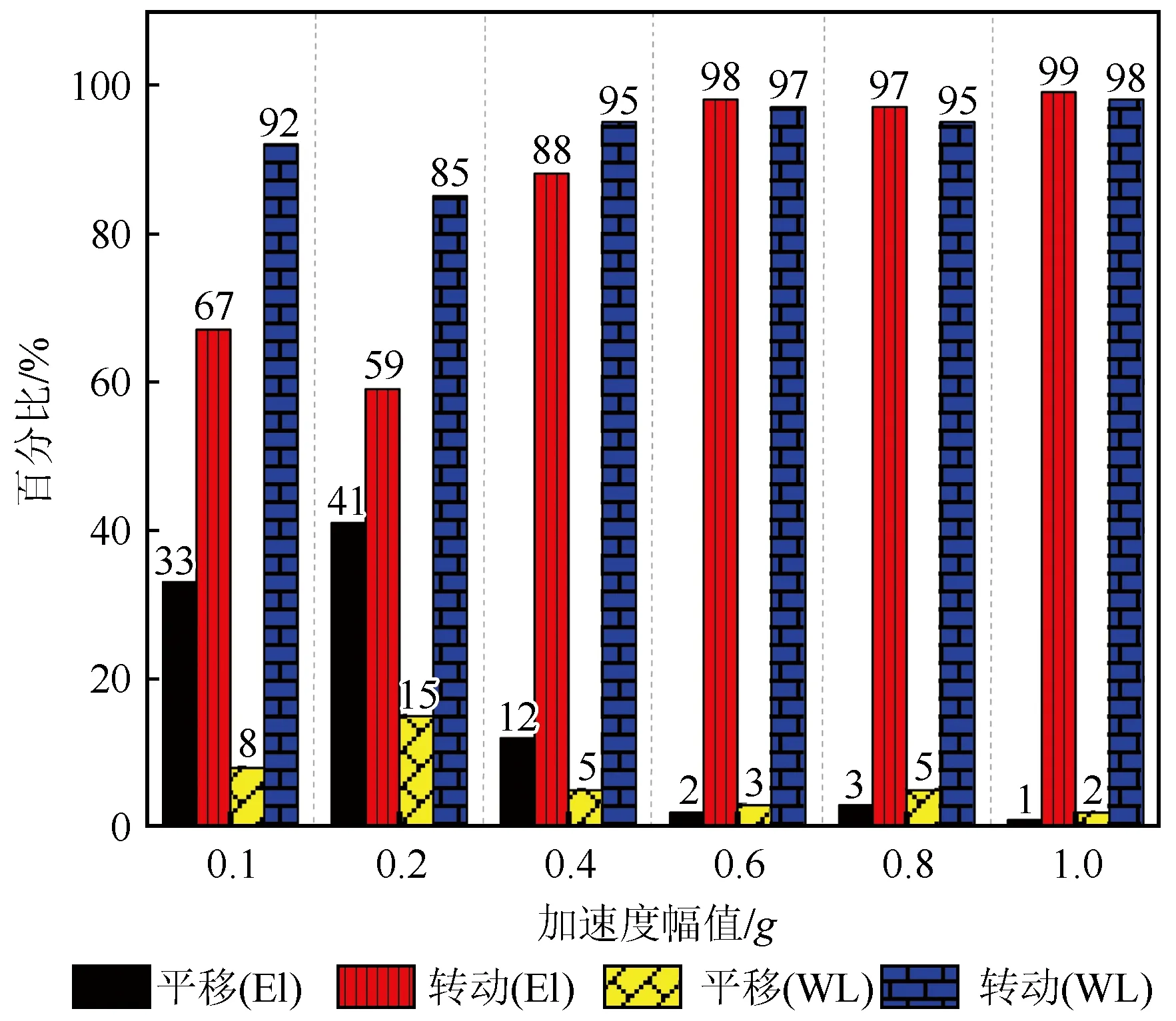
图6 平移占比与转动占比Fig.6 Translation percentage and rotation percentage

2 位移计算

2.1 位移计算公式

表2所列为地震作用下挡墙水平位移的部分计算公式[15]。各公式均将滑动体视为刚塑性滑块,且位移模式为基底滑移模式。各参数代表的物理含义分别为:d为挡墙实际水平位移;vm为水平峰值速度(即地面某点的地震动速度时间过程的水平绝对最大值);km为水平峰值加速度系数(即地震时某一点地面水平加速度最大值与重力加速度的比值);kc为水平屈服加速度系数(即地震时导致挡墙发生水平滑动时的加速度值与重力加速度的比值);g为重力加速度。

表2 水平位移计算方法

2.2 屈服加速度确定

由水平位移计算方法可知,计算过程中需确定km、vm、kc三个关键参数。其中,km、vm可通过监测到的地震动时程和场地条件确定,而kc可通过安全系数法、能量守恒法及简化算法进行确定。安全系数法[23]指在不同破坏模式(例如基底滑移、模块错动、整体倾覆等)下,求解安全系数为1.0时对应的水平加速度系数(即为屈服加速度系数)的方法。能量守恒法[24-25]是利用内功(筋土摩擦、填土黏聚力所消耗能量)和外功(挡墙自重及地震力做功)相等求解屈服加速度系数。简化算法[10,26-27]是通过分析影响屈服加速度幅值的相关因素再进行多元回归求得屈服加速度系数的方法。

由振动台试验可知,模块式加筋土挡墙永久位移模式整体为平移与转动耦合,局部则属于模块错动。故仅列出部分安全系数法(模块错动、基底滑移、整体倾覆)、能量法及简便算法相关公式,如表3所列。

不同破坏模式下屈服加速度系数与安全系数间的关系,见图7所示。由图7(a)和(b)可知:(1)屈服加速度系数和安全系数随着峰值加速度和挡墙高度增加而逐渐减小,模型顶部最小;(2)顶部模块易发生错动、倒塌,这种现象与挡墙的稳定性无关,其原因是顶部自重及约束小造成。由图7(c)和(d)可知:(1)0.6g时,基底滑移模型的屈服加速度为0.64g,大于输入地震动,故不会出现平移现象;(2)0.6g时,整体倾覆模型的屈服加速度系数为0.24,小于输入地震动,会出现整体倾覆现象;(3)将图(c)、图(d)对比可知,整体倾覆模式的屈服加速度系数在各个地震动情况下均小于基底滑移下的屈服加速度系数,这与振动台试验中位移模式转动为主,平动为辅一致。

图7 屈服加速度与滑动安全系数关系Fig.7 Relationship between yield acceleration and sliding safety factor

吴书旭[26]、朱宏伟等[10]采用的屈服加速度系数,其前提为加筋间距为0.3 m或0.6 m,这与试验中模块式挡墙的基本情况不符,故不在文中进行计算。Muni[27]和Ausilio[25]所用的屈服加速度计算公式虽涉及加速度,但并未涉及主要研究的水平加速度,故计算值为常数:0.34和0.36。

2.3 计算结果对比

将模块式挡墙的实测值与Newmark上限法、Cai and Bathurst平均上限法、Richards and Elms上限法和Whitman and Liao平均拟合法进行对比,以确定各类计算方法的差异。

计算过程中所用参数km和vm采用Matlab处理,见表4所列。关于屈服加速度,有如下3点需要说明:(1)在模块错动模式下,仅有0.4g、0.6g地震动作用下顶部出现安全系数小于1的情况,故仅分析0.6g时实测值与计算值的不同;(2)基底滑移模式在0.1g～0.6g输入时,无平移情况,整体倾覆在0.6g时才开始移动,与实际情况不符,故不在此进行分析计算;(3)采用Muni和Ausilio方法计算出的屈服加速度进行对比分析。

表4 峰值加速度和峰值速度

图8为0.6g时模块错动模式下实测永久位移值与各类方法计算值的对比情况。由图可知:(1)各类方法计算所得位移在顶部出现激增,且位移值大小为Richards and Elms上限法>Cai and Bathurst平均上限法>Newmark上限法>Whitman and Liao平均拟合法;(2)顶部实测值远小于各类计算方法,各类方法误差较大且保守。可见,采用模块错动模式进行位移计算不符合实际情况。

图8 WL0.6g时不同计算方法对比Fig.8 Comparison between different calculation methods under WL0.6g

由于各类计算方法的应用前提为滑移模式,故在进行计算对比时,仅将实测值顶部永久位移值与各类计算方法计算值进行对比。采用Muni方法和Ausilio方法得到屈服加速度后,采用各类计算方法的对比情况见图9所示。由图可知:(1)各类计算方法所得位移值大小为Richards and Elms上限法>Cai and Bathurst平均上限法>Newmark上限法>Whitman and Liao平均拟合法,这与模块错动模式计算结果一致;(2)当峰值加速度小于0.6g时,各类计算方法计算值与实测值相差较小,均在一个合理的区间范围内,这与Cai and Bathurst[15]分析结论一致;(3)当峰值加速度在0.4g及0.4g以下时,各类计算方法所得结果均小于实测值,可采用Richards and Elms上限法进行位移预测;(4)当输入幅值为0.6g时,各类方法计算结果增幅逐渐增大,采用Cai and Bathurst平均上限法进行位移计算较为符合实际;(5)当输入幅值为0.6g～0.8g时,各类方法计算结果增幅逐渐增大,采用Newmark上限法计算位移较为符合实际;(6)当输入地震动为0.8g～1.0g时,各类计算方法差距加大,Whitman and Liao平均拟合法计算位移较为合适。

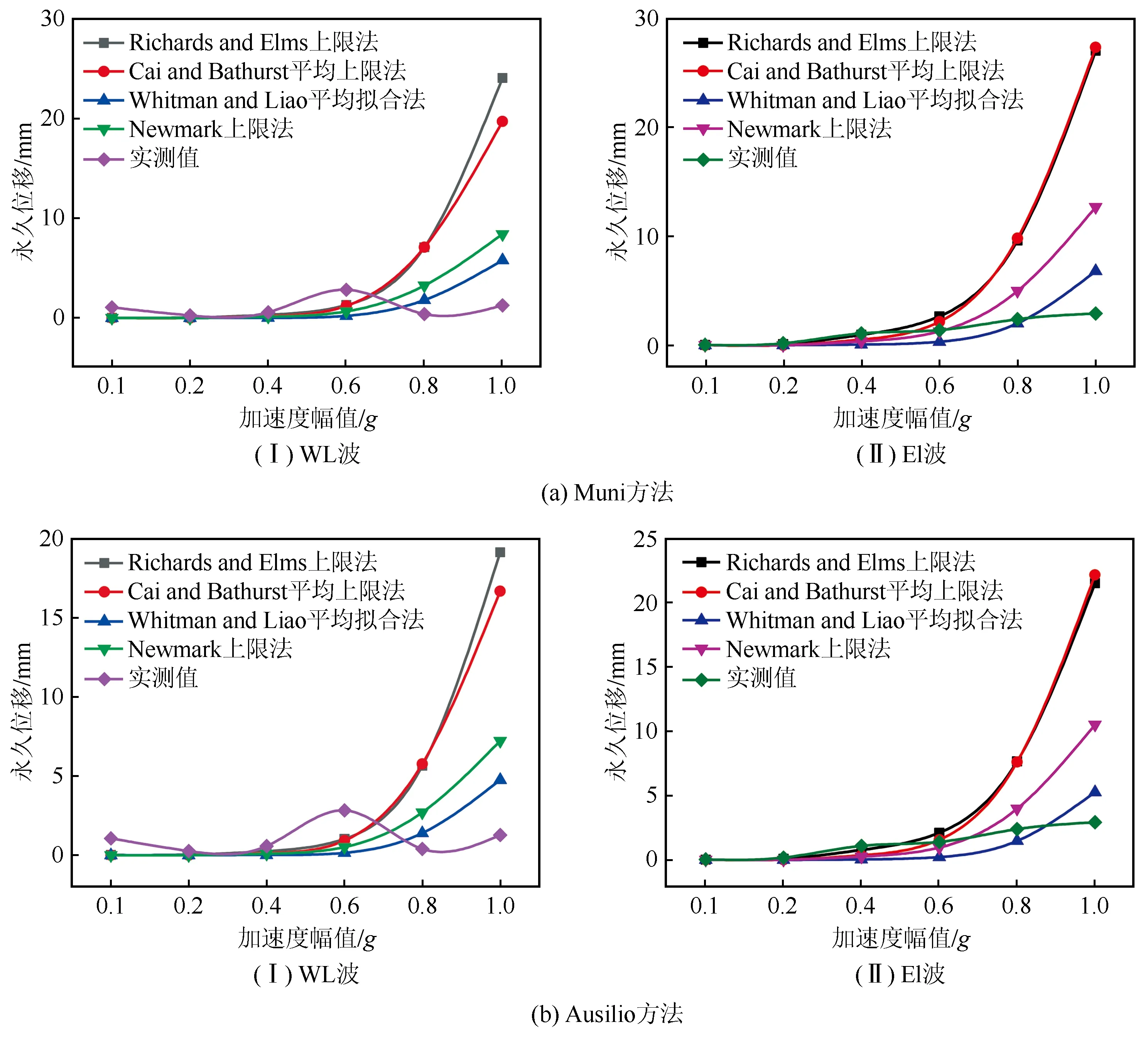
图9 不同计算方法对比Fig.9 Comparison between different calculation methods

3 基于位移的抗震设计流程

现有挡墙的设计流程主要包括两方面:静力稳定性验算和地震稳定性验算。其中,静力稳定性验算包括外部稳定性验算(抗滑移、抗倾覆、偏心距、地基承载力)和内部稳定性验算(筋材强度、筋材抗拔、筋材与面板连接强度等);地震稳定性验算亦分为内部稳定性验算和外部稳定性验算。由于加筋土挡墙的柔性特征,基于位移的抗震设计方法已被广泛关注。张建经等[31]归纳了重力式挡墙基于位移的抗震设计流程,本节借鉴其思路归纳出基于位移的模块式加筋土挡墙抗震设计流程:

(1) 根据挡墙的变形能力和破坏程度确定破坏程度位移指标。位移控制指数<1.5%时,挡墙基本完好,可正常使用;当位移控制指数在1.5%～1.85%时,挡墙轻微损坏,可正常使用和正常维修;位移控制指数在1.85%～3.8%时,挡墙发生中等损坏,需要采取交通管制、限制车辆载重和数量的措施,可用于抢险救灾,短时间内可修复;当位移控制指数>3.8%时,挡墙破坏,应停止使用,采取紧急措施修复或重建。

(2) 根据经验公式(Muni方法或Ausilio方法)确定屈服加速度,根据区域特性确定峰值加速度、峰值速度和特征周期。

(3) 0.4g地震动及0.4g以下时,采用Richards and Elms上限法对加筋土挡墙震后永久位移进行计算,并将位移值换算成位移控制指标进行评估。

(4) 若位移指标不满足要求,则调整相关参数,重复上述(1)、(2)和(3)步骤,直至满足设计要求。

研究结果将位移控制的抗震设计方法并入原有的挡墙设计流程中,按照静力稳定性验算、地震稳定性验算和位移抗震设计三方面进行挡墙设计。

4 结论

(1) 峰值位移和永久位移随峰值加速度增加而增加。挡墙位移模式为平移与绕墙趾转动耦合,且以转动为主。

(2) 模块错动、基底滑移和整体倾覆这三种破坏模式所得屈服加速度值偏大,位移计算结果与实测结果不符。采用Muni方法和Ausilio方法所得屈服加速度为常数值。

(3) 当峰值加速度在0.4g及0.4g以下时,可用Richards and Elms上限法进行预测位移量;当输入幅值为0.6g时,采用Cai and Bathurst平均上限法进行位移量预测;当输入幅值为0.8g时,采用Newmark上限法预测位移量;当输入地震动为0.8g～1.0g时,采用Whitman and Liao平均拟合法预测位移较为合适。

(4) 归纳了模块式加筋土挡墙基于位移得抗震设计流程。

文中提及的位移计算方法均是基于滑移模式计算,所得位移即为挡墙最大永久位移,与实际挡墙位移模式有所不同。位移限值中无论何处出现最大位移,均可认为发生损伤,因此可暂时采用此类方法确认变形情况。更加合理、准确地计算理论,有待进一步深入研究。