串列式双风轮风电机组气动特性建模及仿真
胡 阳, 王浩楠, 房 方, 许昱涵, 刘吉臻
(1.新能源电力系统国家重点实验室,北京 102206;2.华北电力大学 控制与计算机工程学院,北京 102206)
随着人类对能源需求的日益加剧,面对“碳达峰、碳中和”的战略目标[1],建设新型清洁能源电力系统已是大势所趋。风力发电(以下简称风电)是清洁能源的主要形式之一,风电机组具有建设周期短、机组寿命长、可靠性高和运行维护简单的特点,因此受到广泛关注[2]。风电机组中气动系统通过降低空气流速吸收空气动能,将风能转换为风轮旋转的机械能[3];由于空气动力学特性使风能捕获过程出现复杂的本质非线性[4],给风电过程的建模带来了严峻的挑战,因此对风电机组气动非线性系统的建模研究非常重要。
传统风电机组气动系统建模为叶素动量理论建模[5],该模型为白箱模型,结构比较复杂。文献[6]~文献[7]研究了风电机组的气动系统静态非线性参数辨识问题,分别运用六参数模型和八参数模型进行研究,复杂度较高。气动系统建模还有Cp-λ-β曲线建模,包括函数法和表格法,其中Cp为风能利用系数,λ为叶尖速比,β为桨距角。该模型可以描述气动系统的静态特性,但无法表征2个静态之间的超调等暂态现象。Zhao等[8]将风机非线性气动模型识别并转换为离散的基于聚类的线性分段仿射(PWA)模型,通过对多维工作域进行分类并优化重组区域来估计线性子模型,该模型与某些选定工作点的线性化相比具有一定优势。潘晨阳[9]在建立气动PWA模型表征气动系统全局特性的同时,使用神经网络对误差进行补偿,结果表明使用该模型跟踪气动机械转矩,可以改善模型精度。
新型串列式双风轮风电机组在发电机的两侧装设前、后2个风轮,相较于传统单风轮机组,风能利用率有所提高。新型串列式双风轮风电机组应用了新型高效的对转式异步发电机,结构相对简单,是一种具有广阔应用前景的新型风能转换装置。双风轮风电机组气动部分模型的搭建不同于单风轮风电机组,其前、后2个风轮之间存在无法忽略的气动耦合关系[10],这使得双风轮风电机组气动部分具有高度复杂的非线性。因此,解决双风轮风电机组气动部分的非线性问题,对实现气动部分的建模仿真具有重要意义。李新凯等[11]考虑前、后风轮各诱导因子和气动耦合系数,确定了双风轮风电机组气动系统性能与双风轮风功率的变化趋势,适用于双风轮机组气动性能设计。No等[12]利用双风轮机组的一般运动方程,采用叶片单元和动量理论,以及流动相互作用原理构造了气动系统计算模型。史运涛等[13]推导了具有多输入多输出(MIMO)复杂形式的混杂系统的分段仿射自回归(PWARX)模型的表达式并实现了模型辨识,该模型可应用于各种具有复杂非线性特性的系统,但目前鲜有相关研究提出双风轮风电机组气动部分PWARX建模表述。
笔者提出一种以双风轮风电机组为研究对象的气动MIMO系统全工况PWARX建模方案。该方案考虑输入输出数据的延迟影响,通过双风轮风电机组机理分析结合系统辨识定阶构建有限差分回归向量,针对双风轮风电机组全工况运行数据,以前、后风轮气动转矩为输出,采用高维聚类直接对有限差分空间凸划分并估计子模型边界超平面,得到若干作用域。根据模型结构辨识线性子模型参数,集成实现双风轮风电机组气动MIMO系统全工况动态表征。最后,基于所搭建的双风轮风电机组半物理仿真平台进行仿真分析,以验证该方案的有效性。
1 MIMO形式的PWARX建模结构
以PWARX模型为基本结构,假设输入量含h维,即u(k)=[u1,u2,…,uh]T∈Rh,输出量含d维,即y(k)=[y1,y2,…,yd]T∈Rd,该形式单输出的S个子模型结构[14-15]可表示为:
(1)
式中:yg(k)为模型第g个输出量,g=1,…,d;μg,i=[ag1,iT,ag2,iT,…,agna,iT,bg1,iT,bg2,iT,…,bgnb,iT,fg,i]T为模型参数向量,其中ag1,i,ag2,i,…,agna,i和bg1,i,bg2,i,…,bgnb,i分别为第i个子模型各阶输出和输入对应的系数,维数为d维和h维,fg,i为偏移量;x(k)=[yT(k-1),…,yT(k-na),uT(k-1),…,uT(k-nb)]T=[x1(k),x2(k),…,xi(k),…,xn(k)]T为有限差分回归向量,n=dna+hnb;na和nb分别为模型输出量和输入量的延迟阶次;χi为第i个子模型作用域。
基于该模型结构直接对多个输出建模,得到的MIMO系统PWARX模型可描述为:
(2)
根据已知的数据集计算模型的参数向量和作用域,建模步骤如下:
(1) 考虑MIMO数据间延迟特性,定义含多个输出的有限差分回归向量x(k),找出每个数据点与附近拥有最小欧氏距离的c-1个点建立局部数据子集Ck。在每个数据子集中形成特征向量ξk,ξk由数据子集的参数向量λk结合数据子集中各点的均值θk构成,即ξk=[λkT,θk]T。
基于文献[15]中对λk的算式分析,推导出直接计算MIMO系统数据集参数向量的方法。该数据集参数向量的维数与输出量个数有关,通过最小二乘法计算,表达式如下:
(3)
式中:yCk,i为Ck中样本第i个输出量。
(2) 计算λk的经验协方差矩阵Vk[15],用各数据集回归向量计算各类数据的离散度矩阵Lk:
(4)
将特征向量ξk看成遵循高斯分布的随机向量,其协方差可估计为Rk=[Vk,0;0,Lk],使用K-means算法[16]对特征向量聚类,构造S组有限差分数据集,记为D1,D2,…,DS。
(3) 把聚类得到的S组数据作为各子模型参数辨识时使用的数据,以特征向量的置信度ωk[17]作为数据集的权重,采用加权最小二乘法辨识可得到各子模型的参数μi。子模型作用域的边界可采用软间隔支持向量机(SVM)求取超平面方程的系数[18]。算法优化目标公式如下:
s.t.tk(φTxk+q)≥1-δk,δk≥0
(5)
式中:J为目标函数;φ为不同工作域切平面的法向量;η为范围可从0变化到1的惩罚系数;δk为松弛变量,反映了数据不满足硬间隔约束的水平;tk为可取不同数值的数据分类标志;q为偏移量;m为总数据量。
2 双风轮机组气动特性建模
将上述模型结构应用于双风轮风电机组气动特性,双风轮气动转矩的输出值与前后风轮输入输出数据具有复杂的非线性关系,可表示为:
Tr=fTr(V,ωr1,ωr2,β1,β2,Tr1,Tr2)
(6)
式中:Tr为模型气动转矩输出值;Tr1、Tr2分别为前、后风轮气动转矩,N·m;V为来流风速,m/s;ωr1、ωr2分别为前、后风轮转速,r/min;β1、β2分别为前、后风轮桨距角,(°);fTr为非线性函数。
考虑前、后风轮间的干涉特性,设置输入向量含5维,u(k)=[u1,u2,u3,u4,u5]=[V,ωr1,ωr2,β1,β2]T∈R5;输出变量含2维,y(k)=[y1,y2]=[Tr1,Tr2]T∈R2。根据上述建模方案,建立双风轮气动MIMO系统全工况PWARX模型,具体建模过程如图1所示。

图1 双风轮机组气动MIMO系统全工况PWARX建模方案
采用上述模型结构定义有限差分回归向量时,考虑各回归向量中不同变量单位不同、数值相差很大等因素的影响,为了提高模型精确度,在建模前对回归变量归一化[19]处理表示如下:
(7)
式中:xnorm(i)为归一化值;xmin(i)和xmax(i)分别为变量x(i)的最小值和最大值。
在进行高维聚类的过程中,当高维空间聚类取得的效果较好时,却可能在三维空间展示时表现为不满足预期的情况,此时可采用聚类性能评价指标量化,如果指标尚可,那么聚类效果就认为达到预期。引入戴维森堡丁指数(DBI),DBI指标RDBI考虑聚类数据簇内紧密性和簇间分散性,越小表明聚类效果越好,定义如下:
(8)
式中:N为聚类簇个数;Si、Sj分别为簇i、簇j数据各点到簇质心的平均距离,用于度量样本间的紧密程度;Mi,j为簇i与簇j质心间的距离,用于度量不同簇样本间的分散程度。
根据式(2)的结构对各子模型参数进行辨识并划分作用域后,集成子模型逼近双风轮气动全局非线性特性建立双风轮气动MIMO系统的PWARX模型。为评价模型性能引入模型性能评价指标,定义均方根误差(ORMSE)、平均绝对误差(OMAE)和平均绝对百分比误差(OMAPE)。指标越小,表明模型性能越准确。
(9)
(10)
(11)
式中:ye(i)为预测值;y(i)为实际值。
3 仿真分析
3.1 半物理仿真平台设计
为验证所提方法的有效性,选取双风轮风电机组半物理仿真平台运行数据进行仿真验证,平台搭建一套不改变双风轮运行原理及能量流动方向的软硬件设备并设计相应的控制系统,仿真双风轮机组发电过程,验证其运行性能。平台主要包括风机仿真模型、硬件可编程逻辑控制器(PLC)主控系统和上位机监控系统,各系统间使用OPC通信协议进行变量的通信交互,通信采样间隔为0.1 s,设计架构如图2所示。
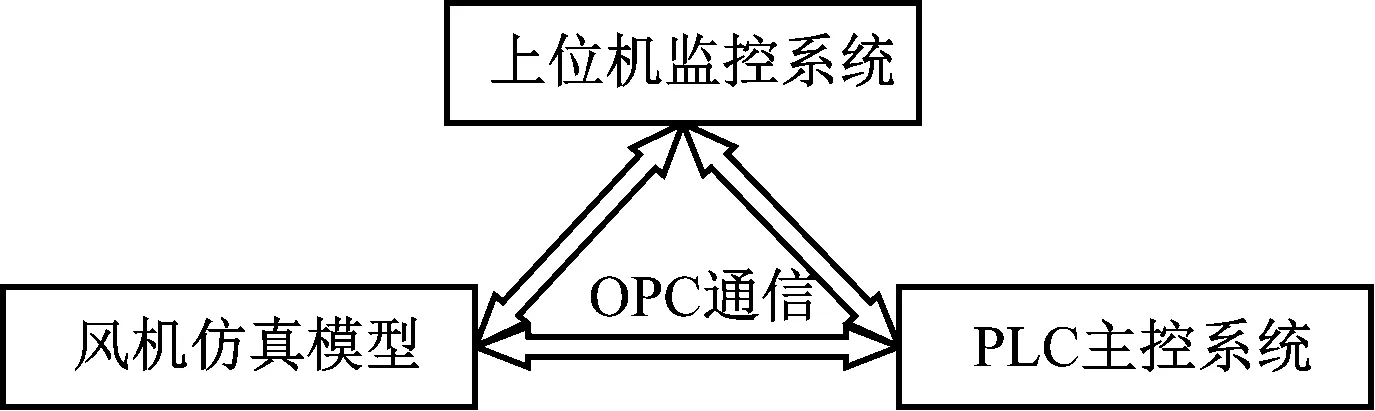
图2 半物理仿真平台架构设计图
半物理仿真平台中的风机仿真模型设计首先基于双风轮风电机组有限元分析建模仿真和寻优,得到双风轮非线性气动特性参数,见表1。

表1 双风轮风电机组气动参数
利用前后风轮气动参数、气动干涉特性和叶素动量理论建立双风轮叶素动量模型,基于该叶素动量模型设计流体力学特性仿真实验,得到若干组双风轮运行数据,根据其中一组实验数据,得到风速范围为3~15 m/s、精度为1 m/s时理想前后风轮转速和桨距角,使机组最大程度利用风能获得最大的风能利用系数(Cp,定义为Cp1+Cp2,其中Cp1、Cp2分别为前后风轮的风能利用系数),得到最佳运行工况,见表2。
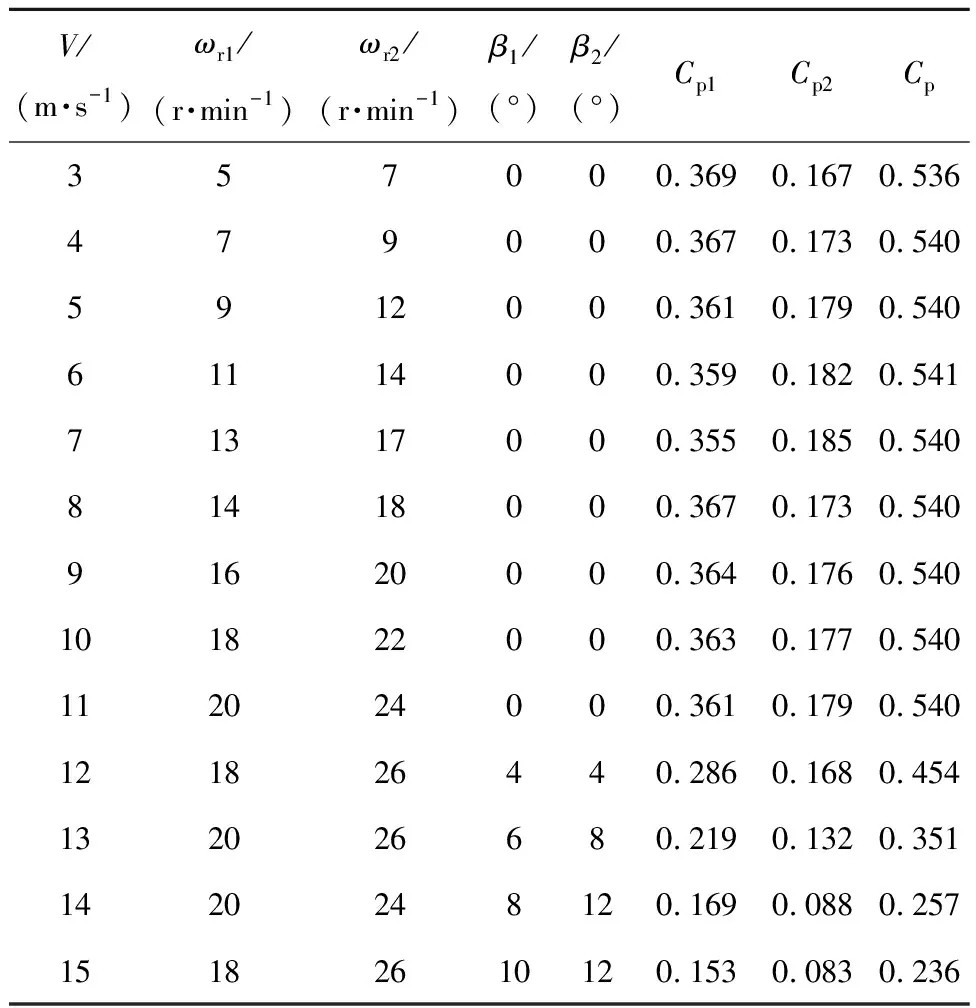
表2 最佳运行工况表
根据表2,以及其他几组不同物理量、维度及精细度的实验数据分析双风轮风电机组运行特点,制定双风轮风电机组全工况覆盖的运行区间。整体区间划分结果主要分为最大功率跟踪区、过渡区和恒功率区,如图3所示。
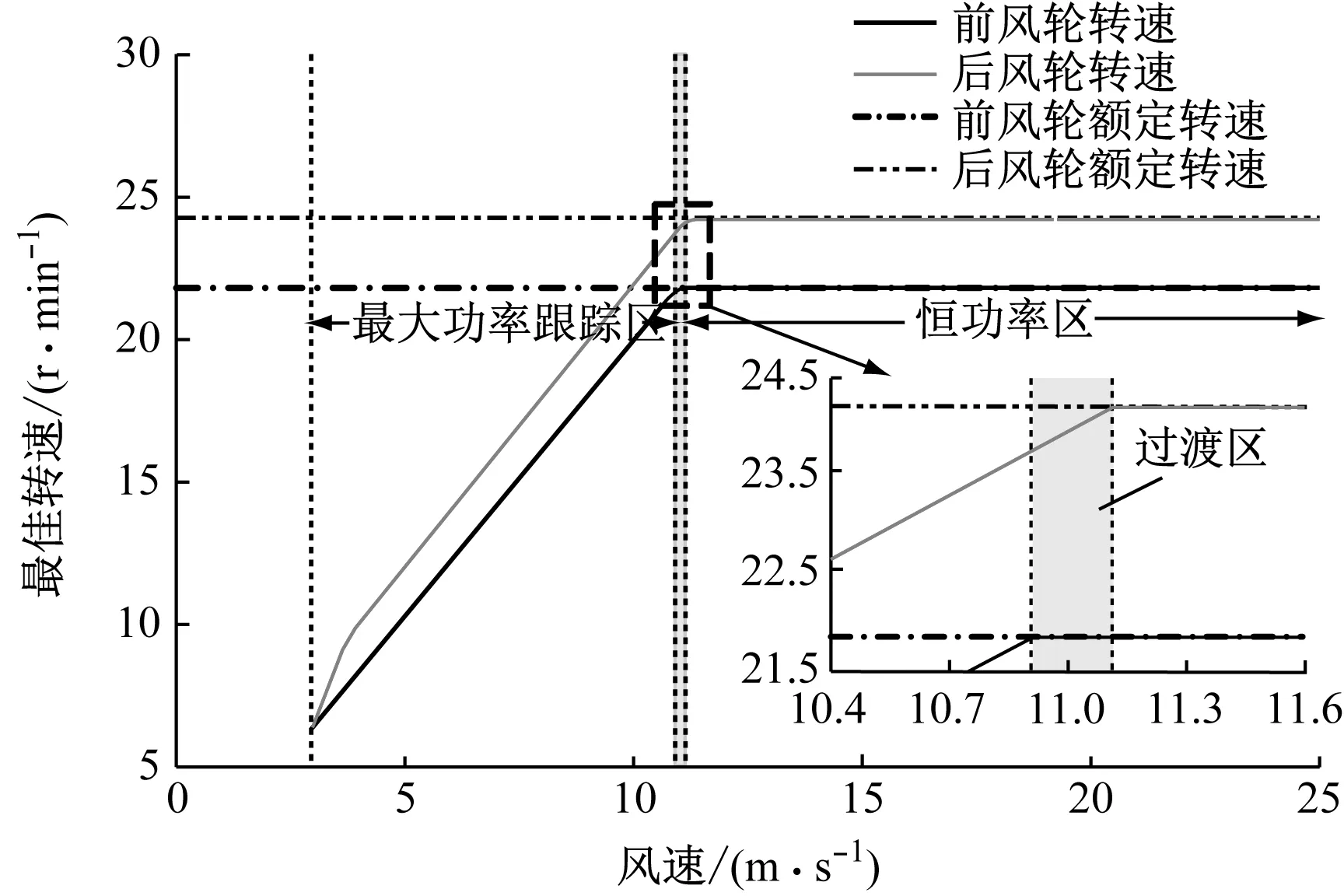
图3 双风轮机组全工况运行区间
根据双风轮风电机组全工况运行区间划分结果,在硬件PLC中设计相应的控制算法,并在上位机监控系统中实现对风机仿真模型和硬件PLC的变量交互通信,完成整个双风轮风电机组半物理仿真平台的搭建。
3.2 建模数据采集
选取在半物理仿真平台运行的3~22 m/s全工况风速场景下生成的17 127组运行数据为建模数据,包括来流风速、前后风轮转速、前后风轮桨距角和前后风轮气动转矩,如图4所示。

(a)
3.3 基于高维聚类的PWARX建模
根据双风轮机理信息结合系统辨识确定延迟阶次na=2,nb=1。对数据归一化后构造有限差分空间x(k)=[Tr1(k-1),Tr1(k-2),Tr2(k-1),Tr2(k-2),V(k-1),ωr1(k-1),ωr2(k-1),β1(k-1),β2(k-1)]T。聚类时设置局部数据子集个数c=50,根据机组运行区间特性选择工作域个数为S=3。
对特征向量聚类后,选取每类数据集有限差分回归向量第5、6、8组数据展示前风轮聚类结果,如图5(a)所示,选取第5、7、9组数据展示对应后风轮聚类结果,如图5(b)所示。

(a) 前风轮
经聚类后,由聚类量化指标计算可知RDBI为0.141 5,因此认为此次聚类结果达到预期目标。各子模型按照式(12)的模型结构,基于各工作域数据子集对模型参数进行辨识,辨识结果见表3。针对相临数据集采用软间隔SVM得到边界超平面方程ωTx+b=0,系数ωT和b的结果见表4。χ1和χ2分别为第1、2个子模型和第2、3个子模型的超平面系数;根据上述子模型参数和边界超平面对应得到包含3个工作域的双风轮风电机组气动MIMO系统全工况PWARX模型。
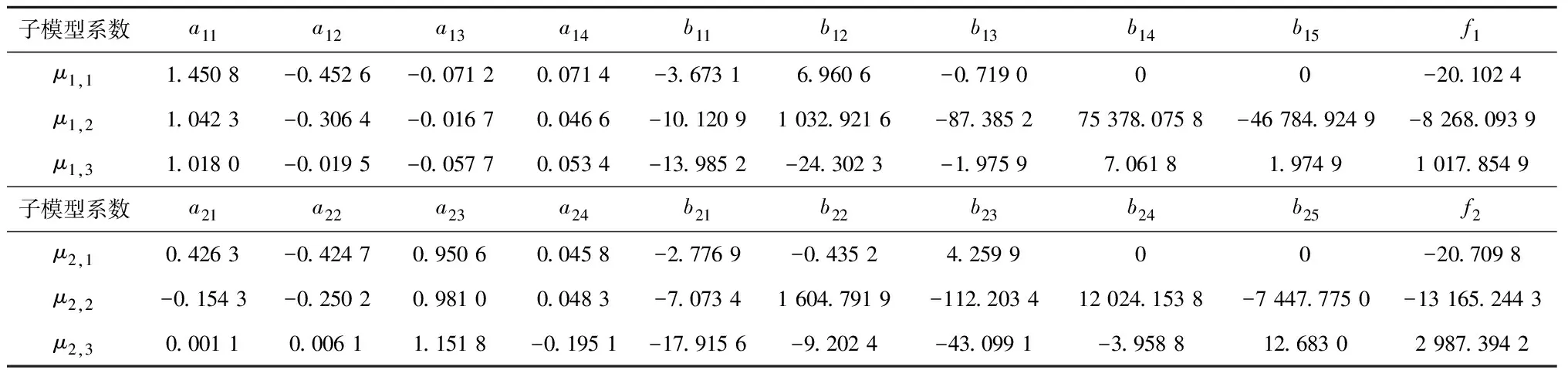
表3 模型辨识各项系数

表4 子模型边界超平面
(12)
3.4 模型验证及性能评价
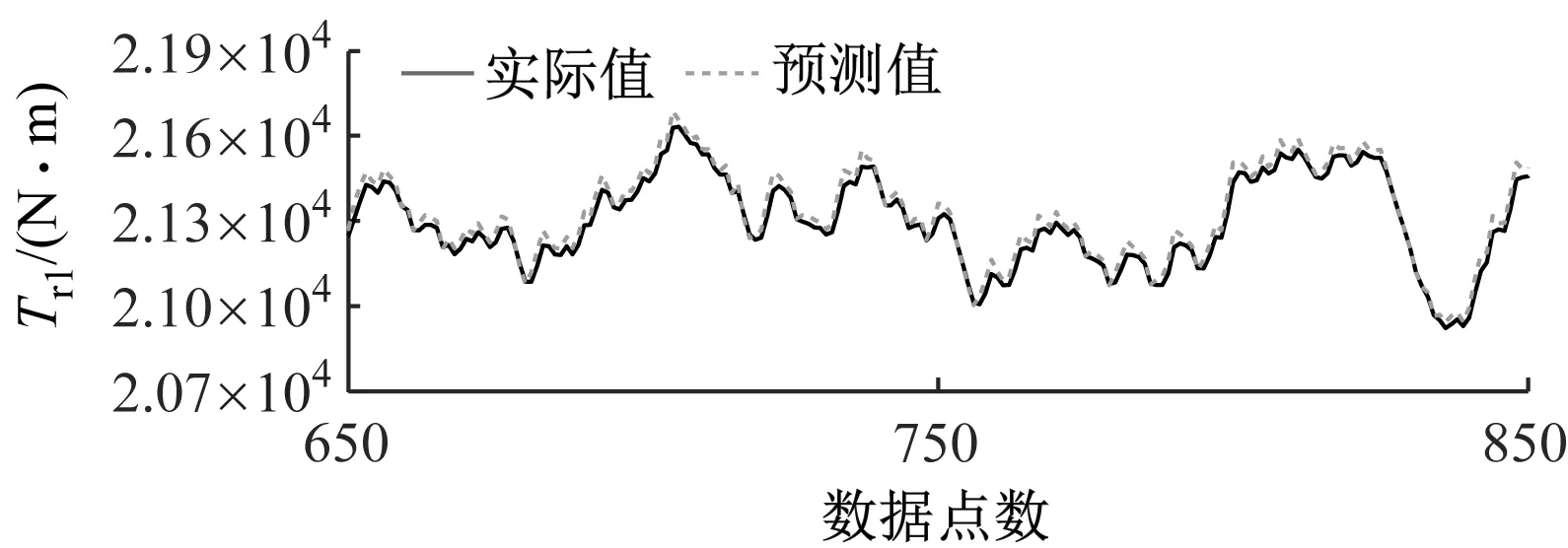
为验证所提PWARX模型精确度,采用所搭建的双风轮风电机组半物理仿真平台进行分析验证,根据平台生成不同工作域场景的运行数据来验证该模型的准确性和辨识精度,并对模型的误差进行评价。场景一、二分别为低、高风速2种单工作域运行场景,用于验证该模型单工作域子模型的预测效果;场景三为多工作域切换运行场景。各工作域场景生成的风速序列和PWARX模型在各场景下预测输出值和实际输出值的对比结果如图6~图14所示。
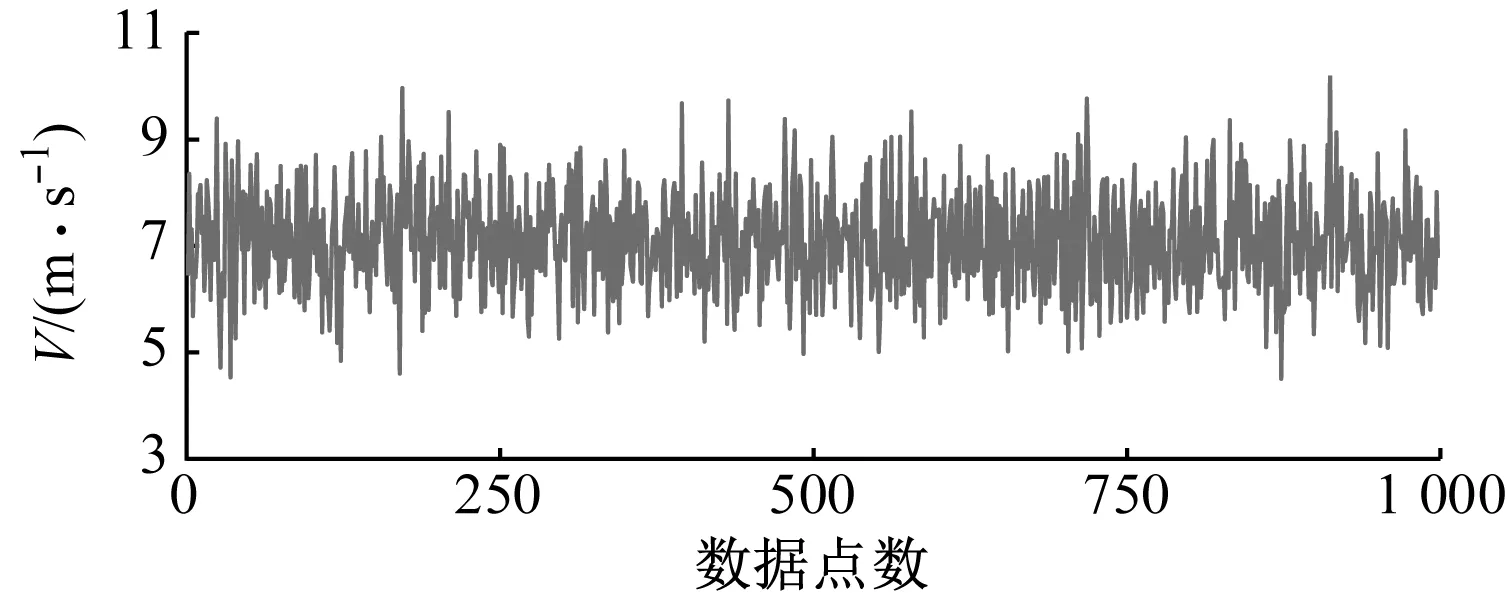
图6 场景一风速序列

(a) 前风轮
(a) 前风轮
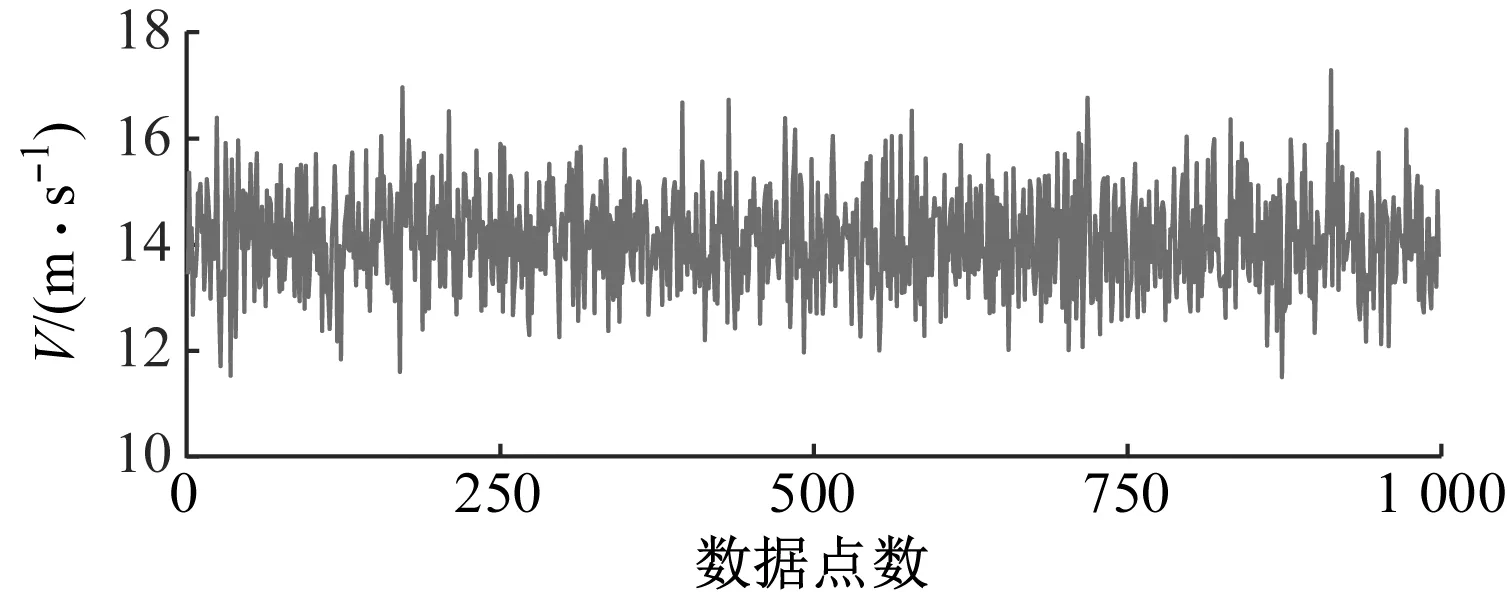
图9 场景二风速序列
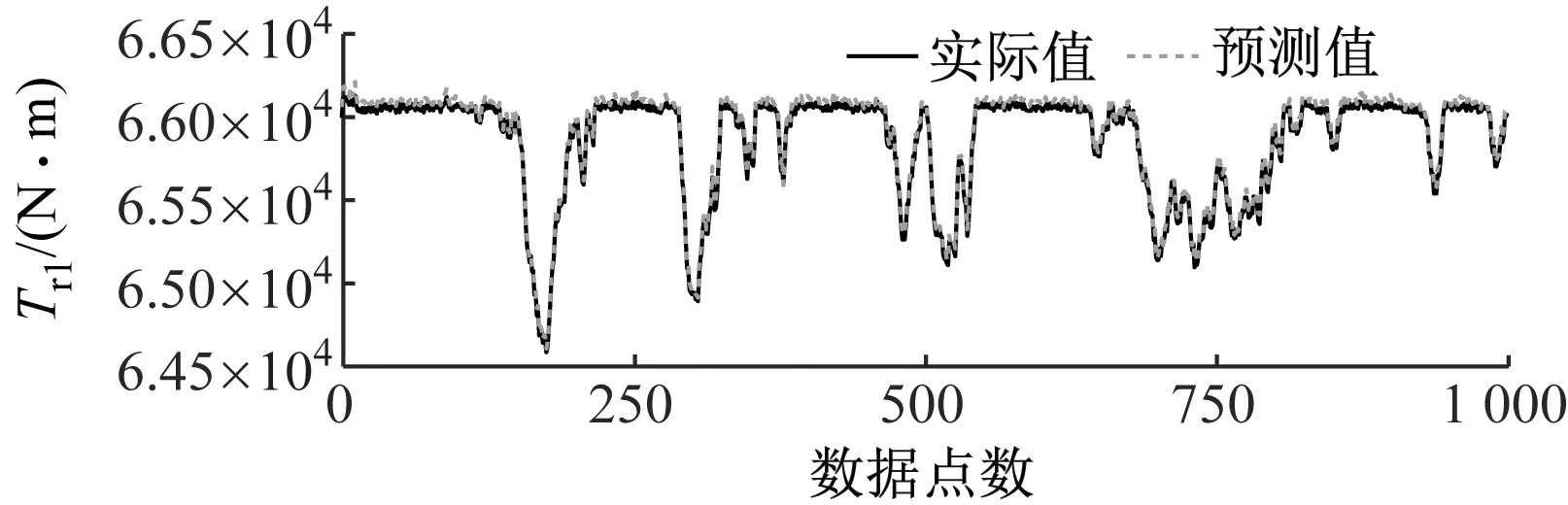
(a) 前风轮

(a) 前风轮
图12 场景三风速序列

(a) 前风轮
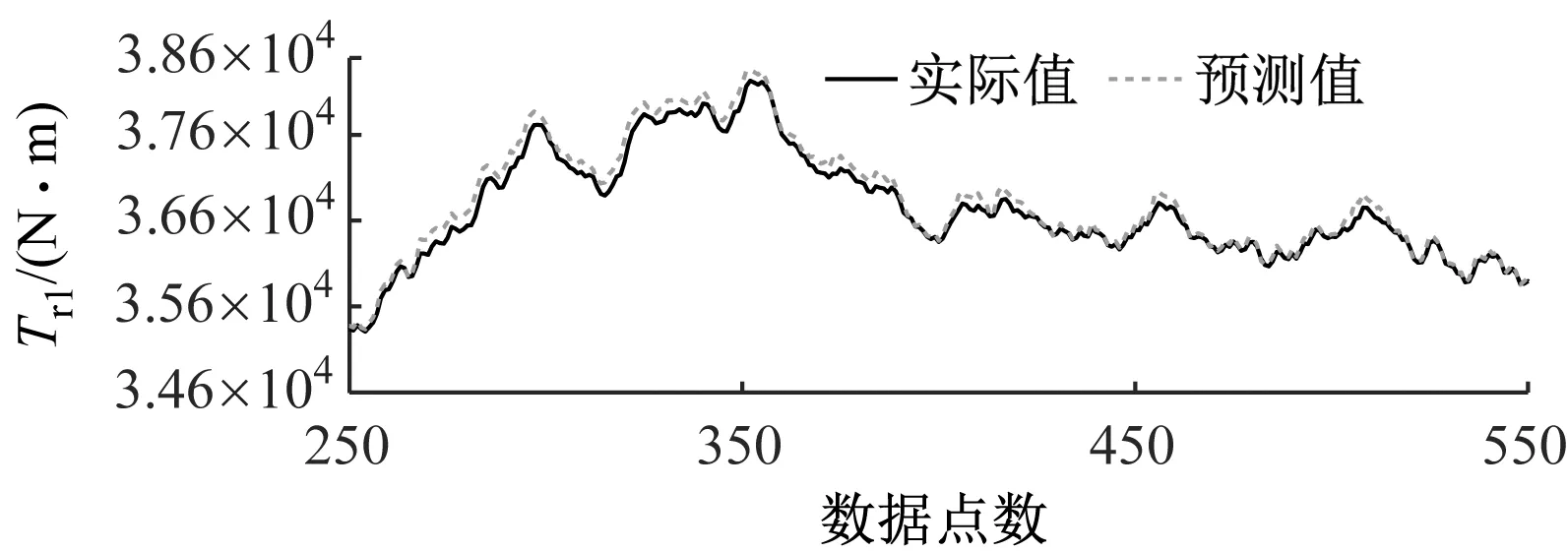
(a) 前风轮
单工作域场景模型性能指标见表5。由表5可知,模型应用在2种单工作域场景的前后风轮各性能指标相近,由于仅选取各单工作域1 000组数据,模型精度较高。

表5 单工作域模型性能指标
多工作域切换运行场景模型跟踪输出的精度较高,并且能克服工作域切换的扰动,以此类推达到多工作域子模型集成实现全工况动态逼近。多工作域模型评价指标见表6。由表6可知,模型在多工作域切换状态下也能保持良好的逼近性能,对实际输出有较好的跟踪性能。

表6 多工作域模型性能指标
综上所述,结合不同场景下的仿真验证情况,采用的双风轮风电机组气动MIMO系统全工况PWARX建模方案在不同场景下对输出实际值的拟合程度都没有出现较大的偏差,在不同场景下模型的输出值具有较好的逼近能力,都能很好地跟踪实际输出值的变化趋势,辨识参数准确度较高,对双风轮机组气动系统具有较好的拟合效果。
4 结 论
(1) 基于双风机气动子系统MIMO特性,提出基于高维空间聚类、超平面估计、有限差分作用域等概念建立双风轮风电机组气动MIMO系统全工况PWARX模型来估计实际输出气动转矩,表征双风轮气动系统的全局动态特性。
(2) 基于平台运行数据定义有限差分空间,划分作用域,适用于气动系统非线性问题。根据双风轮风电机组运行区间特性定义聚类个数相较于人为划分得到的聚类效果更好,工作域划分结果比较合理。
(3) 通过半物理仿真平台的双风轮风电机组模型设计实验和仿真验证,针对不同场景验证模型参数辨识结果的准确性。仿真结果表明,所提PWARX模型具有良好的区域动态表征能力,且其输出气动转矩能够较好地跟踪实际输出值,从而表明该方法的有效性。

