富水砂层水平旋喷拱棚的力学特性

陈焕然 石钰锋，2，3 陈昭阳 胡俊浩 朱江伟 王超

1.华东交通大学 江西省岩土工程基础设施安全与控制重点实验室， 南昌 330013； 2.江西省地下空间技术开发工程研究中心，南昌 330013； 3.华东交通大学江西建筑设计院有限公司， 南昌 330013； 4.合肥蜀山高科园区发展有限公司， 合肥 230088

水平旋喷预加固技术作为超前预支护手段之一，被广泛应用于地质情况复杂的隧道及其他地下工程。在富水砂层中开挖隧道时常采用拱棚加固，通过连续的水平旋喷桩（简称旋喷桩）加固土体并通过桩间咬合形成拱棚，保障围岩稳定的同时还有止水作用。

国内外学者对拱棚预支护技术进行了大量研究。试验研究方面，Nikbakhtan 等［1-2］对旋喷桩的力学特性进行了分析，得出旋喷桩的单轴抗压强度随着注浆压力增大呈指数型增长，黏聚力及摩擦角也随之增长，并统计了旋喷桩的物理力学参数。王超等［3］通过模型试验对富水砂层中拱棚的力学性能进行了研究，得出减小桩间距可以有效降低掌子面附近拱棚挠度。耿大新等［4］通过现场测试发现拱棚受力模式为掌子面前方和靠近洞口段受拉、掌子面后方受压，近似呈波浪形分布。理论分析方面，Flora 等［5］采用二维解析法得出拱棚的最优尺寸及最小厚度，并通过迭代程序对结构稳定性进行了验证。数值模拟方面，Mahdi等［6］对拱棚的硬化特性进行了研究，得出加固后的地层响应情况。石钰锋、赖金星等［7-8］通过建立三维模型验证了拱棚与大管棚复合超前支护能确保对地层的预加固效果，规避塌方风险。汪珂等［9］对有拱棚、无拱棚的工况进行模拟，得到两种工况下隧道结构变形规律。

上述研究主要是对具体工程的分析，没有对不同覆土厚度、地下水位等条件下拱棚力学特性的研究。数值模拟中大多不考虑地下水渗流作用、拱棚与土的接触效应以及开挖卸载对拱棚的影响。

本文通过模型试验和数值模拟进行富水砂层拱棚力学特性的研究，分析不同地下水位、地层渗透系数和覆土厚度对拱棚变形和受力的影响。

1 工程概况

江门隧道全长9 185 m，为双线单洞隧道。隧道外轮廓宽、高分别为11.9、11.6 m，采用台阶法开挖，开挖面积约120 m2。隧道主要穿越富水砂岩，裂隙发育，属Ⅵ级围岩。因隧道断面大、地下水丰富且沿线风险点较多，选用拱棚对地层进行预支护。支护角度为180°，旋喷桩的桩径、桩长和桩间距分别为0.50、25.00和0.35 m。隧道横断面及拱棚预支护见图1。

2 模型试验

2.1 试验装置及材料

为了研究拱棚在有、无地下水作用和开挖过程中的力学特性，制作了模型试验装置，见图2。箱体尺寸为1.74 m（长）×1.74 m（宽）×1.20 m（高），安装透明钢化玻璃以便于观察，设计了进水、出水系统并对箱体进行防渗处理。为了减小边界效应影响，填土前在箱体内壁满铺塑料薄膜，并在玻璃与薄膜之间涂刷润滑剂。

试验采用的几何、重度相似比分别为25.0、3.5。根据相似原理［10］，得到旋喷桩的桩径、桩长、桩间距分别为100.0、2.0、1.4 cm；拱棚弹性模量、重度、泊松比分别为137 MPa、5.5 kN/m3、0.25；拱棚采用水、石膏和硅藻土浇筑而成，其配比为3.2∶1.0∶0.4。选用赣江河砂来模拟砂层，其物理力学参数见表1。人工模拟开挖过程，两台阶开挖进尺均为4 cm。

2.2 测点布置

1）纵向测点。沿拱棚纵向布置应变、土压力和挠度测点，拱棚接缝两侧也各布置一组测点。应变片在拱棚迎、背土面对称布置，纵向间距为14 cm，每面布置5 列。土压力盒布置于拱棚迎土面，纵向间距为16 cm，布置2 列。挠度监测仪器布置于拱棚迎土面，布置方式与应变片相同，布置2列。

2）横向测点。沿拱棚横向布置应变和挠度测点。选择距离端部25 cm 处的横截面为监测断面，每类测点分别布置5 个，间隔角度分别为30°、45°、45°和30°。应变片在拱棚迎、背土面对称布置，挠度监测仪器布置于拱棚迎土面。

测点布置见图3。

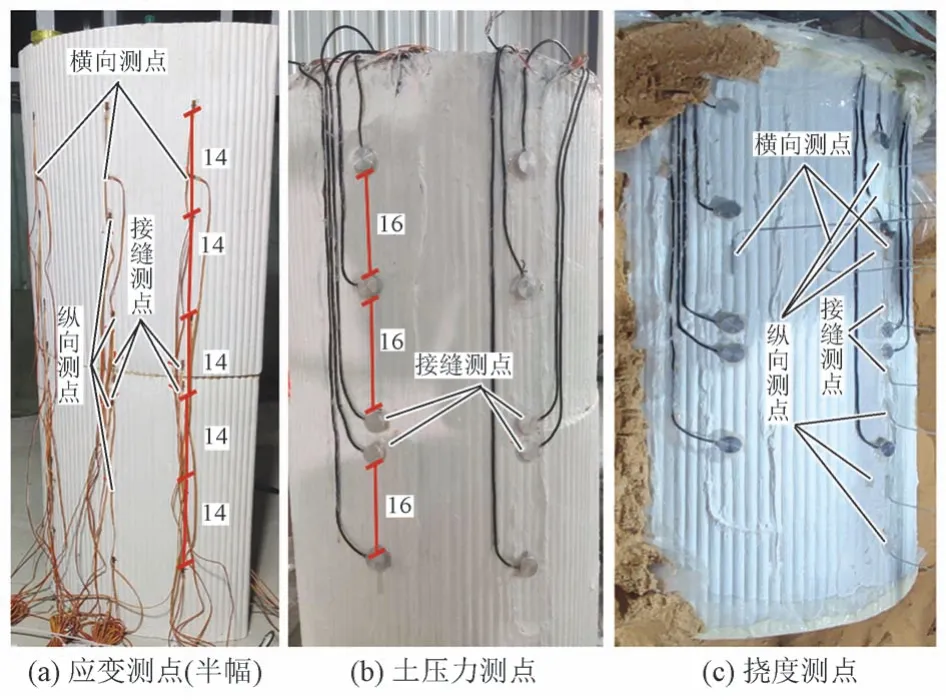
图3 测点布置（单位：cm）

2.3 试验结果

将试验结果通过相似关系换算成实际情况。覆土厚5 m，无水工况下不同上台阶开挖深度和上台阶开挖到18 m地下水位距拱顶0、2、4 m（低、中、高水位）时，拱棚挠度、轴力分布见图4。

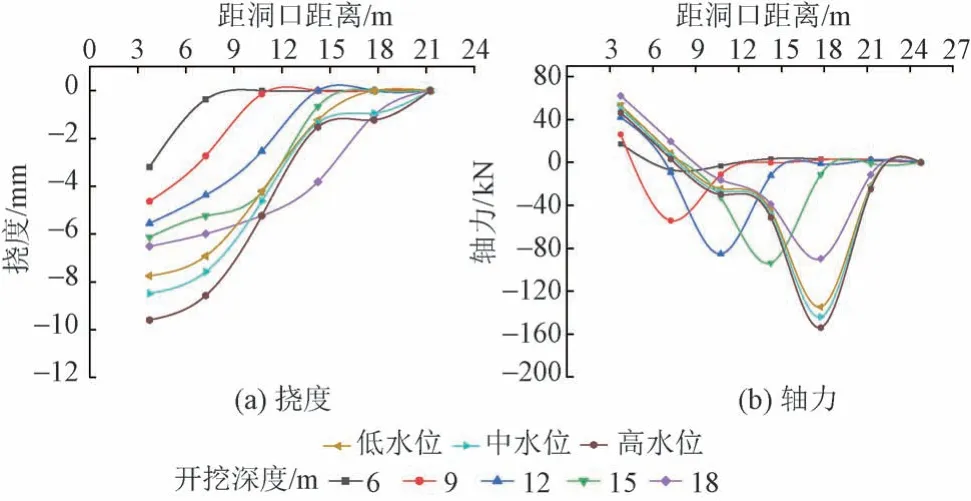
图4 拱棚挠度、轴力分布

由图4可知：

1）随着开挖深度增加，拱棚挠度增大；不同开挖深度下，越靠近洞口拱棚挠度越大。

2）隧道上台阶开挖到18 m 时，相比无水工况，①在远离掌子面（距离洞口小于10 m）位置，地下水的存在增大了拱棚挠度，且地下水位越高拱棚挠度越大；②在掌子面附近（距离洞口10～18 m）挠度曲线向上拱起，说明有地下水工况掌子面附近拱棚挠度比无水工况低，拱棚在富水砂层的预支护效果较好。

3）在掌子面附近，拱棚受压，有利于承载。

4）相比无水工况，地下水对洞口附近拱棚轴力影响较小；在掌子面附近，地下水位越高拱棚轴力越大。隧道上台阶开挖到18 m 时，与无水工况相比，高、中、低三种地下水位拱棚轴力增幅分别为19.14%、22.78%、26.57%。

3 数值模拟

江门隧道主要位于富水砂层，地下水非常丰富。数值模拟采用流固耦合的计算方法，分析多种工况下拱棚变形和受力情况。

3.1 模型建立及施工步骤

采用有限元软件建立三维模型，见图5。为减小边界效应的影响，模型尺寸取120 m（长）×50 m（宽）×80 m（高）。长度方向约为隧道宽度的10倍，隧道以下土层厚度约为隧道高度的5倍。采用上下台阶法模拟隧道开挖。

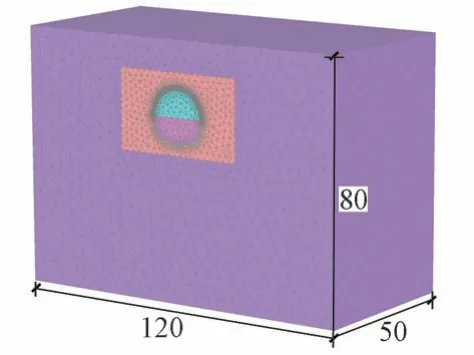
图5 计算模型（单位：m）

砂土、拱棚及初期支护均采用实体单元。砂土采用小应变土体硬化模型；拱棚及初期支护采用弹性模型，通过设定无限小的渗透系数来模拟材料的不透水性；拱棚与砂土间的接触效应采用界面单元模拟。

为了保证模拟结果准确可靠，拱棚、初期支护及砂土的物理力学参数与模型试验相同。拱棚的弹性模量、泊松比和重度分别为12 GPa、0.25 和19 kN/m3；初期支护的弹性模量、泊松比和重度分别为28 GPa、0.17和25 kN/m3。砂土物理力学参数见表2。

参考文献［11］，数值模拟的步骤为：①地应力平衡计算，完成后施作拱棚；②隧道上台阶开挖，围岩应力释放30%；③施作上台阶初期支护，围岩应力释放70%；④隧道下台阶开挖，围岩应力释放100%；⑤施作下台阶初期支护；⑥重复步骤②—⑤。上述每步骤完成时间均为2 d。

3.2 模型验证

拱棚与砂土间界面单元的强度折减系数（Rinter）对数值模拟的可靠性有重要影响。根据单一变量原则，计算隧道上台阶开挖深度为9 m，Rinter分别取0.85、0.80、0.75、0.70、0.65、0.60、0.55、0.50、0.45、0.40时拱顶位置拱棚挠度和轴力，并与模型试验结果进行对比，见图6。

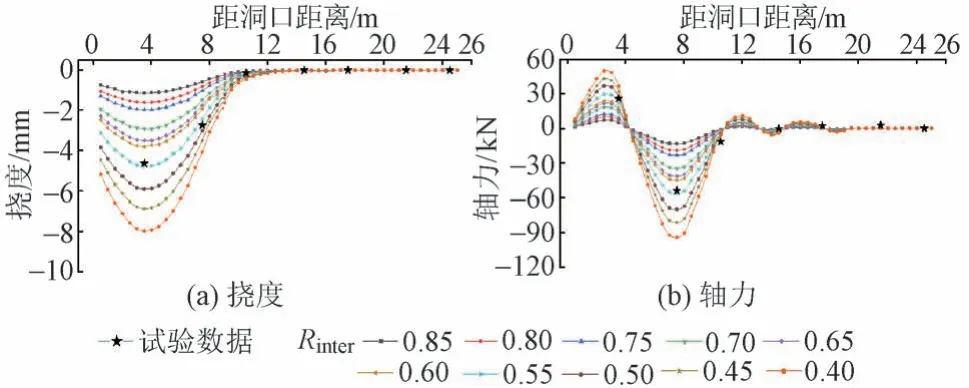
图6 拱顶位置拱棚挠度和轴力模拟值和试验值对比

由图6可知：当Rinter为0.55时，数值模拟结果与模型试验结果最接近，且曲线分布规律基本一致。因此设定Rinter为0.55。

3.3 模拟工况设计

参考文献［12］，分析不同地层渗透系数、覆土厚度和地下水位条件下，当隧道开挖到9.5 m 时拱棚挠度和轴力。各工况见表3。

表3 模拟工况

拱棚监测点共选择5 处，分别位于距离洞口8、9、10、11、12 m的拱顶位置，命名为测点1#—5#。

3.4 计算结果分析

3.4.1 地层渗透系数对拱棚力学特性的影响

不同地层渗透系数条件下拱棚挠度和轴力曲线见图7。可知：①地层渗透系数越小，拱棚挠度和轴力越大；②与地层渗透系数的变化率相比，拱棚挠度和轴力变化率均很小，可见地层渗透系数对拱棚受力影响较小。

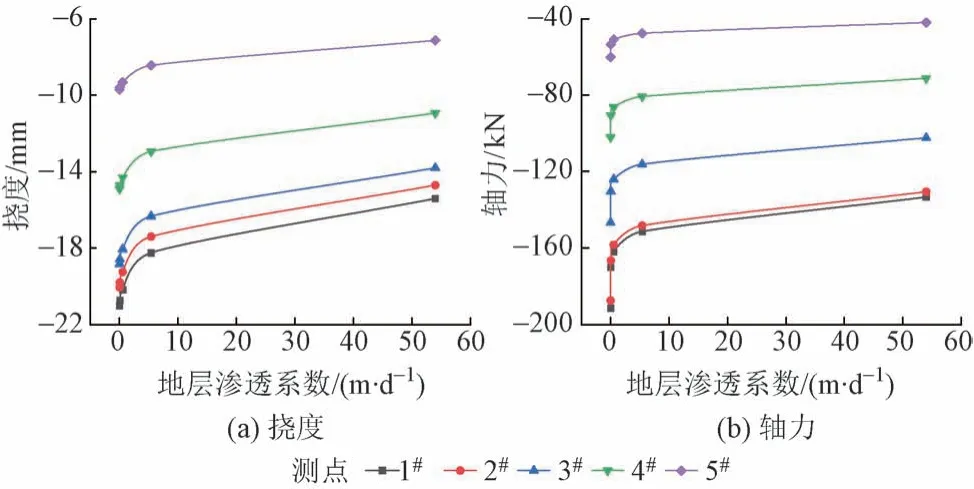
图7 不同地层渗透系数条件下拱棚挠度和轴力曲线

3.4.2 覆土厚度对拱棚力学特性的影响

不同覆土厚度条件下拱棚挠度和轴力曲线见图8。可知：①随着覆土厚度增加，拱棚挠度和轴力均增加。②在掌子面附近（测点2#），相比覆土厚5 m 工况，随着覆土厚度增至7、9、11、13 m 时，拱棚挠度分别增长12.69%、21.98%、36.66%、44.76%，轴力分别增长15.02%、36.71%、52.07%、73.25%，均近似呈线性增长。

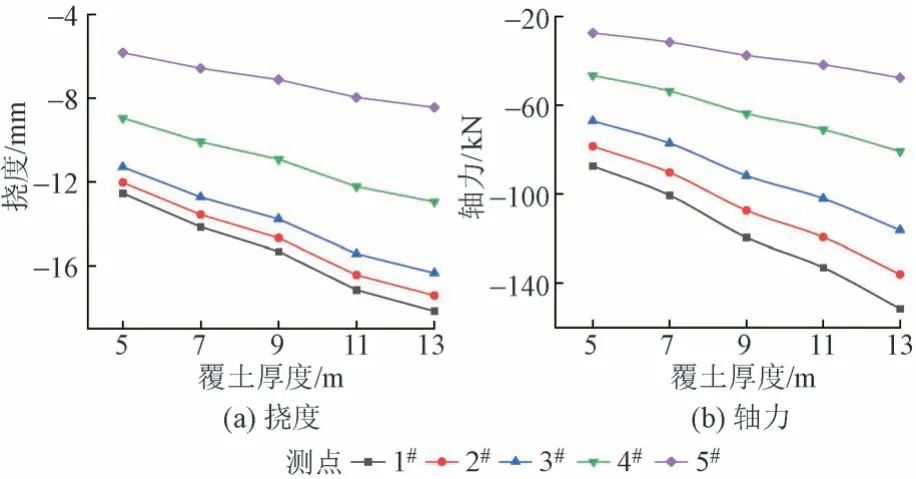
图8 不同覆土厚度条件下拱棚挠度和轴力曲线

3.4.3 地下水位对拱棚力学特性的影响

不同地下水位条件下拱棚挠度和轴力曲线见图9。可知：①地下水位越低，拱棚挠度和轴力越小；地下水位位于拱顶时，拱棚挠度和轴力最小。②在掌子面附近（测点2#），相比于地下水位位于拱顶工况，随着地下水位升至距拱顶1、2、3、4、5 m 时，拱棚挠度分别增长6.41%、13.78%、24.51%、35.83%、47.65%，近似呈线性增长。③当地下水位较低时（距拱顶0 ～3 m），拱棚轴力随着水位升高近似呈线性增长；当水位较高（距拱顶大于3 m）时，随着水位升高轴力增速变大；可见地下水位对拱棚轴力影响较大，为保证隧道施工安全，可先采取降水措施以减小拱棚受力。

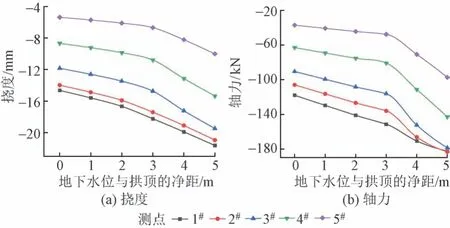
图9 不同地下水位条件下拱棚挠度和轴力曲线

4 结论

本文以江门隧道工程为依托，通过模型试验和数值模拟分析了在富水砂层中拱棚的力学特性。

模型试验结果表明：①随着开挖深度增加，拱棚挠度增大，越靠近洞口拱棚挠度越大。②有地下水工况掌子面附近拱棚挠度比无水工况低，说明拱棚在富水砂层的预支护效果较好。③掌子面附近拱棚受压，且拱棚压力最大值位于此处。④相比无水工况，地下水位对洞口附近拱棚轴力影响较小；在掌子面附近，地下水位越高拱棚轴力越大。

数值模拟结果表明：①地层渗透系数对拱棚挠度和轴力影响最小。②覆土厚度小于13 m、地下水位与拱顶净距3 m 时，随着覆土增加拱棚挠度和轴力近似呈线性增长。③覆土厚13 m 时，随着地下水位升高拱棚挠度和轴力增大；当地下水位与拱顶净距大于3 m后，随着水位升高轴力增速变大；地下水位对拱棚受力影响较大，为保证隧道施工安全，建议采取降水措施减小拱棚受力。