水/石墨烯界面离子吸附的分子动力学模拟: 力场参数优化与吸附机制

廖首维， 刘炎昌， 石泽南， 赵道辉， 魏嫣莹，3， 李理波，3

（1. 华南理工大学化学与化工学院, 广东省绿色化学产品技术重点实验室, 广州 510640；2. 湖北大学化学与化工学院, 武汉 430062； 3. 华南理工大学制浆造纸工程国家重点实验室, 广州 510640）

石墨烯、 二硫化钼和Mxene等二维材料［1～3］构建的纳米孔道在离子输运与筛分、 水输运等方面表现出大量的新颖现象和优异性能［4～8］， 因而在许多领域（如海水淡化［5，9～13］、 渗透发电［14～17］、 超级电容器［18～20］、 纳米元器件［21，22］等）具有广阔的应用前景. 与之相关的研究往往涉及盐溶液-二维材料体系， 时空尺度很微小， 通常的实验技术难以灵敏检测［23］.

量子化学需要的计算资源太多， 通常只能模拟数百原子、 数百皮秒的时空尺度［24］； 传统连续介质模型精度不够高， 很难准确描述1 nm以下的尺度［25，26］： 它们都很难用于盐溶液-二维材料体系的研究.经典分子动力学（Molecular dynamics， MD）模拟因其处理的时空尺度合适（显著大于量子化学计算）、 模拟精度较高（显著高于连续介质模型）， 已被广泛应用于各种盐溶液-二维材料体系［20，27～31］的研究， 为实验研究提供越来越重要的指导和补充作用.

目前， 用MD模拟研究二维材料纳米孔道里盐溶液面临的主要问题有： 首先， 石墨烯等金属、 半导体二维材料与离子之间存在强烈的离子-π相互作用［32～37］. 最近的模拟［38］和实验研究［9，37］都表明， 离子-π相互作用对离子在石墨烯纳米孔道里的吸附与输运很重要， 然而当前的固定电荷力场（Fixed charge force field）设定石墨烯C原子电荷为0（因为各C原子化学环境相同）， 无法体现离子-π相互作用引起的电荷变化， 导致无法模拟离子在石墨烯表面的吸附. 从头算分子动力学（AIMD）［39］可模拟的时空尺度太小； 可极化力场MD模拟［35］的运算速度也很慢， 且该方法还在继续发展中. 而MD模拟力场中不同原子之间的Lennard-Jones（LJ）作用参数往往使用混合规则（如Lorentz-Berthelot 或LB 规则）计算得到， 也难以描述离子-π相互作用. 根据相关实验数据［40］或量子化学计算结果［41］优化LJ作用参数， 是提高力场准确性的一个有效途径， 已被广泛用于改进各类体系［烷烃-水［42，43］、 离子-氨基酸［44，45］、 水-石墨烯［40，46，47］、 气体-金属有机框架材料（MOFs）［48］等］的力场参数. 用此策略发展离子-石墨烯作用参数， 可望在保持MD快速、 可模拟较大时空尺度优点的同时， 准确描述离子-π作用， 大大提高其模拟石墨烯纳米孔道［39，49］的准确度. 其次， 石墨烯等二维材料与溶液中离子相互作用的热力学机制， 尤其是溶剂对离子在材料表面吸附的调控作用目前还缺乏深入研究. 如， 水吸附在石墨烯表面形成密度较高的水层， 对水分子的氢键数、 居留时间都会产生重要影响， 这已得到深入研究［40，46］； 但该水层结构对离子吸附的影响还少有报道. 这些问题都限制了二维纳米孔道离子输运的研究［7，50］和相关纳米器件的开发［51］.

本文以石墨烯这一有代表性的（半）金属二维材料为例， 在Merz团队［52，53］以及Netz团队［54，55］开发的离子力场参数（分别称为Merz力场和Netz力场）的基础上， 优化了Li+， Na+， K+， Mg2+， Ca2+和Cl-离子与石墨烯相互作用的LJi-C参数. 优化参数模拟得到的离子-石墨烯吸附自由能（若无特别说明， 只研究溶液中的体系）与量子化学计算结果一致［38］， 可准确描述（溶液中）石墨烯-离子之间的离子-π相互作用；还将（溶液中）离子在石墨烯表面吸附的平均力势［56］（PMFads）分解为石墨烯-离子、 水-离子等相互作用的贡献（简称PMFgra和PMFwat）； 在此基础上研究了石墨烯表面溶剂结构对离子吸附的调控机制； 进一步模拟了实际浓度下各种盐溶液/石墨烯界面， 比较了优化前后LJi-c参数对模拟结果的影响， 以及这些界面上离子浓度分布与PMFads和离子间相互作用之间的关系.

1 模型与方法

1.1 模拟系统

模拟了两种不同类型的体系： 含1个离子的水/石墨烯界面体系［用于计算PMFads， 图1（A）］和盐溶液/石墨烯界面体系［研究离子的界面行为， 图1（B）］.

Fig. 1 Simulation system of single ion + graphene in aqueous solution(A) and 1 mol/L salt solution/graphene interface(B)

1.1.1 水/石墨烯界面的单离子 通过伞形采样［57］模拟计算（水中）离子在石墨烯表面吸附的PMFads曲线. 如图1（A）所示， 一个离子位于C54H18石墨烯薄片（碳、 氢原子均被固定）的中央位置上方， 将其置于含有1351个水分子的模拟体系（尺寸为3.5 nm×3.5 nm×3.5 nm）. 为了计算PMFads， 需要进行14个独立的模拟； 每个模拟的离子与石墨烯的垂直（z方向）距离为0.2～1.5 nm（间隔0.1 nm， 各模拟窗口的采样充分重叠， 表明结果可靠， 见本文支持信息图S1）.

在x，y和z方向对离子施加力常数为1000 kJ·mol-1·nm-2的简谐势以限制离子在特定位置附近运动：x，y方向简谐势使离子保持在石墨烯中心，z方向简谐势用于伞形采样. 在正则（NVT）系综中进行20 ns的伞形采样模拟， 后10 ns模拟轨迹使用加权直方图分析方法（WHAM）［58］计算PMFads曲线. 若无特别说明， PMF计算均采用碳、 氢原子电荷为0［与图1（B）体系的原子电荷一致］的C54H18石墨烯片， 体系仅放置单个离子（无抗衡离子， 这是模拟无限稀释盐溶液的通常做法［59］）. 选取PMFads达到收敛且保持不变时的势能（距离石墨烯大于1.2 nm）作为零势能参考面， 取PMFads曲线的最小值［38］（图S2， 见本文支持信息）为溶液中离子-石墨烯吸附能（Eads）. PMFads的形状及其最小值（吸附自由能Eads）均随LJi-C参数（εi-C）参数的不同而改变（图S2）， 通过调整εi-C参数， 使得MD模拟得到的Eads与量子化学方法计算的水/石墨烯界面的离子吸附能（EQCads， 取自文献［38］）一致， 从而获得优化后的参数εion-πi-C（表1）， 参数εi-C优化过程见本文支持信息的S1节.

1.1.2 盐溶液/石墨烯界面 如图1（B）所示， 1 mol/L的LiCl， NaCl， KCl， CaCl2或MgCl2盐溶液（含30个阳离子与相应数量的Cl-离子， 模拟体系净电荷为0）与尺寸3.69 nm×3.843 nm的单层石墨烯（540个碳原子， 电荷设为0［38，46］，z坐标为0）接触， 置于3.69 nm×3.843 nm×7 nm的模拟盒子. 盐溶液的厚度约为3.5 nm（含1324个水分子）， 溶液上方有高度约3.5 nm（模拟盒子高度7 nm）的真空间隙以消除周期性对模拟结果的影响. 各盐溶液/石墨烯界面体系在NVT系综中模拟20 ns， 采用后10 ns的模拟轨迹进行分析.

Table 1 LJi-C parameters and adsorption energy of ion-graphene simulated with Merz and Netz force fields

1.2 模拟设置

采用LJ 势和静电势计算分子间相互作用； 离子与石墨烯的碳原子之间的LJ 相互作用为V(r)=（其中，εi-C和σi-C是LJi-C参数）， 通常利用LB 混合规则得到［εLi-BC=(εi·εC)12，σLBi-C=(σi+σC)/2］.

主要基于量子化学计算的（水中）离子在石墨烯表面的吸附自由能Eads［38］优化得到离子-碳相互作用强度参数εion-πi-C（Eads计算方法与εion-πi-C优化方法见1.1.1节与支持信息的S1节， 若不特别说明，Eads均指在水中的吸附自由能）； 而σi-C参数在优化前后保持不变（均为σLBi-C）.

分别采用Merz力场［52，53］和Netz力场［54，55］对离子进行模拟； 采用刚性石墨烯模型［石墨烯原子（包括封端的氢原子）的位置均被固定， 这也是石墨烯MD 模拟研究的通常做法［60，61］］， 碳原子力场参数（εC=0.4899 kJ/mol，σC=0.3214 nm）取自Werder 等［62］的工作； 使用拓展简单点电荷（SPC/E）水模型［63］. 水、离子以及石墨烯的LJ参数及原子电荷见表S1（本文支持信息）. 如无特别说明， C54H18的C和H原子电荷均为0； 还计算了C54H18的限制性拟合静电势（RESP）原子电荷［64，65］， 但原子电荷对PMF的影响很小，见本文支持信息S2节.

使用GROMACS 5.0.5 软件［66］进行MD 模拟， 使用VMD 软件［67］进行可视化. MD 模拟轨迹采用蛙跳算法进行积分， 时间步长为2 fs. 图1模拟系统的x，y和z方向都应用了周期性边界条件. 在所有模拟中，分子间LJ相互作用的截断距离为1.2 nm，

采用Particle mesh Ewald 方法［68］计算长程静电相互作用. 使用SETTLE 算法［69］约束水分子的键长. 使用Nose-Hoover方法［70～72］控温， 耦合温度为298.15 K. 图1（A）体系先在NPT系综进行5 ns的预平衡模拟（使用Parrinello-Rahman 方法［72～74］控压， 耦合压力为1×105Pa）， 之后在NVT 系综中进行模拟；图1（B）的体系使用NVT系综进行模拟.

2 结果与讨论

2.1 离子-石墨烯相互作用参数的优化与离子在水/石墨烯界面的PMFads曲线

研究了Merz和Netz这两个团队分别开发的Li+， Na+和K+等离子力场参数（简称Merz力场［52，53］、 Netz力场［54，55］， 将未经过优化的力场参数简称为“优化前”力场）. 在这两套力场参数的基础上分别优化了离子-石墨烯的作用参数（简称为“优化后”力场）： 这些优化前后的参数， 及由其计算得到的（溶液中）离子在石墨烯表面的吸附自由能Eads见表1.

使用优化后力场参数（εiio-nC-π）计算得到的Ead（s绝对值）均比优化前力场参数（εLi-BC）计算得到的结果更大， 且与量子化学计算结果（EQCads）［38］一致. 在此基础上， 测试了石墨烯片的尺寸大小（图S3， 见本文支持信息）、 原子电荷（图S4， 见本文支持信息）以及抗衡离子（图S5， 见本文支持信息）等可能影响参数优化的模拟条件（S2节）， 并计算相应的PMFads曲线（以Na+为例， 使用Merz力场优化前、 后的参数）.

上述模拟条件的改变对PMFads曲线的影响都很微弱， 对于C54H18或更大尺寸的石墨烯片， 伞形采样模拟的Eads与量子化学计算的EQCads都基本不变且二者一致［图S3（A）］， 验证了本文PMFads计算体系的合理性. 结果表明优化后εion-πi-C参数可准确描述溶液中离子-石墨烯之间的离子-π相互作用.

无论用εLBi-C或εion-πi-C参数模拟得到水/石墨烯界面处离子的PMFads曲线（图2）， 当各离子距离石墨烯z＞ 1.2 nm时， 它们的PMFads都很接近0， 表明此时离子-石墨烯相互作用十分微弱； 当z＜1.2 nm， PMFads开始剧烈波动并产生多个极大值和极小值， 用εLBi-C或εion-πi-C参数计算的PMFads存在明显差异. 当0.3 nm＜z＜1.2 nm，εLBi-C参数的PMFads基本都大于0（即离子接近石墨烯时能量上升）， 且PMFads的最小值距离石墨烯较远（z＞0.5 nm）， 表明离子不会吸附在石墨烯表面. 这是因为石墨烯的空间位阻导致离子水合层变形甚至脱水［40，75］（图3）， 使PMFads上升的作用处于主导地位（εLBi-C参数未考虑离子-π作用， 模拟的离子-石墨烯相互作用较弱）. 唯一的例外是Li+离子，εLBi-C参数的PMFads在石墨烯表面（z＜ 0.5 nm）仍然存在最小值， 但阱深并不深， 与z≈0.75 nm的极小值接近（表1）.

Fig.2 PMFads for Li+(A), Na+(B), K+(C), Ca2+(D), Mg2+(E) and Cl-(F) ions adsorbed at the water/graphene interface

相反，εiio-nC-π参数的PMFads都比的更低，z＜1.0 nm 时一般都小于0（仅Li+的个别距离区间里，PMFads为很小的正数）， 这是因为εiio-nC-π参数可准确描述离子-π相互作用， 模拟的离子-石墨烯相互作用较强， 使PMFads下降的趋势居主导地位. 当离子紧密接触石墨烯时（z＜0.3 nm）， 无论模拟采用还是εiio-nC-π参数， 离子的第一和第二水合层都由于石墨烯的空间位阻而脱水（图3）， 同时， 石墨烯与离子之间存在LJ势能斥力， 因此PMFads曲线均随z减小而急剧上升.

Fig.3 Relationship between ion-graphene distance and coordination numbers for the first(circle)and second(squares) hydration shells(denoted as Nw1 and Nw2, respectively) for Li+(A), Na+(B),K+(C), Mg2+(D), Ca2+(E) and Cl-(F)

2.2 离子-水和离子-石墨烯相互作用对PMFads曲线的影响

为了进一步研究离子-石墨烯作用和离子-水作用对PMFads的贡献， 模拟了以下两种不同体系：（1） 真空中离子+石墨烯［去除图1（A）体系的水分子， 其它保持不变］， 离子位于石墨烯正中央的上方；（2） 与图1（A）模拟体系一致， 但模拟时不计算离子-石墨烯作用（设置εi-C=0 kJ/mol）. 在这两种体系中，离子分别受石墨烯或水相互作用， 模拟得到的PMF 分别称之为PMFgra或PMFwat（图4）， 且PMFads=PMFgra+PMFwat［图S6（见本文支持信息）， 将PMF分解为模拟各组分贡献的做法已有研究报道［76，77］， 表明其准确性］. PMFgra的形状比较简单， 随着离子接近石墨烯， PMFgra单调下降，z≈0.3 nm（约等于σi-C，表1）时达到极小值（数值与εi-C成正比， 见图S7， 见本文支持信息）， 之后， 由于C原子-离子之间的排斥作用急剧上升. 实际上， PMFgra与离子-石墨烯相互作用的LJ势能曲线一致（图S8， 见本文支持信息）.与之相反， PMFwat的形状复杂很多， 当离子距离石墨烯比较远时（z＞1.2 nm）， 此时水可视为各向同性的均匀介质， PMFwat是常数. 当接近石墨烯时（z＜1.2 nm）， 一方面水在石墨烯表面形成了两个密度较高的水层［32］［图5（A）］， 这两层水与离子的作用不同于体相水； 另一方面离子的水合层结构及水合数均开始变化［33］（图3、 图5和图6）. 这两方面的作用使得PMFwat有复杂的变化.

由于离子接近石墨烯时水合层结构发生变化（图3）， PMFwat从z＜1 nm开始总体趋势都向上且基本大于0（图4）； 但阳离子的PMFwat仍存在两个极小值（Na+， K+也存在两个极小值， 虽较不明显， 图4）. 且可见， 阳离子PMFwat极小值的位置与石墨烯表面两层水的位置［32］存在对应关系［图5（A）］： 第一极小值（z=0.3～0.55 nm）位于第一、 第二水层之间； 第二极小值（z=0.7～0.8 nm）位于第二水层之外（远离石墨烯）. 另外， 离子第一、 第二水合层开始脱水时的位置（见本文支持信息表S2， 即水合数开始变化的位置； 以下分别称为“第一水合层拐点”和“第二水合层拐点”）分别与PMFwat第一、 第二极小值的位置一致［图5（B）］. 以上水层位置、 PMFwat极小值位置和水合层拐点之间的关联表明， PMFwat的极小值和极大值可能是离子-水层相互作用和脱水作用两个因素共同导致. 进一步计算Li+离子在PMFwat的极小值和极大值位置时， 离子周围的水密度分布（图6， 其它阳离子接近石墨烯时， 周围水相对密度分布变化类似）.

Fig.4 PMFads, PMFgra(contribution of ion-graphene interactions to PMFads) and PMFwat(contribution of ion-water interactions to PMFads) for Li+(A), Na+(B), K+(C), Ca2+(D), Mg2+(E) and Cl-(F) ions adsorbed at the water/graphene interface

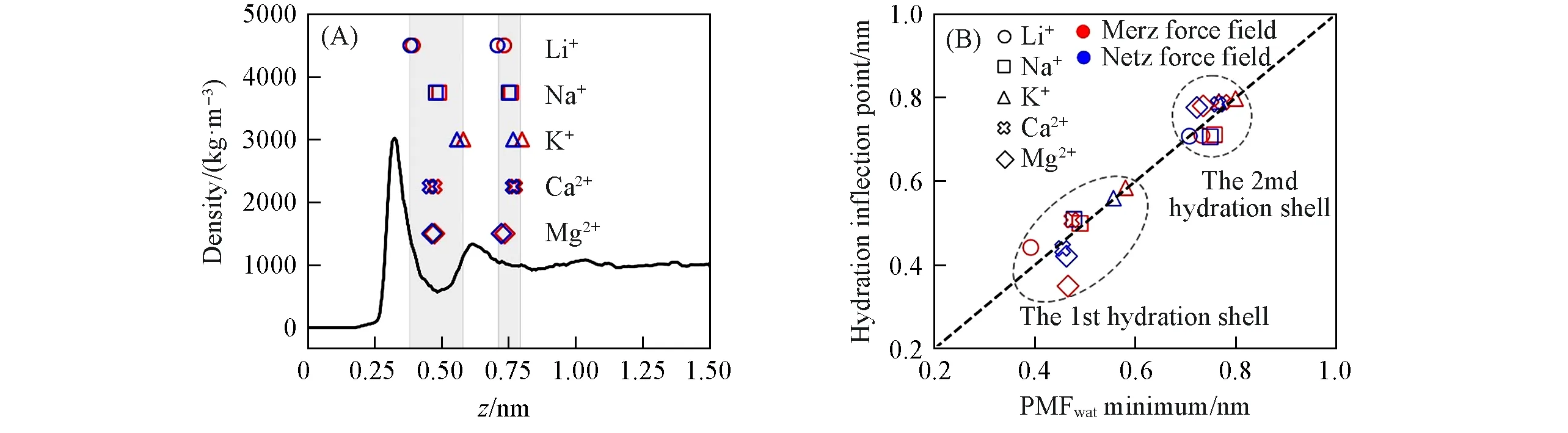
Fig.5 Water density distribution above graphene flake(black curve) and the positions of cation PMFwat’s minimum(A), PMFwat’s 1st and 2nd minimum positions agree with corresponding hydration inflection points’ position(B)

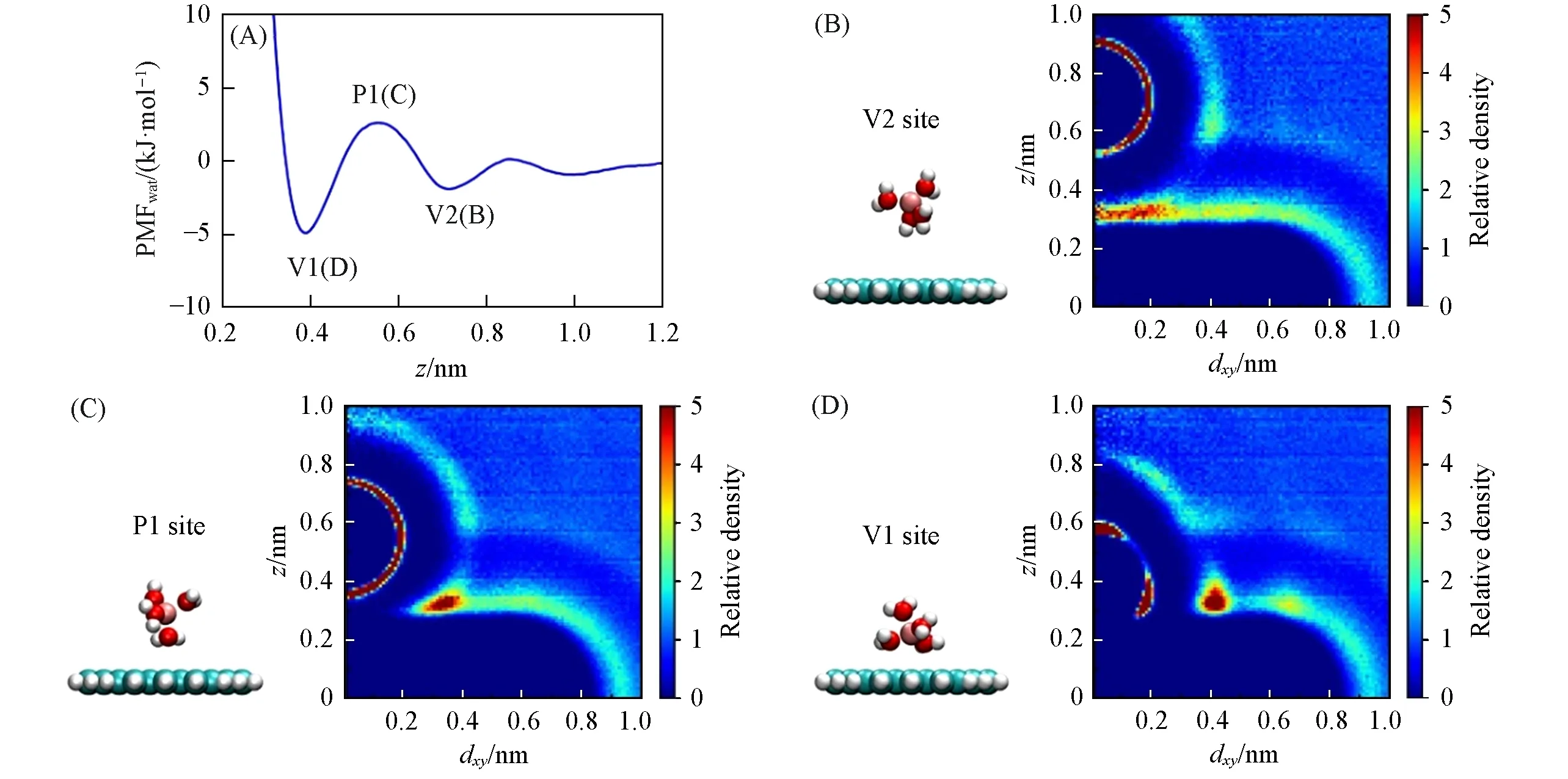
Fig.6 PMFwat of Netz force field’s Li+(P1, V1, V2 represent the 1st maximum, the 1st and 2nd minima, respectively)(A), corresponding snapshots of the ion’s 1st hydration shell and the relative density distribution of water(B—D)

为了简便， 分别用P1， V1 和V2 表示PMFwat的第一极大值和第一、 第二极小值［图6（A）］. 当离子接近第二水层［z≈0.6 nm， 图5（A）］， 因水层的水密度较高， 离子第二水合层水合数甚至略有上升［图3（A）， 由图6（B）可见， 第二水合层与石墨烯表面水层相交处的水密度增大］， PMFwat开始下降； 当离子到达V2位置［与第二水合层拐点一致， 图5（B）］， 第二水合层开始脱水（图3）， 因水合层脱水造成的能量惩罚（若水合层全部脱去， 其能量惩罚即离子的水合能）使得PMFwat上升， 故此时PMFwat达到一个极小值. 随着离子进一步接近石墨烯（z=0.4～0.55 nm）， 石墨烯表面第一水层与离子距离接近［图6（C）］， 相互作用强烈， 故PMFwat又开始下降并在P1位置产生极大值. 离子在z=0.4～0.6 nm时处于两层水中间， 同时与它们作用［图5（A）和图6（D）］， 能量相当有利； 而再进一步接近石墨烯时， 离子的第一水合层开始脱水（图3， 除了Netz力场的Li+）， 使得PMFwat急剧上升（因为离子第一水合层与离子结合更紧密， 所以PMFwat上升更加剧烈）， 故PMFwat在V1位置达到另一个极小值. 进一步可见， 各离子的第一水合半径［离子-（水）氧原子径向分布函数的第一极小值位置， 图S9， 见本文支持信息］与水合层拐点有明显关联： 水合半径大的离子， 水合层拐点的位置距离石墨烯也更远［图S10（A）， 见本文支持信息］. 换言之， 水合半径小的离子需要更接近石墨烯， 其水合层才开始脱水.

离子第二水合层的情况比第一水合层更复杂， 所以第二水合层拐点与第二水合半径的关联较弱［图S10（B）］. 这些结果说明， 离子接近石墨烯时， 一方面离子受到石墨烯表面两个水层作用， 使PMFwat降低； 另一方面由于离子第一、 二水合层变形甚至脱水使PMFwat升高. 后者一般主导， 使得PMFwat在z＜1 nm 时呈上升趋势， 一般大于0； 而有时前者也可占主导地位. 因此不同阳离子的PMFwat在z=1 nm以内都呈现出一个极大值和两个极小值； 进一步接近石墨烯（z＜0.3 nm）时， PMFwat因离子强烈的脱水作用而急剧上升. 与阳离子相反， 随着Cl-接近石墨烯， Cl-的PMFwat呈现从水平到单调上升的趋势［图4（F）］： 在第一和第二水合层拐点之间的区域（z=0.6～0.7 nm， 表S1）， Cl-的PMFwat基本不变， 因为此时Cl-与石墨烯表面水层相互作用的PMFwat下降趋势与第二水合层脱水的上升趋势相互抵消； 而到达第一水合层拐点之后（z＜ 0.6 nm）， 脱水作用起主导作用， PMFwat上升.

使用εLBi-C模拟时， 各阳离子的PMFads与它们的PMFwat都很接近（图S11， 见本文支持信息）. 在各阳离子PMFads的第一极小值之外， 其PMFgra基本为0， 且PMFgra势阱较小无法抵消PMFwat的上升， 所以PMFads与PMFwat很接近. 反之， 使用εion-πi-C模拟时（图4）， 由于离子-石墨烯作用强烈， PMFgra不可忽略， 显著影响了PMFads最小值的大小甚至位置（离子-石墨烯距离）， 因此各离子的PMFads都与PMFwat差距明显. 进一步发现， Li+， Mg2+和Ca2+离子的PMFads最小值位置与相应PMFwat的V1位置一致［图S12和图S13（A）（见本文支持信息）Merz力场的Li+的偏差最大， 但不超过0.04 nm］. 而另外3种离子（Na+、 K+和Cl-）的PMFads最小值出现在更靠近石墨烯的位置， 与相应PMFgra波谷位置一致［图S12和图S13（B）］. 这是因为， Na+， K+和Cl-等离子与水作用比较弱（如， 它们溶剂化自由能的绝对值比Li+， Mg2+和Ca2+的小［52～55］），所以当离子接近石墨烯时， 它们因水合层变形或脱水造成的PMFwat上升比较缓慢， 无法抵消PMFgra的下降趋势（考虑离子-π作用后， PMFgra及其变化均不可忽略下降）： 它们的总和（PMFads）也下降， 直到离子进一步接近石墨烯， PMFgra开始上升时为止. 所以Na+， K+和Cl-的PMFads的最小值位置由PMFgra的波谷位置决定（图S12）. 而Li+， Mg2+和Ca2+则与之相反， 当它们水合层变形或脱水时PMFwat上升迅速， 占主导地位； 故PMFads的最小值位置由PMFwat的V1决定（图S12）.

2.3 盐溶液/石墨烯界面上的离子吸附

由于实验或实际应用中与石墨烯接触的都是一定浓度的盐溶液. 进一步使用εLi-BC及εiio-nC-π参数模拟了浓度1 mol/L 的盐溶液/石墨烯界面体系［图1（B）］， 模拟的电解质分别为LiCl， NaCl， KCl， MgCl2和CaCl2］. 使用εLBi-C参数时， 各阴阳离子在界面附近的密度分布与体相非常接近（图7）， 表明离子在石墨烯表面的吸附很微弱. 这是因为εLBi-C参数低估了离子-石墨烯相互作用. 相反， 当使用εion-πi-C时， 各离子在石墨烯表面都呈现出明显的吸附峰（z＞0.5 nm时迅速衰减至接近体相密度， 图7）. 这表明强烈的离子-石墨烯相互作用将离子从溶液内部吸引到盐溶液/石墨烯界面上［36，37，78］； 所以能否准确描述该相互作用对准确模拟盐溶液/石墨烯界面体系至关重要. 进一步发现， 石墨烯表面各阴阳离子的吸附峰位置与相应PMFads最小值的位置十分接近（偏差不超过0.04 nm， 图S14， 见本文支持信息）. 但是， 各阳离子吸附峰高度与相应（单离子）Eads的大小顺序并不完全一致； 各盐溶液的Cl-吸附峰高度也不相同. 此外， 5种盐溶液-石墨烯界面上， LiCl的Cl-离子吸附峰明显低于另外4种盐的情况. 原因可能是， 一价离子Li+对Cl-的吸引力不如二价离子Ca2+和Mg2+， 且在界面上的浓度也低于其它阳离子， 对Cl-界面吸附的促进作用较弱. 这些结果表明， 在一定浓度的盐溶液-石墨烯界面体系中， 石墨烯、 水与离子之间的相互作用对离子浓度分布有重要影响； 而离子-离子之间的相互作用［51］也不可忽略.

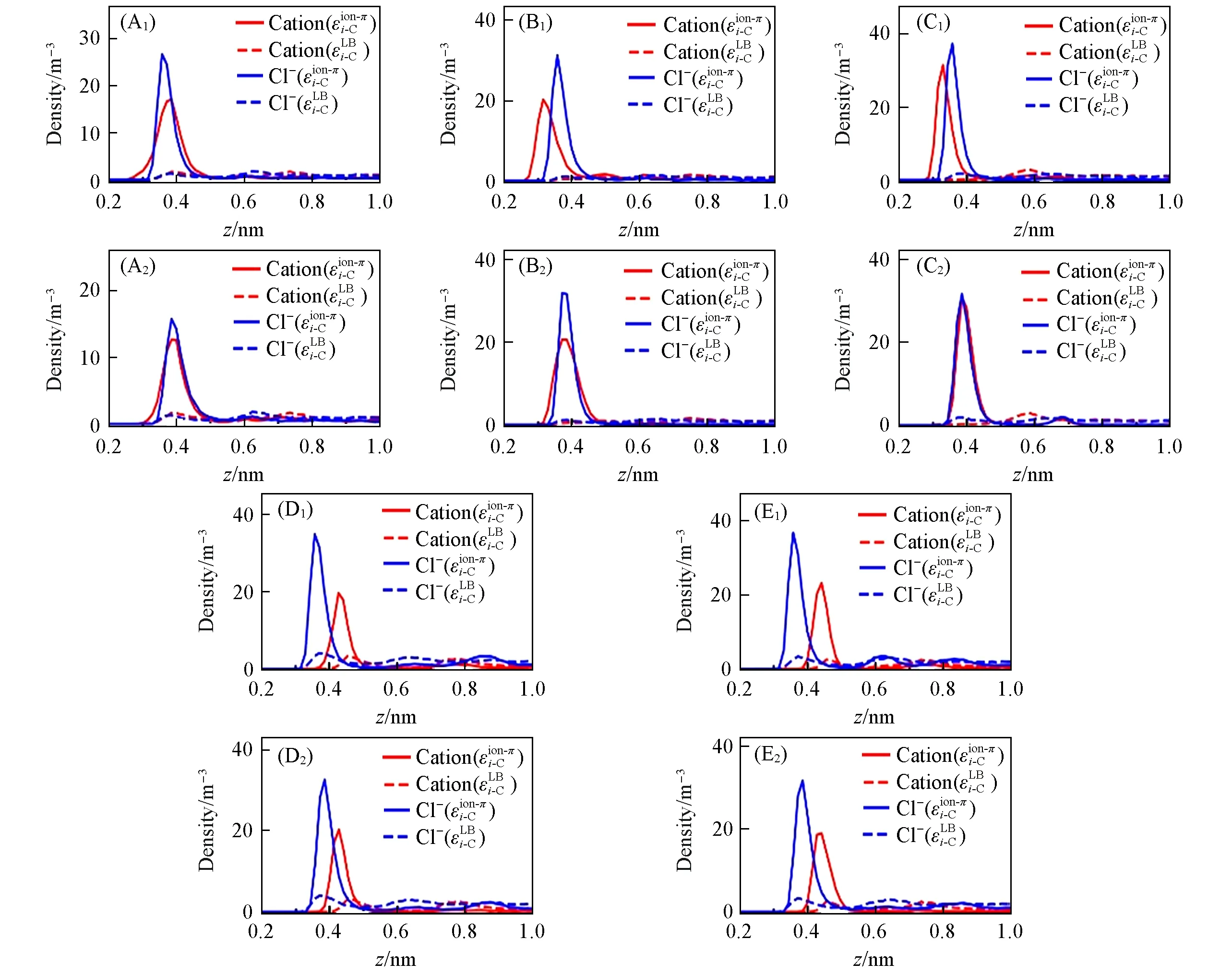
Fig.7 Ion’s density profile along 1 mol/L electrolyte solution/graphene interface

3 结 论

发展了溶液中Li+， Na+， K+， Mg2+， Ca2+和Cl-离子与石墨烯相互作用的LJi-C力场参数（优化后力场），其模拟得到的离子在（溶液中）石墨烯表面的吸附自由能（PMFads阱深）与量子化学计算结果一致， 表明它们可准确描述离子与石墨烯之间的离子-π相互作用. 作为对比， Merz和Netz这两套力场参数（优化前力场）无法描述离子-π作用， 模拟的离子吸附自由能很接近0， 甚至不吸附. 还将离子在石墨烯表面吸附的PMFads分解为离子-石墨烯（PMFgra）、 离子-水（PMFwat）相互作用的分别贡献. 发现无论用优化前还是优化后力场参数模拟， PMFgra均与离子-石墨烯相互作用势能曲线一致. 各阳离子PMFwat在z＜1.0 nm时都呈现出1个极大值和2个极小值（z＞1.0 nm时基本为0）， 而PMFwat极小值位置、 石墨烯表面两个高密度水层的位置、 （离子接近石墨烯时）水合层开始脱水的位置这三者有明显关联. 进一步研究了离子接近石墨烯时其周围水密度分布的变化. 这些结果都说明离子接近石墨烯时， 其PMFwat由离子水合层变形（或脱水）及其与石墨烯表面水层相互作用这二者共同调控. 还分别用优化前及优化后力场参数模拟了更接近实际问题的各种1 mol/L盐溶液/石墨烯界面， 发现优化后力场参数可准确描述界面离子吸附现象， 且各阴阳离子的吸附峰位置与对应的PMFads最小值位置基本一致. 作为比较， 优化前力场模拟的各阴阳离子在石墨烯表面的吸附非常微弱. 调节的是离子与石墨烯的作用参数， 而不是直接调节离子LJ参数， 所以离子与其它分子（如水）的作用及离子在水溶液中行为均不受影响. 开发的（溶液中）离子-石墨烯相互作用力场及对石墨烯表面离子吸附机制（尤其是其中的溶剂效应调控作用）的探讨可为石墨烯或其它二维材料的科学研究及相关纳米器件开发提供借鉴和指导.

支持信息见http: //www.cjcu.jlu.edu.cn/CN/10.7503/cjcu20230155.

感谢英国曼彻斯特大学Christopher D. Williams教授关于溶剂模型和吸附自由能方面的建议.