阿基米德对圆周率之估计及其与刘徽之“割圆术”的比较(续1)
欧阳顺湘
(哈尔滨工业大学(深圳)理学院 518055)
3 应用角平分线定理与勾股定理
阿基米德计算圆周率的主要思想已为众人所熟知:分别从圆内接、圆外切正六边形开始,通过角的平分,递推估计圆内接和圆外切的正12、24、48、96边形的边长,最终由圆内接和圆外切正96边形的周长的估计得到圆周率的下界和上界估计. 为更好地理解阿基米德是如何使用角平分线将正多边形的边数倍增的,我们具体解释如何从圆内接(外切)正六边形得到圆内接(外切)正十二边形.
图3展示了如何通过角的等分从圆O的内接正六边形ABCDEF得到内接正十二边形AA′BB′CC′DD′EE′FF′. 不失一般性,我们仅解释如何得到点C′.AC′是∠CAD的角平分线(等价地,OC′是∠COD的角平分线),C′在圆上. 由此可以由圆内接正六边形ABCDEF的边CD得到正十二边形AA′BB′CC′DD′EE′FF′的两条边CC′,C′D.
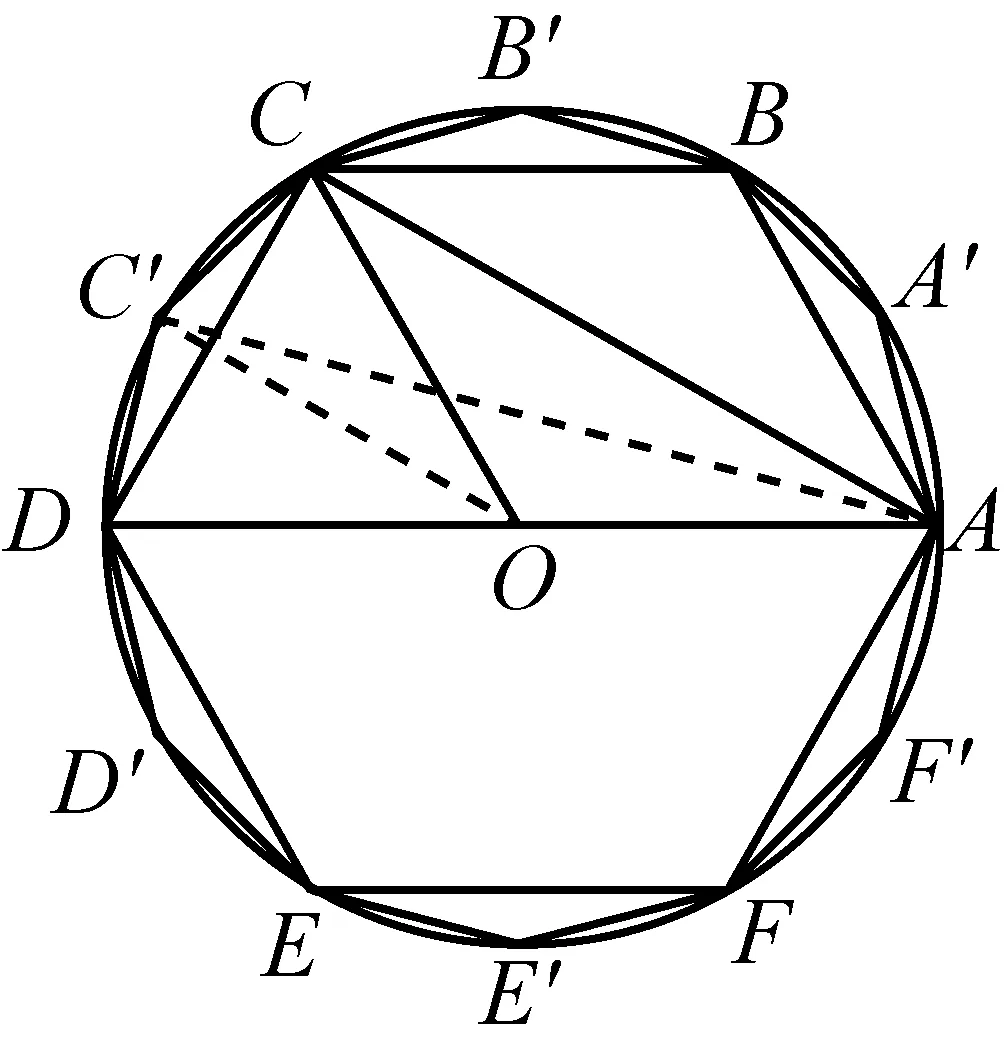
图3 通过平分角从内接正六边形得到内接正十二边形
图4展示了如何通过角的等分从圆O的外切正六边形ABCDEF得到圆外切正十二边形A′B′C′D′E′F′G′H′I′J′K′L′. 同样,不失一般性,我们仅解释如何得到点G′. 在图4中,OG′是∠QOD的角平分线,其中Q在圆上,是多边形ABCDEF的边DE与圆的切点,G′在DE上.

图4 通过平分角从外切正六边形得到外切正十二边形
引理2如图5,设AC外切圆O于A点,

图5 角平分线定理的应用(外切情形)
OD平分∠AOC,D在AC上,则
(3.1)


设θ=∠COA,用三角函数表示上面的结论(3.1),有
(3.2)
引理3如图6,设AB为直径,C为半圆上的一点,AD平分∠CAB,且交圆于D,则

图6 角平分线定理的应用(内接情形)
(3.3)
证明设AD交BC于d.注意到AD是角平分线,可知∠DAB=∠CAd,再注意到∠ADB=∠ACd是直角,可知△ADB与△ACd相似. 于是有
(3.4)
(3.5)
综合(3.4)与(3.5)可得(3.3).
设∠CAB=θ,则(3.3)相当于
(3.6)
形式上,(3.6)与(3.2)相同. 由此可见,引理2,引理3得到的结论类似,都是利用原有直角三角形的边的比例来计算由角平分线得到的新的直角三角形中直角边的比例. 这两个结论是比较突出的,如在[2,13]中也都单独提出.
在上面的两个引理中,出现了两直角边之比以及斜边与直角边之比. 在一个直角三角形中,如果已知直角边之比,则由勾股定理,斜边与直角边之比也就确定了. 阿基米德在圆周率的计算中反复应用了这一做法. 为方便引用,我们将这个结论写成如下引理.
引理4设AB为直角三角形△ABC的斜边(∠BAC为直角),则
(3.7)
设∠ABC=θ,则(3.7)可表示为
(3.8)
在三角形式的勾股定理1=sin2θ+cos2θ的两边同时除以sin2θ≠0,再开方可立即得到等式(3.8).
4 圆周率的上界
如图7,设O为圆心,AC为外切正六边形的半条边,A为切点,OA为半径. 显然,OA与AC垂直. 设AC上的点D,E,F,G使得OD,OE,OF,OG分别平分∠COA,∠DOA,∠EOA,∠FOA,则AD,AE,AF,AG分别为圆O的外切正12、24、48、96边形的半条边. 阿基米德通过递推依次计算AO与AC,AD,AE,AF,AG之比的下界来得到圆周率的上界.
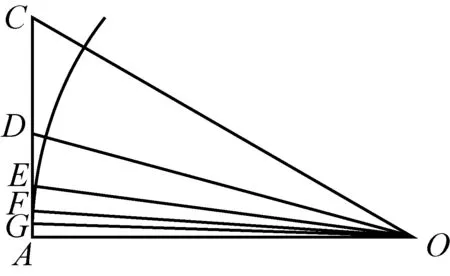
图7 圆外切正6,12,24,48,96边形的半条边
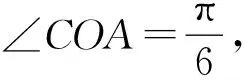

(4.1)
外切正24边形根据引理4,并利用(4.1),可得
(4.2)
因为OE是∠DOA的角平分线,应用引理2,并利用(4.2),可得
(4.3)
外切正48边形根据引理4,并利用(4.3)可得
(4.4)
因为OF是∠EOA的角平分线,再次应用引理2,并利用(4.4)可得
(4.5)
外切正96边形根据引理4,并利用(4.5)可得
(4.6)
因为OG是∠FOA的角平分线,再次应用引理2,并利用(4.6)可得
圆外切正96边形的周长大于圆周长,所以
96×2×AG>2π×OA.
由此可得π的一个上界估计①
① 利用圆外切正6,12,24,48边形也可以分别估计得到圆周率的上界:
它们的具体数值可参考后文表1.:

表1 阿基米德求圆周率上界的迭代,各步所得圆周率的估计及其理论值(1) 近似值未作四舍五入,表2同理.
(4.7)
5 圆周率的下界
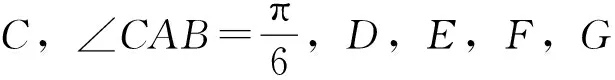

图8 圆内接正6,12,24,48,96多边形的一条边


(5.1)
于是,由引理4以及(5.1),可得
(5.2)
内接正24边形因为EA平分角∠DAB,应用引理3以及(5.2),可得
(5.3)
因此,根据引理4以及(5.3),可得
(5.4)
内接正48边形因AF平分∠EAB,应用引理3以及(5.4),可得
(5.5)
因此,由引理4以及(5.5),可得
(5.6)
内接正96边形因AG平分∠FAB,应用引理3以及(5.6),可得
(5.7)
因此,由引理4以及(5.7),可得
(5.8)
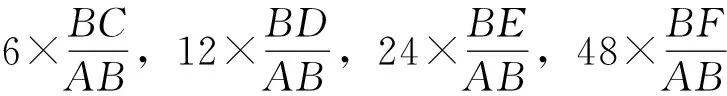
6 阿基米德的迭代
本节我们考察阿基米德的迭代的一般化,展示如何用三角函数表示这个迭代过程. 我们还将阿基米德的迭代联系到了其他迭代公式.
6.1 外切与圆周率的上界
如图9所示,设圆O的半径为r,m≥3,n≥0,AC为圆外切正m2n边形的半条边,A为切点,则∠COA=θn,其中
如图9所示,对任意n≥0,记
注意到an是圆半径与其外切正m2n边形半条边之比. 所以,
为圆外切正m2n边形的边长. 我们将在本小节的最后讨论bn的几何意义. 对给定的半径r,根据相似三角形知识,an,bn仅依赖于边数,或说仅依赖于θn的大小. 因为
由引理2以及引理4,可得
(6.1)
利用三角函数,可知
(6.2)
因此(6.1)即(亦可参考(3.2),(3.8))
(6.3)
同时,初值也可以用三角函数表示为

圆外切正多边形的周长大于圆周长,即Pn>2πr.由此可得圆周率的上界
以上过程是阿基米德的计算程序. 如果利用三角函数恒等式,自然可以直接得到迭代公式(6.3),也就是说,三角函数sinθn,tanθn的值可以通过迭代计算. 进而可以得到半径为r的圆外切正m2n边形的边长2rtanθn,从而可得圆周率的上界m2ntanθn.
我们现在分析bn的含义. 注意到△OAC∽△OEB,可得
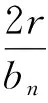
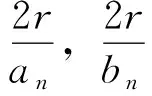
6.2 内接与圆周率的下界
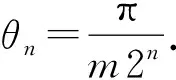

图10 阿基米德的迭代(内接情形)
如图10所示,对任意n≥0,记


由引理3以及引理4,可得
(6.4)
上述递推公式与外切情形的递推公式(6.1)类似(后文将说明它们实际上是同一个递推公式).
因为圆内接正多边形的周长小于圆周长,所以pn<πd.由此可得圆周率的下界
注意到△ABC∽△OED,可得
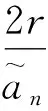
(6.5)
6.3 估计与迭代

(6.6)
则综合前面的计算可得
πn<π<Πn.
(6.7)
从三角函数的角度,(6.7)可以从如下不等式(参图11)直接得到
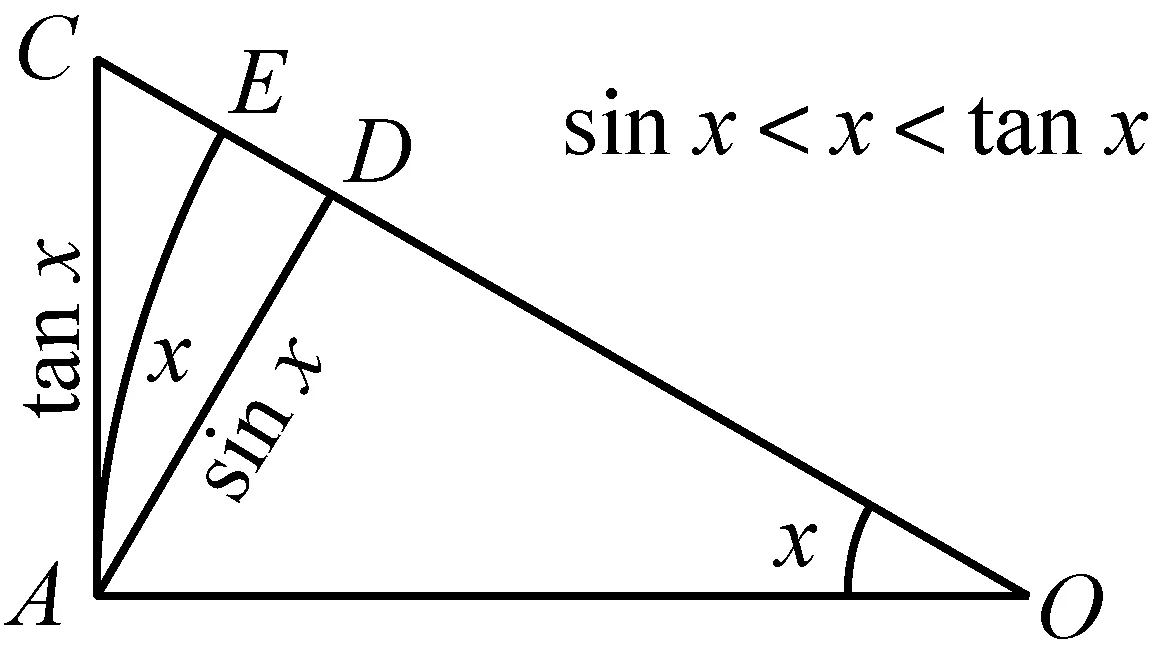
图11 弧的上下界(设OA=1,则
(6.8)
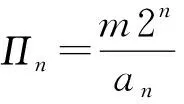

我们可以比较阿基米德通过圆外切(相应地,内接)正6、12、24、48、96边形(即m=6)得到的圆周率上界(相应地,下界)估计与通过计算机计算正切tanθn(相应地,正弦sinθn)(n=0,1,2,3,4)所得圆周率上界(相应地,下界)估计.
6.4 阿基米德的迭代的变形
根据(6.1),有
因此
(6.9)
所以,阿基米德的迭代(6.1)也可以改写为如下形式:
(6.10)
利用在(6.6)中定义的πn,Πn:
可得
因而可将(6.9)表示为
所以
(6.11)
即πn+1是πn,Πn+1的几何平均.
又由(6.10)的第一式可得
即有
(6.12)
这表明Πn+1是πn与Πn的调和平均.
至此,我们将阿基米德计算圆周率的原始迭代公式(6.1)重新表述为(6.10),进而利用πn,Πn+1将其表述为如下迭代公式
(6.13)
其初值为

记
则由(6.13)可得如下算术平均-几何平均关系:
(6.14)
其初值为
如此迭代来估计圆周率可以减少一些运算. 用算术平均-几何平均迭代来计算圆周率是值得关注的,如高斯在研究椭圆积分时曾得到圆周率与算术平均-几何平均迭代的关系.
利用三角函数表示
πn=m2nsinθn,Πn=m2ntanθn,
不难对πn,Πn以及cn,dn的意义给出一些解释(在介绍阿基米德的计算时,实际已经解释过πn,Πn的意义),由此可从不同角度理解迭代公式(6.13)和(6.14).
如图12,设圆O的半径为r,AD,AC分别为圆内接、外切正m2n边形的半条边,则

图12 圆与其内接正多边形和圆外切正多边形(或正多边形与其内切圆和外接圆)
OD=rcosθn.
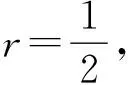
=m2nsinθn=πn,
外切正m2n边形的周长为
=m2ntanθn=Πn.
也就是说,πn,Πn为直径为1的圆内接、外切正m2n边形的周长. 此时,(6.13)相当于19世纪法国数学家利奥内(Lionnet)、西罗德(P.-L. Cirodde)和于埃(Huet)各自得到的递推公式(参[12,定理3]).
(2)设r=1,n>0,则△OAD的面积为
因此圆内接正m2n边形的面积为
=m2n-1sinθn-1=πn-1.
设n≥0,△OAC的面积为
因此圆外切正m2n边形的面积为
=m2ntanθn=Πn.
也就是说,设n≥0,则πn,Πn可分别看作单位圆内接正m2n+1边形、外切正m2n边形的面积. 此时,(6.13)相当于法国数学家邵林(J. Saurin)于1737年在法国科学院院刊上发表的面积递推公式(参[12,定理2]).



由此可见,三个分别于19、18、17世纪发现的递推公式本质上都可归于阿基米德的迭代公式. 读者可参考[12]及其中的相关文献以获取17~19世纪法国数学家计算圆周率的相关递推公式的更多信息.
(未完待续)

