Thermodynamic re-assessment of the Mg–Gd–Y ternary system coupling with the driving forces for phase precipitations during aging process
Xiaopan Wu,Changrong Li,Cuiping Guo,Zhenmin Du
School of Materials Science and Engineering,University of Science and Technology Beijing,Beijing 100083,China
Abstract Based on the available experimental phase equilibrium relations and aging precipitation sequences,the Mg–Gd–Y ternary system has been thermodynamically re-assessed by means of CALPHAD technique.To simulate the experimentally reported aging precipitation sequence,α(Mg)SS(supersaturated)→GP zones (D019-type,metastable)→β’-Mg7Gd (c-bco,metastable)→β1-Mg3Gd (fcc,metastable)→β-Mg5Gd(fcc,stable) near the Mg–Gd side,and α(Mg)SS(supersaturated)→β’-Mg7Y (c-bco,metastable)→β-Mg24Y5 (bcc,stable) near the Mg–Y side,the effective nucleation driving forces obtained by deducting the nucleation resistances from the thermodynamic driving forces are calculated and analyzed.Two metastable components,GP zones (D019-type) and β’ (c-bco) ordered from α(Mg)SS,do not exist in the stable equilibrium phase diagram but appear in the annealing process of typical alloys.The Redlich–Kister equations are adopted to describe three solution phases,Liquid,HCP_A3 and BCC_A2.The intermediate compounds Mg2Y,Mg24Y5,Mg2Gd,Mg3Gd and Mg5Gd are expressed by the formulas of (Mg,Y)2/3(Gd,Mg,Y)1/3,Mg24/29(Gd,Mg,Y)4/29Y1/29,(Gd,Mg)2/3(Gd,Mg,Y)1/3,(Gd,Mg)3/4(Gd,Mg,Y)1/4 and Mg5/6(Gd,Mg,Y)1/6,respectively.In particular,the two-sublattice models (Gd,Mg,Y)1/2(Gd,Mg,Y)1/2,(Gd,Mg,Y)3/4(Gd,Mg,Y)1/4 and (Gd,Mg,Y)7/8(Gd,Mg,Y)1/8 have been respectively used to describe the stable Mg(Gd,Y) (BCC_B2) alloy compound as well as the metastable GP zones (D019-type) and β’ (c-bco) phase,in order to cope with the order-disorder transitions.A set of self-consistent thermodynamic parameters has been obtained to ensure the thermodynamic calculations well consistent with the reported experimental data,containing not only the stable equilibrium phase diagram but also the aging precipitation sequence.
Keywords: Mg–Gd–Y ternary system;Thermodynamic re-assessment;Aging precipitation sequence;Nucleation driving force;CALPHAD technique.
1.Introduction
Light weight Mg alloys,featured by the high specific strength,low density,easy recycling and excellent castability,have received great attention owing to many potential applications in the areas of aerospace,automotive and 3C industries [1–4].However,the unfavorable behaviors at elevated temperature seriously hinder the wide applications of Mg alloys.It has been found that the addition of rare earth(RE) elements can significantly improve the mechanical properties at room and high temperatures by solid solution and aging precipitation strengthening effects [5–11].Efforts have been made to research and develop different types of high property Mg–RE alloys,among which the Mg–Gd–Y alloy has become one of the promising candidate due to its higher strength,superior creep resistance and preferable heat resistance compared with the conventional Mg alloys such as the WE54 alloy [3,6,12,13].In addition,the heavy RE elements Gd and Y not only have the large equilibrium solid solubilities inα(Mg) (HCP_A3) matrix,namely,4.53 at.% at 821 K for Gd and 3.75 at.% at 839 K for Y,but also have the large solid solubility reductions exponentially with the decrease of temperature,namely,0.61 at.% and 0.75 at.% at 473 K for Gd and Y respectively [1].Therefore,the Mg–Gd–Y alloy is of the advantages of the age hardening process.
Recently,the research on Mg–Gd–Y alloys has focused on the microstructural evolution,mechanical property,precipitation sequence,orientation relationship between the precipitated phases and theα(Mg) matrix,etc.In general,the aging precipitation sequences of Mg–Gd–Y ternary alloys are supposed as the following ones [1,2,13–20]:
In the above aging precipitation sequences,the crystalline structures of phases,orientation relationships,habit planes and morphologies are similar to those of the Mg–Gd and the Mg–Y binary alloys [21,22].
The metastable GP zones (D019-type) are a few independent hexagonal networks including RE-rich atoms appeared in the early stage of aging precipitation.Theβ’ zones (Mg7Gd and Mg7Y) are the coherent precipitates including zigzag arrangements of Mg and RE elements.Both the GP and theβ’ zones are the ordered structures of the disordered phase HCP_A3 [23],and are all coherent interface with theα(Mg)matrix [7,11,13,24–28].Bothβ1andβphases are all incoherent with theα(Mg) matrix [7,28,29].As for the metastableβ’ precipitates and GP zones (D019-type),the strengthening effect of the former is superior to that of the latter[1,2,11,30].
In the light of the relationship of the equilibrium phase diagram and the stability of precipitated phases,although theβ’phase and GP zones are metastable,both need to be considered in the assessment of the Mg–Gd–Y ternary system since there exist the thermodynamic driving forces for them to precipitate preferentially during the aging process.Therefore,it is necessary to re-optimize the Mg–Gd–Y ternary system after the successful optimizations of the Mg–Gd and the Mg–Y binary systems coupled with the aging precipitation sequences[21,22].
Theoretically,there must be a positive driving force to make the second phase precipitate from the supersaturated solid solution.When a very small amount of new precipitate is formed in the beginning of precipitation transformation,the change of the total free energy of the system includes the decrease of the chemical free energy (the thermodynamic nucleation driving force) and the increase of the phase boundary energy and elastic strain energy (the nucleation resistances).In the present work,the effective nucleation driving force is adopted,which is defined as the difference between the thermodynamic nucleation driving force calculated by the thermodynamic parameters and the nucleation resistances[21,22],meaning the usable nucleation driving force after overcoming the nucleation resistances.
The relative values of the effective nucleation driving forces are used to simulate and predict the aging precipitation sequence of the Mg–Gd–Y ternary alloys.The larger the calculated effective nucleation driving force is,the earlier the phase precipitates.
The nucleation resistances are considered differently for the precipitated phases with different interface structures in the present work.The metastable precipitated phases with coherent interfaces are easier to precipitate from theα(Mg) matrix in a homogeneous nucleation way,and their elastic strain energies are greater than the phase boundary energies,constituting the major factor of the nucleation resistance.Therefore,the elastic strain energies of the GP zones (D019-type)/α(Mg)andβ’-Mg7M/α(Mg) in the Mg–Gd–Y ternary system are mainly considered.On the contrary,the metastable and the stable precipitated phases with incoherent interfaces are prone to precipitate from the existingα(Mg) grain boundary in a heterogeneous nucleation way,and their phase boundary energies between the precipitated phases and theα(Mg) matrix are greater than the elastic strain energies and are considered as the main resistance to the growth of the nucleated particles.Thus,the increase of the phase boundary area/energy and the decreased of the grain boundary area/energy are the main factors to be considered for the Mg3Gd,Mg5Gd,Mg24Y5,Mg2Gd and Mg2Y phases.
The thermodynamic re-optimization coupled with the driving forces for phase precipitations during aging process is of special significance.Firstly,in order to make a reasonable explanation for the aging precipitation sequence of the Mg–Gd–Y ternary alloy,the effective nucleation driving forces of the precipitated phases must be positive.Secondly,in order to improve the mechanical properties of the Mg–Gd–Y ternary alloy,the strengthening effects of the meta-stably precipitated phases must be fully developed and used.Thermodynamic calculations can provide the theoretical basis and useful guidance for the design and development of age hardening Mg–Gd–Y ternary alloys.
The equilibrium phase diagrams and the thermodynamic driving forces are calculated by means of the CALPHAD(CALculation of PHAse Diagrams) technique,while the elastic strain energy,the phase boundary and the grain boundary energies,which constitute the nucleation resistances,are calculated through self-programming.
2.Literature review
2.1.Mg–Gd–Y ternary phase diagram information
Three isoplethal sections of the Mg–Gd–Y ternary system with the ratios of weight fractionw(Gd)/w(Y)=3,1 and 1/3 were first investigated experimentally by Drits et al.[31].The intermediate compounds Mg24Y5and Mg6Gd were treated as same the stoichiometric compoundβ-Mg6(Gd,Y)in their study.Later,an isothermal section of the Mg–Gd–Y ternary system at 773 K was determined by Giovannini et al.[32]using the optical microscope (OM),scanning electron microscope (SEM),X-ray power diffraction (XRD) and electron probe microanalysis (EPMA).No formation of any new ternary phase was observed.A continuous solid solubility of the phase Mg(Gd,Y) with BCC_B2 structure ordered from BCC_A2 existed from the Mg–Gd side to the Mg–Y side.In addition,the solubilities of the third component in the binary phases of the terminal binary systems were also reported.All the experimental studies have been critically reviewed and evaluated by Schmid-Fetzer et al.[33],and at the same time,the invariant reactions atT <833.15 K involving the phases of Mg24Y5,Mg5Gd,HCP_A3 and Liquid have been proposed,according to the interpretation of the measured results by Drits et al.[31].
Based on the available experimental data,the Mg–Gd–Y ternary system was optimized by Guo et al.[34],and a set of self-consistent thermodynamic parameters was obtained.The thermodynamic calculation and experimental study of the Mgrich region in the Mg–Gd–Y ternary system were carried out by another Guo et al.[35]using the CALPHAD approach and the differential scanning calorimetry (DSC) analysis,respectively.They found that the as-cast solidification sequences of the phases Mg24Y5and Mg5Gd were related to the contents of Gd and Y.In the Mg-1Gd-7Y (wt.%) alloy,Mg24Y5solidified from the supersaturatedα(Mg) solid solution prior to Mg5Gd.However,the solidification sequence was the opposite in the Mg-5Gd-2Y (wt.%) alloy.During their optimizations in Refs.[34,35],the phase Mg5Gd was regarded as the linear stoichiometric compound Mg5(Gd,Y),while the phase Mg24Y5was treated differently as the intermediate alloy compound Mg24(Gd,Mg,Y)4Y in Ref.[34]and the linear stoichiometric compound Mg24(Gd,Y)5in Ref.[35].
Later,the Mg–Gd–Y ternary system was re-assessed by Gröbner and Schmid-Fetzer [36]during their optimization of the Mg–Ce–Gd–Y quaternary system.In Ref.[36],the thermodynamic data for pure components in literature was used,and the different models for the intermediate compounds Mg(Gd,Y),Mg2Y and Mg24Y5with Mg(Gd%,Y%),Mg2(Gd,Y%) and Mg24(Y%,Gd,Mg)5,respectively,were adopted.The symbol“%”indicates the majority of constituent elements of a compound.Recently,Szakács et al.[37]investigated the microstructural evolutions of as-cast alloys MgxY-yGd (x+y=15 wt.%) and compared with the thermodynamic calculations.The calculations suggested that Mg24Y5solidified prior to Mg5Gd,and the Mg24Y5was observed experimentally.
The phase diagram information of the Mg–Gd–Y system reported in literatures is in the stable phase equilibrium state.Recently,the successful optimizations of the Mg–Gd and the Mg–Y binary systems coupled with the aging precipitation sequences[21,22]not only reproduced the experimental equilibrium phase relations and thermochemical properties well,but also effectively predicted the aging precipitation sequences.On this occasion,it is necessary to perform the thermodynamic re-optimization of the Mg–Gd–Y ternary system coupling with the driving forces for phase precipitations during aging process.
2.2.Precipitation sequence in the Mg–Gd–Y ternary system
The aging precipitation behavior of the Mg–Gd–Y ternary alloys has been studied by many experiments.The early stage of aging treatment of the alloy Mg-2.1Gd-0.6Y (at.%) aged at 473 K was investigated by Nakagawa et al.[14,15]using high resolution transmission electron microscopy (HRTEM)and selected area electron diffractions (SAED).The result in Ref.[14]indicated thatβ’’ (D019-type GP zones) and pre-β’structure (single zigzag line on {100}α) were mainly observed at the early stage of aging for 2 h,leading to the slow increase of hardness;β’’,β’ (zigzag lines,containing at least three parallel pre-β’ structures) and the precipitations with a width of 1.1 nm featured by the (020)β′lattice plane were observed simultaneously at aging time for 4 h,leading to the rapid increase of hardness;and the phasesβ’’ andβ’ co-existed at aging time for 64 h withβ’ as the predominant phase,leading to the maximum value of hardness,corresponding to the peak aging stage.Meanwhile,the result in Ref.[15]showed thatβ’’(D019,a=0.642 nm,c=0.521 nm)was confirmed prior to theβ’(c-bco,a=0.642 nm,b=2.223 nm,c=0.521 nm) for 2 h.β’ was observed obviously for 8–64 h,and the amount of the precipitated phaseβ’was prevail over that ofβ’’ for 64 h.The phasesβ’’ andβ’were further identified by Kawabata et al.[16]and Matsuoka et al.[17].
The microstructural evolutions of the alloy Mg-2.9Gd-0.8Y(at.%) aged at 473 K for 2–64 h were first investigated by Nakagawa et al.[15]and Kawabata et al.[16]using HRTEM and SAED in the same year.In the aged alloy Mg-2.9Gd-0.8Y (at.%),the precipitated phase observed wasβ’ for 2–64 h[15,16].However,it was uncertain whether the phaseβ’’precipitated within the aging time 2 h.Afterwards,the early aging stage of the alloy Mg-2.9Gd-0.8Y (at.%) aged at 473 K was investigated in detail by Matsuoka et al.[18,19]using HRTEM,high angle annular dark field-scanning transmission electron microscopy(HAADF-STEM)and image simulations.The results indicated that bothβ’’ andβ’ were observed within the aging time 2 h.In addition,the precipitated phases,pre-β’’ structure,pre-β’ structure,β’’ andβ’ were confirmed by HRTEM and HAADF-STEM at the under aging stage.The pre-β’’ structure was also defined as incomplete hexagons with a short-range ordered structure close to D019,and was considered to be the first solute atom segregation regions[23].β’’ consists of at least three adjacent pre-β’’ structures.The amount of the pre-β’’ structure precipitated during quenching as well as during the early stage of aging treatment was obviously more than that of theβ’ structure.After long enough aging time,the pre-β’’ structure transformed intoβ’’ or preβ’ structure or evenβ’ phase.
It is reported that the age hardening curves of these two alloys mentioned above are almost parallel to each other,and the hardness of the former alloy is lower than that of the latter alloy [15,16].
The microstructural evolutions of the alloy Mg-0.992Gd-0.585Y (at.%) during the solid solution and the aging treatments were investigated by Yang et al.[13]using HRTEM,OM,SEM,EDS and XRD.The results showed that the age hardening behavior was most significant at the aging temperature 448 K rather than 473 and 498 K.The microstructures of this alloy aged at 448 K for different aging times were observed in detail.Theβ’’ firstly precipitated from theα(Mg)matrix during the under aging stage of 4–32 h,leading to the slow increase of hardness.In the aging stage of 32–100 h,theβ’ began to precipitate,and the phasesβ’’ andβ’ co-existed,causing the rapid increase of hardness.The hardness reaches the maximum at 100 h.In the over aging stage of more than 100 h,theβ’ gradually coarsened and the metastableβ1and stableβprecipitated,resulting in the decrease of hardness.
Recently,the precipitation sequence of the Mg–Gd(–Y) alloys predicted by Wang et al.[20]using the first principle method was the same as that proposed by Yang et al.[13].
In present work,the precipitates pre-β’’ andβ’’ as well as pre-β’andβ’in the previous studies are referred to as the GP zones (D019-type) andβ’,respectively,for the convenience of describing the transformation process in the early stage of aging treatment.The commonly recognized aging precipitation sequence of the Mg–Gd–Y ternary system near the Mg–Gd side is summarized as follows [1,2,13–20]:
3.Thermodynamic modeling
3.1.Pure elements
The Gibbs free energy function for the pure elementi(i=Gd,Mg,Y)in the phaseφis described by the following form:
The molar Gibbs free energy functions of Gd,Mg and Y are taken from the SGTE (Science Group Thermo data Europe) compiled by Dinsdale [38].
3.2.Solution phases
In the Mg–Gd–Y ternary system,the solution phaseφ(φ=BCC_A2,HCP_A3 and Liquid) is regarded as the substitutional solution model.The molar Gibbs free energy of the phaseφcan be described as the following:
3.3.Intermetallic compounds
3.3.1.The Mg2Gd,Mg3Gd and Mg5Gd phases
According to the previous work[21,40],the phases Mg2Gd(Laves_C15 with the prototype of Cu2Mg) and Mg3Gd(FCC_D03with the prototype of BiF3) in the Mg–Gd binary system were described by the formulas (Gd,Mg)2/3(Gd,Mg)1/3and (Gd,Mg)3/4(Gd,Mg)1/4,respectively.In the present optimization,considering the solubility of Y,these phases are described by the formulas (Gd,Mg)2/3(Gd,Mg,Y)1/3and (Gd,Mg)3/4(Gd,Mg,Y)1/4,accordingly.The two-sublattice model (Gd,Mg)p(Gd,Mg,Y)q,withp+q=1,is used to describe the phaseθ(θ=Mg2Gd and Mg3Gd),and the corresponding expression of the Gibbs free energy per mole atoms of the phaseθis given as the following:
The intermetallic compound Mg5Gd (FCC with the prototype of GdMg5) in the Mg–Gd binary system has a homogeneity range and is expressed by the two-sublattice formula Mg5/6(Gd,Mg)1/6[21,40].It is treated with the model Mg5/6(Gd,Mg,Y)1/6in the Mg–Gd–Y ternary system.Some Gd and Mg atoms are substituted by Y atoms in the second sublattice.The expression of the Gibbs free energy per mole atoms of Mg5Gd is as the following:
whereaandbare the parameters to be assessed.
3.3.2.The Mg2Y and Mg24Y5 phases
The intermetallic compounds Mg2Y (Laves_C14 with the prototype of MgZn2) and Mg24Y5(BCC_A12 with the prototype ofα-Mn) are respectively expressed by the formulas (Mg,Y)2/3(Mg,Y)1/3and Mg24/29(Mg,Y)4/29Y1/29in the Mg–Y binary system [22].Accordingly,the formulas(Mg,Y)2/3(Gd,Mg,Y)1/3and Mg24/29(Gd,Mg,Y)4/29Y1/29are used to describe these two phases in the Mg–Gd–Y ternary system.
The Gibbs free energy per mole atoms of Mg2Y is expressed as the following:
The Gibbs free energy per mole atoms of Mg24Y5is expressed as follows:
Thereinto,the meaning of each variable in Eqs.(9),(10) is similar to that in Eqs.(6)–(8).
3.4.Ordered phases
There are two metastable ordered phases,GP zones (D019-type) and Mg7M,transformed from the disordered phase HCP_A3,and one stable ordered phase MgM transformed from the disordered phase BCC_A2.It should be noted that the metastable phaseβ’-Mg7M in the Mg–Gd–Y ternary system is regarded as the Mg7Gd near the Mg-Gd side and the Mg7Y near the Mg-Y side,respectively.β’-Mg7M is used in the Mg-Gd-Y ternary system indicating the mixture of the Mg7Gd and Mg7Y.
The two-sublattice models (Gd,Mg)m(Gd,Mg)nand(Mg,Y)m(Mg,Y)nwithm=0.75 andn=0.25 for D019-type GP zones,m=0.875 andn=0.125 for Mg7Gd and Mg7Y,andm=n=0.5 for MgGd and MgY were respectively used to describe the order-disorder transitions in the Mg–Gd and the Mg–Y binary systems [21,22].Accordingly,the two-sublattice model (Gd,Mg,Y)m(Gd,Mg,Y)nis adopted in the present optimization.The Gibbs free energy per mole atoms of the ordered phase takes the following form:
4.Optimization and calculation
According to the reported experimental phase equilibrium relations in Refs.[31,32]and the aging precipitation sequence in Refs.[1,2,13–20],the present re-assessment work is carried out by means of Pandat software package [43].In addition,the DSC and the calculated phase transformation temperatures from another Guo et al.[35]are also adopted to compare with the present optimized results.The thermodynamic parameters of the Mg–Gd,the Mg–Y and the Gd–Y binary systems are taken from Refs.[21,22,34],respectively.The constituent binary phase diagrams are presented in Fig.1.
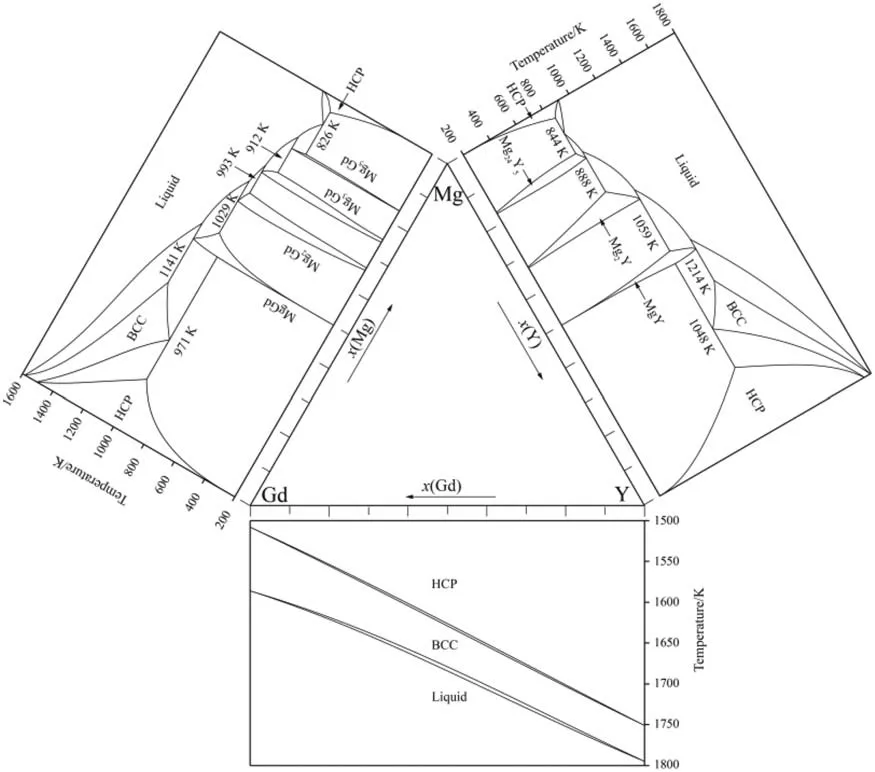
Fig.1.Binary phase diagrams [21,22,34]constituting the Mg-Gd-Y ternary system.
The models for the phases of the Mg–Gd–Y ternary system are listed in Table 1.In particular,both GP zones (D019-type) and Mg7M are treated as the ordered transition forms from the disordered HCP_A3 phase.For metastable ordered phases GP zones (D019-type) and Mg7M,they do not exist in the stable equilibrium phase diagram,but appear in the aging precipitation sequence.The thermodynamic parameters of the GP zones (D019-type) and Mg7M are obtained by the following methods:
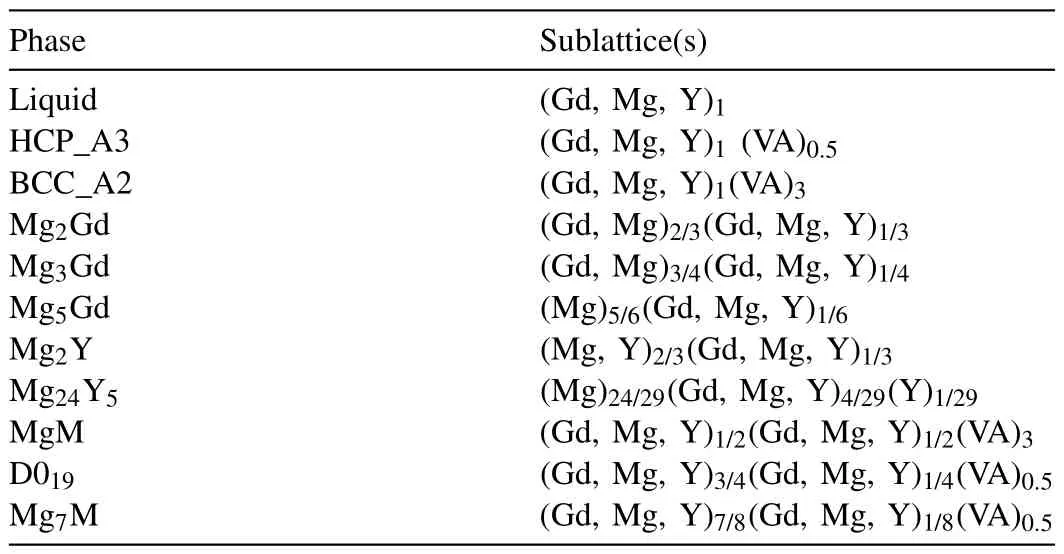
Table 1The constructed models for the phases of the Mg-Gd-Y ternary system.
Firstly,the thermodynamic parameters of all the stable phases including the disordered solution phase HCP_A3 are optimized based on the experimental phase equilibria.The optimizations for the metastable ordered phases GP zones(D019-type) and Mg7M are followed,by consideration of the ordering energies from the Gibbs free energy of the fundamental stable disordered HCP_A3 phase.During the thermodynamic optimization process of the metastable phases,GP zones (D019-type) and Mg7M can not destroy the original stable phase equilibrium relations,but the relative values of the effective nucleation driving forces must be able to predict the aging precipitation sequence of the Mg–Gd–Y ternary alloys appropriately and reasonably,as reported in literatures.The final optimized parameters are given in Appendix A.
It is worth mentioning that there are some important challenges in extending the calculation of nucleation driving force from binary system to ternary or even multi-component system.The thermodynamic calculations should well reproduce the experimental stable phase relations,such as isothermal sections,isopleth sections,liquidus surface projection and invariant reactions.Moreover,the calculated effective nucleation driving forces from large to small for the precipitated phases should be in agreement with the experimentally observed aging precipitation sequence,especially the transitive change from one sub-binary to another.Meanwhile,in order to convert the unit of phase boundary energy and grain boundary energy (J/m2) to the same unit of the thermodynamic nucleation driving force (J/mol),the size of precipitated phase is a very important link between J/m2and J/mol.
Fig.2 shows the steps of thermodynamic re-assessment in the present work.

Fig.2.The steps of thermodynamic re-assessment in the present work.
5.Results and discussions
5.1.Stable phase relations
The thermodynamic Gibbs energy expressions of the Mg–Gd–Y ternary system are assessed using Pandat software package in the present work,based on the available thermodynamic parameters of the three constituent sub-binary systems [21,22,34]as well as the ternary system [34].The corresponding stable and metastable phase diagrams are calculated by using the presently optimized parameters listed in Appendix A.The comparisons between the present calculated results and the experimental data as well as other thermodynamic optimizations are discussed accordingly.
Fig.3 presents the calculated isothermal section of the Mg–Gd–Y ternary system at 773 K,showing the comparisons of the present calculated results with the experimental data reported by Giovannini et al.[32],Fig.3(a),and with the previous thermodynamic assessment results [34,36],Fig.3(b).Compared with Refs.[34,36],the present calculated results can reproduce the experimental measurements better,especially in the two-phase regions of HCP_A3+Mg5Gd,HCP_A3+Mg24Y5,Mg2Y+Mg24Y5,Mg2Gd+MgM and Mg2Y+MgM and the three-phase regions of HCP_A3+Mg5Gd+Mg24Y5,Mg2Y+Mg5Gd+Mg24Y5,Mg2Y+Mg2Gd+Mg3Gd and Mg2Y+Mg2Gd+MgM.
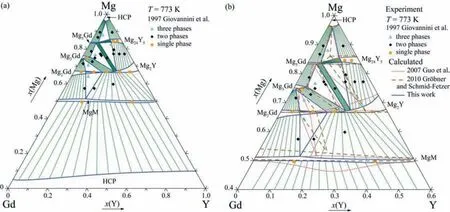
Fig.3.Calculated isothermal section of the Mg-Gd-Y ternary system at 773 K compared with the available experimental data [32]and the assessment results [34,36]: (a) Whole composition range;(b) Enlarged part of Fig.3(a),in which the assessment results [34,36]are superimposed.
Fig.4 displays the calculated liquidus surface projection.Table 2 gives the calculated invariant reactions involving the liquid phase and corresponding to Fig.4.Table 3 indicates the comparison between the experimental maximum solid solubilities in wt.% of the third component in binary phases of Ref.[32],the available thermodynamic calculations from Refs.[34,36]and the presently calculated results.Some differences between the calculated results and the experimental data are acceptable within the experimental uncertainties.

Table 2The calculated invariant reactions of the Mg-Gd-Y ternary system.

Table 3The maximum solid solubilities in wt.% of the third component in binary phases of the Mg-Gd-Y ternary system at 773 K.

Fig.6.Calculated isopleth section of the Mg-Gd-Y ternary system at w(Y)/w(Gd)=1 compared with the available experimental data[31]and the assessment results [34,36]: (a) Whole composition range;(b) Enlarged part of Fig.6(a);(c) Enlarged part of the Mg-rich side of Fig.6(a),in which the assessment results[34,36]are superimposed;(d) Relevant information of Fig.6(a)-(c).

Fig.7.Calculated isopleth section of the Mg-Gd-Y ternary system at w(Y)/w(Gd)=3 compared with the available experimental data[31]and the assessment results [34,36]: (a) Whole composition range;(b) Enlarged part of Fig.7(a);(c) Enlarged part of the Mg-rich side of Fig.7(a),in which the assessment results[34,36]are superimposed;(d) Relevant information of Fig.7(a)-(c).
The comparisons of the calculated isopleth sections,atw(Gd)/w(Y)=3,1 and 1/3,with the available experimental data from Ref.[31]are shown in Figs.5(a)-(b),6(a)-(b) and 7(a)-(b),and those with the previous thermodynamic assessment results [34,36]are shown in Figs.5(c),6(c) and 7(c).Compared with the previous assessments from Refs.[34,36],the present calculated result can better reproduce the experimental measurements,especially for the regions of the singlephase and the two-phase equilibria [31].
The calculated isopleth sections at 2 and 7 wt.% Y are shown in Fig.8(a) and (b),respectively.The available experimental values and the corresponding calculated data for the phase transformation temperatures from Ref.[35]are also demonstrated in Fig.8(a) and (b).

Fig.8.Calculated isopleth section of the Mg-Gd-Y ternary system with different Y content compared with the available experimental data [35]: (a) 2 wt.%Y;(b) 7 wt.% Y.
Fig.9 shows the simulation results of the solidification processes of three as-cast alloys Mg-10Gd-5Y,Mg-7.5Gd-7.5Y and Mg-5Gd-10Y (wt.%) in Ref.[37],using the present obtained thermodynamic parameters as well as the Scheil solidification model provided by the Pandat software package [43].Scheil solidification assumes that no diffusion occurs in the solid phases,that the composition of liquid phase is uniform(infinite diffusivity in liquid) and that local equilibrium at the solid-liquid interface is always maintained [44,45].The three as-cast alloys have a similar solidification process.α(Mg) solidifies firstly from liquid phase,followed by the two-phase eutectic ofα(Mg)+Mg24Y5and a very small amount of threephase eutectic ofα(Mg)+Mg24Y5+Mg5Gd.In the solidification process reported by Ref.[37],α(Mg) and Mg24Y5are observed experimentally,while Mg5Gd is not detected in the as-cast and as-solidified microstructures due to its low volume fraction.
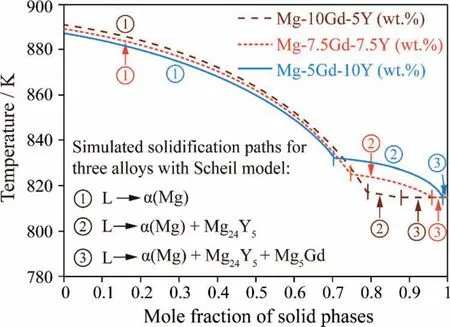
Fig.9.The simulation results of solidification processes for three as-cast alloys Mg-10Gd-5Y,Mg-7.5Gd-7.5Y and Mg-5Gd-10Y (wt.%) from Ref.[37].

Fig.11.The evolution of the metastable phase equilibrium between the disordered HCP_A3 and the ordered Mg7M with increase of temperature in the Mg-Gd-Y ternary system: (a) at 473 K;(b) at 773 K;(c) at 923 K.
5.2.Metastable phase relations of HCP_A3 and D019/Mg7M
The evolutions of the metastable phase equilibria between the stable disordered HCP_A3 and the metastable ordered D019/Mg7M at different temperatures are calculated by using the presently optimized thermodynamic parameters,as shown in Figs.10 and 11.It is observed that the ranges of the HCP_A3+D019and HCP_A3+Mg7M twophase regions decrease with increase of temperature.For the HCP_A3+D019two-phase region in this ternary system,the temperature corresponding to the disappearance of the two-phase region is 1156 K at which the HCP_A3+D019two-phase region reaches the highest temperature in the Mg–Gd binary system.Similarly,for the HCP_A3+Mg7M twophase region in this ternary system,the temperature corresponding to the disappearance of the two-phase region is 1072 K at which the HCP_A3+Mg7Y two-phase region reaches the highest temperature in the Mg–Y binary system.
Fig.12 shows the calculated Gibbs free energies of the stable disordered HCP_A3 and the metastable ordered D019and Mg7M alongx(Y)=0.006 of the Mg–Gd–Y ternary system at 473 K,indicating the positive thermodynamic driving forces for D019and Mg7M to precipitate.

Fig.12.Calculated Gibbs free energies of the stable disordered HCP_A3 and the metastable ordered D019 and Mg7M along x(Y)=0.006 of the Mg-Gd-Y ternary system at 473 K.
5.3.Influencing factors of nucleation resistance
5.3.1.Elastic strain energy
The extensive literature investigations indicate that in the Mg–Gd and the Mg–Y binary systems the interfaces of(D019-type GP zones)/α(Mg),Mg7Gd/α(Mg) and Mg7Y/α(Mg) are all treated as the coherent type [23,26,27].In the Mg–Gd–Y ternary alloys,some experiments have also verified the coherent interfaces of (D019-type GP zones)/α(Mg) [11,13]andβ’-Mg7M/α(Mg) [7,11,13,24,25].
Generally,for the coherent interfaces,the elastic strain energy is greater than the phase boundary energy and is the major factor of the nucleation resistance.Therefore,the elastic strain energy is mainly considered for GP zones (D019-type)andβ’-Mg7M in the present work.
Two commonly used simple equations for calculating coherent elastic strain energy proposed by Porter and Easterling and Russell (cited by Ref.[21]),respectively,are as follows:
where,ΔGsis the total coherent elastic strain energy,Gis the shear modulus of theα(Mg) matrix,εiis the lattice misfit between theα(Mg) matrix and the precipitated phase,amandapare the lattice parameters of theα(Mg) matrix and the precipitated phase,respectively.Vmis the molar volume of the precipitated phase,is the mean Young’s modulus of theα(Mg) matrix and the precipitated phase.Eq.(13) is a formula given under the assumption that Poisson’s ratio for the general metals isν≈0.3.
Since the calculated elastic strain energiesσESof the GP zones (D019-type)/α(Mg) and Mg7Gd/α(Mg) in the Mg–Gd system as well as the Mg7Y/α(Mg) in the Mg–Y system are 28.34,6.02 and 4.02 J/mol,respectively,which are very small relative to the big thermodynamic nucleation driving forces 1008.59,906.98 and 526.03 J/mol,respectively [21,22],the elastic strain energiesσESof the GP zones(D019-type)/α(Mg)andβ’-Mg7M/α(Mg) in the binary and the ternary systems are ignored.
5.3.2.Phase boundary energy
The interfaces ofβ1-Mg3Gd/α(Mg) andβ-Mg5Gd/α(Mg)in the Mg–Gd binary system are respectively treated as the semicoherent and incoherent types [27],and the interface ofβ-Mg24Y5/α(Mg) in the Mg–Y binary system is considered as the incoherent type [29].However,both the interfaces ofβ1/α(Mg)andβ/α(Mg)are all reported as the incoherent type in the Mg–Gd–Y ternary system [7,28,29].In addition,the interfaces of Mg2Gd/α(Mg) and Mg2Y/α(Mg) are also the incoherent type.
As an approximation,the incoherent interfacial energy is assumed as a mean value of the grain boundary energy of the precipitated phase and that of theα(Mg) matrix at aging temperature [46,47].Under this assumption,the expression of the incoherent interfacial energy is presented as follows:
where,γp/α(Mg)is the phase boundary energy in J/m2of the incoherent interface between the precipitated phase and theα(Mg) matrix.γss-pandγss-α(Mg)are the grain boundary energy of the precipitated phase and that of theα(Mg) matrix,respectively,in J/m2.
5.3.3.Grain boundary energy
The grain boundary energy is used for calculating the incoherent interfacial energy as shown in Eq.(16)and for calculating the nucleation resistance deduction of the heterogeneous nucleation,since grain boundaries are favorable nucleation sites as illustrated in Fig.13(b).

Fig.13.The schematic diagrams of the plate precipitates and the α(Mg) matrix: (a) Morphology and size of the homogeneously precipitated plates on {100}α and {110}α prismatic planes [1,51];(b) Heterogeneously precipitated plate on the grain boundary of the α(Mg) matrix.
The expression of the grain boundary energy derived from the size-dependent model based on melting temperatureTmand the Gibbs-Thomson equation is as the following [48]:
where,ris the atomic radius in the specific crystal lattice of the precipitated phase,andΩis the equivalent atomic volume of a unit cell and equals to the ratio of the volume (Vcr) of the unit cell to the numbers of atoms (Ncr)in the unit cell.Ris the gas constant,8.314 J/(mol·K),Vmis the molar volume of the crystal,Vm=NAΩ(NAis the Avogadro constant,6.022 × 1023mol-1),ΔHmis the bulk melting enthalpy calculated by the present thermodynamic optimization parameters at the aging temperature for the typical alloy compositions,andΔSvibis the vibrational entropy in overall melting entropy,ΔSvib≈ΔSm=ΔHm/Tmfor all sorts of other crystals except semiconductors [48].Eq.(17) is used to calculate the grain boundary energy of each precipitated phase as well as that of theα(Mg)matrix.
When the grain boundary energy and the phase boundary energy are calculated for the metastable and the stable incoherent precipitated phases,the solubilities of the third element(Gd or Y) are considered.Taking Mg-2.1Gd-0.6Y (at.%) alloy as an example,the calculated values of the grain boundary energy and the phase boundary energy of the metastable and the stable incoherent precipitated phases at 473 K as well as the parameters used are summarized in Table 4.It is worth noting that if the calculated thermodynamic driving force of a phase is negative such as the phase MgM,it is impossible for this phase to precipitate.Therefore,the grain boundary energy and the phase boundary energy of this phase needs not to be calculated.
5.3.4.Converting the contributions of the phase boundary energy and the grain boundary energy from “J/m2” to“J/mol”
The phase boundary energy is given in the unit of “J/m2”shown in Table 4.In calculating the nucleation resistance,the energy of “J/m2” needs to be converted into that of “J/mol”.The latter is the average phase boundary energy to one mole atoms of the precipitated phase and is related to the surface area and the volume of the precipitated particle.
In the Mg–Gd–Y ternary system,most of the precipitated phases,such as Mg3Gd,Mg5Gd and Mg24Y5,are of the plate morphology,as illustrated in Fig.13(a).The determination of the thicknesshand the radiusris necessary for obtaining the surface area and the volume of the precipitated particle.
For the homogeneously precipitated plates with the radiusrand the thicknessh,as shown in Fig.13(a),the converting expression of the phase boundary energy is as the following:
where,AandVare the total area and the volume of the plate precipitated phases,respectively.Generally,the diameter of a plate structure is much bigger than its thickness,2r≫h,Eq.(19) can be given as follows:
The determination methods of the thicknesseshof the phases Mg3Gd,Mg5Gd and Mg24Y5are the same as those of Refs.[21,22],respectively.However,for the phases Mg2Gd and Mg2Y,since the orientation relationships of Mg2Gd/α(Mg) and Mg2Y/α(Mg) as well as their respective habit planes and morphologies have not been reported,therefore,his assumed theoretically based on the number of atomic layers.A typical grain boundary thickness is assumed to be 3–4 atomic layers [52,53].On this basis,the inner grain thickness can be assumed to be at least 4 atomic layers.Thus,the critical thickness value for a precipitated phase is considered to be the sum of the two side boundary layers (4 layers for each side) and the inner grain layers(5 layers),totally 13 atomic layers.Furthermore,his treated as the product of the number of atomic layers and the interplanar spacing corresponding to the close-packed plane of crystal structure.According to the crystal lattice parameters[54,55],the interplanar spacings of the Mg2Gd and the Mg2Y are d(111)=0.4951 and d(0001)=0.4595 nm,respectively.Then,the estimated critical thickness of the Mg2Gd and the Mg2Y are 4.951 and 4.595 nm,respectively.The converted phase boundary energies in J/mol of the precipitated phases of the Mg–Gd–Y ternary system are listed in Table 5.
For the heterogeneous precipitation as shown in Fig.13(b),the grain boundaries are the favorable precipitation sites and the precipitation at the grain boundary can reduce the resistance for nucleation.The grain boundary energy in J/m2of theα(Mg) matrix averaged to one mole of the precipitated phase in J/mol can be given by the following expression:
where,A0is the area of the precipitation site.The grain boundary energy of theα(Mg) matrixγss-α(Mg)is given in Table 4.h,VandVmin Eq.(21) are the same as those of in Eqs.(16)–(20).The converted grain boundary energies in J/mol of theα(Mg) matrix corresponding to the metastable and the stable incoherent precipitated phase are also listed in Table 5.
5.4.Thermodynamic and effective driving force for nucleation
The effective nucleation driving force DFeffectiveis considered as the difference between the thermodynamic driving force DFthermodynamiccalculated by the present thermodynamic parameters and the nucleation resistance NRnucleationfor the precipitated phases of the Mg–Gd–Y ternary system,as follows:
Three different types of influencing factors of nucleation resistance need to be taken into account,which are the elastic strain energyσES,the phase boundary energyσp/α(Mg)and the grain boundary energy of theα(Mg) matrixσGB.The nucleation resistance NRnucleationcan be expressed by the following formula:
where,σESis the elastic strain energy and can be calculated by Eqs.(13)–(15).σp/α(Mg)is the converted phase boundary energy and can be calculated by Eq.(20).AndσGBis the converted grain boundary energy and can be calculated by Eq.(21).
For the heterogeneous nucleation,the grain boundaries are the most favorable sites,where for each of the precipitated particles the grain boundary of theα(Mg) matrix is replaced by the phase boundary between theα(Mg) matrix and the precipitated particle,as shown in Fig.13(b).
For the homogeneous nucleation,the particle precipitation can occur everywhere,not only along grain boundaries but also inside grains.The interfacial energyσp/α(Mg)and the elastic strain energyσESare the major contributors of the nucleation resistance.
For the three typical Mg-Gd-Y ternary alloys,Mg-2.1Gd-0.6Y,Mg-2.9Gd-0.8Y and Mg-0.992Gd-0.585Y(at.%),the nucleation driving forces of the precipitated phases from the supersaturatedα(Mg) are calculated.Fig.14 illustrates the thermodynamic driving forces and the effective driving forces of various precipitates.It should be pointed out that the positive effective nucleation driving force is necessary for a phase to precipitate.According to Fig.14,the predicted precipitation sequences of the typical Mg-Gd-Y alloys,Mg-0.992Gd-0.585Y (at.%) aged at 448 K [13]and Mg-2.1Gd-0.6Y [14–17]and Mg-2.9Gd-0.8Y (at.%) aged at 473 K [15,16,18,19],are the same as the following:

Fig.14.Nucleation driving forces of the precipitated phases from the supersaturated α(Mg) of the three typical Mg-Gd-Y ternary alloys.
The above predicted result is consistent with the generally recognized aging precipitation sequence of the Mg-Gd-Y ternary alloy [1,2,13–20].
5.5.Aging hardening stages and aging precipitation sequences of the Mg–Gd–Y ternary alloys
The aging hardening curves of the Mg-2.1Gd-0.6Y (at.%)and Mg-2.9Gd-0.8Y (at.%) alloys aged at 473 K [15,16]and their comparison with the aging precipitation sequences calculated by the effective nucleation driving forces are shown in Fig.15.The satisfied agreement is obtained between the predicted precipitation sequences and the experimentally observed ones during the under and the peak aging stages.In addition,in terms of the effective nucleation driving forces of the GP zones (D019-type) andβ’(Mg7M),the calculated values in the Mg-2.9Gd-0.8Y(at.%)alloy are larger than those in the Mg-2.1Gd-0.6Y (at.%) alloy,as shown in Fig.14.Therefore,the age hardening effect of Mg-2.9Gd-0.8Y (at.%) alloy is superior to that of Mg-2.1Gd-0.6Y (at.%) alloy,considering the strengthening effects of the fine,dispersed and coherent precipitation strengthening GP zones (D019-type) andβ’(Mg7M) in theα(Mg) matrix.
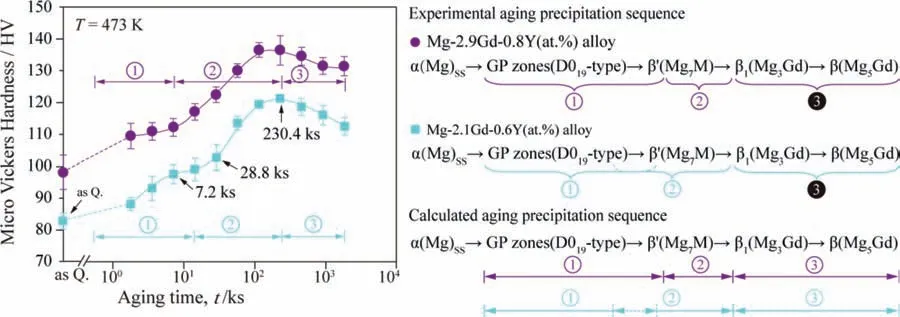
Fig.15.The aging hardening curves of the Mg-2.1Gd-0.6Y (at.%) and the Mg-2.9Gd-0.8Y (at.%) alloys aged at 473 K [15,16],and their comparison with the presently calculated aging precipitation sequences.
Fig.16 illustrates the aging hardening curves of the Mg-0.992Gd-0.585Y (at.%) alloy aged at temperatures of 448,473 and 498 K [13],and their comparison with the calculated aging precipitation sequences.The present calculated aging precipitation sequence of 448 K is in good agreement with the experimental observation result.The precipitated phases during the over aging stage are composed ofβ’,β1andβ.In this stage,theβ’grows and coarsens gradually with the increasing of aging time,and the incoherent phasesβ1andβprecipitate out,leading to the sharp decrease of the alloy hardness.

Fig.16.The aging hardening curves of the Mg-0.992Gd-0.585Y (at.%) alloy aged at 448,473 and 498 K [13],and their comparison with the calculated aging precipitation sequences.
5.6.Design of the Mg-Gd-Y ternary alloys and prediction of the aging precipitation sequences
The calculated maximum solubility ofα(Mg) of the Mg–Gd–Y ternary system is at the temperature of about 815 K.The homogenization treatment is usually at 773 K.That is to say,the compositions of the supersaturatedα(Mg) singlephase solid solution can be designed in the Mg-rich region by reference to the isothermal sections at 815 and 773 K.Sometimes in order to prevent grains from coarsening,the homogenization treatment is carried out in the two-phase region with a very little bit second phase particles,such as Mg5Gd in the Mg–Gd binary alloys and Mg24Y5in the Mg–Y binary alloys,after the as-cast solidification.The aging temperature of the Mg–Gd–Y alloy is generally in the temperature range of 473–523 K,so that the typical alloy compositions are within the two-or three-phase regions.Since the thermodynamic driving force for a given alloy composition decreases with the increase of aging temperature,the typical aging temperature of 473 K is selected to calculate the thermodynamic driving forces for the alloy compositions located in theα(Mg) singlephase region of the isothermal section at the homogenization temperature 773 K and in the two-or three-phase regions at the aging temperature 473 K.
Fig.17(a) presents the calculated isothermal section of the Mg–Gd–Y ternary system at 473 K using the present thermodynamic parameters,and Fig.17(b) is the enlarged view of the Mg-rich corner of the Fig.17(a) and superimposed by the isothermal sections at 815 and 773 K.Moreover,some ternary alloys with different Gd and Y contents are also marked in Fig.17(b),which are selected to predict and compare the available aging precipitation sequences at 473 K.As can be seen clearly from the summary table shown in Fig.17(c),the precipitation sequences of the ternary alloys are the same as those of the corresponding two binary systems in the regions near the Mg–Gd and the Mg–Y sides,while in the middle part,the precipitation sequence transforms from that of the Mg–Gd binary system to that of the Mg–Y binary system.

Fig.17.Calculated aging precipitation sequences for the selected Mg-Gd-Y ternary alloys with different compositions: (a) Calculated isothermal section of the Mg-Gd-Y ternary system at 473 K;(b) Enlarged view of the Mg-rich corner of the Fig.17(a) and superimposed by the isothermal sections at 815 and 773 K,and some reported ternary alloys [13–19,23];(c) Summary of the predicted aging precipitation sequences.
Compared with the previous thermodynamic models of the Mg–Gd–Y ternary system in which only the stable phase relations are considered [33–36],the present thermodynamic assessment takes into account not only the stable phase relations but also the metastable ones.In the meanwhile,the effective nucleation driving force proposed in the present work can simulate the aging precipitation sequences in Refs.[13–19]well.Therefore,the present obtained thermodynamic data as well as the adopted calculation approach can provide important theoretical references for studying the aging precipitation behavior of the Mg–RE alloys and for making full use of the strengthening effects of the metastable precipitated phases.
It is worth mentioning that the present work studies the aging precipitation sequence from a thermodynamic perspective,but the phase precipitation also involves the kinetic process which may have non-negligible impact on the precipitation sequence as well as the morphology,size,amount and distribution of the precipitated phases.The combination of the thermodynamic calculation with the kinetic simulation can play a greater role in the further research.
6.Conclusion
According to the available experimental phase equilibrium relations and aging precipitation sequences,the present re-assessment of the Mg–Gd–Y ternary system is successfully carried out using CALPHAD technique.A set of self-consistent thermodynamic parameters has been obtained.The nucleation resistance of the elastic strain energies for the coherent interfaces,(D019-type GP zones)/α(Mg) and Mg7M/α(Mg),and those of the phase boundary and grain boundary energies for the incoherent interfaces,β1-Mg3Gd/α(Mg),β-Mg5Gd/α(Mg),β-Mg24Y5/α(Mg),Mg2Gd/α(Mg) and Mg2Y/α(Mg) are specially taken into account.
The effective nucleation driving force obtained by subtracting the nucleation resistance from the thermodynamic driving force is adopted to predict the aging precipitation sequence of alloys.With the present assessed thermodynamic parameters and the adopted calculation approach,the calculated stable and metastable phase diagrams as well as the aging precipitation sequences are in good agreement with the reported experimental data.Furthermore,the present study predicts the transformation of the precipitation sequences from the Mg–Gd binary side to the Mg–Y binary side.
Declaration of competing interest
None.
Acknowledgements
The authors would like to acknowledge the National Key Research and Development Program of China (No.2016YFB0701201) and the National Natural Science Foundation of China (No.52071011) for the financial supports.Thanks to the CompuTherm LLC for supplying Pandat Software and Dr.Shuanglin Chen for proofreading the manuscript.
Appendix A
Appendix A
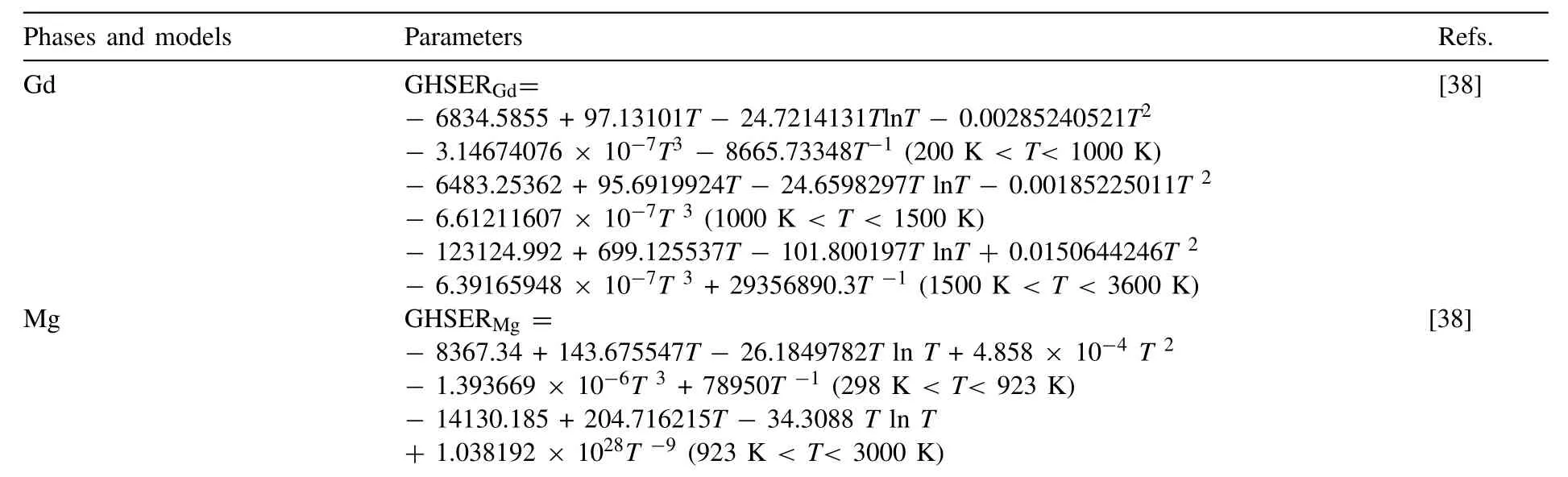
Appendix AThe optimized parameters of the Mg-Gd-Y ternary system a.
 Journal of Magnesium and Alloys2023年7期
Journal of Magnesium and Alloys2023年7期
- Journal of Magnesium and Alloys的其它文章
- Recent progress in MgB2 superconducting joint technology
- “Smart” micro/nano container-based self-healing coatings on magnesium alloys: A review
- Recent advances using equal-channel angular pressing to improve the properties of biodegradable Mg–Zn alloys
- Twin evolution in cast Mg-Gd-Y alloys and its dependence on aging heat treatment
- Effects of Ce content on the modification of Mg2Si phase in Mg-5Al-2Si alloy
- Solute drag-controlled grain growth in magnesium investigated by quasi in-situ orientation mapping and level-set simulations
