Solute drag-controlled grain growth in magnesium investigated by quasi in-situ orientation mapping and level-set simulations
Risheng Pei ,Yujun Zho ,Muhmmd Zuir ,Sngong Yi ,Tll Al-Smmn
aInstitut für Metallkunde und Materialphysik,RWTH Aachen University,52056 Aachen,Germany
b Institute of Materials and Process Design,Helmholtz-Zentrum Hereon,21502 Geesthacht,Germany
c Department of Metallurgical and Materials Engineering,Faculty of Chemical,Metallurgical &Polymer Engineering,University of Engineering &Technology (UET) Lahore,Pakistan
Abstract Critical properties of metallic materials,such as the yield stress,corrosion resistance and ductility depend on the microstructure and its grain size and size distribution.Solute atoms that favorably segregate to grain boundaries produce a pinning atmosphere that exerts a drag pressure on the boundary motion,which strongly affects the grain growth behavior during annealing.In the current work,the characteristics of grain growth in an annealed Mg-1 wt.%Mn-1 wt.%Nd magnesium alloy were investigated by advanced experimental and modeling techniques.Systematic quasi in-situ orientation mappings with a scanning electron microscope were performed to track the evolution of local and global microstructural characteristics as a function of annealing time.Solute segregation at targeted grain boundaries was measured using three-dimensional atom probe tomography.Level-set computer simulations were carried with different setups of driving forces to explore their contribution to the microstructure development with and without solute drag.The results showed that the favorable growth advantage for some grains leading to a transient stage of abnormal grain growth is controlled by several drivers with varying importance at different stages of annealing.For longer annealing times,residual dislocation density gradients between large and smaller grains are no longer important,which leads to microstructure stability due to predominant solute drag.Local fluctuations in residual dislocation energy and solute concentration near grain boundaries cause different boundary segments to migrate at different rates,which affects the average growth rate of large grains and their evolved shape.
Keywords: Magnesium alloys;Grain growth;Quasi in-situ EBSD;Level-set simulation;Solute drag;Dislocation density gradient.
1.Introduction
It is well-known that the mechanical properties of metallic materials are closely related to grain size and crystallographic texture.A fundamental understanding of grain growth during annealing treatments is therefore of great significance to control and design the material’s microstructure for improved combination of strength and ductility.Grain growth is commonly classified into normal and abnormal grain growth [1].In the former,the size of each grain increases uniformly resulting in a self-similar grain size distribution,whereas in the latter,a few very large grains grow preferentially,eclipsing their fine-grained neighbors.Traditional interpretation of abnormal grain growth has been mostly based on Zener pinning of second-phase particles on grain boundaries [2–9].Although a considerable amount of research has been devoted to investigating abnormal grain growth in different materials systems,the mechanisms for the transition from normal to abnormal growth behavior in the absence of pinning particles are not entirely clear.Because solute elements segregate to grain boundaries (GB) in order to reduce the free energy of the system,they impose a drag pressure on the boundary during boundary migration.This is known as solute drag,which can drastically reduce the mobility of grain boundaries during recrystallization and grain growth processes [10].Since both zener and solute drag impede the motion of grain boundaries,the latter can play a similar role in inducing abnormal grain growth.
In Fe-Si alloys,which commonly exhibit selective growth of {011}<100>Goss-oriented grains,abnormal growth was proposed to occur through a solid-state wetting mechanism associated with sub-boundaries of very low misorientations<1°[11–15].These sub-boundaries have particularly low energies,and thus they increase the probability of favorable growth by solid-state wetting as opposed to other grains of less evident anisotropy in their boundary energy.As a result,Goss grains containing a sufficient fraction of sub-boundaries after primary recrystallization can grow abnormally without any mobility and/or energy advantage assigned to their boundary with the matrix grains.
The grain boundary (GB) velocity is a key parameter that governs the growth behavior.It is dependent on the boundary mobility and energy,considering that the boundary curvature is the only acting driving force.For abnormally large grains to sustain a growth advantage over the fine-grained matrix,it is often argued that the respective microstructure has anisotropic grain boundary properties [16].This can be,for example,the case of a polycrystal with increased frequency of coincidence site lattice (CSL) relationships [16–19].In hexagonal materials,the ∑13 (27.8°<0001>) and ∑11 (35.1°<0001>) boundaries have been frequently reported in the context of selective growth due to their low energy and high mobility as compared to other random high angle boundaries [17–19].In this regard,the interaction between solutes and grain boundaries strongly affects the boundary mobility by means of solute drag.For this reason,an often-observed higher mobility for CSL boundaries is believed to arise from a decreased tendency to solute segregation owing to their dense packing of atoms.
In cases of enhanced solute segregation to grain boundaries on the basis of a large size misfit between the matrix and solute atom,solute drag is suggested to amplify the growth advantage of certain grain orientations over others [20–22].For example,in magnesium alloys containing small additions of rare earth (RE) elements,the formation of weak off-basal textures is favored by the suppression of boundary migration via solute drag [20].In this regard,the growth rate of recrystallizing grains with a basal texture can be much slower relative to the rapid growth of non-basal grains,benefiting from the higher mobility of their high-misorientation boundaries [20].Achieving a topological advantage after completion of recrystallization,i.e.larger sizes and higher number of next neighbors can grant the respective non-basal boundaries a sustained growth advantage during subsequent grain growth[23].It is therefore important to mention that any differences in the growth rates of growing grains can be intensified by the pinning effect of solutes decorating the grain boundaries.This is a situation that can lead to abnormal grain growth development,as was observed experimentally and by means of level-set computer simulations [23].
A similar observation was reported earlier by Kim and Park who performed phase field simulations to model grain growth under conditions of solute drag [24].They were able to establish that abnormal grain growth can be induced by solute drag in a two-dimensional system without additional effects,such as texture,anisotropy of GB properties,or grain size advantage.They also demonstrated how the grain growth mode can change depending on the level of solute diffusivity.Below a critical diffusivity value (1 × 10-13m2/s) the GB kinetics,represented in terms of the relationship between the GB velocity and driving pressure,reveals two regimes of dragged migration (slowly growing matrix grains) and free migration(rapidly growing abnormal grains),adapted from the study by Lücke and Stüwe [25].The authors concluded that the grains growing abnormally were the ones satisfying a criterion of a large size and small next neighbors since the driving force for grain growth was given by 1/
The current work is a systematic investigation of the grain growth behavior in an extruded and subsequently annealed Mg-1Mn-1Nd (wt.%) magnesium alloy (hereafter MN11).This alloy was chosen due to its technical relevance and promising corrosion and mechanical properties.Mn addition is known to improve the forming behavior of magnesium alloys during thermomechanical processing.It can also refine the microstructure due to the formation of insoluble,nano-sizedα-Mn particles,which limits the grain size of the dynamically recrystallized grains and contributes to enhancing the yield strength of the material [28–30].Nd addition can also refine the grain size but contributes more importantly to weakening the texture and reducing the problematic yield stress asymmetry in tension and compression[31–35].The grain growth development in the investigated MN11 alloy was studied via quasi in-situ electron backscatter diffraction (EBSD) mappings obtained at different annealing times and level-set computer simulations.Systematic analysis of the evolution of local and global microstructure characteristics during annealing revealed that the GB curvature,residual dislocation density gradient (DDG) remaining after recrystallization,and solute drag control the velocity of GBs,and hence,the growth behavior.These aspects were introduced in the level-set simulations by different combinations in order to discuss their role in the evolution of the real microstructure during annealing.Complementary atom probe tomography (APT) measurements were utilized to examine the segregation behavior at selected boundaries of large/small vs.small/small grains.The residual sum of squares was applied to assess the variance in the experimental and simulated data sets.The results showed that the observed favorable growth for some grains is controlled by several drivers of different importance at different stages of annealing.With increasing annealing time,stabilization of the microstructure is attributed to a reduction of dislocation density gradients between large and small grains,which at a certain point cannot overcome the drag force from segregated solutes at grain boundaries.The modeling approach has therefore shown a promising potential to incorporate various key aspects of grain growth with comprehensive complexity and reasonable accuracy.
2.Experimental and modeling procedures
2.1.Material
The studied MN11 alloy contained 1.05 wt.% Mn and 1.14 wt.% Nd.After casting and homogenization heat treatment,the alloy was extruded at 300 °C and a ram speed of 2.5 mm/s to a final diameter of 8.0 mm achieving an extrusion ratio of 1:38 [32,33].For the grain growth experiments using quasi-in-situ EBSD mapping,an electropolished specimen was heat treated at 450 °C for different durations (0.5 h~6 h)under a protective argon atmosphere to avoid surface oxidization.
2.2.Microstructure characterization
After mechanical grinding and polishing,specimens for EBSD measurements were electro-polished in AC-2 reagent at -20 °C for 90 s using a voltage of 20 V.EBSD measurements (step size of 0.6 μm) were performed in a FEI Helios 600i dual-beam microscope operated at 20 kV.Fiducial marks on the surface of the sample were used to ensure collecting EBSD data from the same area following each annealing step.After each annealing step,the same specimen was rapidly quenched in water and repolished in Struers OP-U suspension for 30 s to improve the surface quality for the next EBSD scan.The thickness reduction after the intermediate polishing steps was less than 1 μm.Analysis of the collected quasi-insitu EBSD data was carried out in the MTEX toolbox [36].Elemental distributions of solute atoms at the grain boundaries were characterized using 3D APT in a Local Electrode Atom Probe 4000X HR with laser-pulsing mode (ultraviolet laser with wavelength: 355 nm,pulse energy: 30 pJ and frequency: 125 kHz).During the measurements,the temperature was set to 30 K.The lifted APT tips with the targeted grain boundaries were sharpened via a coordinated process of transmission Kikuchi diffraction EBSD (TKD-EBSD) and focused ion beam (FIB) milling at 30 kV and 5.5 nA beam current to ensure a proper position of the GB within the APT tips[22].The milling process included a final low-energy step at 2 kV.The evaporated tips were reconstructed and analyzed using the IVAS 3.8.2 software package from Cameca.
2.3.Level-set modeling setup
The utilized level-set model in this work is an open source code [37]that can predict the temporal evolution of structural interfacial elements of the microstructure considering a broad range of grain growth scenarios [38].Recently,it has been successfully implemented to model the grain growth behavior in pure Mg [39]and Mg alloys [23].
The growth rate of the migrating boundary (v) at timetis proportional to the grain boundary mobility (m) and the driving force (p):
Heremeffis the effective boundary mobility taking the finite mobility of triple junctionsmTJinto account [40]:
WheremGBrepresents the average mobility of the adjacent grain boundaries to the triple junction.In terms of dimensionality,it is noted thatmTJis of one lower spatial dimension thanmGB[41].It is also noted that Eq.(2)was exclusively applied to triple junction regions defined by sectors of lengthdsthat were utilized in a segmentation step of grain boundaries to discriminate between triple junction and grain boundary regions.Details of the segmentation approach of the grain boundary are found in [40].In the current study,a ratio of
For low angle grain boundaries (LAGB,θ<15°),mGBwas taken as a function of the misorientation angle:
For high angle grain boundaries (HAGB,θ >15°),the mobility is assigned a constant valuemmax=4.3 × 10-14m4/Js[42].
In the current simulations,the evolution of the grain growth microstructure is investigated for different combinations of driving and pinning forces,comprising the effects of local curvature (pc),residual dislocation density gradients(pDDG) and solute drag (pSD):
κis the local curvature of a boundary segment andγis the boundary energy.For HAGB,γis assigned a constant valueγmax=0.5 J · m-2.For LAGB,it is dependent on the boundary misorientation angle in accordance with the Read-Shockley model [43].
According to Cahn[50],the drag force on the grain boundary due to its interaction with solute atoms is given by
Wherenis the atomic density in the boundary plane,c(x)the solute concentration profile at the boundary andEthe interaction force between the solute and the grain boundary,which varies with the distancexfrom the boundary located atx=0.The integration range of±∞does not refer to infinite distances but rather to positions in the bulk that are far enough from the boundary region.According to[24],for a dilute ideal solution and dragged boundary migration at low velocities,the concentration profile becomes close to the equilibrium segregation profile,and hence Eq.(7) can be approximated as
From Eq.(8) it is obvious that the drag force depends on the velocity of the migrating boundaryVrelative to the solute diffusivityD.cGBandcMare the equilibrium solute concentrations at the grain boundary and in the matrix,respectively,which were experimentally determined from the APT data in Fig.6.2ξcorresponds to the boundary thickness,which is usually the size of a few atomic layers but can be also approximated (although not precisely) from the APT data.β=Vm/RT,whereVmis the molar volume of solute.By adoptingD=8.7 ×10-15m2s-1[51],V=0.14 μm s-1[24],β=8.3 × 10-9m3J-1withVm=20.58 cm3mol-1andT=298 K [52],2ξ=2 nm,cGB=0.015 andcm=0.0018,the drag force can be estimated asPSD~5 ×104Jm-3.It must be emphasized that this estimation is not accurate since no real boundary velocity and molar volume of Nd at 450 °C are measured.For simplicity,PSDwas kept constant during the simulations.
The starting microstructure that was used as input for the simulations corresponded to annealing condition of 450 °C/ 30 min.Table 1 represents the different conditions applied in the simulations in order to understand their role in the experimentally obtained grain growth microstructure.

Table 1The different combinations of driving forces applied in the level-set grain growth simulations and the corresponding expressions for calculating the grain boundary velocity.
3.Results
3.1.Development of global microstructure characteristics
The evolution of grain size distribution and texture during annealing at 450 °C for different durations was tracked by quasi-in-situ EBSD mapping,as shown in Fig.1 in terms of inverse pole figure maps with respect to the extrusion direction (IPF-ED) and corresponding area fraction vs.lnDplots(Ddenotes the grain diameter)in Fig.2.In the early annealing stages up to 2 h,abnormal grains continued to emerge out of areas,in which the matrix grains seemed to exhibit a uniform size distribution(cf.outlined grains by white circles in Fig.1b and c).The two abnormal grains indicated by arrows in these maps maintain their favorable growth condition by consuming the surrounding fine-grained matrix.A comparison of the grain size distributions after 0.5 h and 2 h annealing durations revealed a loss in self-similarity indicated by an increase in the standard deviation (breadth) of the fitted distribution (Fig.2a-c).The mean grain size increased from 11.3 ± 1.69 μm to 17±1.93 μm.It was also obvious that the area fraction of the abnormally large grains with sizes between~55 μm (lnD=4)and~90 μm (lnD=4.5)was increased.With further annealing up to 4 h,the smaller matrix grains seemed to coarsen (outlined regions by black circles in Fig.1d),and the mean grain size climbed from 17 μm to 29 μm.Correspondingly,the grain size distribution in Fig.2d depicted further broadening fromσ=1.93 μm toσ=2.26 μm (σ: Standard deviation of the fitted normal grain size distribution) indicating that an abnormal growth behavior still existed [8,53].

Fig.1.Quasi-in-situ EBSD orientation mapping of the microstructure evolution in the same region of a MN11 alloy specimen annealed at 450 °C for different durations between 0.5 h and 4 h (a-d).The EBSD maps correspond to IPF color coding relative to the extrusion direction ED.The inserted ED-IPFs reveal a<112>‖ED rare-earth texture common for extruded Mg-Mn-RE alloys [54].
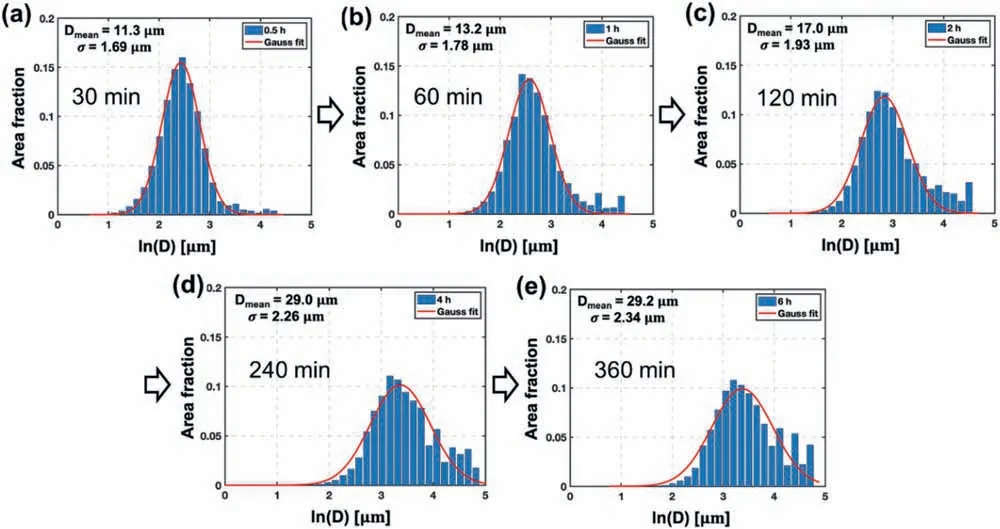
Fig.2.Grain size distributions for the annealed samples at 450 °C up to 6 h calculated from the EBSD maps shown in Fig.1.The grain size data was fitted with a distribution fit (red curve) to acquire the breadth of the distribution.
For longer annealing durations up to 6 h,the microstructure,grain size distribution and texture did not change significantly.This observation suggests that the detected coarsening of the finer matrix grains enables them to catch up with the faster growing large grains,thereby preventing further broadening of the distribution.This type of ‘transient’behavior of abnormal grain growth was observed previously in [16].As shown by the attached IPFs,the rare earth extrusion texture<112>‖EDis maintained during grain growth.
3.2.Development of local microstructure characteristics
To investigate the favorable growth conditions of the large grains at a local level,multiple areas of such grains and their surrounding matrix were tracked throughout the EBSD measurements for a systematic analysis of their local characteristics as shown in Fig.3.For example,Grain 8 in Fig.3b grew rapidly from~30 μm (measured after 0.5 h annealing)to~66 μm (after 2 h).After 6 h,the size of this large grain reached~80 μm,which indicates a decrease of its growth rate.By comparison,the average grain size of Grain 8 next neighbors increased from~7 μm to~21 μm throughout all annealing steps.The black arrows mark the growth directions,in which the boundary segments of Grain 8 were seen to migrate and thereby consume the surrounding matrix in the next annealing step.Interestingly,certain boundary segments (e.g.S1 and S2 in Fig.3b) remained more or less stationary during annealing between 1 h and 6 h despite having a concave curvature.The misorientation relationships of these segments are 53°<253>and 11°<32>,respectively.S2 being a low angle boundary is therefore expected to have a low mobility and a resulting low migration velocity.On the other hand,the low velocity of the high angle boundary segment S1 cannot be explained by an orientation-pinning effect.This observation clearly points out that the rapidly growing abnormal grains have a non-uniform boundary migration behavior with important implications for the grain growth kinetics,as discussed later in Section 4.

Fig.3.(a) Example of tracking of individual abnormal grains in an IPF map obtained at 450 °C/ 360 min in order to study the evolution of their (b) local characteristics (grain size and topology) and (c) GND density distribution as a function of annealing duration.The black arrows in (b) indicate the growth directions,where the boundary segments of grain 8 expand in the next annealing step.The delineated boundaries of Grain 8 indicate stationary/ slowly migrating GB segments despite having a concave curvature.
In addition to the evolution of grain topology and misorientation relationships,the variation of GND density within the large grains and their surrounding matrix was tracked with increasing annealing time as shown in Fig.3c for Grain 2.It can be seen that during the first annealing steps (e.g.at 0.5 h)the surrounding matrix of Grain 2 possessed a higher GND density on average (~9.6 ×1013m-2) as compared to the interior of Grain 2 itself (3.5 × 1013m-2).This provides an additional driving force for Grain 2 to grow at the cost of its next neighbors in order to minimize the existing dislocation density gradient.Upon further annealing,Grain 2 is indeed seen to grow and the color coding of the surrounding matrix shows darker tones indicating a corresponding drop in the GND density.When the difference between the GND densities was largely eliminated,Grain 2 was not seen to grow much further.This observation suggests that the effect of dislocation density gradients on abnormal growth is only crucial for the first stages of annealing.This information has proven useful with respect to the simulations,as shown later.
A statistical overview of the analysis explained in Fig.3 on the basis of Grains 2 and 8 is presented in Fig.4 for additional large grains and their surrounding neighbors.This includes the evolution of grains size,average boundary curvature and GND density.The same trend that was explained for Grains 2 and 8 regarding energetic advantages in the boundary curvature and remaining dislocation density after recrystallization can be seen for the other large grains.Fig.4b and c also demonstrate how well the growth rate of the large grains correlates with the existent gradients in the average boundary curvature and dislocation density.When these gradients between the large grains and their neighbors diminish with annealing,the growth rate of all the large grains in Fig.4a is seen to decrease accordingly.

Fig.4.Statistical analysis of the evolution of local microstructure characteristics as a function of annealing duration extracted from the respective quasi-in-situ EBSD maps.Evolution of (a) grain size of the abnormal grains and their direct neighbors (as an average),(b) average boundary curvature,and (c) average GND density.The favorable growth of the abnormal grains is associated with a sudden velocity jump in the v - p relationship (d) adapted from Lücke and Stüwe [25].A combination of favorable gradients in the grain size 1/
3.3.Grain boundary solute segregation
3.3.1.Case 1: GB of an abnormal grain and a small neighbor
Solute segregation to grain boundaries was analyzed by 3D atom probe tomography on a sample annealed at 450 °C for 2 h.Fig.5c shows a reconstructed measured tip containing a segment of a targeted grain boundary between an abnormally large grain and a much smaller neighbor (Fig.5a).Fig.5b is a TKD-EBSD map obtained during the milling process at 30 kV illustrating the misorientation of the grain boundary (52.9°<201>) and its depth from top of the tip.The elemental distributions of Mg,Nd and Mn solute atoms in Fig.5c clearly indicate favorable local enrichment of Nd and Mn on the boundary.Quantitative information in that regard is given in Fig.5d in terms of Mn and Nd concentration profiles across the boundary,extracted from a cubic region of interest (ROI) outlined in Fig.5c.As can be seen,the peak concentration of Nd on the boundary was 2.55 at.% (vs.0.18 at.% in the matrix),and that of Mn 0.62 at.% (vs.0.15 at.%in the matrix).Further analysis also revealed that the segregation behavior in the boundary region was anisotropic as shown by a 2D concentration contour map of Nd,reproduced from the same ROI mentioned earlier (Fig.5e).Apparently,the local segregation concentrations of Nd in the shown y-z plane reveal a strong variation within the GB plane,ranging between 3.0 at.% and 1.2 at.%.
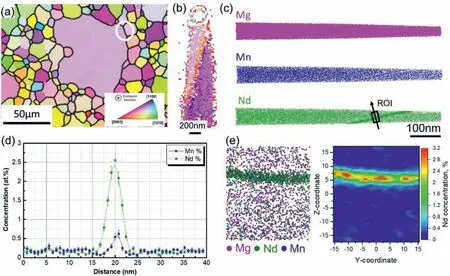
Fig.5.Quantitative analysis of solute segregation at a boundary between an abnormally large grain and a smaller neighbor.(a) IPF orientation map with respect to the extrusion direction showing the targeted GB (misorientation: 52.9°<201>);(b) TKD-EBSD map of the tip before the final low-energy milling step;(c) elemental distributions of Mg,Mn and Nd atoms from the reconstructed tip;(d) solute concentration profiles of Nd and Mn within a cubic ROI outlined in (c);(e) atom distribution and 2D concentration map extracted from the ROI in (c),showing anisotropic segregation of Nd in the GB plane.
3.3.2.Case 2: GB of two small grains
To check whether solute segregation at a grain boundary between two small grains bears important differences in comparison to case 1,another APT tip with a respective GB segment of a very similar misorientation (55.2°<201>) was measured,as shown in Fig.6.The concentration profiles across the grain boundary show evident co-segregation of Nd and Mn in the GB region,similar to what was observed in Fig.5.The peak concentration of Mn at the boundary was 0.55 at.%,which is comparable to that of the other boundary but the GB Nd concentration was somewhat lower than that in this case (1.53 at.% vs.2.55 at.%).Solute segregation in the GB plane was also anisotropic as in the previous case.
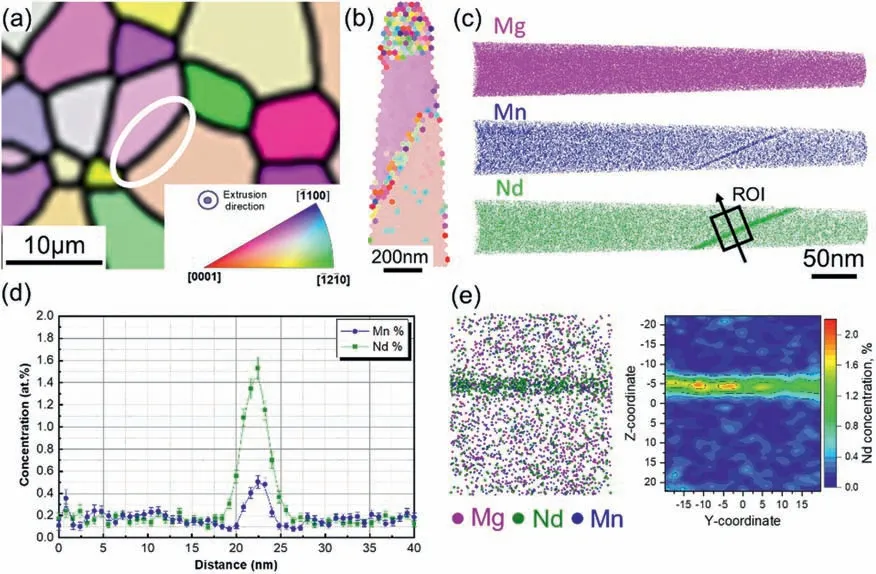
Fig.6.Quantitative analysis of solute segregation at a boundary between two small grains.(a) IPF orientation map with respect to the extrusion direction showing the targeted GB (misorientation: 55.2°<201>);(b) TKD-EBSD map of the tip before the final low-energy milling step;(c) elemental distributions of Mg,Mn and Nd atoms from the reconstructed tip;(d) solute concentration profiles of Nd and Mn within a cubic ROI outlined in (c);(e) atom distribution and 2D concentration map extracted from the ROI in (c),showing anisotropic segregation of Nd in the GB plane.
3.4.Grain growth simulations
For the simulations,the average grain size of all grains was used as a criterion to match the simulation and experimental time steps.A comparison was made between the following characteristics:average grain size of all grains,of large grains,and of small grains,as well as the peak breadth of the Gauss fit of the grain size distribution obtained from EBSD and simulations.A grain with a diameter three times larger than the average of all grains was defined as a ‘large’ grain and the rest of the microstructure as ‘small’ grains.As Fig.7ad show,this comparison was carried out for four different grain growth scenarios comprising different combinations of potential driving forces.The residual sum of squares (RSS)was used to assess the variance between the simulated and experimental results,as shown in Fig.7e.Smaller RSS values indicate a better agreement of the data.

Fig.7.Quantitative comparisons between experiments and simulation outputs using different combinations of potential driving forces for grain growth in the investigated MN11 alloy (a-d).The table in (e) provides the residual sum of squares (RSS) that measures the difference between the simulated and experimental data.The peak breadth refers to the normal fit of the grain size distribution.Italic and underlined values denote the best match between experiment and simulation.SD: solute drag,DDG: Dislocation density gradient.
In the case with only the curvature driving force (Fig.7a),the simulation output of the average grain size of all grains and small grains coincided well with the experimental data.Problems were seen with the prediction of the average size of large grains and the breadth of the distribution.With the introduction of the opposing drag force in Fig.7b,the growth kinetics revealed a limiting grain size of the small grains at~8 μm and the large grains at~48 μm.The calculated RSS of the average grain size of all grains showed a very large variance between the experimental and simulation data.Improvement in the prediction capability of the model was evident after considering different residual dislocation densities(Fig.7c) in accordance with the experimental observations reported in Section 3.2.The best fit was then achieved after introducing all three forces in the simulation,as shown in Fig.7d and e.Fig.8 illustrates the simulated microstructures at different times (represented in terms of IPF maps relative to ED) using that setup,which shows a reasonable agreement between the experimental and modeled microstructure evolution.

Fig.8.Level-set simulations of grain growth microstructures at different time steps: 1 h (b) and 6 h (c) using an experimental annealed microstructure (450 °C/ 30 min) as input (a),and the pc + pSD + pDDG setup (cf.Table 1 and Fig.7).
4.Discussion
As demonstrated by the results,the grain growth behavior in the investigated MN11 alloy can be characterized by an initial stage of abnormal grain growth,which slows down with increasing annealing time.The velocity of grain boundaries is controlled by the interplay between the boundary curvature,gradients in the residual dislocation densities after recrystallization and solute drag.The level of contribution of each of these forces to the microstructure development in terms of a growth advantage varies through the annealing process.It is therefore important to understand their combined influence on the heterogeneous growth behavior in the current alloy.
For solute drag-controlled migration,as in the present case,abnormal growth is suggested to take place once a portion of grain boundaries in the microstructure undergoes a rapid transition from dragged migration to free migration.This is usually associated with a sudden jump in the migration velocity that occurs above a critical driving force [25,50].Phase-field simulations of the growth kinetics under conditions of GB solute segregation [24]showed that the relationship between the driving forcepand the migration ratevof the grain boundary can be influenced by the solute diffusivity.For solute diffusivities lower than a critical value ofD=3 × 10-13m2·s-1,abnormal grain growth can be triggered without any additional advantages from texture,grain size or anisotropy of GB properties.For diffusivities larger than the critical value,grain growth proceeds in the normal mode.In the current work,Nd atoms were the primary segregating species to grain boundaries (Figs.5 and 6) since there was no sufficient solute Mn available after precipitation of nanosized pure Mn particles [32].From diffusion-couple experiments reported in[51],the diffusion coefficient of Nd in polycrystalline Mg at 450 °C is about 10-14m2·s-1,which agrees fairly well with the diffusivity range for abnormal grain growth reported in[24].Since the mode of grain growth under solute drag will depend on the capability of some grain boundaries to break free from the solute atmosphere,grain size (curvature) in the initial microstructure with a uniform size distribution can be an important factor to the process.The chance of having a supercritical driving force to overcome solute drag on the basis of present size advantage will increase considerably if an additional advantage materializes (e.g.through a favorable gradient in the residual dislocation density,as discussed later).For the abnormal mode of grain growth,the initial grain size has to be slightly higher than a critical value,such that only a small fraction of grain boundaries (driven by a supercritical driving force) can overcome the drag effect and grow rapidly relative to the pinned matrix grains.The authors in [24]predicted the respective critical curvature to be close to 18-1μm-1,which corresponds to a grain size of 6 μm using an approximation<κ>=(3d)-1for a two-dimensional system.In the current work,the average grain size of the initial extrusion microstructure prior to the annealing treatments was about 7 μm,suggesting that in addition to the condition of a low diffusivity,the grain size criterion for triggering abnormal grain growth is also satisfied.This is important because the ‘right’ grain size enables the aforementioned supercritical driving force to act only on a small fraction of the grain boundaries in the annealed microstructure.
From Fig.7b,it is evident that the large grains in the simulation using a curvature driving force and solute drag stopped growing after a time equivalent to 2 h of annealing.In experiments,however,the large grains were able to grow further regardless of the pinning effect on the boundaries.It is therefore believed that this difference arises from the lack of an additional driving force in the simulation.As shown in Figs.3c and 4c,the average dislocation densities in the small neighboring grains of the large grains can be up to one order of magnitude higher.This will introduce an additional driving pressure on the boundaries,allowing them to break away from the pinning solute at a larger critical pressure.The relevance of existing dislocation density gradients in recrystallized microstructures was also reported in a previous grain growth study on pure magnesium [39],where the role of DDG in strengthening the (0001)<110>texture component was established.
The grain size distributions of experimental and simulated microstructures are compared in Fig.9 for different annealing times and simulation scenarios as per Fig.7e.The simulation setup with the curvature driving force and solute drag(Fig.7b) was not considered in the comparison since grain growth in the simulation ceased after a short time.Clearly,only the simulated distributions in Fig.9b exhibit a normal growth behavior with self-similarity in terms of the distribution width and height.This can be understood by the absence of solute drag and the additional driving force associated with DDG in the simulations.The introduction of DDG in Fig.9c facilitates the growth of grains with a low GND density causing the grain size distribution to lose its self-similarity with increasing time.However,due to an overestimation in the number and growth rate of these grains the peak height and width of the predicted distributions were inconsistent with those of the experiments.This was refined by additionally accounting for solute drag (Fig.9d),which helped increase the width of the distribution by limiting the number of favorably growing grains with a DDG advantage.The resulting distributions showed an excellent agreement with the experimental ones.
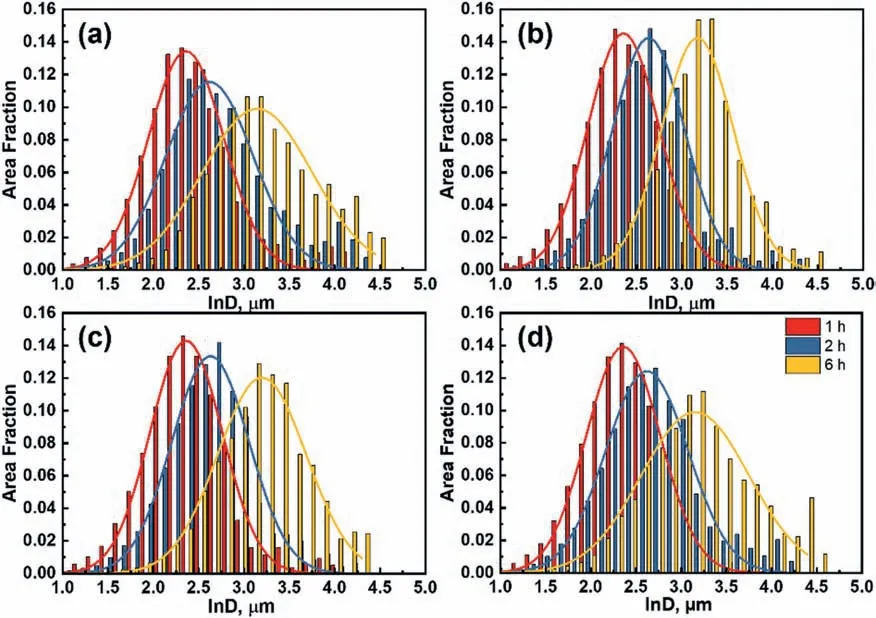
Fig.9.Comparison of grain size distributions obtained from annealing experiments at 450 °C for different times (a) and counterpart level-set grain growth simulations using the curvature driving force (b),the curvature driving force and an additional force from dislocation density gradients (c),both the curvature and DDG driving forces along with solute drag (d).D is the grain diameter.
Fig.10 is a schematic illustration of how the observed growth behavior in the present alloy is controlled by the interplay between boundary curvature,DDG and solute drag.The colors of grains used indicate different levels of the residual dislocation density (blue Fig.10.Schematic illustration explaining the experimental grain growth behavior of the MN11 alloy during annealing at 450 °C.The colors of the grains represent an inhomogeneous distribution of residual dislocation densities throughout the microstructure (blue < orange < red),which act as a driving force.The white dots refer to fluctuations in the distribution of solute atoms at the grain boundaries.These effects lead to non-uniform boundary migration and hence to elongated shapes of the growing grains. Fig.10 also brings into perspective that the migration of grain boundaries is not uniform because of local fluctuations in the forces acting on different boundary segments.Naturally,these boundary segments have different curvature values and are associated with different dislocation density gradients in their adjoining grains,as illustrated in the zoomed areas in Fig.10a and b for grain A and its direct neighbors.Another important source of inhomogeneity with respect to non-uniform boundary migration originates from fluctuations in the solute concentration within the grain boundary plane,as evident in Figs.5e and 6e.Atomistic simulations reported in [22]suggest that the inhomogeneous GB segregation behavior of Nd is linked to local atomic rearrangements within the grain boundaries.All these effects leading to non-uniform boundary migration during grain growth explain why some boundary segments were almost stationary (e.g.grain 8 in Fig.3b),giving rise to uneven grain shapes resembling those of “amoebas”.According to Lin et al.[55],a consequent increase in the fraction of stationary (or even slowly moving) boundaries during annealing can be responsible for the decrease of the average growth rate of the abnormal grains observed after 2 h of annealing at 450 °C.Since the grain growth kinetics are obviously influenced by this behavior,future model development needs to account for anisotropic solute drag and resulting non-uniform migrating velocities of grain boundaries. In this work,the grain growth behavior in an annealed MN11 magnesium alloy was investigated under solute drag using quasi-in-situ EBSD mapping and level-set computer simulations.The following conclusions can be drawn from the results: (i) For short annealing durations,a limited number of grains develops a growth advantage relative to their neighbors,resulting in a transient stage of abnormal grain growth.With increasing annealing time,the growth rate of the abnormal grains subsides leading to a comparable growth behavior to that of the smallgrain clusters.For longer annealing times up to 6 h,the growth of both small and large grain populations ceases,giving rise to a thermally stable microstructure. (ii) The quasi in-situ microstructure evolution as a function of annealing time revealed that the growth behavior of the large grains is not uniform.It was evident that for the same grain some boundary segments continued to migrate while others became stationary despite having a concave curvature.Such non-uniform boundary migration velocities lead to grain morphologies similar to amoebas. (iii) A systematic analysis of the development of local microstructural characteristics during annealing suggests that commencing gradients in the dislocation density remaining after recrystallization are critical in granting the abnormal grains the transient advantage they need to overcome the pinning force of segregated solute at their boundaries.This effect corresponds to a sudden jump in the boundary velocity-driving pressure relationship predicted by the Cahn solute drag model. (iv) The perpetual change of the grain boundary area of shrinking grains entails a redistribution/ accumulation of solute atoms in the vicinity of the growing boundaries in the high velocity regime.This is likely the reason for the higher solute concentration at boundary segments separating large and small grains,as compared to boundary segments between small grains.This is not related to anisotropic segregation due to different boundary characteristics since the targeted grain boundaries had a very similar misorientation axis/angle relationship. (v) Level-set computer simulations carried out in different setups were very helpful in unraveling the effect of different force combinations on the grain growth behavior.With the setup that is most close to the experimental conditions,the model was capable of reproducing the experimental growth behavior.A convincing agreement was not only seen in terms of the developed grain size distribution but also with respect to the evolution of local microstructure statistics.The modeling approach has therefore shown a promising potential to incorporate various key aspects of grain growth with comprehensive complexity and reasonable accuracy.The aspect of local fluctuations in the boundary solute concentration and how it could influence the prediction accuracy of the model should be considered in future development of the current approach. Declaration of competing interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. Acknowledgement The financial support of the Deutsche Forschungsgemeinschaft (DFG),Grant no.AL 1343/7–1,AL 1343/8–1 and Yi 103/3–1 is gratefully acknowledged.
5.Conclusions
 Journal of Magnesium and Alloys2023年7期
Journal of Magnesium and Alloys2023年7期
- Journal of Magnesium and Alloys的其它文章
- Recent progress in MgB2 superconducting joint technology
- “Smart” micro/nano container-based self-healing coatings on magnesium alloys: A review
- Recent advances using equal-channel angular pressing to improve the properties of biodegradable Mg–Zn alloys
- Twin evolution in cast Mg-Gd-Y alloys and its dependence on aging heat treatment
- Effects of Ce content on the modification of Mg2Si phase in Mg-5Al-2Si alloy
- Formation and growth of precipitates in a Mg-7Gd-5Y-1Nd-2Zn-0.5Zr alloy aged at 200 °C
