基于窗口波动模式识别的纺纱过程质量波动异常预警

胡 胜, 陈 臣, 李 文, 汪成龙

(西安工程大学 机电工程学院,西安 710048)

纺纱过程由于其复杂环境及多源信息交互性等特点,其各环节中的成纱质量受到多种质量参数影响,且目前纱线质量控制方法还停留在事后质检的水平上[1],只能发现废品而不能预防废品的产生,其结果直接导致企业的制造成本增加并造成更多经济损失[2]。因此,针对纺纱过程质量波动问题,从早期挖掘异常波动的角度出发,对纺纱过程出现异常波动的时刻及异常原因进行预警分析,及时对纺纱过程稳定性进行判别具有重要意义。

目前,国内外学者围绕异常预警问题主要从以下两种实现方式进行了深入研究并取得一系列成果：一是基于历史数据及先验知识进行健康监测与状态评估实现异常预警。Wu等[3]提出了一种合适的模糊下推自动机控制方法,以实现纱线质量控制。徐继亚等[4]提出了一种基于融合核主元分析与模糊信息粒化的支持向量机预测方法,通过跟踪性能退化指标的变化趋势及波动范围,实现轴承故障预警。为解决单一工序的纺纱质量控制模型难以实现对纺纱质量的精准控制问题,邵景峰等[5]构建了一种基于多工序知识关联的纺纱质量智能控制模型。胡胜等[6]提出一种基于节点敏感波动分析的质量稳定性评估方法,通过计算误差因素的敏感波动率实现异常质量状态的敏感波动分析。刘伟强等[7]提出一种基于脆性度和云模型的健康状态评估方法,在发动机缸盖装配系统评估过程中提供准确及时的状态信息。王梓齐等[8]提出一种基于模糊软聚类和集成的状态监测方法,通过构造健康指数反映齿轮箱的早期故障及其发展趋势。邓丽等[9]提出一种融合数据流时空特征和多分类模型的异常检测算法,对传感器数据流进行异常检测及异常类型识别。严英杰等[10]构建了一种基于滑动窗口和聚类的融合算法,实现对变电设备的异常情况进行检测。倪广县等[11]提出了一种滚动轴承高维随机矩阵的状态异常检测算法。Zeng等[12]提出了基于稀疏贝叶斯学习和假设检验的齿轮箱油温异常检测方法。赵庆兵等[13]设计并开发了一种基于参数自回归算法的用于核电厂关键设备早期预警的方法,通过动态阈值对设备状态进行监测。Zhang等[14]采用多变异状态估计技术构建描述设备正常状态的非参数模型,将状态的滑动窗口相似性作为故障预警的评价标准。另一种是基于数据建模的预测方法,其基本思想是通过分析历史运行数据的关联关系,对后续参数趋势进行短时预测,并设置阈值实现异常预警。Yang等[15]提出一种基于多元回归模型的纺纱质量预测方法,通过大量的纺纱历史数据构建预测模型实现对纱质量的精准预测。王明达等[16]建立基于支持向量机的在线异常预测模型和基于贝叶斯网络的故障诊断模型,在数据采集与监视控制系统(Supervisory Control and Data Acquisition,SCADA)上实现异常判别。董海鹰等[17]构建自回归求和滑动平均模型对风力发电机轴承寿命进行预测。王庆锋等[18]提出一种基于谱距离指标运行可靠性曲线趋势滤波的旋转设备性能退化预测模型,实验表明该方法能够在不依赖专家先验知识的前提下准确预测和追踪旋转设备性能退化趋势的发生和发展。胡胜等[19]提出基于变点识别的纺纱过程质量波动异常预警方法,通过移动窗口分析和多核学习技术对纺纱过程质量特性波动的分布变点进行识别,实现纺纱质量波动预警。

以上研究发现,目前针对生产过程异常预警问题的研究主要集中在设备或零件故障预警及产品质量特性异常监测,而针对纺纱生产过程的质量稳定性问题鲜有研究,在实际的纺织生产过程中,其过程波动稳定性是掌握纱线质量的有效途径,从预防异常影响扩大的角度,及时推断纺纱过程的异常波动进行早期预警和异常溯源分析仍是当前研究的重要方向。基于此,本文在前述研究成果的基础上,重点聚焦纺纱过程中的多质量因素波动异常预警问题,提出一种基于窗口波动模式识别的纺纱过程质量波动异常预警方法,通过均方根误差表征相邻窗口的质量因素波动程度,在引起质量特性波动前实现纺纱过程异常的早期预警,并对异常波动源头进行追溯,最后通过实例验证所提方法的有效性。

1 纺纱过程多质量参数波动表征

1.1 纺纱过程质量波动表征

纺纱过程质量波动异常预警的基础是对多质量监测参数进行波动模式表征。纺纱过程处于正常波动模式时,其监测数据在合理的区间内波动;当出现异常因素时,监测点间的波动幅度及波动趋势会出现显著变化。为有效表征纺纱过程质量波动变化,同时消减随机波动对异常预警结果的影响,本文进行质量波动表征与窗口序列分解。

记m维度样本容量为n的纺纱过程多质量参数序列{xl1,xl2,…,xlm},其质量波动表征流程如图1所示。

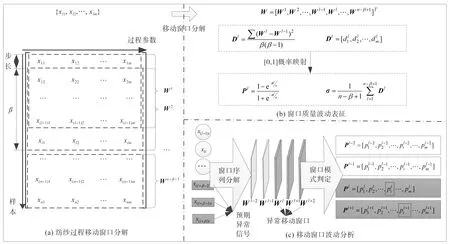
图1 纺纱过程质量波动表征Fig.1 Quality fluctuation characterization in the spinning process

具体步骤如下：

1) 设滑动窗口由目标时刻及前β-1个时刻的监测数据组成,[xli,x(l+1)i,…,x(l+β-1)i]表示监测参数i在β个时刻内的窗口序列,窗口大小为β×m。当新数据产生时,滑动窗口整体向前滑动一个位置,将原窗口最末端的数据删减,并加入新数据,实现滑动窗口的迭代更新。设滑动窗口的宽度为β,窗口每次移动一个时间点,对于n个样本数量的纺纱过程多质量参数序列X共有n-β+1个滑动子窗口,对其采用滑动窗口处理得到窗口状态矩阵,由下式确定。

W=[W1,W2,…,Wl,…,Wn-β+1]T

(1)

式中：Wl表示l时刻形成滑动子窗口。

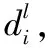
(2)

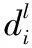
(3)

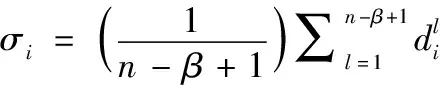
1.2 质量波动窗口序列分解

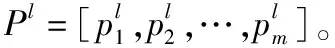
(4)

采用多个连续的子窗口异常波动率向量来表征纺纱过程波动状况,当滑动窗口中的监测数据波动稳定时,指标异常波动率也处于合理的波动范围,该子窗口的质量波动为正常波动。当纺纱过程滑动窗口中出现异常监测数据时,由于质量波动出现异常预期信号,其对应的指标异常波动率也出现剧烈变化,此时将包含异常监测数据的子窗口序列标记为异常波动模式。

因此,纺纱过程质量波动异常预警问题就可以转变为纺纱过程多质量参数子窗口模式识别问题,通过对纺纱过程进行子窗口序列分解,识别出现异常预期信号的子窗口时刻。根据其指标异常波动率向量与正常纺纱过程异常波动率向量间的差异,及时判别出现异常波动模式的窗口序列,识别预期异常信号并对异常原因进行追溯,完成纺纱质量波动异常预警。

2 质量波动异常预警建模

2.1 基于随机森林的窗口波动模式识别

基于以上分析,本文将纺纱过程质量波动异常预警建模问题转变为多质量参数子窗口模式识别问题。其实质是在纺织过程的正常波动模式与异常波动模式之间构造决策面,依据构造的决策面对质量波动的不同特征模式进行识别,然后对识别出的异常波动模式进行报警。随机森林能够处理非线性高维特征数据,且形成的决策树对非训练样本仍能表现较高的识别精度,鉴于此,本文采用随机森林对异常波动窗口模式进行识别。

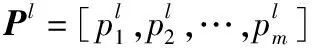
1) 选定适宜的随机森林参数,包括决策树个数ntree、最大特征数目m。通过bagging对{P1,P2,…,Pl,…,PN}进行有放回抽样,共抽取N个样本形成训练子集,未抽到的样本构成袋外数据L。

2) 从m个监测参数中随机选取c(c≪m)个特征参数,按照基尼系数进行节点分裂,分裂不进行剪枝。重复步骤1和步骤2,建立ntree棵决策树的随机森林。

3) 使用ntree棵决策树对L中的窗口波动类型进行预测,采用简单多数投票原则计算出最终的分类结果,并与实际运行状态的标签比对,得到L的分类误差R。

(5)

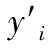
随机森林模型的最优参数选择通过最大化分类精度来获得,在基于随机森林算法做窗口模式分类时,在训练样本一定的情况下,影响分类精度与时间复杂度的主要因素有两个：生成一棵决策树所随机选取的属性特征数量(简称特征数量)c和最终生成的决策树数量ntree。因此以最大化分类精度为优化目标,采用四折交叉及网格化搜索法对(c,ntree)两种参数进行参数选择。

2.2 纺纱过程质量波动异常预警策略

纺纱过程质量波动异常预警模型由质量波动表征和质量波动异常识别两部分组成,构建如图2所示的质量波动异常预警策略,具体实施过程如下：

1) 给定纺纱过程中多维质量监测参数{xl1,xl2,…,xlm|l=1,2,…,n},对其归一化后构建窗口宽度为β、步长为1的滑动窗口,并进行子窗口划分,得到窗口状态矩阵W=[W1,W2,…,Wn-β+1]T。

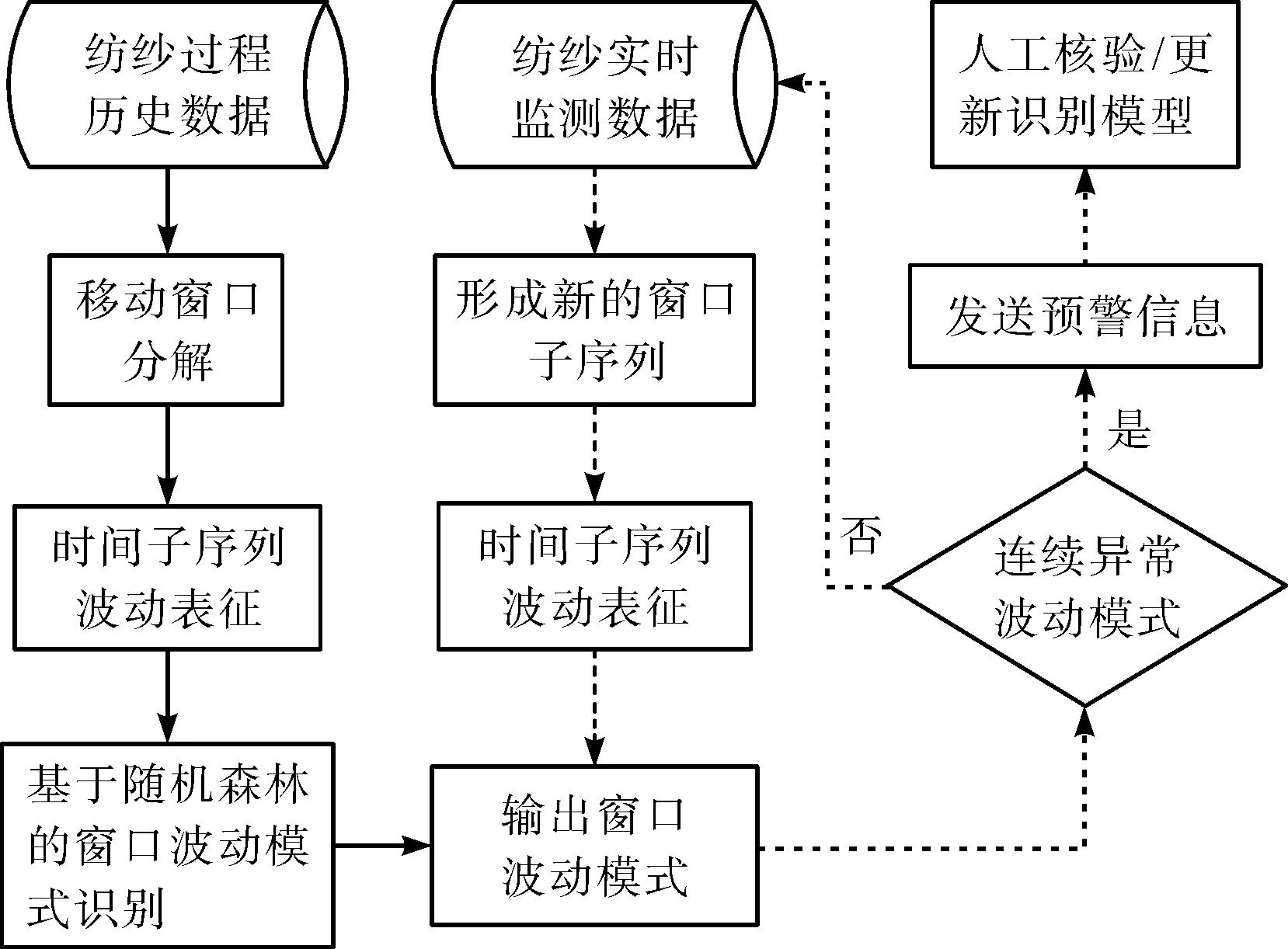
图2 纺纱过程质量波动异常预警策略Fig.2 Abnormal warning strategy of quality fluctuation during the spinning process

2) 基于波动表征原理,对各子窗口序列进行均方根误差的求取并完成[0,1]的异常概率映射后,得到纺纱过程的窗口序列P,并根据子窗口是否含有异常数据进行标记,得到对应的窗口波动模式Y=[y1,y2,…,yn-β+1]。

3) 以{P,Y}为随机森林的训练样本,对子序列波动模式进行随机森林建模,结合网格化搜索确定窗口波动模式识别模型的最优参数。

4) 对实时的监测数据进行新窗口序列的构建,并完成波动程度的表征后输入到随机森林的窗口波动模式识别模型中,输出具体的波动模式。

5) 以连续出现异常波动窗口为预警条件,对实时监测数据进行质量波动异常预警,降低偶然波动对预警精度的影响,确定警告发生时刻及异常原因。

6) 发送预警信息后,人工核验纺纱过程实时状态,并进行识别模型的更新。

3 实例分析

以纺纱过程的细纱工序为例,验证质量波动异常预警方法的有效性。细纱工序是纺纱生产过程中的最后一道工序,其过程稳定程度决定了纱线质量的好坏,主要涉及到10个质量影响参数,参考优化后的部分最优工艺条件[20],并根据实际细纱工序的关键影响参数进行正态分布的数据采样,参数分布如表1所示。其中细纱工序异常采用定点施加扰动产生,采样数据包含正常波动的细纱数据和施加扰动的异常细纱数据两种数据类型共计500组样本,异常细纱过程数据包括：第一段(351～400组)和第二段(451～500组),其中异常数据为对毛条含油施加均值为0.5、标准差为0.3的异常扰动数据及对纤维细度施加均值和标准差均为1的异常扰动数据。

表1 细纱工序的关键质量影响参数分布Tab.1 Key quality parameter distribution for the spinning process

3.1 纺纱过程质量波动表征

为分析纺纱过程质量波动表征的有效性,首先以301～316组的毛条含油数据为例进行滑动窗口分解与波动表征。通过对[1.1,1.2,1.2,1.3,1.1,1.2,1.2,1.1,1.4,1.2,1.1,1.3,1.2,1.1,1.3,1.1]进行窗口宽度为15、步长为1的子窗口划分,得到2个毛条含油窗口子序列：[1.1,1.2,1.2,1.3,1.1,1.2,1.2,1.1,1.4,1.2,1.1,1.3,1.2,1.1,1.3]和[1.2,1.2,1.3,1.1,1.2,1.2,1.1,1.4,1.2,1.1,1.3,1.2,1.1,1.3,1.1]。

(6)

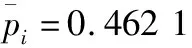
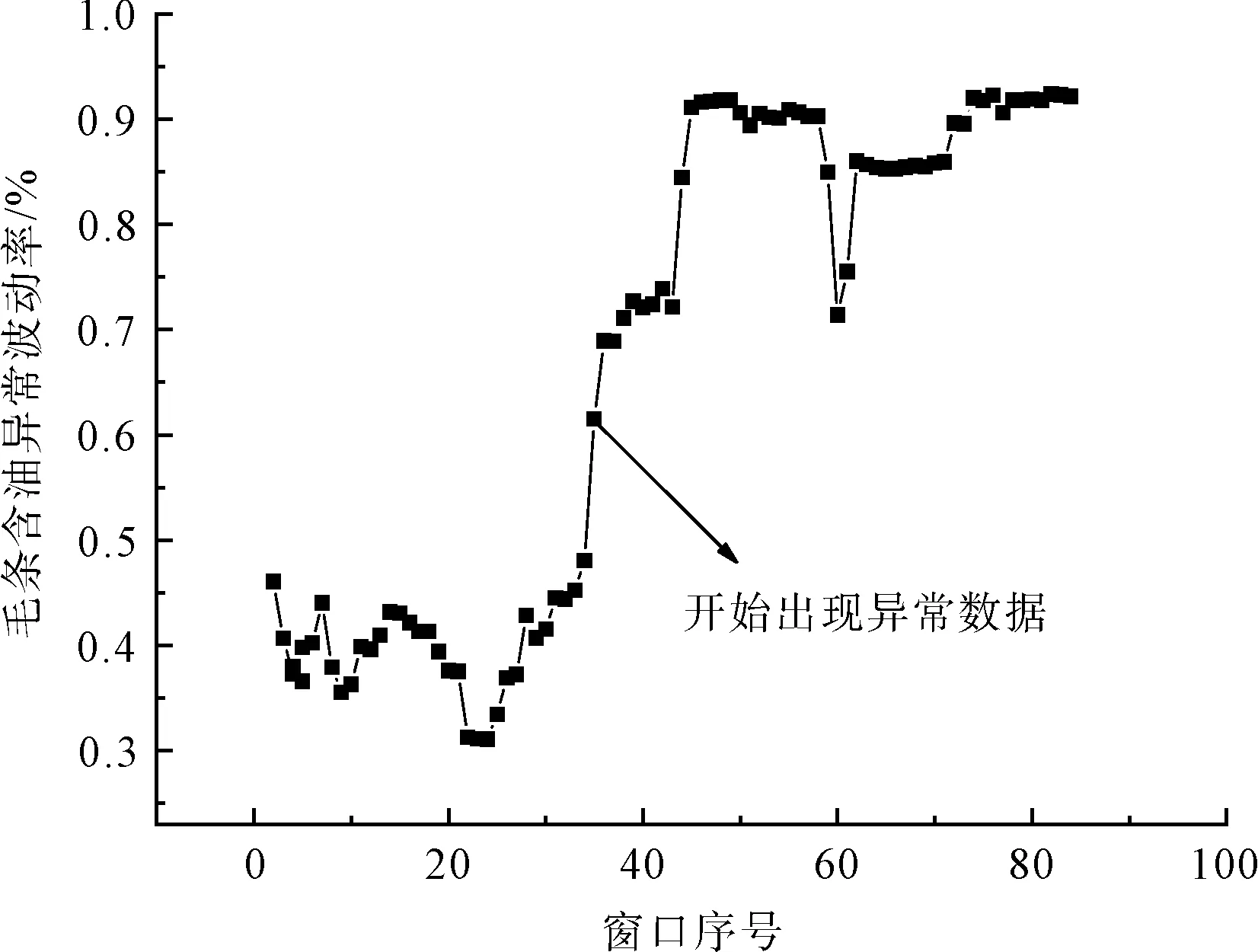
图3 毛条含油异常波动率变化Fig.3 Abnormal fluctuation rate change of wool top oil

3.2 不同窗口宽度对异常波动表征的影响

为分析不同窗口宽度对异常波动表征的影响,分别对301～400组的细纱数据10个指标进行纺纱过程质量波动表征。首先对该段细纱过程进行滑动窗口分解,分别选取滑动窗口的宽度为10、20、30,窗口每次移动一个时间点,对301～400组细纱数据集进行移动窗口分解;然后计算子窗口所有指标的异常波动率,每个子窗口的质量波动程度由10个指标的异常波动率表征。考虑到图片的可读性,仅对301～372组数据的毛条含油、毛条回潮、纤维细度及纤维离散指标异常波动率进行展示,其指标异常波动率的分布变化如图4所示。对比图4的(a)(b)(c)三个子图可以看出,不同的窗口宽度对波动表征效果具有一定的影响：窗口宽度过小容易导致其波动率的变化范围较大,其表征结果容易受到偶然波动的影响,导致对加工状态的误判;窗口宽度过大也会造成表征结果对异常数据不敏感。

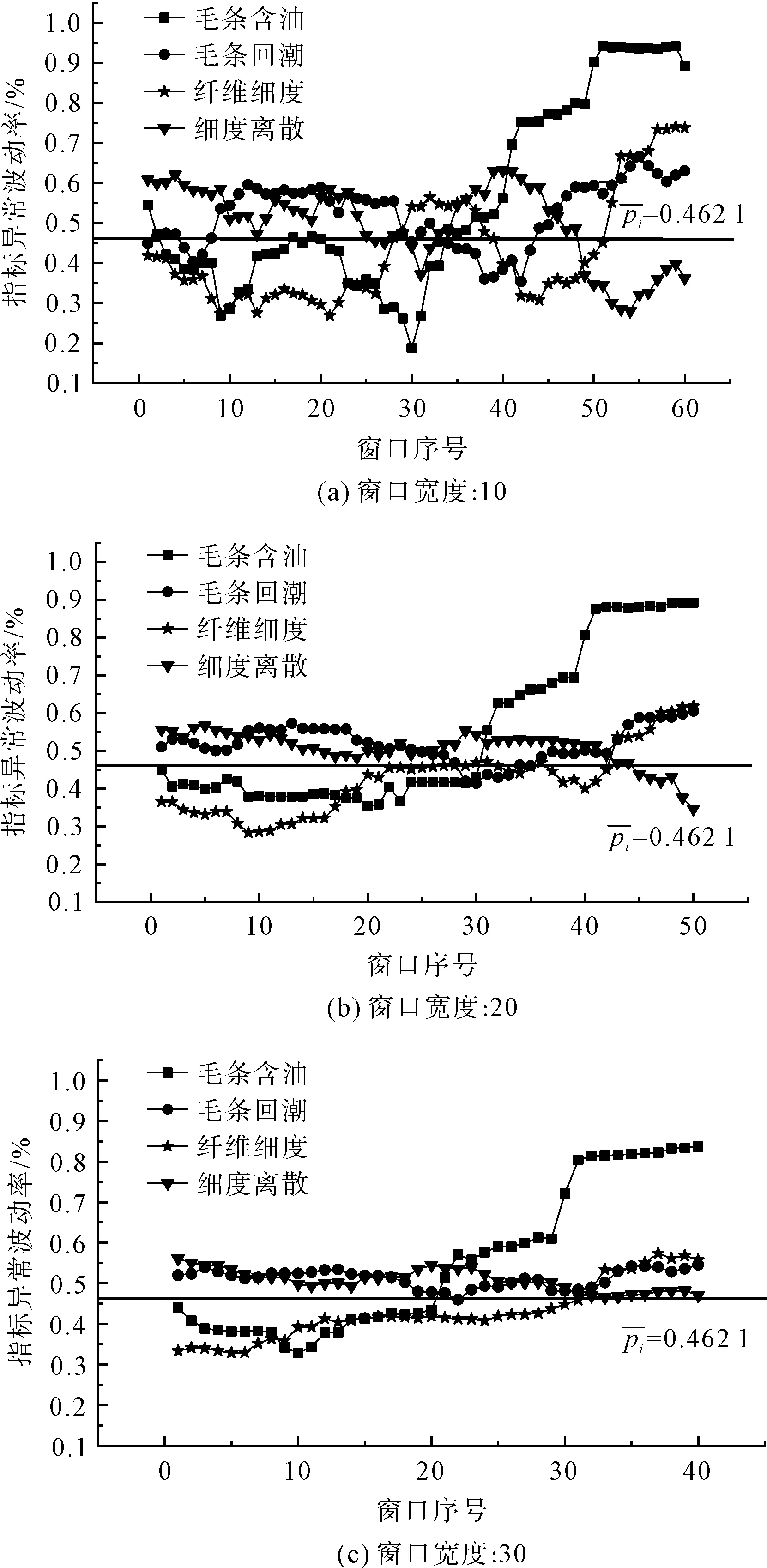
图4 细纱过程各指标异常波动率分布变化Fig.4 Abnormal fluctuation rate distribution change of each index in the spinning process

3.3 基于随机森林的纺纱波动预警建模

进行细纱过程质量波动异常预警模型构建时,首先提取1～400组样本数据建立随机森林子序列波动模式识别模型,并采用网格化搜索及交叉验证对随机森林模型进行c∈(2,10)、ntree∈(1,100)的参数优化。设置c、ntree的网格大小分别为1、10进行粗略搜寻,搜寻后锁定c∈(2,10)、ntree∈(35,45),然后设置网格大小均为1对该区间进行精确寻优,两次寻优过程如图5和图6所示,最后确定c=8、ntree=42为随机森林模型的最优参数。

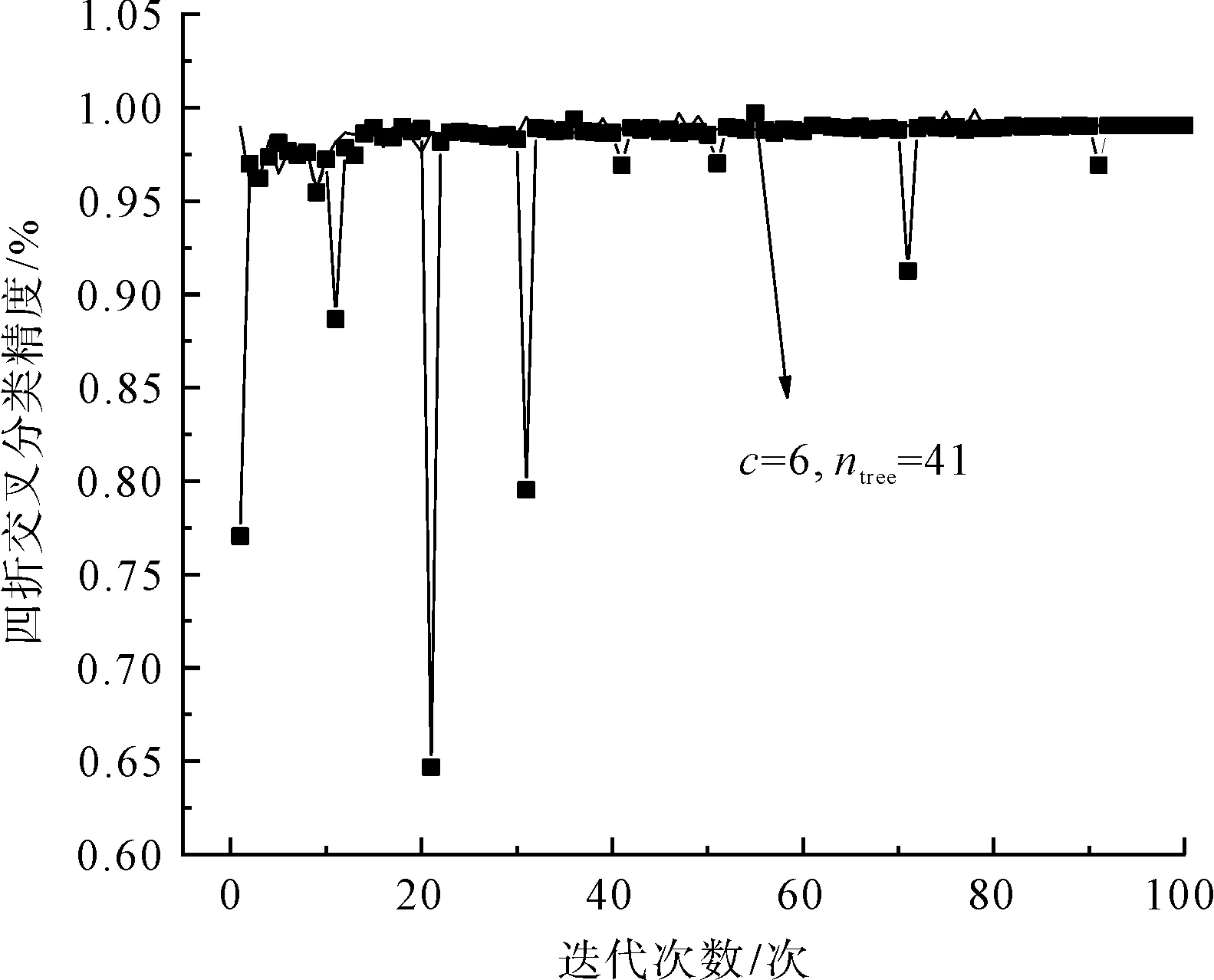
图5 网格大小为1、10的区间锁定Fig.5 Interval locking with grid size of 1 and 10

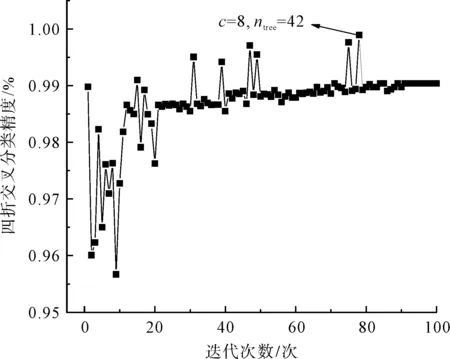
图6 网格大小均为1的精确寻优Fig.6 Accurate optimization with all grid sizes of 1

为选择合适的窗口宽度,基于构建的随机森林模型对不同窗口宽度构成的子窗口序列进行识别。图7显示了不同窗口的波动表征对识别精度的影响,可以看出,窗口宽度过小容易导致其波动率的变化范围较大,造成对子窗口的波动模式的误判而产生误警现象;而窗口宽度过大时对异常数据的感知能力较弱,影响了异常波动预警的及时性。因此,采用窗口宽度为15、步长为1构建纺纱质量波动表征模型。

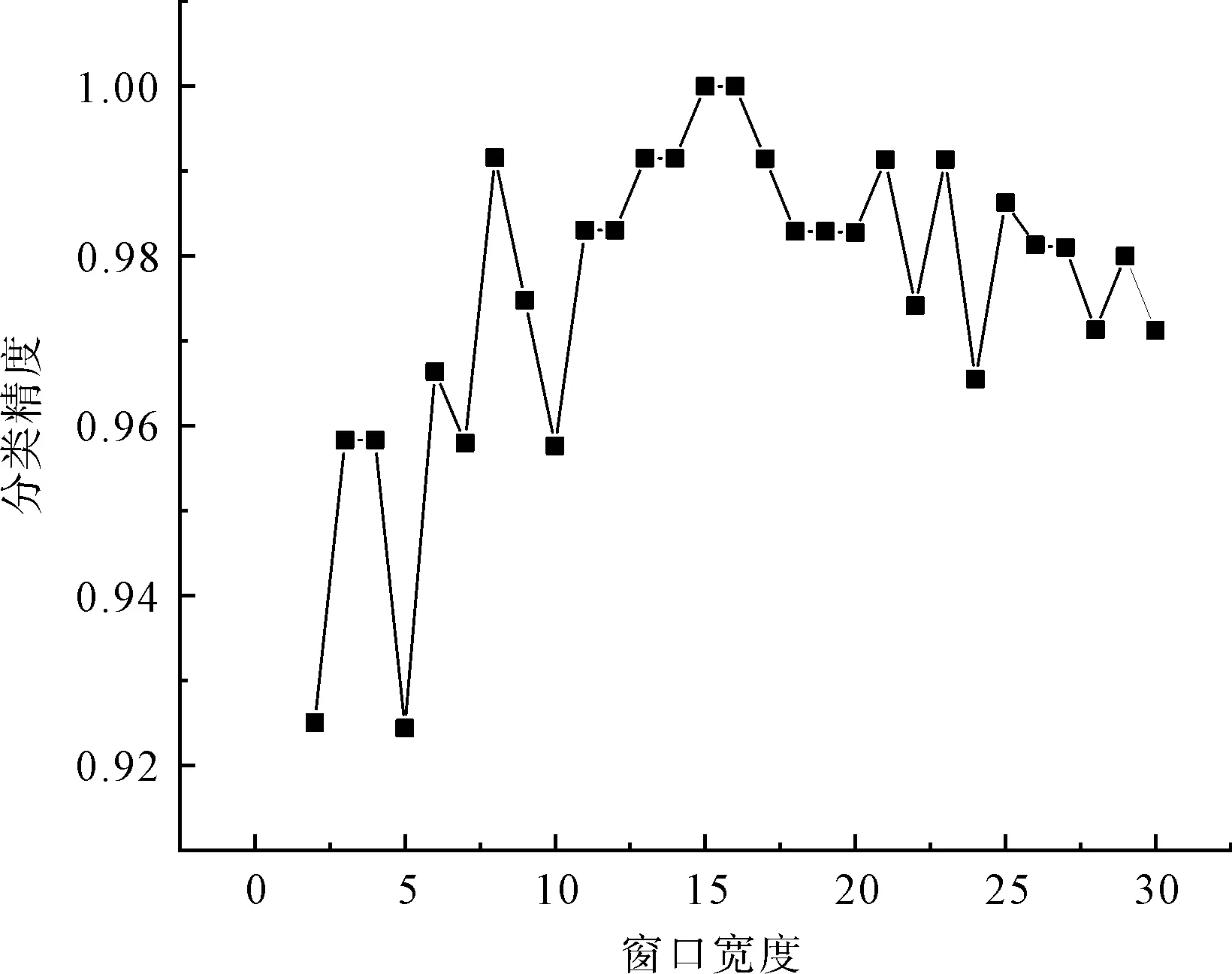
图7 不同窗口的波动表征对识别精度的影响Fig.7 Influence of different window widths on recognition accuracy

基于窗口宽度为15、步长为1的波动表征模型及优化随机森林模型对401～500组样本进行质量波动异常预警,以一个窗口为单位进行该段细纱过程的窗口子序列划分,形成86个窗口序列,并计算其指标异常波动率,依次对各子窗口进行模式识别,其波动模式输出结果和滑动窗口移动过程分别如图8和图9所示。由图8可以看出,实际窗口模式在第37个滑动窗口处发生波动模式的转变。结合图9的滑动窗口在样本序列中的移动过程可知,此时滑动窗口移动到第51组(异常信号出现)样本处;而提出的随机森林预警方法在异常信号出现后的第二个窗口识别出波动模式的转变,此时滑动窗口移动到第52组样本处,且此后一直维持异常波动模式,按照连续出现异常波动模式的预警策略,在第38个窗口发出预警信息,该模型的窗口波动模式识别率达到98.82%。

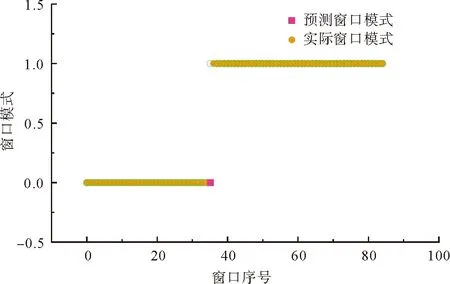
图8 质量波动模式输出结果Fig.8 Output result of the quality fluctuation mode

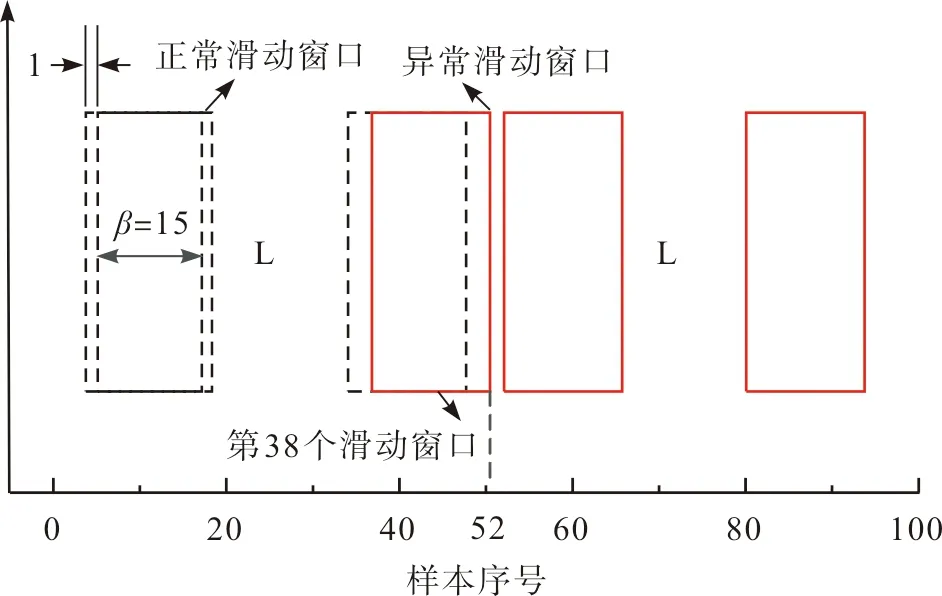
图9 滑动窗口模式识别图解Fig.9 Sliding window pattern recognition diagram

3.4 不同算法对纺纱质量波动预警效果的影响

为了分析构建的质量波动异常预警模型效果,采用窗口宽度为15、步长为1作为波动表征模型参数,分别选取支持向量机(Support Vector Machine,SVM)和K-最近邻算法(K-nearest neighbor, KNN)对401～500组数据进行窗口模式识别效果的对比分析。图10和图11显示了不同算法的纺纱质量波动模式识别结果,可以看出,基于SVM和KNN的纺纱过程质量波动模式识别在异常初期无法及时预警,且在后续模式识别中还会将异常窗口模式误判为正常窗口模式,导致漏警问题。

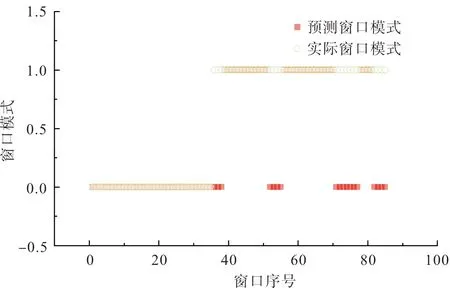
图10 基于SVM的纺纱质量波动模式识别Fig.10 Spinning quality fluctuation pattern recognition based on SVM

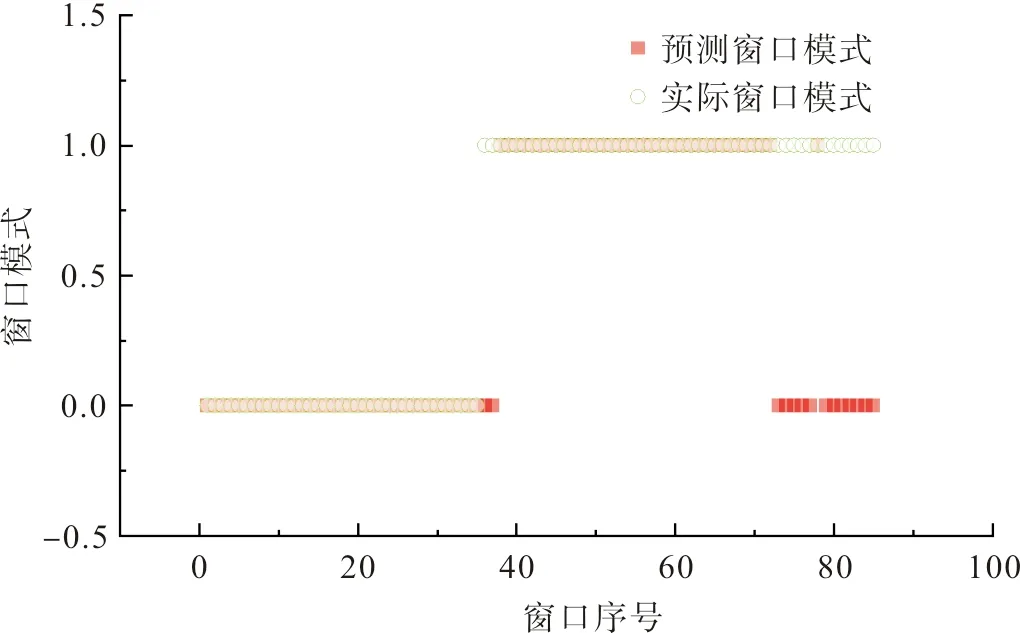
图11 基于KNN的纺纱质量波动模式识别Fig.11 Spinning quality fluctuation pattern recognition based on KNN

为进一步说明本文提出方法的有效性,表2统计了不同算法模型在波动模式识别过程中的效果对比。由表2可以看出,在波动模式识别准确率指标层面,基于SVM和KNN的纺纱过程质量波动模式识别方法要远低于基于随机森林的方法,较易造成漏警和虚警问题;在预警时刻及时性的指标层面,所提方法在出现异常信号后的第2个窗口(第38个子窗口)就给出预警信息,相比KNN和SVM算法均提前进行了报警,说明所提方法可以对纺纱过程异常波动进行提前预警;在建模时间上,本文提出的方法略高于其他几种算法,这是由于随机森林属于集成方法所致,但各方法建模时间均为毫秒级,并不会增加实际应用的建模难度。综上,本文所提方法在提高波动模式识别准确率和提前实现预警同时,不会增加实际应用难度,较其他方法具有一定的优异性。

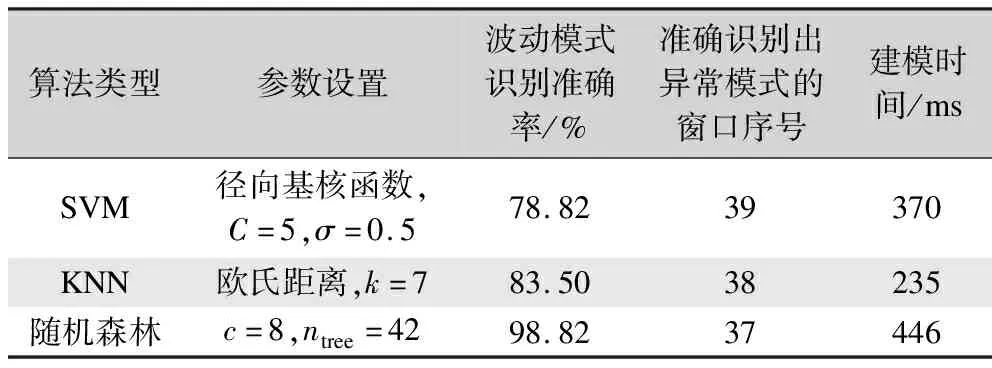
表2 不同算法的纺纱质量波动模式识别效果对比Tab.2 Comparison of spinning quality fluctuation pattern recognition effects for different algorithms

3.5 纺纱质量异常波动溯源分析

基于细纱过程质量波动异常预警结果,对其中的异常波动模式窗口进行异常溯源分析。对识别为异常窗口的48个窗口子序列的异常原因进行识别,识别结果如图12所示。由图12可以看出,前13个窗口子序列均为毛条含油异常,中间8个窗口为纤维细度异常,后续窗口为两种异常波动的复合异常。识别结果与实际异常类型相符合且识别精度达到100%,说明提出的方法能够在进行异常波动预警的同时,实现异常波动源头的精准判断,从而为生产人员提供了异常源信息,有效保证了纱线生产过程的持续稳定。

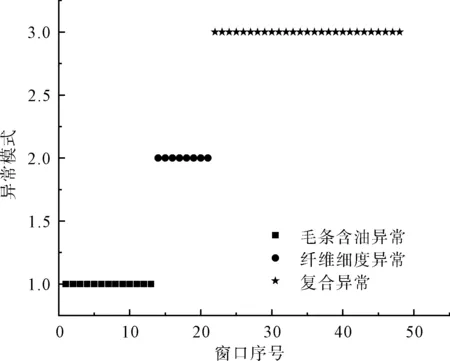
图12 纺纱质量异常波动溯源分析Fig.12 Traceability analysis of abnormal fluctuation of spinning quality

4 结 论

本文针对纺纱过程质量波动异常预警问题,提出了基于窗口波动模式识别的纺纱过程质量波动异常预警方法。以纺纱过程中的细纱加工为例进行验证,结果表明所提方法能够有效对细纱过程的异常质量波动进行及时准确的早期预警,并能实现异常信息的准确溯源,为保障整个纺纱生产过程的安全稳定提供理论依据。

《丝绸》官网下载

中国知网下载