混凝土-聚苯板复合墙板受力性能试验研究

赵考重李景录魏欣

(1.山东建筑大学土木工程学院，山东 济南 250101；2.山东建筑大学工程鉴定加固研究院有限公司，山东 济南 250013)

0 引言

随着建筑行业的快速发展，建筑的节能减排越来越受重视，提高能源的利用率是实现资源合理化的重要方式[1]。 研究发现，对于耗能较高的建筑，超过70%的建筑耗能是由于围护结构的热传递造成的[2-3]。 因此，在实际工程中广泛应用外墙外保温系统以减少围护结构的热传递、提高能源利用率[4-6]。 但受环境条件的影响，外墙外保温系统存在脱落风险，给城市运行带来安全隐患，地震时还会产生次生灾害[7-9]。 而混凝土-聚苯板复合墙板是具有集承重、保温、围护功能于一体的外墙自保温系统，克服了外墙外保温系统易产生脱落的缺点，对其力学性能的研究可为实际工程应用提供理论依据。

国内外对各种复合墙板开展了一系列研究。LIAN[10]对比了复合墙板与实心墙体的极限承载力，发现复合墙板的承载力计算不能完全遵循实心墙板的承载力计算公式。 ASAN[11]采用克兰克-尼科尔森(Crank-Nicolson)方案研究了保温层在复合墙板的最优位置。 蒋金梁[12]分析了复合墙板在整体结构中的力学行为，发现在框架结构中复合墙板内外叶面层可以很好地协同工作，并提出了复合墙板的承载力公式。 封雷等[13]开展了掺玻璃纤维网格布复合墙板的力学性能试验，表明相比于没掺纤维网格布的墙板，其承载力和抗弯能力有明显提升。 江焕芝[14]采用钢-纤维复合连接件夹芯复合墙板的抗弯试验，并模拟了风荷载对墙板的影响，表明连接件可以有效传递剪力，保证了墙板在使用过程中不易开裂。 孙倩倩[15]和黄良朋[16]研究了一种厚度为120 mm、混凝土面层为25 mm 的承重复合墙板，发现荷载作用下面层发生局部失稳破坏。 目前，已有的研究成果多是针对用于非承重的复合墙板，对于作为承重结构的复合墙板的研究，由于墙板所用材料、厚度、构造等不同，得到的结论也有差别。

基于上述研究，文章研制了一种主要应用于单层和多层建筑的承重复合墙板，并对这种复合墙板在竖向荷载作用下的受力性能开展了试验研究和数值模拟，得到了墙板轴心受压和偏心受压的破坏机理及承载力，为实际工程应用提供了理论依据。

1 材料与方法

1.1 试件材料及设计

研制的混凝土-聚苯板复合墙板由混凝土结构面层、聚苯板夹芯保温层、钢丝网架和连接件4 部分构成。 综合考虑保温、承重、防火和施工等各种因素，墙板设计厚度为200 mm、 聚苯板厚度为100 mm，两侧混凝土面层厚度均为50 mm，混凝土面层内配置钢丝直径为3 mm，网格尺寸为75 mm×75 mm 的钢丝网片；采用所研制的特殊连接件(如图1 所示)将两侧混凝土面层连成整体，该连接件可准确固定钢丝网位置，同时保证两侧混凝土面层共同受力。

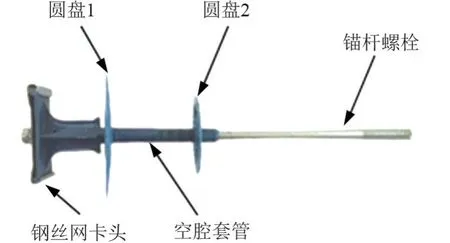
图1 墙板连接件图

1.2 试验设计

试验共设计了7 组14 个试件，包括4 组轴心受压试件和3 组偏心受压试件，每组两个试件，主要研究高厚比、偏心距对试件受力性能的影响。 钢丝网架由冷拔镀锌钢丝点焊制，钢丝直径为3 mm、钢丝网片混凝土保护层厚度为20 mm，混凝土设计强度等级为C30，实测混凝土标准立方体试件抗压强度为33.1 MPa。 连接件按间距375 mm×375 mm 布置，特制连接件可准确固定钢丝网的位置，同时将保温板两侧混凝土面层连接成整体。 保温板、钢丝网及连接件组装示意图，如图2、3 所示。

图2 钢丝网片组合构造示意图(单位:mm)

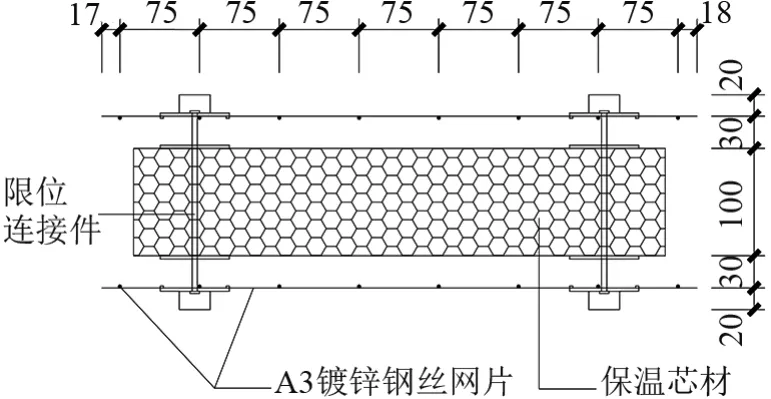
图3 双面钢丝网片组合构造(单位:mm)

7 组试件截面尺寸均为200 mm×600 mm，轴心受压试件高度H分别取1 500、2 000、2 500 和3 000 mm，偏心受压试件高度均为1 800 mm，偏心距分别取30、60、90 mm。 试件编号及设计参数见表1，其中编号以Z 开头的试件为轴心抗压试件，以P开头的试件为偏心受压试件。 试件示意图如图4所示。

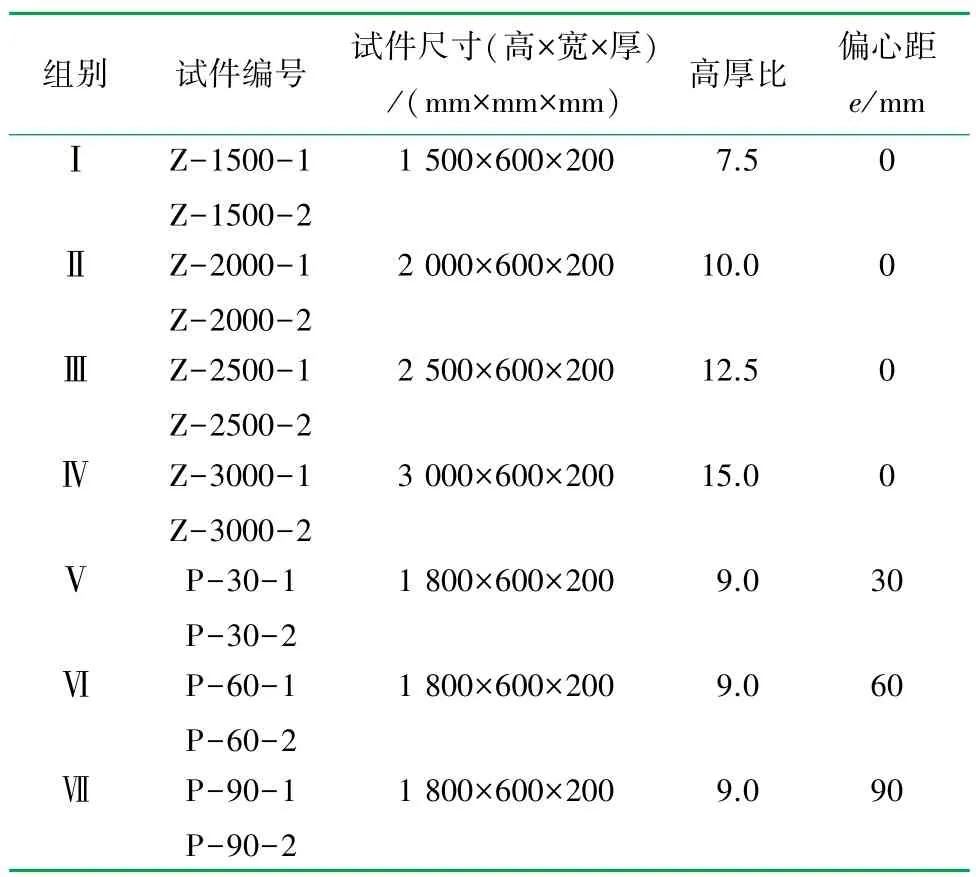
表1 不同试件尺寸及参数表

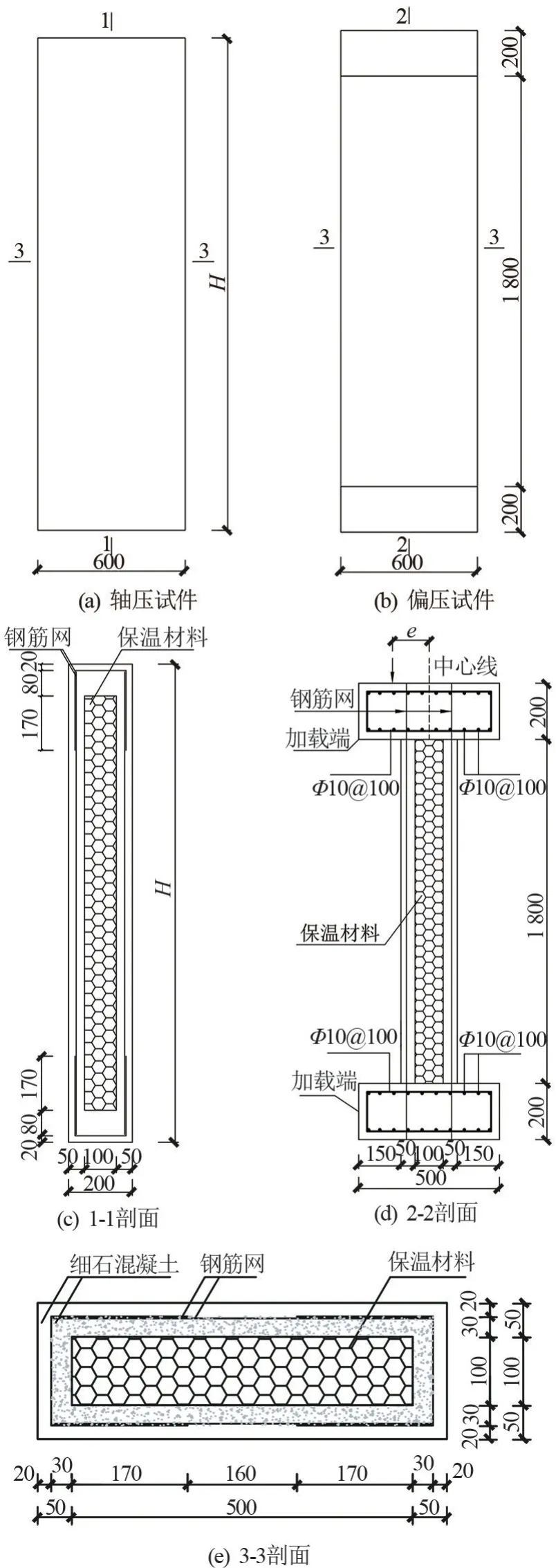
图4 试件示意图(单位:mm)

1.3 加载方式

试验在5 000 kN 压力试验机上进行，如图5 所示。 加载初期每级加载值取50 kN，当加载到接近破坏荷载时，每级加载值改为30 kN。

2 试验现象及结果分析

2.1 试验现象及特征分析

2.1.1 轴心受压试件

在轴心荷载作用下，8 块试验墙板的破坏过程基本相似，轴心受压试件裂缝发展如图6 所示。 在荷载作用下，试件的上、下端会产生竖向裂缝，随着荷载的增加，产生新的竖向裂缝并不断向上、下延伸，如图6(a)所示。 荷载加载到一定值，部分构件产生斜裂缝，并延伸形成U 形分布的裂缝，如图6(b)所示，说明墙板混凝土面层有外凸趋势。 试件最终破坏主要有两种情况:(1) 混凝土被压碎发生破坏，多发生在试件的下端，但也并非是整个截面，而是局部混凝土先被压碎，如试件下端的角部；(2) 个别试件的混凝土层外凸屈曲破坏，多发生在试件上端。 在极限承载力时所测墙板中部两侧混凝土压应变基本相同，且其值＜0.002，墙板平面外也基本没有变形。

轴心受压试件最终破坏形态如图7 所示。 试件端部首先产生竖向裂缝，原因是在竖向作用下，横向产生了拉应力。 另外，除个别试件有局部面层外凸趋势外，大部分试件都是由于混凝土被压碎而发生破坏，而且有外凸现象试件的承载力与其他试件也相差不大，说明所设置的墙板连接件在一定程度上能够保证混凝土面层的整体工作。 试件破坏时，混凝土面层局部由于被压碎引起破坏，因此截面上应力分布不均匀。 在承载力计算时应考虑应力不均匀对承载力的影响，并引入应力不均匀系数。

图7 轴心受压试件破坏形态图

2.1.2 偏心受压试件

在偏心荷载作用下，试件破坏面均在试件的端部，且为受压侧或压应力较大一侧面层混凝土被压发生破坏。 偏心距为30 mm 的试件，其端部墙板两侧均产生竖向裂缝；偏心距为60 mm 的试件，受压一层首先产生竖向裂缝，然后另一侧产生水平裂缝；偏心距为90 mm 的试件，先受拉侧产生贯通面层的水平裂缝，且其数量较多，然后受压侧会产生竖向裂缝。 试件最终破坏形态如图8 所示。 当偏心距较小时，试件全截面受压；当偏心距较大时，墙板一侧受压而另一侧受拉，因此墙板产生水平裂缝。 另外，试件均为混凝土被压碎发生破坏，未出现面层外凸失稳现象，说明连接件保证了偏心受压试件面层的整体工作。

图8 偏心受压试件破坏形态

2.2 试验承载力结果与分析

2.2.1 轴心受压试件

轴心受压试件的极限承载力试验结果见表2。第Ⅲ组两个试件承载力试验结果的离散性较低，这可能是由于试件加工时材料存在离散性。 除试件Z-2500-2外，其余试件的承载力试验结果相差不大，而且个别高厚比大的试件承载力还略大于高厚比小的试件，说明高厚比对试件的承载力影响不大。其原因是:(1) 连接件保证了混凝土面层和聚苯板的整体工作，作为整体的墙板试件的高厚比不大；(2) 由于墙板混凝土压应力分布不均匀，试件破坏时材料性能未得到充分发挥，破坏荷载小于截面混凝土所达到抗压强度的承载力，而达到极限承载力时墙板平面外基本无变形，因此破坏时墙板的整体稳定性对承载力影响并不显著。

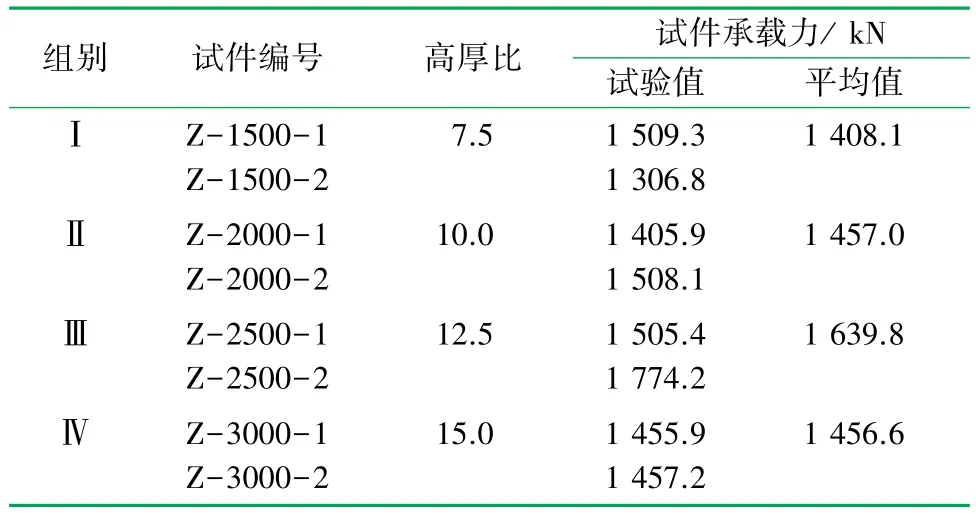
表2 轴心受压试件承载力试验结果表

由试件的破坏形态可知，试件截面上压应力分布不均匀，破坏时局部混凝土被压碎发生破坏，个别试件存在混凝土面层外凸现象，材料未得到充分发挥。 由承载力试验结果得到，试件的高厚比对承载力影响不大，可忽略高厚比的影响。 另外，由于配筋率较低，在承载力计算时可忽略钢丝对竖向承载力的影响。 因此，当高厚比≤15 时，墙板试件的轴心受压承载力由式(1)表示为

式中Nu0为复合墙板轴心受压承载力，N；β为承载力折减系数；fc为混凝土轴心抗压强度，由试验得到fc＝25.2 MPa；Ac为混凝土净截面面积，mm2。

根据式(1)得到试件的承载力折减系数β由式(2)表示为

将试件承载力试验值和fcAc的计算结果代入式(2)，得到各组试件的承载力折减系数，见表3。 除第Ⅲ组试件外，其余各组试件的承载力折减系数比较接近，取其他3 组试件的折减系数平均值作为墙板试件承载力折减系数，即β ＝(0.80＋0.83＋0.83)/3＝0.82，则墙板试件轴心受压构件承载力由式(3)表示为

表3 轴心受压试件承载力折减系数试验结果表

2.2.2 偏心受压试件

偏心受压试件的极限承载力试验结果见表4。由试验结果可知，在偏心荷载作用下，墙板的承载力将会降低，偏心距越大，承载力越低，因此偏心距对构件的承载力有明显的影响。 考虑偏心距影响，偏心受压构件的承载力由式(4)表示为

表4 偏心受压试件承载力试验结果表

式中Nu为偏心受压墙板承载力，N；α为偏心距对承载力影响系数。

将式(3)代入式(4)，得到高厚比≤15 的复合墙板的偏心受压构件承载力，由式(5)表示为

将表4 中试验结果代入式(5)，可得到Ⅴ、Ⅵ和Ⅶ各组试件的偏心距影响系数α的试验结果分别为0.92、0.81 和0.60。 根据α的试验结果，经回归分析得到试件的偏心距影响系数α，由式(6)表示为

式中h为复合墙板厚度，其值取200 mm。

各组试件受压承载力试验结果与公式计算结果对比见表5。 除第Ⅲ组轴心受压试件外，其余各组试件公式值与试验值的误差均＜5%，两者吻合较好。

表5 试件承载力试验与公式结果对比表

3 有限元分析

3.1 模型建立

3.1.1 模型简化

由于聚苯乙烯板的材料性能对复合墙板的承载力影响不大，因此不考虑EPS 板参与承担荷载，故将墙板中间的保温层视作中空。 为方便施加荷载以及模拟实际试验条件，在墙板两端设置垫块，为保证基座以及加载梁在试验过程中的刚度，将两端垫块截面简化为矩形，且其材料的弹性模量取值为钢材弹性模量的100 倍。

3.1.2 单元类型选取与网格划分

混凝土材料采用三维实体减缩积分单元(C3D8R)，钢筋采用三维线性桁架单元(T3D2)，其网格大小为50 mm。 墙板有限元模型如图9 所示，其中RP-1、RP-2 为节点。

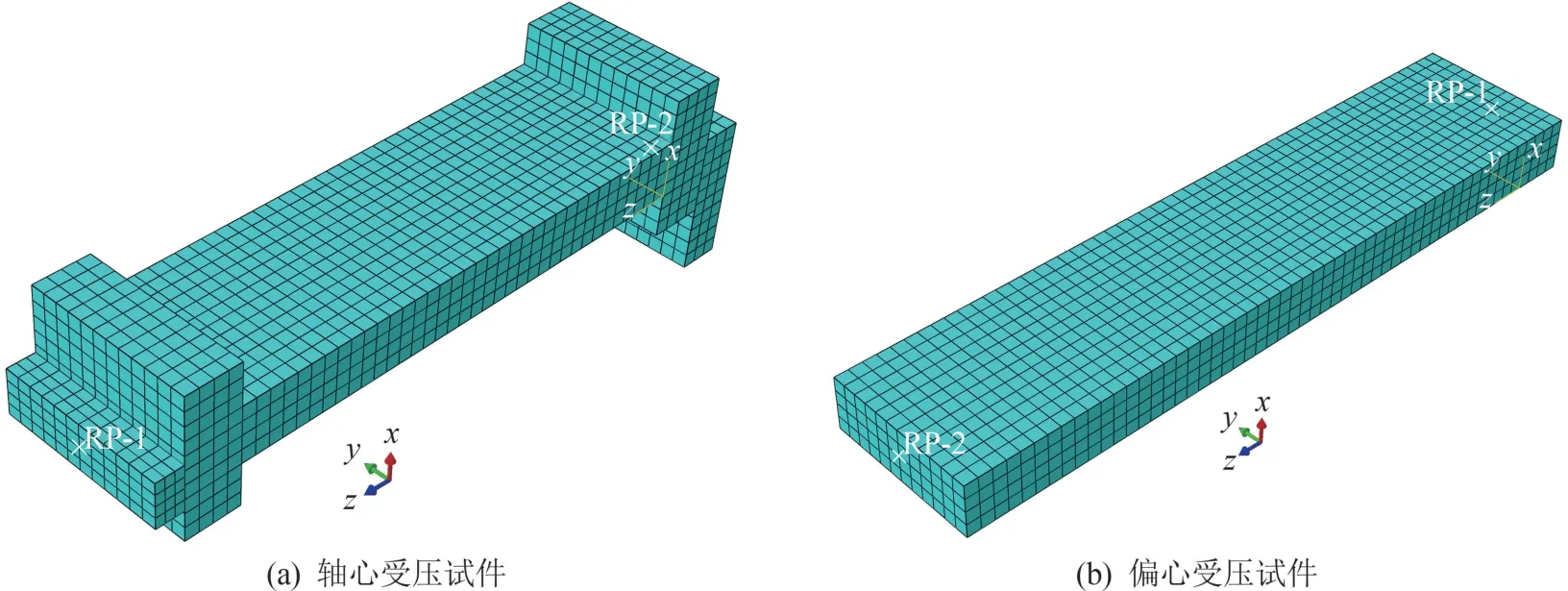
图9 墙板有限元模型示意图

3.1.3 接触类型

模型需要建立忽略混凝土与钢筋的相互作用，因此采用分离式方法完成试件的模型建立。 采用嵌入区域约束将钢筋内置于墙板混凝土区域内，采用绑定约束将加载垫块与墙板上、下端绑定。

3.1.4 边界条件及加载方式

墙板上部垫块加顶面约束耦合至RP-1，采用顶部固结(x、y、z方向的位移和转角均固定)；下部垫块底面约束耦合至RP-2，采用位移加载且x、y轴的转角未锁死(x、y、z方向的位移固定，绕z轴的回转固定)。

3.2 材料本构关系

在有限元软件ABAQUS 中，混凝土本构模型采用损伤塑性模型，根据GB 50010—2010《混凝土结构设计规范》[17]附录C.2 中的相关公式，计算得到混凝土应力-应变关系。 混凝土损伤塑性模型中定义的混凝土塑性损伤模型参数取值如下:膨胀角为30°、偏心率为0.1、双轴与单轴抗压强度之比fb0/fc0为1.16、不变量应力比K为0.666 7、黏性系数为0.005。

数值分析中钢材采用理想弹塑性模型。 当钢材屈服后，在不增加荷载的基础上，变形可自由增加，应力-应变关系曲线如图10 所示。

图10 钢材理想弹塑性模型应力-应变关系曲线图

图10中，σ为应力、ε为应变、fy为钢材屈服强度，而εy、εu分别为屈服应变和极限应变。 低碳钢丝弹性模量取2×105MPa，fy的试验值为531 MPa、泊松比为0.3。

3.3 结果分析

3.3.1 应力分析

轴心受压试件与偏心受压试件的应力云图分别如图11、12 所示。 试件的应力分布不均匀，不同高度轴心受压试件的上、下端局部应力较大，不同偏心距受压试件较大应力发生在受压一侧的上、下端部，与不同高度轴心受压试件应力分布类似。 模拟结果较好地验证了试验中该墙板的破坏出现在两端，且局部受压先发生破坏现象，混凝土材料性能未得到完全发挥。

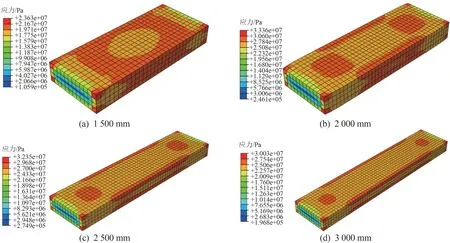
图11 不同高度轴心受压墙板应力云图

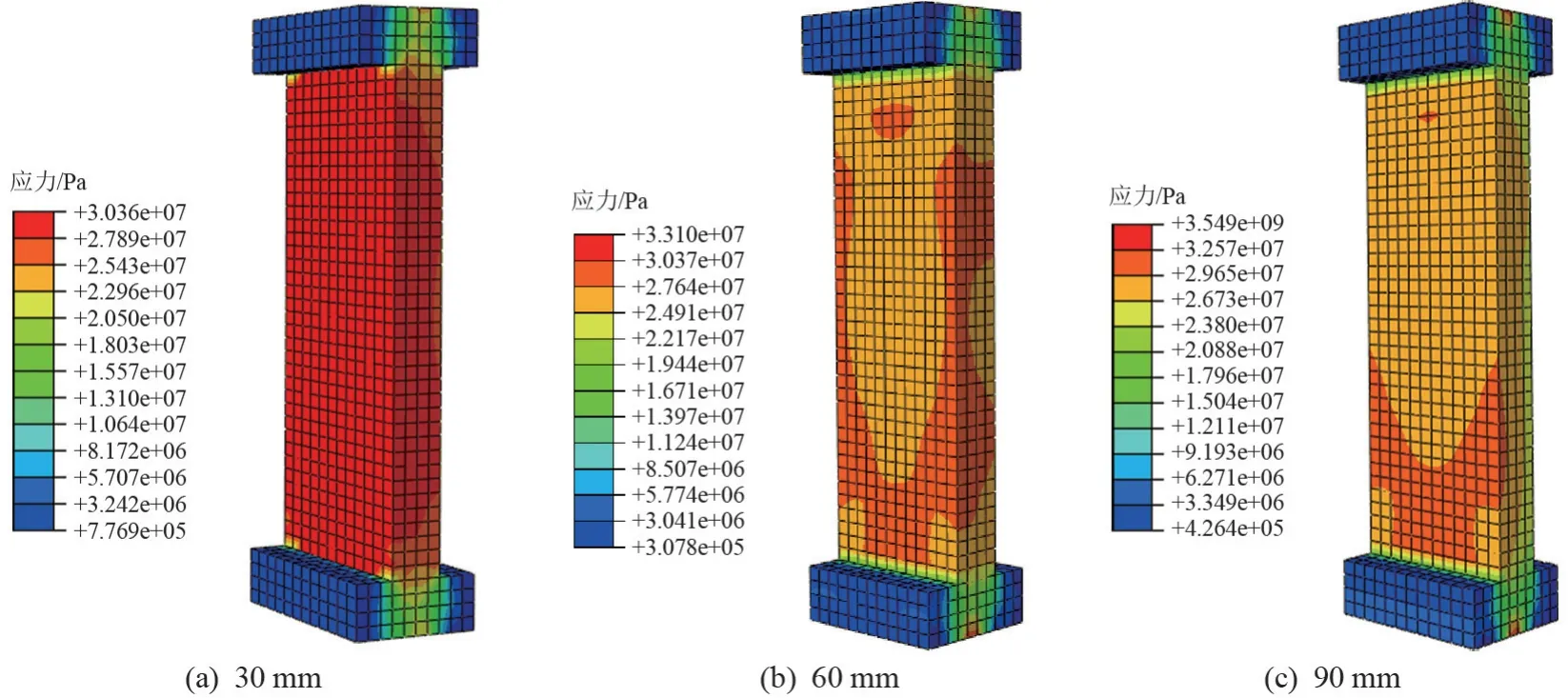
图12 不同偏心距受压墙板应力云图

3.3.2 墙板承载力分析

模拟分析得到的各试件极限承载力见表6。 复合墙板极限承载力模拟值高于试验值，这是由于数值模拟考虑的都是试件的理想状态，但误差均＜10%，说明模拟结果与试验结果吻合较好。

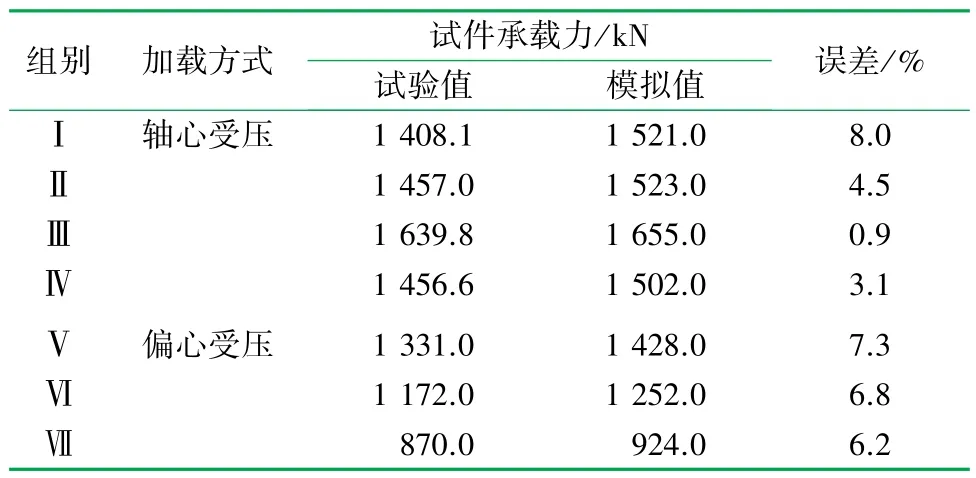
表6 试件承载力试验与模拟结果对比表

4 结论

通过对研制的混凝土-聚苯板复合墙板进行不同高厚比的轴心受压和不同偏心距的偏心受压试验研究，给出了复合墙板的承载力计算公式，并得到以下主要结论:

(1) 研制的混凝土-聚苯板复合墙板采用的连接件及布置方式可准确固定钢丝网位置，同时可保证混凝土面层、聚苯板整体工作，但在竖向荷载作用下，截面应力分布不均匀，材料性能未得到充分发挥。

(2) 在荷载作用下，试件最终面层混凝土被压碎发生破坏，个别试件有混凝土面层外凸趋势，破坏截面位于试件的上、下端。 在竖向荷载作用下，面层混凝土压应力分布不均匀，计算承载力时应考虑0.82的不均匀系数。

(3) 当高厚比≤15 时，对混凝土-聚苯板复合墙板的受力性能影响较小；在偏心荷载作用下，偏心距越大，墙板承载力越低，显然偏心距对墙板承载力有显著影响。 试件承载力公式计算值与有限元模拟值、试验结果均比较吻合。