掘进机器人电液系统位置控制死区补偿
张国泰, 沈 刚, 汤 裕, 李 翔
(中国矿业大学 机电工程学院, 江苏 徐州 221116)
引言
煤矿巷道掘进正朝着自主定型定向的趋势发展,煤炭的高效开采对掘进装备的自动化水平提出了新的要求[1-2]。电液驱动系统作为掘进机截割系统的重要组成部分,具有典型的强非线性、多源扰动以及参数不确定性等特征,严重影响着电液控制系统的性能。比例换向阀是电液比例控制系统中的核心控制元件,其通常存在5%~20%不等的位移死区, 对掘进机截割电液驱动系统而言, 这类死区将对巷道断面的轮廓成形产生不利影响,液压执行器换向滞后容易造成断面边帮发生超挖或欠挖等工艺难题,因此就电比例阀死区对掘进机截割电液系统的位置控制影响展开了研究。
死区作为机电系统中一种典型的非线性环节,国内外众多学者已对死区特性展开了大量研究。某大学的Taware教授等[3-4]较早地研究了死区自适应补偿方法,但是算法结构复杂,使其难于在工程中推广应用;Coelho LD等[5]针对电比例换向阀存在的时变死区特性,设计了反馈线性化控制器和死区参数自适应律并进行了仿真研究;文献[6]针对含不确定性死区的阀控对称缸伺服系统设计了基于backstepping的自适应鲁棒控制器,通过仿真验证了死区自适应补偿算法的有效性;文献[7]针对含有未知输入死区的非线性系统,通过构造死区逆模型并结合反演递推技术,提出一种自适应鲁棒输出反馈控制器,通过仿真实例验证了控制方法的可行性;彭熙伟等[8]针对电液比例系统的变死区特性,采用模糊逻辑在线调节比例阀的死区补偿量,一定程度上降低了系统跟踪误差;刘延俊等[9]利用神经网络算法在线调整比例阀控制电压,以缩短比例阀在死区附近停留时间来降低其对系统控制性能的影响;苏琦等[10]为解决大流量先导式换向阀换向滞后问题,针对先导级的中位死区提出一种解耦变增益补偿算法,其中死区逆的补偿增益可以随先导阀芯位移、主阀控制腔压力在线调整;刘白雁等[11]针对电液比例系统中比例阀死区引起跟踪波形削顶问题,提出一种超前切换+变幅值的在线死区补偿方法;王立新等[12]针对比例阀死区采用了光滑死区逆补偿方法,并将死区补偿误差引入自抗扰控制器,从而改善了阀控缸系统的位置/力跟踪精度;孟凡淦等[13]针对气动伺服系统中比例阀死区采用直接逆模型进行补偿,结合非线性鲁棒控制器提高了气缸的轨迹跟踪精度;与上述直接叠加电压阶跃信号不同,张佳旭等[14]提出比例阀阀芯过死区时对其位置参考信号叠加一个衰减式位置补偿量以缩短阀芯跨越死区的时间。
纵观现有研究成果,目前电液比例控制系统中针对比例阀死区的补偿方法主要分为固定参数逆补偿和自适应补偿两种方法。一方面,描述死区特性的参数与油液黏度、阀芯阀体间隙等有关,死区时变特性将对传统定参逆补偿效果产生不确定性影响;另外,由于比例阀频宽较低,不能简单地视为比例环节,定参逆补偿方法仍需结合系统位置控制器来提高性能。针对非线性不确定性系统,自适应控制是一种常规的控制方法,能够有效地处理系统参数的时变摄动,但现有死区自适应控制的研究多局限于理论分析与仿真模拟,或一些智能控制算法计算量较大,参数收敛慢,不利于实际应用。
综上所述,为提高掘进机器人截割电液系统的位置控制精度,设计了死区自适应补偿控制器,利用搭建的掘进机试验台将所提控制方法与传统的死区补偿技术进行了对比实验,验证了所提方法的有效性。
1 比例阀死区描述
电比例换向阀的结构死区可表征为阀芯位移xf与阀口开度xio或阀芯位移xf与阀口流量Qv的非线性关系,并且受机械制造和安装精度影响,比例阀的结构死区通常具有轻微的不对称性,如图1所示,阀口遮盖量bra≠bla,brb≠blb。除结构死区外,比例阀的驱动电路、电磁铁磁滞、阀芯静摩擦力以及弹簧预紧力等也会产生电气控制死区,可表征为放大器输入电压ur与阀芯位移xf的关系。由于本研究比例阀采用了位移外环、电流内环的双闭环PID控制,故可不考虑阀的电气控制死区。

图1 电比例换向阀结构死区Fig.1 Dead-zone of EPDV
2 电液比例系统模型
2.1 比例阀建模
阀芯运动过程中将受到黏滞摩擦力、稳/瞬态液动力和非线性电磁力等,很难建立比例阀的精确数学模型,先通过遗传算法离线辨识得到了阀的传递函数,然后在该模型基础上进行动态性能优化,其中,比例阀的传递函数模型为:
(1)
用阀芯实际位移uf与死区电压阈值ud描述阀的中位结构死区,并假设阀不存在过渡位死区,即在图1中bra=brb=br,bla=blb=bl,设udr和udl为阀的正、反向死区电压阈值,udr和udl均大于0,阀的死区特性可描述为:
uio=Kxuxio=uf-sat(uf)
(2)
式中,Kxu—— 阀芯位移传感器转换增益
xio—— 阀口开度
sat函数表达式为:
(3)
2.2 阀控缸系统建模
掘进机截割电液驱动系统是一种典型的阀控非对称缸系统,系统工作原理如图2所示。
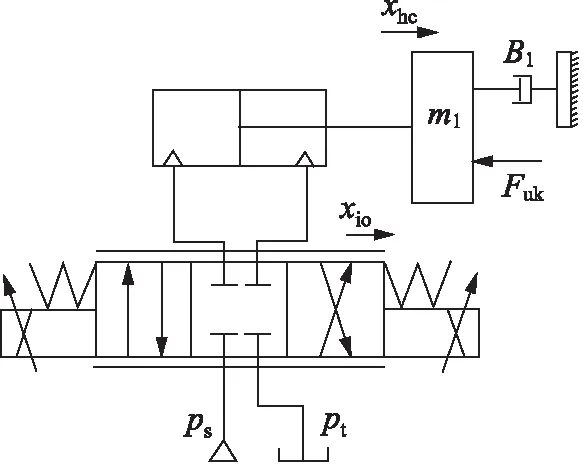
图2 阀控非对称缸系统Fig.2 Diagram of electro-hydraulic position control system
比例阀流量方程为:
(4)
式中,ps—— 泵源供油压力
pt—— 系统回油压力
p1—— 液压缸无杆腔压力
p2—— 液压缸有杆腔压力
uf≥0时,s(uf)=1;uf<0时,s(uf)=0。
不考虑油液泄漏,液压缸流量连续性方程为:


(5)
式中,q1,q2—— 无、有杆腔流进或流出的流量
A1,A2—— 无、有杆腔活塞作用面积
V11,V21—— 无、有杆腔容积
V10,V20—— 无、有杆腔初始容积
βe—— 液压油有效体积弹性模量
xhc—— 活塞位移
液压缸力平衡方程为:
(6)
式中,m1—— 活塞杆运动组件质量
B1—— 油液黏性阻尼系数
Fuk—— 其余未建模负载力
定义A2/A1=η,pL=p1-ηp2,根据式(4)和式(5)得到:
(7)
从而
(8)

sgn(·) —— 符号函数
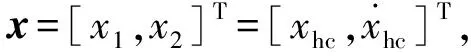
(9)
3 位置控制器设计
3.1 系统控制器
定义比例阀死区参数D=[udr,udl]T,并对系统控制量进行补偿
(10)
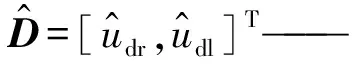
uin—— 进入死区前的控制量,
μ=[μ1,μ1-1]T,uin≥0时,μ1=1;uin<0时,μ1=0
根据式(2)得到比例阀的实际开口量
(11)
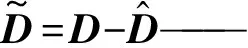
δ—— 死区模型与实际模型的偏差,且有‖δ‖≤1
(12)
式中,
定义误差变量y=z2-φ(z1),其中辅助变量φ(z1)=-lnsigα(z1),sigα(z1)=|z1|αsgn(z1),ln>0,α>0,则式(12)转换为:
(13)
(14)
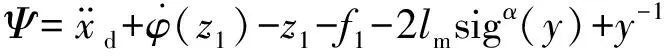

(15)
式中,ε—— 任意小的正数
3.2 参数自适应
为便于系统稳定性分析,先介绍如下引理[15]。
引理1 对于非线性系统
如果存在一个原点的邻域U∈Rn上的函数V(x)是正则和C1光滑的,且同时存在实数1>λ>0和c>

(16)
定理1 针对掘进机器人截割系统(9),设计死区

(17)

则:
=-z1lnsigα(z1)-ylmsigα(y)-
(18)
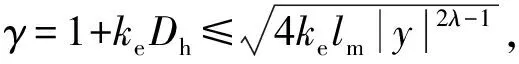
(19)
式中,η=min{2λln,2λlm}
由引理1可知,设计的死区自适应律可以保证系统有限时间内稳定。
3.3 非线性项处理
控制律(14)中含有不确定控制增益g1,本研究将g1视为标称值gn,并将由此产生的偏差和f1看作新的非线性项f2,则系统状态方程可写成:
(20)
将gn和f2代入式(14)得到:
(21)
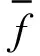
(22)
4 实验验证
4.1 掘进机器人实验平台
为验证所提控制算法有效性,利用搭建的悬臂式掘进机器人样机(如图3所示)对截割系统的俯仰摆角控制进行死区补偿实验。试验台上位机控制系统主要基于xPC/Target快速原型技术开发,利用MATLAB/Simulink软件编写控制程序,设计完成后使用VC++进行编译,编译通过后直接下载至工控机中,上位机和下位机之间通过TCP/IP协议进行通讯。研华PCI-6208输出板卡提供±10 V控制电压,再经功率放大器压流转换后给比例换向阀提供最大1.5 A线圈电流,比例阀位移传感器反馈信号可以从功率放大器上的I/O口测量获取,通过电压转电压型信号隔离器实时传送阀芯位移信号。研华PCI-1716板卡采集油缸位移信号和两腔油压信号。华德DBEE10型电比例溢流阀可以设定泵出口压力在0~20 MPa范围内,A7V40型斜轴式电比例变量泵按设定排量22 mL/r运转。

图3 掘进机器人Fig.3 Roadheader test rig
根据系统元器件的样本参数及现场测试,给定系统模型的标称参数及控制器设计参数分别如表1和表2所示。

表1 系统模型参数Tab.1 Main parameters of system model

表2 控制器参数Tab.2 Controller parameters
4.2 实验结果与分析
为了验证控制算法的有效性,首先针对掘进机截割头俯仰油缸的伸缩位置分别采用传统的闭环P控制、闭环PI控制、光滑死区逆补偿+P控制、光滑死区逆补偿+PI控制与提出的自适应死区补偿方法进行对比实验。其中P(PI)控制器的比例系数为kp=0.1,积分系数为ki=0.25, 光滑死区逆模型的表达式为:
(23)
对俯仰油缸的运动轨迹利用五次多项式进行规划,设定油缸外伸位移为200 mm,过程最大运动速度为16.7 mm/s,最大加速度为2.778 mm/s2。首先对比传统的4类死区补偿控制器的轨迹跟踪效果,实验结果如图4所示。由图4a和图4b可以看出,单纯采用P控制会产生较大的动态跟踪误差和稳态定位误差;在给定合适的死区补偿参数后,采用光滑死区逆补偿+P控制可以有效减小跟踪过程的误差,且稳态阶段定位误差可以更快地收敛于0;PI控制由于I的积分作用,动态跟踪误差相较上述两种方法减小,但I引起的超调使得稳态阶段的定位误差是渐进收敛于0。在PI控制基础上结合光滑死区逆补偿可以进一步降低动态跟踪过程的误差,并且在稳态阶段定位误差的收敛时间得到缩短。由图4c可以看出,尽管采用了光滑死区逆补偿,在系统稳态定位阶段,比例阀阀芯颤振程度相较不加补偿有所加剧,这将影响比例阀的使用寿命,降低系统的可靠性。

图4 传统死区补偿方法实验结果Fig.4 Experimental results of traditional dead-zone compensation methods
进一步地,采用本研究提出的死区自适应补偿控制器与光滑死区逆+P控制器、光滑死区逆+PI控制器的实验对比结果如图5所示。
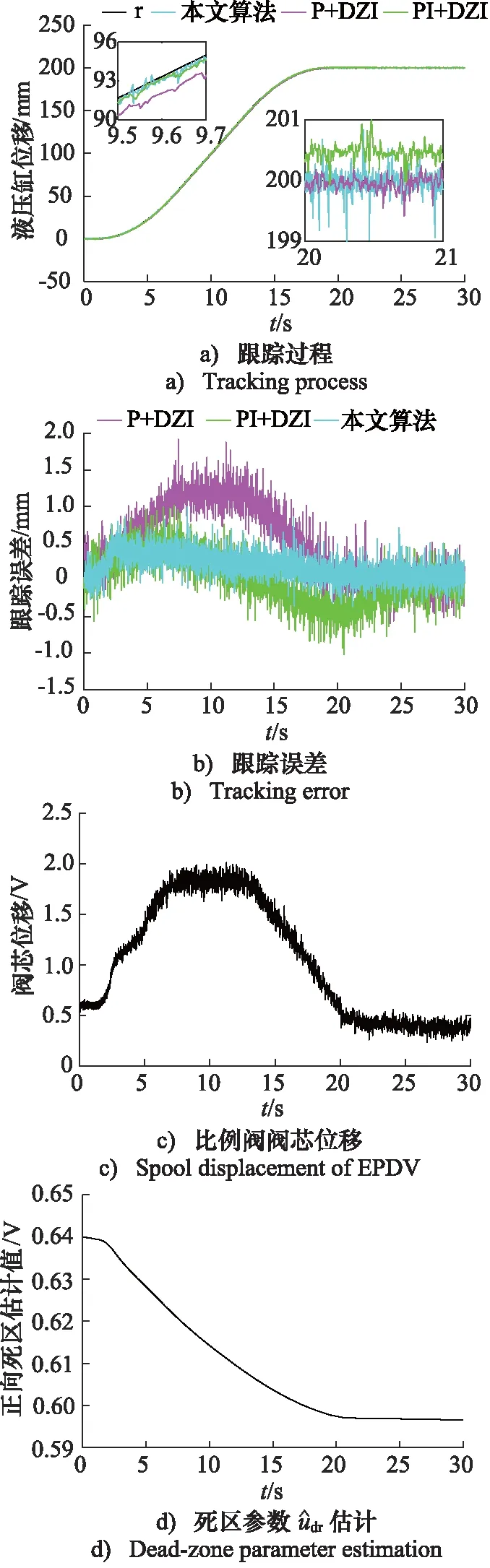
图5 死区补偿实验结果Fig.5 Experimental results of dead-zone compensation method in this paper
从图5a和图5b可以看出,控制器在有限时间内实现了对阀控缸系统参考轨迹的稳定跟踪,且在动态跟踪阶段相较传统的光滑死区逆补偿+P控制算法具有更小的跟踪偏差,相较光滑死区逆补偿+PI控制方法具有更小的稳态定位偏差,从而有效地抑制了比例阀死区对系统跟踪与定位性能的影响, 进而提高掘进机截割电液系统性能。另外,从图5c可以看出,采用的死区参数自适应算法还可以改善系统稳态时的比例阀阀芯颤振现象,进一步保证了比例阀持续工作的可靠性。
5 结论
针对掘进机器人截割系统中电比例换向阀结构死区影响截割头位置控制问题,设计了一种死区自适应补偿控制器,主要得到了以下结论:
(1) 建立了电液比例位置控制系统的阀控非对称缸模型,基于李雅普诺夫稳定性理论设计了死区参数自适应律,最终实现了跟踪误差的有限时间收敛。
(2) 将控制器与传统的P(PI)+光滑死区逆的死区补偿方法进行实验对比,实验结果表明此方法可以有效地提高系统的控制性能,保证煤矿巷道断面的成形质量。

