多路阀K形节流槽阀口流阻特性
张宇航, 杨明昆, 艾 超, 余 聪, 闫桂山, 姜文光
(1.燕山大学 机械工程学院, 河北 秦皇岛 066004; 2.中山大学 智能工程学院, 广东 深圳 518107)
引言
多路换向阀(以下简称多路阀)是由两个及以上的换向阀作为主体的组合式换向阀,具有结构紧凑、流量特性好、不易泄漏等特点,广泛应用于工程机械液压控制系统[1]、起重运输机械[2]和其他要求操纵多个执行元件的行走机械[3]。但由于多路阀阀体及阀芯结构复杂且集成度较高,存在高压大流量工况下压力损失严重[4]、气蚀[5]、振动噪声[6]等不良现象,严重影响多路阀的工作性能。
为满足现阶段我国高端液压元件技术突破的紧迫需求,助力工程机械的电动化、智能化转型升级,对多路阀可靠性的基础研究具有重要意义。
多路阀阀芯上均布有多组结构尺寸各异的节流槽,通过调整阀体与阀芯的相对开度实现流量控制功能。目前对节流槽滑阀的研究主要集中在其内部流场特性、阻力特性、流致现象及结构优化等方面。YE Yi等[7]对球形、三角形和渐扩U形三种类型的滑阀节流槽的静态特性进行了数值模拟研究,分析了它们在流量特性、稳态液动力、节流刚度等静态特性上的差异,为节流槽滑阀特性研究提供理论支撑。LU Liang等[8-9]采用实验和数值模拟相结合的方法,对U形、V形节流槽滑阀内的旋涡空化形态特征进行了综合研究,并对空化耦合的阻塞流进行了建模和分析。王安麟等[10]提出了多路阀阀芯拓扑形态设计的流量数数学模型,建立阀芯节流槽结构参数与流量和压降的映射关系,基于遗传算法对阀芯拓扑形态进行优化设计,兼顾流量控制特性的同时有效降低了压降。在以往的研究中,一般采用传统的压降或局部阻力系数来评价流动阻力,但只能宏观地评价总阻力,而不能评价流场内各位置的阻力分布情况。
在对流传热领域中,往往通过场协同角来确定流场中的高、低阻区的分布。为了强化传热,GUO Zengyuan等[11]提出了对流传热的温度场和流场之间的协同关系。场协同原理已通过各种实验和模拟得到证实[12-13]。目前,场协同原理被广泛用于强化传热领域,但较少用于降低流体阻力。LIU Wei等[14]基于热能、机械能、组分质量和流体动量守恒的协同方程,揭示了速度、压力、温度和组分浓度之间的多场协同关系。YIN Yifei等[15-16]利用速度场与压力梯度场协同原理分析了弯管的减阻机理,并通过一系列导叶优化过程,得到了一种新型低阻弯头。吴施熠徽等[17]利用Fluent对两种不同型号的轴流式止回阀内流场进行数值模拟和流动场协同分析,并给出了减阻优化的设计思路。白云飞等[18-19]基于速度场与速度梯度场协同原理研究了V、U形节流槽滑阀流场内的流阻和机械能耗散情况,分析了流体流向、节流槽结构参数等对场协同角的影响规律,但是只分析了x方向上速度场与速度梯度的场协同角分布情况,且未考虑速度场与压力梯度的场协同关系。
综上所述,诸多专家学者采用实验、CFD流场仿真技术等方法对节流槽滑阀内部流场进行可视化研究,探究了滑阀结构特征、边界条件等参数对阀内流量特性、流场分布、阻力特性及空化、振动噪声等流致现象的影响规律。但是对滑阀节流槽的研究主要集中在U形节流槽,对K形节流槽滑阀阀口的流场分布情况及阻力特性研究较少。
将CFD流体仿真技术和湍流场协同理论应用于装载机多路阀铲斗滑阀联节流槽阀口的流场研究中。采用仿真软件Fluent对多路阀阀口处的流场进行稳态仿真,研究K形节流槽阀口面积特性;阀口开度和入口体积流量对K形节流槽阀口流场的速度、压力、涡流、压降场协同角等流场分布及阻力特性的影响规律。
1 物理和数学模型
1.1 多路阀铲斗滑阀联工作原理
以某型装载机多路阀铲斗滑阀联为研究对象, 如图1所示为多路阀铲斗滑阀联液压控制系统示意图,元件1为铲斗滑阀,通过操纵先导手柄调节先导压力a、b,驱动阀芯左右运动,控制铲斗油缸的伸出、中位以及收回动作,从而实现流量调节及换向功能;元件2为单向阀,主要用于防止因负载脉动造成的油液倒流,从而避免铲斗出现“点头”现象;元件3为主安全阀,对主油路进行超压保护;元件4和5为过载阀,对铲斗油缸7的A、B两腔进行过载保护;元件6为补油单向阀,在铲斗卸料时起补油功能,从而防止超越工况下液压缸油腔吸空。
如图2所示为铲斗滑阀工作原理示意图。铲斗滑阀为三位六通滑阀,包含有铲斗的卸料、中位及收斗三个位置。具体工作原理如下所述:当铲斗滑阀阀芯两端没有先导压力时,铲斗滑阀阀芯处于中位,油液从P口流入T口,铲斗油缸保持不动;当操纵手柄控制铲斗卸料时,铲斗滑阀阀芯在先导压力的作用下向左移动,形成P→B和A→T的流量回路,铲斗油缸缩回;当操纵手柄控制铲斗收斗时,铲斗滑阀阀芯在先导压力的作用下向右移动,形成P→A和B→T的流量回路,铲斗油缸伸出。
P→A或P→B回路为油液流出全周开口阀芯状态,A→T或B→T回路为油液流入节流槽状态,油液流动状态复杂。由于A→T和B→T回路油液流经的节流槽结构相似,本研究只着重分析B→T回路的阀芯节流槽结构及节流槽阀口的流场分布及流阻特性。
1.2 K形节流槽结构
图3为多路阀铲斗滑阀原型。阀芯台肩上均布有多组结构尺寸各异的K形节流槽。K形节流槽是由矩形铣刀沿着半径为Rn的圆弧轨迹切割阀芯台肩而成,其截面形状为矩形。K形节流槽阀口开闭过程中具有良好的阀口过流面积梯度和流量控制特性,有效提高了执行机构的操控性、微动性和响应性。因此K形节流槽滑阀广泛应用于对精度和稳定性要求较高的液压阀中。
1.3 数学模型
1) K形节流槽阀口面积
冀宏等[20]提出用最小过流面计算渐扩形节流槽阀口面积的确定原则。将K形节流槽阀口面积Ak按阀口开度处的截面积A1在斜面上的投影面积计算,如图4a所示,从而推导出K形节流槽阀口面积的计算公式如式(1)所示:

图4 K形节流槽阀口面积计算简图Fig.4 Calculation diagram of flow area of K-shape notch
Ak=A1·cosβ
(1)
但是当节流槽深度Dn较大,如图4b所示,K形节流槽范围覆盖到阀颈处,此时若按常规方法计算阀口面积误差较大。因此在常规K形节流槽阀口面积基础上加以改进,具体公式推导如下:
(2)
(3)
x01=x-x02
(4)
Ak=k·W
(5)
K形节流槽阀口面积可以表示为:
Ak=f(x,Rn,W,Dn)
(6)
式中,x—— 阀芯位移
x01—— 阀口开度
x02—— 封油长度
W—— 节流槽加工刀具宽度
Dn—— 节流槽深度
2) 场协同模型
场协同原理常用于对流换热的研究中,通过调整流场来减小速度矢量与温度梯度之间的夹角,从而强化传热。当流体流经节流槽时,由于流动方向和过流面积的改变,在节流槽口处会形成压力梯度和速度变化。引入场协同原理,比较速度矢量与压力梯度的协同角,分析流体流过节流槽阀口的局部阻力损失。协同角方程推导如下:
对于无体积力的稳态流体流动过程,动量方程如式(7)所示[21]:
ρU·▽U=-▽p+μ▽2U
(7)
将式(7)的两边乘以速度矢量U,得到流体的功率等于流体的动能损失和黏性功率消耗之和:
U·(-▽p)=(ρU·▽U-μ▽2U)·U
(8)
将方程(8)的两边取模,其中|U||-▽p|表示流体消耗的泵的输出功率,若流体消耗的泵功率低,则表明流体的动能损耗小,并且表明流体的黏性耗散功小:
|U||-▽p|=|ρU·▽U-μ▽2U||U|
(9)
从方程(8),可以获得压力梯度和速度矢量之间的协同关系,流体流动阻力受流速和压力梯度及它们之间的协同程度影响,θ反映了速度矢量和压力梯度之间的协同角:
评析: 光合作用被称为地球上最伟大的化学反应,人们对它的认识经历了漫长的过程。其中,绿色植物在光下能够产生氧气,是在课堂教学中通过金鱼藻实验就可以形成的小概念。因此通过以上经典实验,可以引导学生理解证据的作用,强调规范地获取证据、综合分析数据,就可获得A、 B、 C答案所表述的客观规律。通过试题,检测学生的素养和教学的效果。
U·(-▽p)=|U||-▽p|cosθ
(10)
(11)
式中, ▽p—— 压力梯度
▽U—— 速度梯度
U—— 阀内流体流速,m/s
ρ—— 阀内流体密度,kg/m3
μ—— 阀内流体动力黏度,N·s/m2
θ—— 压力梯度和速度矢量之间的协同角,°
由式(8)~式(11)可知,在U·(-▽p)一定的条件下,随着协同角θ的减小,压力梯度的做功能力增强,压降减小,流体的动能损失与黏性力耗散的功之和减小。因此,减小协同角θ意味着减小流动损失,即减小阀内流动阻力。
如图5所示为K形节流槽滑阀阀口处的压力分布和协同角θ示意图。蓝线代表负压梯度,红线代表流线。当流体进入滑阀时,流体将沿轴向平稳流动,压力梯度沿轴向分布。流体流经节流槽阀口时,由于阀口面积急剧收缩,压力梯度变化较大。且流动方向突然改变,在离心力的作用下,流体倾向于向外壁流动,加强了流体与内壁的分离,使压力梯度沿径向分布。此时,负压梯度与速度矢量所形成的夹角,即协同角θ。

图5 负压力梯度与速度矢量协同角Fig.5 Negative pressure gradient and velocity vector synergy angle
使用Fluent 2021 R1中的用户自定义场函数编写协同角θ。式(11)可以编写如下:
(12)
为了方便分析,保证协同角θ在0~90°范围内,将式(12)改写如下:
(13)
2 K形节流槽阀口面积特性分析
多路阀铲斗滑阀联回油流道B→T阀芯凸肩上分布有四个结构相同的K形节流槽。根据最小过流面计算阀口面积的原则,阀口面积由K形节流槽过流截面、全周端面、环状过流截面共同决定。阀口面积AK计算公式如下:
AK=min{Ak,Akmax+Aq,Ah}
(14)
Aq=2πRs(x-x02-x03)
(15)
(16)
式中,AK—— 阀口面积
Ak—— K形槽过流截面面积
Akmax—— 最大K形槽过流截面面积
Aq—— 全周开口面积
Ah—— 环状截面面积
x02—— 封油长度
x03—— 节流槽长度
Rs—— 阀芯凸肩半径
Rg—— 阀芯阀颈半径
本研究所参考的铲斗滑阀阀芯K形节流槽的主要结构参数为:Rs=14 mm;Rg=8 mm;Rn=10 mm;Dn=9.5 mm;W=8 mm;x02=4 mm;x03=6 mm,结合式(2)~式(6)及式(14)~式(16),得到阀口面积随阀芯位移变化的示意图如图6所示,阀口面积变化曲线如图7所示。
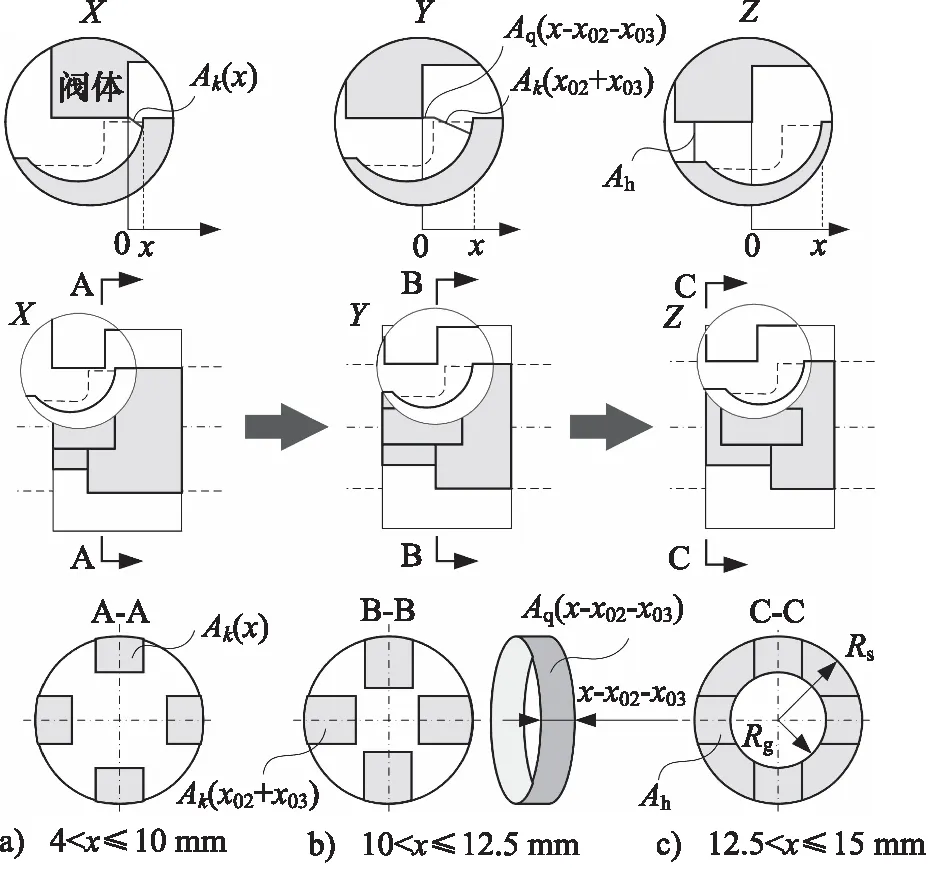
图6 阀口面积变化Fig.6 Change of valve port flow area
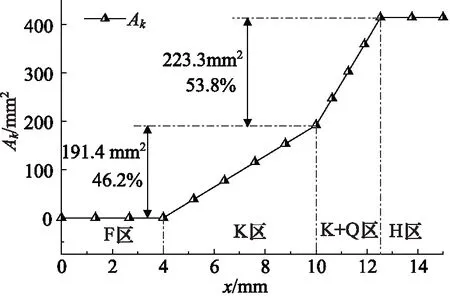
图7 阀芯位移与阀口面积关系Fig.7 Relationship between spool displacement and flow area
随着阀芯位移的增加,各阶段的阀口面积计算方法如下:
(1) 阀芯位移0≤x≤4 mm时,K形节流槽阀口未开,处于封油区(以下称“F区”),阀口面积AK为0;
(2) 阀芯位移4 AK=4Ak(x) (17) (3) 阀芯位移10 AK=4Ak(10)+Aq(x)=28π(x-10)+191.4 (18) (4) 阀芯位移12.5 针对高压湍流在多路阀内的复杂流动,采用Fluent软件进行数值模拟。为了提高仿真计算效率,基于ANSYS Workbench仿真平台,采用Fluent参数化仿真方法对多路阀铲斗滑阀联的流场进行数值模拟,参数化仿真流程如图8所示。 图8 Fluent参数化仿真流程Fig.8 Fluent parametric simulation process 1) 仿真参数设置 使用基于压力的求解器,为降低计算难度与计算资源消耗,采用雷诺时均法简化控制方程。并引入Realizablek-ε模型对时均化引入的雷诺应力项进行补充。基于压力的求解算法分为两类。一类是分离求解算法,包括SIMPLE、PISO等,分离求解算法主要应用于微压流动;另一类是耦合求解算法,如Coupled耦合算法,耦合求解算法主要应用于高速非压流动。通常,耦合求解算法在速度和压力值计算方面计算得更加精确。因此选择Coupled耦合算法作为求解算法。详细的仿真参数如表1所示。 表1 仿真参数Tab.1 Simulation parameters 2) 网格划分与独立性验证 将多路阀三维模型导入ANSYS Spaceclaim前处理软件中进行简化处理,并抽取铲斗滑阀联B→T回油流道并分割流体域。由于阀口处速度和压力梯度变化大,为了更好地模拟小开度时油液的流动状态,在阀口处设置BOI(Body of Influence),进而在网格划分模块中进行加密处理。 采用Fluent专用网格划分软件Fluent Meshing对流道模型划分非结构网格以更好地适应边界,并对阀口区域的网格进行局部加密以提高计算精度。体网格划分方法选择Poly-hex-core,对主流体域划分六面体网格,边界层划分棱柱层网格,过渡区域划分多面体网格。滑阀流体域网格划分情况如图9所示。 图9 滑阀流体域中心截面网格Fig. 9 Mesh of center section of spool fluid domain 为了避免网格数量对仿真结果的影响,在相同的仿真参数设置下,调整相应的面网格和体网格尺寸进行网格独立性分析。选取阀口开度为2 mm时的流体域作为验证算例,设定入口质量流率为3.625 kg/s,出口压力为0.1 MPa,计算的参考量为进出口压差。由表2网格独立性分析可知,当网格划分数量为83.7万时,继续增加网格数量,计算结果不再有明显变化,认为网格满足独立性要求。最终确定网格数量为83.7万,以保证网格的质量和计算资源的最佳配置。此时面网格最大Skewness值为0.40,体网格最小Orthogonal Quality值为0.33,网格质量良好。 表2 网格独立性分析Tab.2 Grid independence analysis 为了验证数值模拟的准确性,搭建装载机多路阀铲斗滑阀联静态性能测试试验台。多路阀测试试验台如图10所示。试验台主要由上位控制系统、数据采集系统及液压动力系统组成。以铲斗收斗时滑阀B→T油路为试验对象,通过控制面板设定入口体积流量为250, 350, 450 L/min,压力和位移传感器采集不同阀口开度下的进出口压差和阀芯位移。具体试验参数设置如表3所示。 表3 试验参数Tab.3 Test parameters 1.温度计 2、17.过滤器 3.定量泵 4.电机 5、15、16.流量计 6.蓄能器 7.安全阀 8、12、13、19、20.单向阀 9、10、11、14、18、21、22.换向阀 23、24、25、28.压力传感器 26.节流阀 27.位移传感器 29.控制面板图10 多路阀静态性能测试试验台Fig.10 Static performance test bench of loader multi-way valve 不同入口体积流量下压降特性试验数据及仿真数据对比如图11所示,可以看出不同入口体积流量下试验及仿真得到的压降特性具有相同的变化趋势,且仿真与试验值的误差低于15%,因此认为仿真结果能够真实反映实际工作时的节流效应。 图11 仿真试验对比Fig.11 Comparison between simulation and test 如图12所示为不同阀芯位移下进出口压差,随着入口体积流量的增加,进出口压差逐渐变大,且节流槽阀口的进出口压差随着开度的增加以对数函数趋势降低。进出口压差变化主要集中在“K区”, 此时阀口面积由K形节流槽阀口过流截面决定,阀口面积较小,压差较大,并随着阀芯位移的增加而迅速减小;当阀芯位移达到10~12.5 mm,此时处于“K+Q区”,阀口面积较大,进出口压差缓慢减小;当阀芯位移继续增加到12.5 mm,此时处于“H区”, 阀口面积为定值, 压差趋于稳定。 图12 不同阀芯位移下进出口压差仿真值Fig.12 Simulation value of pressure drop under different spool displacement 为了比较不同阀口开度、不同入口体积流量的K形节流槽滑阀优化前后的流场分布及阻力特性,分析了滑阀阀口处的压力、速度及场协同角分布。在相同的阀口开度下,流场呈现出相似的分布特征,因此结合第2节K形节流槽阀口面积特性分析,选择阀口开度为4、7和11 mm的滑阀对称面的流场,以分别反映低、中、大开口的流场分布状态。 1) 速度分析 如图13所示为不同入口体积流量、不同阀芯位移下阀口的速度分布云图及流线图。由速度分布云图可以发现节流槽处流体流动复杂,速度变化梯度较大。当高压流体通过阀芯从入口流进时,流体流速逐渐增大,且在节流槽处出现高速区。这是由于阀口过流面积的急剧减小,而入口体积流量不变,从而速度急速增大。这种速度冲击会对阀芯产生很大的冲刷作用,特别是当流体中含有一些杂质时,会加剧阀芯磨损。因此,降低阀芯处的最大流速及高速区范围对提高滑阀的性能具有重要意义。 图13 速度分布云图及流线图Fig.13 Velocity distribution counters and streamline 由速度分布流线图可以发现流体从进口流入,经过阀口时,流动方向由纵向变为横向,由于滑阀结构的限制和油液黏性力的影响,在阀芯凹角和K形节流槽中部形成涡流。高速附壁射流流出阀口,冲击阀腔顶部,只有靠近出口管道的流体会直接流出,其他流体都会聚集在阀体的顶部,产生大面积涡流,能量损耗严重。 对比不同阀口开度下的速度分布:随着阀口开度的逐渐增大,速度梯度逐渐减小,节流槽内流体最大流速逐渐降低,高流速分布区域从节流槽处逐渐向阀颈处移动;阀腔顶部的涡流尺度随阀芯位移增加而逐渐减小,节流槽处的涡核位置由节流槽中部逐渐过渡到阀芯凹角处。 对比不同入口体积流量下的速度分布:随着入口体积流量的增大,节流槽内流体最大流速、速度梯度随之增大,但是入口体积流量对节流槽内高速区、涡核区的位置及射流角的影响较小。 2) 压力分析 如图14所示为不同入口体积流量、不同阀芯位移下阀口的压力分布云图。由图14可以观察到,当高压流体通过K形节流槽阀芯从入口流进时,压力从入口到出口逐渐降低,且压降主要集中在K形节流槽等效阀口面积处,压力梯度在小开口时(x=4 mm)变化显著。同时阀口附近靠近壁面处形成了局部低压,此处容易产生气蚀、噪声等现象。 图14 压力分布云图Fig.14 Pressure distribution counters 比较典型阀芯位移下的压力分布:当入口体积流量Q相同时,随着阀芯位移的逐渐增大,K形节流槽的入口压力逐渐降低,压力梯度减小,且压力变化区域逐渐向K形节流槽出口拓展;阀口处局部低压区域面积逐渐缩小,减小了气穴、噪声等现象发生的几率。 比较不同入口体积流量下的速度分布情况:当阀芯位移相同时,随着入口体积流量Q的逐渐增大,K形节流槽入口压力逐渐增大,压力变化梯度增大;K形节流槽出口与阀颈交界处的低压区面积逐渐增大,且最低压力值越来越小。 流体的流动阻力不仅受到速度U和压力梯度▽p的影响,还与它们之间的协同程度有关。流体流动阻力与速度U、压力梯度▽p以及二者夹角余弦值θ成正比例关系,协同角θ越大,流动场协同数值越小,在流动区域内的协同性越弱,进而流动阻力越大。 如图15所示为不同入口体积流量、不同阀芯位移下阀口的场协同角分布云图,结合图13和图14对阀口处的流阻特性进行分析。可以观察到,不同入口体积流量下节流槽阀口处场协同角的分布没有明显变化,即入口体积流量对流体流动阻力没有显著影响。 图15 场协同角分布云图Fig.15 Field synergistic angular distribution counters 协同角较小(小于45°)的部分主要集中在流体进入K形节流槽的入口处,由图14压力分布情况可知,在K形节流槽的入口且未进入节流槽时压力梯度较小,流线分布相对于节流槽内部较疏,因此在进入节流槽前流阻较小。阀腔内流体速度方向变化产生的动能交换及壁面边界层的黏性作用导致入口区域的流动阻力变化,且能量损耗相对较小。由图13速度分布及流线图可知,从节流槽流出的高速附壁射流流入回油阀腔,并与阀腔内的流体发生速度交换,在射流域的左右两侧产生涡流。在节流槽出口区域,大部分场协同角值为30°~60°,流动阻力较小,表明在速度较大的区域,流动阻力也可以相对较小;涡流附近场协同角较大(>70°),流阻较大。在K形节流槽内部区域,靠近阀体壁面区域的场协同角与入口区域的场协同角相近,主要集中在20°~45°;靠近节流槽壁面区域的场协同角较大,主要集中在70°~90°,结合图13速度流线图及图14压力云图可以发现,靠近K形节流槽壁面区域的流线发生大角度弯折,流动方向变化显著,且压力梯度变化较大。 随着阀口开度的增加,节流槽入口处阀口面积逐渐增大,节流槽外壁面高场协同角区域面积逐渐缩小,且逐渐向节流槽入口迁移;等效阀口面积逐渐过渡到环状过流截面,节流槽出口与阀颈交界处场协同角逐渐增大。 综上所述,节流槽内部流动阻力较大的区域主要分布在节流槽入口等效阀口面积、节流槽外壁、阀芯凹角、剧烈涡流等压力梯度变化较大或流线弯折角度较大区域,阀口开度对流动阻力影响较大,入口体积流量对阀内流动阻力没有显著影响。 本研究采用理论分析和数值模拟相结合的方法,对K形节流槽滑阀的面积特性、流场分布及阻力特性进行了综合研究。通过分析得到以下结论: (1) 根据最小过流面计算阀口面积的原则,阀口面积由K形节流槽过流截面、全周端面、环状过流截面共同决定,K形节流槽阀口面积随阀芯位移变化呈线性增长趋势,“K区”和“K+Q区”阀口面积变化各占46.2%和53.8%。 (2) 引入湍流场协同原理,比较速度矢量与压力梯度的协同角,分析流体流过节流槽阀口的局部阻力损失。研究发现:K形节流槽内部流动阻力较大的区域主要分布在节流槽等效阀口面积、节流槽外壁、阀芯凹角及剧烈涡流等压力梯度变化较大或流线弯折角度较大处;随着阀口开度的增大,阀内流动阻力相应减小,且高流动阻力区域逐渐向阀口和阀颈处迁移;入口体积流量对阀内流动阻力没有显著影响。3 数值模拟与试验验证
3.1 数值模拟

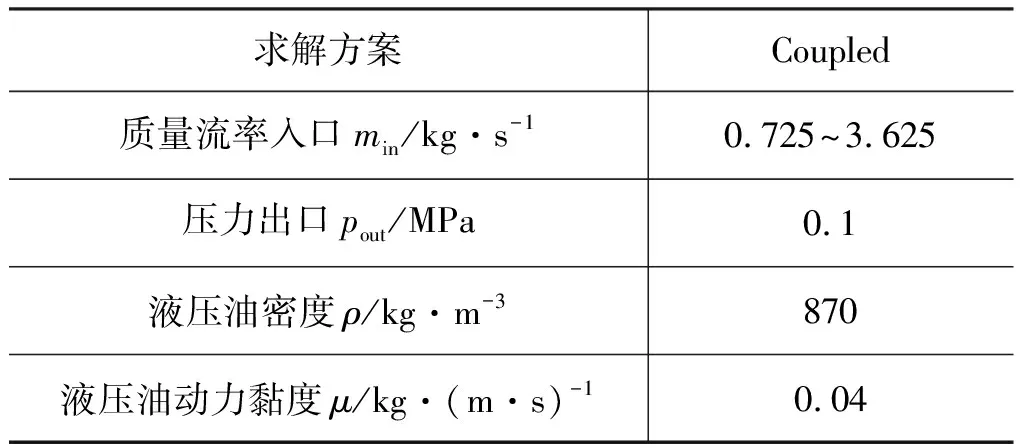


3.2 试验验证


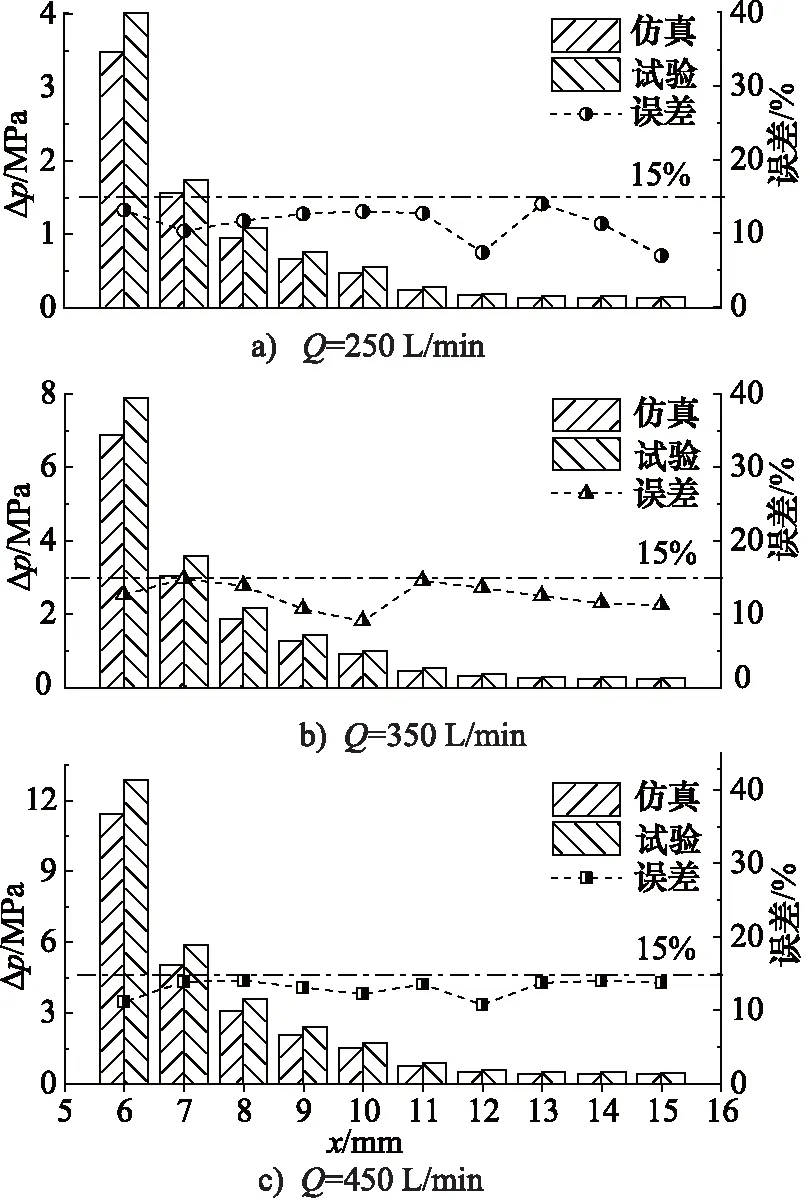
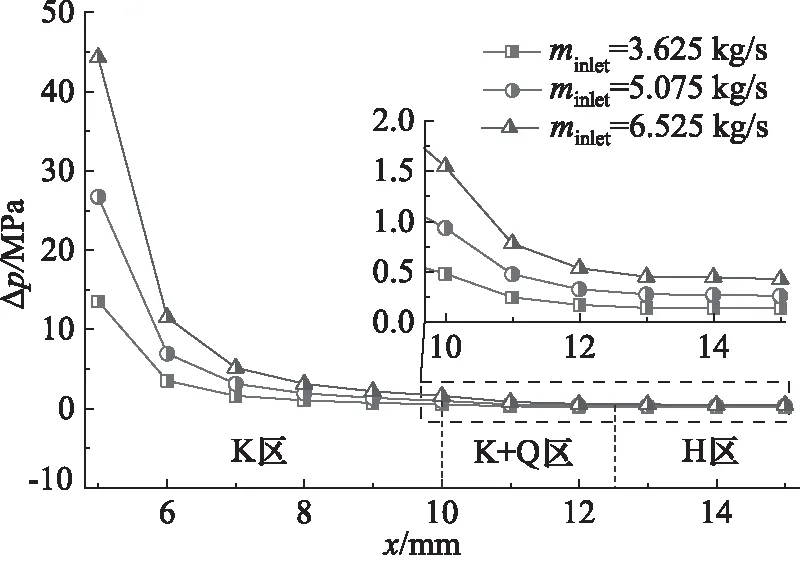
4 K形节流槽阀口流阻特性分析
4.1 流场分布特性分析


4.2 流阻特性分析

5 结论

