基于CFD的液压滑阀阀口处流场研究
王 辉,潘生根(中国民航大学航空工程学院,天津 300300)
基于CFD的液压滑阀阀口处流场研究
王 辉,潘生根
(中国民航大学航空工程学院,天津 300300)
采用CFD方法对一种锥形阀口滑阀内流场进行了数值仿真计算,分析了在固定条件下其阀口处流场分布情况,并从阀口开度及结构参数等方面对影响阀口处流场分布进行了分析比较。研究结果表明:其阀口处流体流动情况复杂,流场在其轴向及径向分布不均衡,受阀口开度及结构参数等方面的影响;可通过优化阀口结构参数,改变阀口开度来改善阀口处流场分布状况,抑制气穴及旋涡的产生与发展,减小压降及能耗。
CFD;锥形阀口;流场分布;阀口开度;结构参数
在液压系统中,用各种液压阀来控制液流的流动方向、压力、流量等,从而控制整个液压系统的全部性能[1]。而液压滑阀是液压系统中使用最广泛的一种基础控制元件。在其工作过程中,阀内的流体流动特性直接影响着元件乃至整个液压系统的性能。特别是当流体流经阀口时,其流动现象复杂,会产生压降和能耗,并使系统发热,若流道设计不好还会引起空化,产生噪声并腐蚀阀芯[2]。因此从流场微观角度对液压油流经阀口时的流场特性进行研究,对改善阀口处的流场特性及提高阀的工作性能具有积极的意义。
CFD技术的快速发展及流场显示技术的进步为深入研究液压元件内部复杂流场提供了有力手段[3]。本文运用CFD软件FLUENT对一种工程机械中常用的锥形阀口滑阀进行流场仿真,分析在固定条件下阀口处流场分布情况,并从阀口开度及结构参数等方面对阀口处流场分布的影响进行了分析研究。近年来,国内外学者对液压滑阀阀口处流场进行了大量的研究[4-6],但大多属于传统圆柱形滑阀,而对多数异形阀口滑阀的研究还较少,特性研究还不够深入、不够完善等,因此本文的研究工作可对异形阀口滑阀的优化设计提供重要的理论依据及实际参考价值。
1 CFD模型及解析假定
1.1 CFD分析模型
模型的建立应尽可能反映计算对象的本质,并能够进行数值解析。本文中的锥形阀口滑阀在尽量反映了滑阀内流道真实结构的基础上给定几何参数,其二维结构简图如图1所示,主要由阀芯和阀体等组成,其中x为阀口开度,β为阀口锥角,α为阀口长度,b为阀杆长度,其他各参数值如图1所示,单位均为mm。从图中可看出此滑阀阀口呈现锥形,在流体流过阀口时能起到导流和节流作用,且其具有流量增益曲线平缓,在一定范围内线性度好,可减小滑阀换向液压冲击、振动等特点而在工程阀领域得到了广泛应用。流体流过阀体流道的三维几何模型用catia建立,由于滑阀内部流动具有对称性,只仿真其中的一半流动区域,以提高计算效率,节省计算机内存。图2为β= 20°、α=6 mm、b=13 mm,x=3 mm时所对应的滑阀流体区域CFD分析模型。

图1 滑阀二维结构简图Fig.1 2-D structure scheme of spool valve

1.2 解析假定
为使数值解析可行,在对实际模型进行仿真计算时必须进行必要的简化和假设。在分析问题的允许计算误差范围内,对本模型做了如下解析假定:
1)假设该锥形阀口滑阀为理想液压滑阀,阀芯与阀体配合精确、无径向间隙、无泄漏。
2)流动介质选用10号航空液压油,密度为850 kg/m3,运动粘度为10 mm2/s。
3)该液压油的压缩性非常小,在计算中可完全忽略其压缩性的影响,为不可压缩的恒定牛顿流体。
4)经计算此模型中的最低雷诺数大于30 000,远大于滑阀阀口处临界雷诺数260,故滑阀内流动状态为湍流,湍流模型采用标准k-ε湍流模型。
5)采用SIMPLE方法对离散方程进行求解,计算残差为0.000 1。
6)与流体接触的边界壁面为静止壁面,进口边界条件为压力入口10 MPa,出口边界条件为标准大气压。
2 网格划分
初始计算网格由GAMBIT软件生成,采用四面体与六面体混合网格划分方法。由于滑阀阀口及流道拐角处压力、速度变化大,为获得更好的求解精度,采用FLUENT的网格自适应功能对初始网格再进行细化处理。
3 仿真结果及分析
3.1 固定条件下阀口处流场仿真结果分析
为分析在固定条件下阀口处流场分布情况,使β=20°、a=6 mm、b=13 mm、x=3.5 mm时对阀进行流场仿真。本文如无特殊说明所有仿真结果中压力单位为Pa,速度单位为m/s。
3.1.1 阀口处压力场分布情况分析
由于阀口区域结构对称,取对称面阀口下方流道区域来分析阀口处轴向压力分布情况,取在轴向离阀口端面左边2 mm处的半圆环流道来分析阀口处径向压力分布情况,结果如图3所示。

图3 阀口区域压力分布图Fig.3 Pressure distribution of valve port domain
从图3(a)中可看出流体流经节流口时,由于节流收缩作用,流速增大压力急剧降低,并在附近形成低压区,远离低压区节流口后方区域压力又逐渐缓慢增加,但由于阀芯凹角处有旋涡的形成,旋涡中心压力降低。从图3(b)中可看出阀口区域径向压力分布呈现从阀口上方至阀口下方,从阀芯壁面至阀体壁面逐渐递减趋势,这是因为在阀口区域形成射流,使得阀芯壁面受到流线的挤压而阀体壁面与流线脱空,流速从阀口上方至阀口下方在逐渐增大。阀口区域这种轴向和径向压力分布的不均衡,将对阀芯的稳态液动力和径向力产生影响。
3.1.2 阀口处速度场分布情况分析
同理取对称面阀口下方流道区域来分析阀口处轴向速度分布情况,取在轴向离阀口端面左边2 mm处的径向半圆环流道来分析阀口径向速度分布情况,结果如图4所示。

图4 阀口区域速度分布图Fig.4 Velocity distribution of valve port domain
从图4(a)中可看出流体在流经节流口时速度急剧增加,并在靠近阀芯壁面处形成高速区,在流过过流断面后速度明显减小,而在阀芯凹角处分布着低速区。从图4(b)中可看出流体在流过节流口时形成射流,且射流角等于阀口锥角,并在过流断面突变处与壁面发生了脱离现象,而在阀芯凹角处还有旋涡生成,在射流区至阀体壁面之间区域存在着回流,回流的存在有利于补充该区域的压力,降低气穴发生的几率。从图4(c)中可看出,从阀口上方至阀口下方的对应区域流速在逐渐增大,且高速区分布在阀芯壁面处,这是由于锥形阀口的导流和在节流口处的节流作用,导致高速射流贴着阀芯壁面流动。
3.2 不同条件下阀口处流场仿真结果分析
3.2.1 阀口开度
为研究阀口开度对阀口处流场分布的影响,保持β=20°、α=6 mm、b=13 mm固定不变,只改变阀口开度x。图5为在阀口开度为1.5 mm、3 mm、4.5 mm、6 mm时所得仿真结果的对称面阀口下方区域流场分布图。
从图5(a)中可看出,随着阀口开度的增加,节流口处的低压区缩小,压力升高,负压消失,整体压力分布趋向均匀,阀口前后压差减小压降降低,并当开口增大到一定时,最低压的位置由节流口处迁移至阀芯凹角旋涡中心,因此可改变阀口开度来改变阀口区域的压力分布状况。从图5(b)中可看出,随着阀口开度的增加,阀口处最大速度在减小,高速区范围在增大,速度分布趋向均匀,这是由于在其他条件不变的情况下,随着阀口开度的增加,节流口不断往阀口端面移动,使流体流过节流口时过流面积增加,节流收缩作用减弱,阀口处流速减小,压力升高。从图5(c)中可看出,随阀口开度的增加,阀口处射流角保持不变且都等于阀口锥角,而阀芯凹角旋涡分布也几乎不变,这是由于锥形阀口的导流作用,使射流始终沿着阀芯壁面流动。
3.2.2 阀口锥角
为研究阀口锥角对阀口处流场分布的影响,保持α=6 mm,b=13 mm不变,开口均为全开状态,只改变阀口锥角β。图6为在阀口锥角β为10°、15°、20°、25°时所得仿真结果的对称面阀口下方区域流场分布图。
从图6(a)中可看出,当阀口锥角较小时阀芯凹角旋涡中心出现负压,而随着阀口锥角的增加,该处压力增大负压消失,阀口其他区域压力也随之增大。从图6(b)中可看出,随着阀口锥角的增加,阀口处最大速度减小,分布趋向均匀,这是因为在其他条件不变的情况下,随着阀口锥角的增大,节流口至阀芯壁面的距离增加,导致流体流过节流口时的过流面积增加,节流收缩作用减弱,使得阀口处流速减小,压力升高。从图6(c)中可看出,随着阀口锥角的增加,阀口处射流角也增加且等于阀口锥角,而阀芯凹角旋涡区却逐渐缩小。

图5 不同开度的对称面阀口下方区域流场分布图Fig.5 Flow field distribution of the symmetry surface of valve port lower domain at different openings
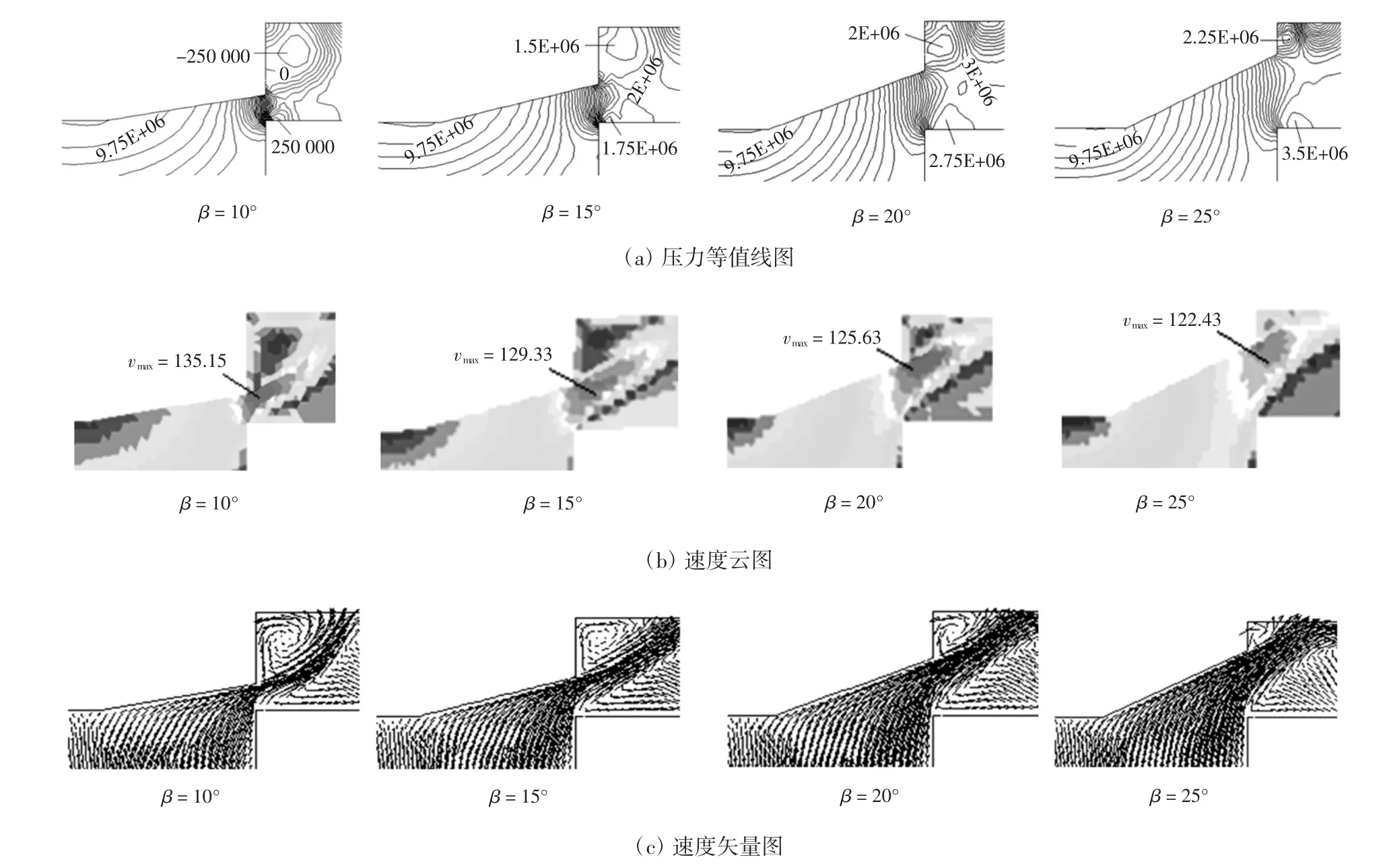
图6 不同锥角的对称面阀口下方区域流场分布图Fig.6 Flow field distribution of symmetry surface of valve port lower domain at different cone angles
3.2.3 阀口长度
为研究阀口长度对阀口处流场分布的影响,在阀口开度和锥角相同的情况下,增大阀口长度a的同时相应减小阀杆b的长度,这样保证出油腔结构位置的不变,避免其他因素的影响。图7是当β=20°,x= 2.5 mm,a、b分别为4 mm、15 mm;6 mm、13 mm;8 mm、11 mm;10 mm、9 mm时所得仿真结果的对称面阀口下方区域流场分布图。

图7 不同长度的对称面阀口下方区域流场分布图Fig.7 Flow field distribution of the symmetry surface of valve port lower domain at different lengths
从图7(a)中可看出,随着阀口长度的增加,节流口处右边区域低压区明显缩小,压力升高,且最低压由负压升高到正压,而节流口处左边区域压力分布几乎保持不变。从图7(b)中可看出,随着阀口长度的增加,阀口处最大速度减小,这是由于在其他条件不变的情况下,随着阀口长度的增加,虽节流口处的过流面积始终未变,但阀口长度的增加,对粘性流体流动的阻碍作用增强,使得阀口处最大流速减小,最低压力升高。从图7(c)中可看出,随阀口长度的增加,阀口处射流角保持不变,而阀芯凹角旋涡区逐渐变小甚至消失。
4 流场仿真分析
通过对一种锥形阀口滑阀的流场仿真,分析了其阀口处压力场、速度场及旋涡分布情况,并从阀口开度及结构参数等方面对影响阀口处流场分布进行了比较分析,可以得出以下结论。
1)阀口处流体流动情况复杂,存在高速射流、分离流、回流、旋涡及局部低压现象,甚至还有气穴气蚀发生的可能。
2)压力场和速度场在阀口处分布不均衡,在轴向及径向分布呈现一定的规律。
3)阀口处压力场分布的影响:随阀口开度、长度和锥角的增加,阀口处低压区缩小,最低压力值升高,阀口前后差压减小,压降降低。
4)阀口处速度场分布的影响:随阀口开度、长度和锥角的增加,阀口处最大速度减小,分布趋向均匀,且射流角基本等于阀口锥角,阀口开度及长度对射流角几乎无影响。
5)阀口处旋涡分布的影响:随阀口长度和锥角的增加,阀芯凹角旋涡区逐渐减小甚至消失,而阀口开度对其旋涡分布几乎无影响。
5 结语
在此种锥形阀口滑阀的设计过程中,可通过优化阀口结构参数,改变阀口开度来改善阀口处流场分布状况,抑制气穴及旋涡的产生与发展,减小压降及能耗。考虑到此种阀的特殊性及CFD理论模型与实际情况的差异,在具体优化设计过程中,还应采用相应的实验方案对优化模型进行结果验证分析。而在采用理论结论优化时,当阀口结构参数在互不关联范围内时,取各参数范围内的最大值即最优值;而当阀口结构参数在互关联范围内时,应多次取其优值,并将各次优化结果进行对比分析,从而得出阀口结构参数的最佳优化匹配。
[1]路甬祥.液压气动技术手册[M].北京:机械工业出版社,2001.
[2]高小瑞.基于Fluent的液压滑阀内部流场的数值模拟[J].机械管理开发,2009,24(5):49-53.
[3]郑淑娟,刘楷安,孙雪丽.基于CFD的液压锥阀内部流场的数值模拟分析[J].华北水利水电学院学报,2008,29(2):56-58.
[4]POUNTNEY D C,WESTON W,BANIEGHBAL M R.A numerical study of turbulent flow characteristics of servo valve orifices[J].Proc Instn Mech Engrs:Part A,1991,205:139-147.
[5]BORGHI M,CANTORE G,MILANI M,et al.Analysis of hydraulic components using computational fluid dynamics models[J].Proc Instn Mech Engrs:Part C,1998,212:619-629.
[6] 贾文华,殷晨波.阀口气穴流场的数值模拟与实验研究[J].液压与气动,2010(4):14-17.
Research of flow field in orifice of hydraulic spool valve based on CFD
WANG Hui,PAN Sheng-gen
(College of Aeronautical Engineering,CAUC,Tianjin 300300,China)
The numerical simulation computation of flow field in a conical spool valve was carried,which was based on CFD approach.The simulation results of flow field distribution under fixed condition were analyzed,and the influence of opening and structural parameters of valve port on the flow field distribution in valve port were also analyzed and compared.The results show that the fluid flows complicatedly in valve port,the flow field distribution is uneven in the axial and radial and affected by the opening and structural parameters of valve port;optimizing the structural parameters of valve port and changing the valve opening can improve the flow field distribution in valve port,prevent the cavitation and the vortex forming and developing,reduce pressure loss and energy consumption.
CFD;conical valve port;flow field distribution;valve opening;structural parameter
TP391
A
1674-5590(2013)01-0067-06
2012-06-06;
2012-09-05
中央高校基本业务费专项基金项目(ZXH2010D023)
王 辉(1966—),男,辽宁本溪人,教授,博士,研究方向为飞行系统仿真.

