柔性网展开过程仿真模拟及试验研究

张朝衍,杨跃能,步晓童

(国防科技大学 空天科学学院,湖南 长沙 410073)

柔性捕获指通过柔性网、口袋、柔性绳索等装置实现对目标的抓捕,不需要考虑特定的抓捕位置,可适应不同形状和尺寸的目标抓捕。此外,柔性捕获具有非致命性,作用面积较广、距离较远等特点,在复杂的城市环境中应对突发事件可以有效控制局面,同时避免过度伤害。在柔性网、口袋、柔性绳索等多种不同的装置中,柔性网的使用最为广泛,被广泛运用于无人机抓捕[1]、非致命武器[2]、空间捕获[3-5]和防护式拦截[6]等领域。

对于柔性体的展开过程许多学者都进行了研究。柔性网展开的动力学建模方法通常为先对绳网进行离散化处理,再使用有限元方法进行动力学建模。常用的有限元方法有集中质量法和绝对节点坐标法等。卞伟伟等[5]针对柔性拦截网空中展开的动力学过程,提出采用滞空时间、最大开网面积、有效拦截面积作为柔性拦截网开网效果的衡量指标,分析了影响柔性拦截网开网效果的主要因素。为了分析柔性拦截网开网过程,建立了柔性绳索非线性动力学模型,采用拉格朗日网格对网体的变形和位移进行描述,并模拟计算了网体展开过程[7],同时基于仿真数据分析了不同的发射条件对展开性能的影响,但是并没有进一步的试验验证。万家宁等[8]则使用有限元方法模拟了该过程,并进行了网体的发射试验。文献[9-10]使用绝对节点坐标法对网体的绳段单元进行了模拟。WILLIAMS等[11]基于集中质量法建立了集中质量弹簧模型来模拟柔性绳索的离散模型,加入空气阻力影响进行了动力学建模,并且分析了柔性网的展开动力学特性。王晓慧等[12]采用容错值函数来描述飞网展开捕获性能,并建立了以容错值为优化目标的优化模型,同时验证了该优化模型的可行性。李京阳等[13]研究了不同工况下抛射参数对展开过程的影响,研究结果表明柔性网的抛撒角度是影响其展开的关键因素,还建立了不同折叠方式的柔性网有限元模型,并分析了折叠方式对展开效果的影响。本文将基于集中质量模型从模型设计、仿真计算和试验验证三个方面研究超低空环境下柔性网的动力学响应特征,得到了柔性网捕捉性能受到各方面因素影响的一般性规律。

1 柔性网发射过程及评价指标

1.1 柔性网的发射过程

柔性网的构型主要为辐射型以及网格型。本文采用网格型的柔性网为例对柔性网的展开发射过程进行研究。柔性网的具体构型及尺寸如图1所示,图2为发射装置的示意图。

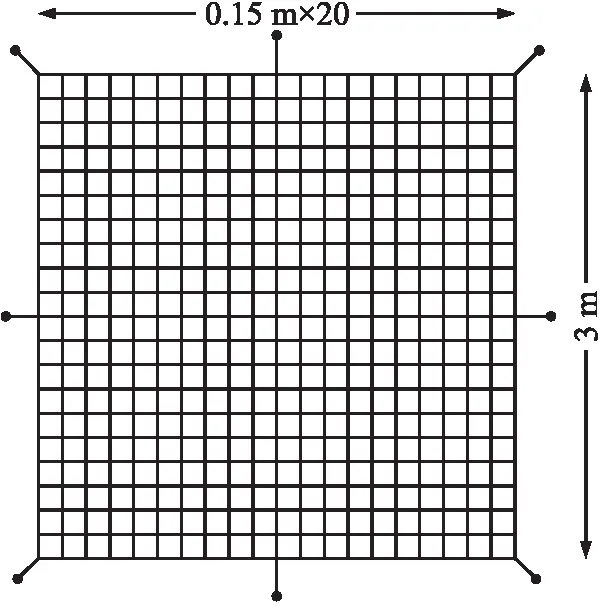
图1 四边形柔性网Fig.1 Quadrilateral flexible net

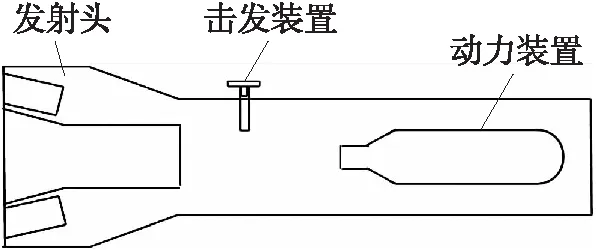
图2 发射装置示意图Fig.2 Schematic diagram of launch device

首先建立以发射装置轴线为z轴,发射头一侧所在平面与z轴交点为原点的直角坐标系。柔性网的发射过程示意图如图3所示。

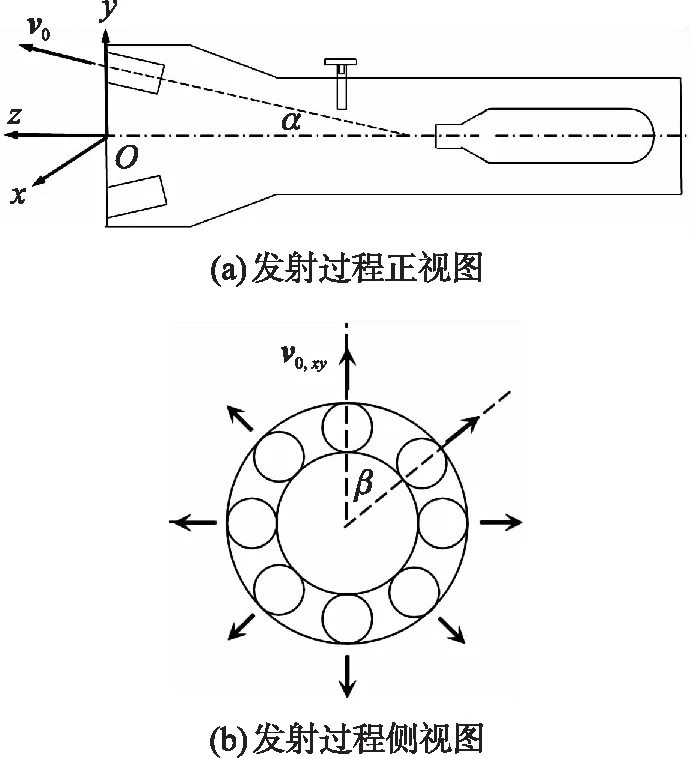
图3 发射过程原理示意图Fig.3 Schematic diagram of the launch process principle

网体及质量块装载于发射头中,击发装置控制动力装置启动,动力装置提供推力将质量块及网体推射出发射头。

质量块受到推动,获得与储存仓轴线平行的初始速度v0。由于8个质量块存储仓的轴线与发射装置轴线存在一定角度α(见图3(a)),质量块的初始速度在Oxy平面上的分量为v0,xy,大小为v0sinα,相邻质量块分速度夹角为展开角β(见图3(b))。这使得质量块将在飞行的过程中于Oxy平面作放射状运动,从而将网体牵引展开。

1.2 柔性网发射过程的评价指标

柔性网的构型、材料有多种选择,为了快速得到符合应用场景要求的柔性网设计,需要一套指标对柔性网的性能进行评价。柔性网的展开过程有如下规律:展开初期质量块呈放射状远离,在经过一定时间之后受到绳网约束相互靠近。在此过程中捕获面积S的变化规律为先变大再变小。捕获过程网体变化规律见图4。

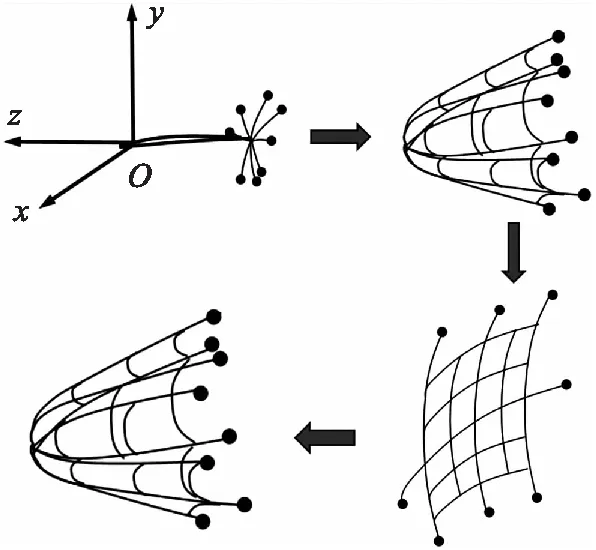
图4 发射展开过程网体变化Fig.4 Changes in the network during the deployment process

根据以上对柔性网的特性及捕获过程的分析,本文提出了四项柔性网的评价指标。

①最快展开时间。

当柔性网展开面积达到0.5 m2时,此时柔性网具备捕获能力。从展开到捕获面积S达到0.5 m2所需时间为最快展开时间tf。

②最大展开面积。

S为随时间变化的变量,S在捕获过程中所取到的最大值Smax为最大展开面积。

③有效面积时长。

捕获过程中,S随时间变化的规律是先变大再变小。在此过程中S取值在某一时间段内均大于0.5 m2,该时间段称为有效面积时长te。

④作用距离。

柔性网需要一定时间和空间进行展开,捕获装置需要和目标保持一个最小距离Dmin,该距离的大小为网体速度在z轴的分量vz从零时刻到t=tf时对时间的积分:

(1)

式中:v为网体的速度矢量,iz为z轴的单位方向矢量。

以上四项指标可以对柔性网的捕获能力进行评价,在实践中为不同柔性网的使用和选择提供指导和参考。

2 柔性网动力学模型

2.1 基本假设及建模原理

建立柔性网展开过程动力学模型的基本假设[14-15]如下:

①不考虑柔性网结构中的弯曲挠性;

②忽略绳段间的接触效应;

③柔性网展开过程中质量块视为质点。

针对柔性网非线性、柔性等特性,采用集中质量弹簧模型对绳段单元进行描述,如图5所示。

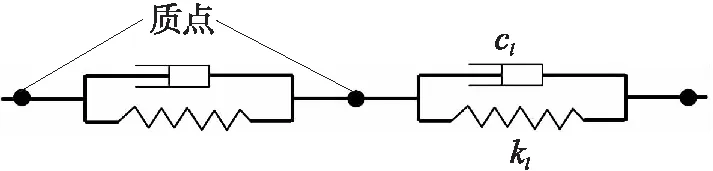
图5 集中质量弹簧模型Fig.5 Lumped mass spring model

将若干个绳段的集中质量模型相连得到柔性网的动力学模型,如图6所示。将柔性网模型中的质点编号为Pi(i=1,2,3,…),将绳段单元根据两端质点Pu,Pv命名为ξuv。

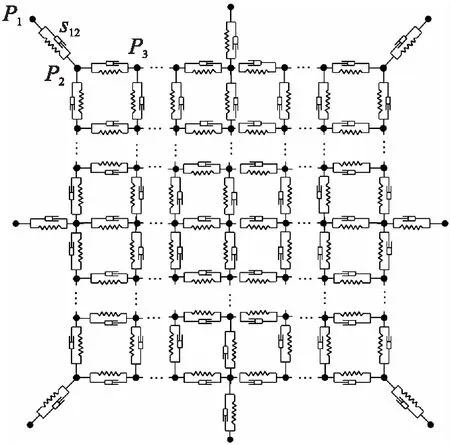
图6 柔性网集中质量模型Fig.6 Lumped mass model of flexible net

2.2 动力学分析

根据集中质量单元的假设,绳段间的张力由弹簧的弹性力和阻尼器的阻尼力构成。绳段ξuv的张力[16-18]为

(2)

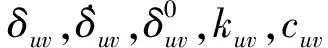
δuv=‖ru-rv‖

(3)

式中:ru,rv为绳段两端质点Pu,Pv的位置矢量。

(4)

式中:euv为Pu指向Pv的单位方向矢量。

绳段单元受到的外力有重力和气动阻力。ξuv所受的重力为

(5)

式中:ruv和muv分别为绳段中点的位置矢量和绳段质量。

气动阻力[19]为

(6)

绳段所受的外力为

(7)

质点Pi的动力学方程为

(8)

式中:Ti,Fi分别为质点Pi受到的等效张力和等效外力。

3 柔性网展开过程仿真计算

3.1 仿真计算过程

柔性网的绳索部分只能受拉力而不能受压力,牵引质量块视作质点,根据两者的特性选取合适的单元类型。建模过程中单元实常数、材料密度等参数见表1所示。

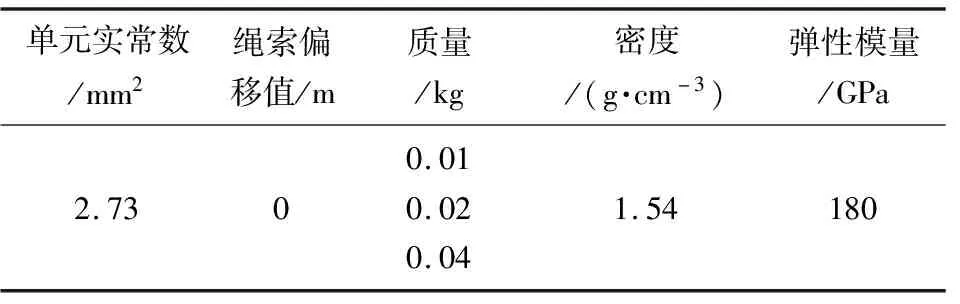
表1 ANSYS建模参数Table 1 ANSYS modeling parameters

折叠状态的设置:根据实践结果,在发射初始阶段,网体的质量块获得较大速度,将剩余部分从发射头中牵引出,网体将呈现收束的折叠状态,如图7所示。

图7 柔性网发射初始阶段Fig.7 Initial stage of flexible network launch

通过两次仿真,模拟对完全展开的网体模型进行折叠,将折叠后的网体模型的各个单元的坐标输出为折叠的初始状态。

①第一次模拟折叠,将网体收缩折叠,第一次模拟折叠状态如图8所示。

图8 第一次折叠效果Fig.8 The effect for the first fold

②第二次模拟折叠,牵引网体形成锥形折叠状态(见图9)。此时网体折叠装填较为接近实际发射过程中的折叠状态。

图9 第二次折叠效果Fig.9 The effect for the second fold

③最后,将节点坐标信息输出,作为最终仿真计算的初始折叠状态。

3.2 仿真计算及动力学响应分析

对仿真得到的各项数据进行分析,得到柔性网展开指标对不同影响因素的响应特性。部分仿真过程见图10。

图10 仿真计算过程Fig.10 Simulation calculation process

①质量块质量占比的影响。

为保证展开效果,模拟过程采取0.9以上的质量占比。计算结果见图11。最大展开面积(Smax)和有效面积时长(te)都与质量块占比成正相关;最快展开时间(tf)与质量占比成负相关。在质量占比达到98%之前,Dmin随质量占比增大而增大。

图11 质量占比对网体指标的影响Fig.11 The impact of quality proportion on network indicators

②质量块初速大小的影响。

质量块的初始速度的改变对网体指标的影响结果见图12。随着质量块初始速度的增大,Smax和Dmin的变化呈现随机波动的特征,并且波动的范围在最大值的10%以内。tf和te随初始速度的变化规律接近指数型变化。在速度趋近于0时,两项指标迅速增加,速度增大时两项指标随速度增大而减小。

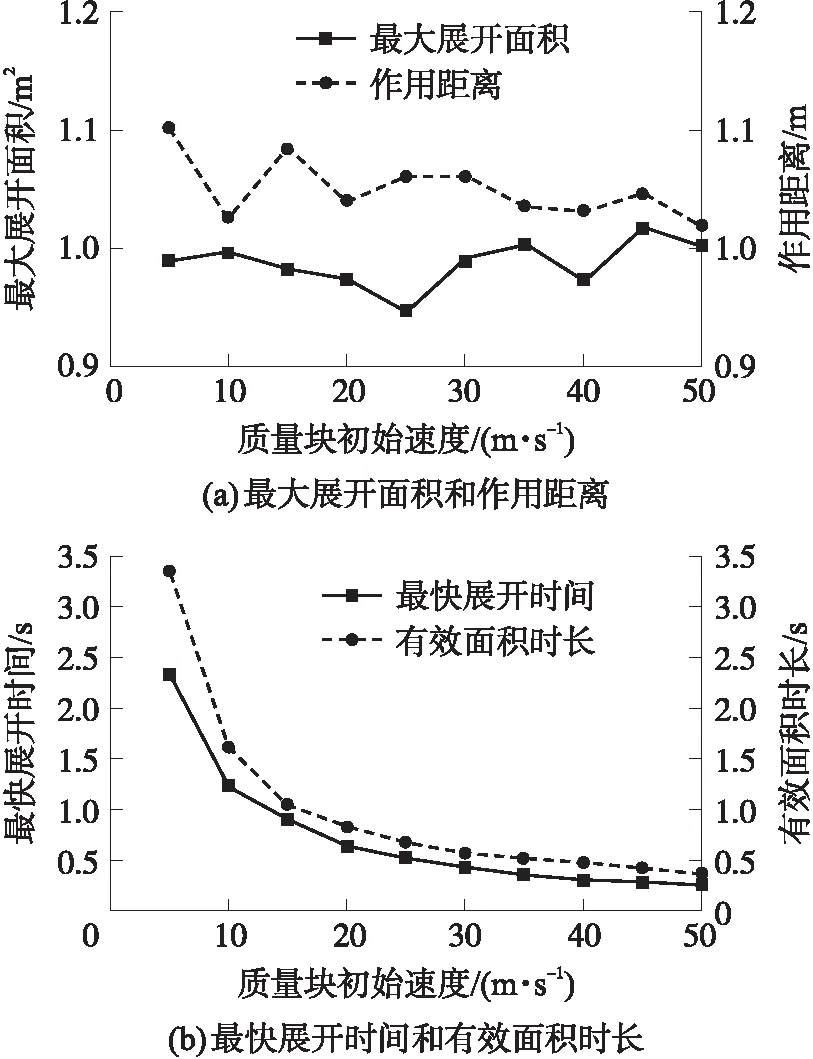
图12 初始速度对网体指标的影响Fig.12 The impact of initial velocity on network indicators

③展开角的影响。

展开角的大小取决于发射装置的设计,受限于机械结构,展开角的大小不超过45°。展开指标对展开角的响应结果见图13。Dmin和tf随展开角的增大而减小;最大展开面积随之增大。而有效面积持续时间则随展开角的增大先增大后减小。在展开角小于20°的时候,增大展开角对于改善网体捕获性能的作用更为明显。

图13 展开角对网体指标的影响Fig.13 The impact of unfolding angle on network indicators

4 柔性网捕获过程试验研究

4.1 实验条件

为验证动力学模型的可靠性以及仿真结果的准确性,选取仿真计算中的一组初始条件进行验证(见表2),试验设备见图14。

表2 试验参数条件Table 2 Test parameter conditions

图14 试验设备Fig.14 Test devices

4.2 试验过程

使用柔性网发射装置发射柔性网捕捉无人机,并使用高速摄像机对过程进行记录。通过质量块在每张图片中的位置变化可以计算出质量块的速度以及位移大小,再得出试验所用的柔性网各项指标。

4.3 试验结果及分析

试验过程的部分记录图像见图15。由于试验的拍摄角度位于侧面,难以对网体展开面积进行测量,这里使用质量块在重力方向上的相对位移作为等效变量来判断网体的展开状态。试验结果与仿真结果数据对比见表3。结果显示,实际展开时间、最大相对位移和有效时长的相对误差较小,均在10%左右。而作用距离的误差较大,相对误差达到了31.2%。这样的结果说明动力学模型在一定程度上具有可靠性。其误差来源推测为:提出的假设忽略了柔性绳索之间的接触效应。实际过程中该效应导致网体的展开晚于仿真模拟的过程。

图15 飞行过程图片Fig.15 Pictures for the flying process

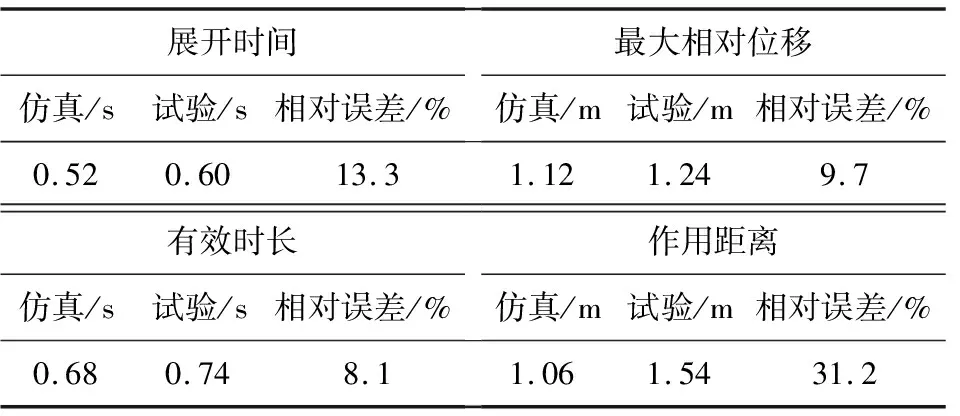
表3 仿真与试验数据对比Table 3 Comparison of simulation and experimental data

5 结束语

本文构建了一个评价体系,对柔性网的展开性能进行评价。基于集中质量假设和有限元方法,对一种网格型的柔性网展开了建模和仿真模拟。在仿真计算结果的基础上,结合提出的评价体系,分析了质量块质量占比、质量块初始速度和展开角3个不同的初始条件对网体展开性能的影响。选取了一种初始条件进行了发射试验,各项实验数据的最大相对误差最大为31.2%,最小为8.1%。