电磁轨道炮导轨身管系统动力学分析

江镇宇,于海龙,何 斌,靳 展

(南京理工大学 发射动力学研究所,江苏 南京 210094)

电磁轨道炮发射过程中,伴随着电枢的高速运动,复杂环境载荷将会对装备造成多场耦合、超强瞬态、幅值巨大的冲击作用[1-2]。为了设计出既能保证枢轨间有足够的接触力,又能保证不会因温度过高、受力过大而导致系统结构破坏,研究发射状态下的导轨身管发射装置动力学非常必要。

多体系统传递矩阵法(multibody system transfer matrix method,MSTMM)是近二十多年来提出并不断完善的一种多体系统动力学数值计算方法。利用MSTMM对多体系统动力学进行数值计算时无需建立系统总体动力学方程,所涉及的矩阵阶次与系统的自由度数无关,可显著提高多体系统动力学数值计算效率,为复杂机械系统动力学的快速数值分析与优化设计带来了方便[3]。本文采用MSTMM求解电磁轨道炮系统导轨身管的振动特性及动态响应。

为了保证电磁轨道炮的射击精度,发射过程中轨道的位移要控制在一定范围内。目前,研究人员对于电磁炮系统建模与数值仿真主要聚焦于电磁炮的发射机理,因此主要仿真分析电枢轨道或者电枢线圈系统。TZENG等[4]将轨道建模为弹性地基上的欧拉梁模型;刘文等[5]利用分离变量法和计入阻力的拉格朗日方程,推导出轨道受任意指数函数磁压力的控制方程的解析解;文献[6]给出了轨道的机电耦合动力学方程,分析了轨道对运行电磁力的强迫响应;LEE等[7]利用弹性基础上的Timoshenko梁模型分析了电磁炮轨道在移动电枢和电磁力作用下的动态响应;田振国[8]得到发射状态下复合导轨的动态响应,分析发现电枢压力对轨道变形的影响远大于轨道间斥力的影响;CHE等[9]建立了电磁炮轨道在不同约束条件和预紧力作用下的三维有限元模型,讨论了不同约束和预紧力对固有频率、振形函数的影响;XU等[10-11]建立了轨道炮系统机电耦合参数振动方程,发现随着动态电流幅值和电枢与炮口距离的增大,系统振动的不稳定区域增大;蔡喜元[12]将轨道炮发射身管简化为弹性基础上双层欧拉梁模型,分析了不同结构参数和材料性能对身管振动特性的影响机理;DU等[13-14]基于弹性基础上的欧拉梁理论提出了考虑弹丸运动的轨道振动模型,给出了枢轨动态电磁接触力的解析模型;ZHANG[15-16]利用非线性有限元模型研究电磁轨道炮导轨的动态特性,详细分析了脉冲电源参数和轨道尺寸对电磁轨道炮性能的影响;LU[17]分析了连续放电和连续发射条件下导轨的内弹道性能,确定了轨道的动态响应不受上一次发射的影响的发射间隔为1 s;何威等[18]求解了悬臂式双层弹性基础梁模型在电磁力和电枢力作用下的位移和应力的解析解,并用ANSYS数值分析结果验证了解析解的正确性;沈剑[19-20]基于Timoshenko梁建立了电磁炮发射过程的弹炮刚柔耦合多体动力学模型,获得了在考虑身管和导轨柔性变形时超高速弹丸膛内的基本动力学特性。

目前建立的电磁轨道炮导轨身管模型大多忽略了上下导轨结构实际情况中的非对称性,同时将导轨外支撑身管简化为边界条件,与实际情况有一定差异。本文考虑上下导轨弹性支撑参数、空间位置及力学参数非对称性的影响,将上下两根导轨视为平面横向振动的梁,导轨至轨道炮外层的其余部分视为两弹性支撑作用下的横向振动梁,三梁之间通过分布弹性作用耦合;电路电源提供的脉冲电流在枢轨求解域内传导并感应出磁场,利用毕奥-萨伐尔定律获得域内电磁规律,进而得到导轨-导轨及导轨-电枢间的电磁力;利用MSTMM,以电磁力为激励源,推导三梁模型系统的动力学方程,利用模态叠加法求解导轨身管系统在重力及时变电磁力作用下的动态响应。

1 导轨身管振动特性

1.1 导轨身管系统振动模型

典型电磁轨道炮身管横截面如图1所示。电磁轨道炮炮身一般由上下导轨、封装、支撑体、填充体和复合材料组成。将外层复合材料、封装、填充体和支撑体合称为身管。为了便于分析,做如下基本假设:

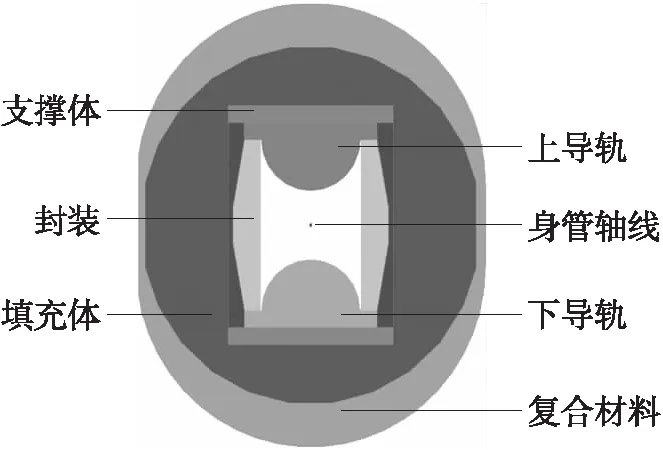
图1 某型电磁轨道炮炮身横截面示意图Fig.1 Schematic diagram of the cross-section of a certain type of electromagnetic railgun barrel

①由于通常导轨和身管的长细比较大(长度与特征宽度之比大于150),假设将其建模为Euler-Bernoulli梁,忽略横向剪切变形的影响;

②由于封装的紧密支撑,忽略导轨身管的轴向位移;

③将导轨与身管间的弹性相互作用视为分布弹簧;

④考虑实际系统上下导轨结构的非对称性。

将导轨身管系统按照连接状态分为五部分,以一体化发射单元的运动方向作为系统各部分之间的传递方向,根据多体系统传递矩阵法“体”和“铰”统一编号的原则,地面边界编号为0,系统各部分依次从1到5进行编号。上下导轨与身管间的支撑体看作是分布弹簧,将地面支撑视为作用在身管特定位置处的弹性支撑力,建立电磁轨道炮导轨身管三梁发射动力学模型,如图2所示。图中,m1,m2,m3分别为上导轨、身管、下导轨的线质量;E1I1,E2I2,E3I3分别为上导轨、身管、下导轨的横截面抗弯刚度;L1,L2,L3分别为系统第一部分、第二部分、第三部分的长度;y1(x,t),y2(x,t),y3(x,t)分别为上导轨、身管、下导轨的挠度;k1为上导轨与身管间弹性刚度;k2为下导轨与身管间弹性刚度;k3为身管与地面间支撑刚度。

图2 某型电磁轨道炮导轨身管三梁发射动力学模型Fig.2 Launch dynamics model of a certain type of electromagnetic railgun rail barrel

1.2 导轨身管系统传递矩阵

选取模型中每根梁物理坐标下的状态矢量为(yθzmzqy)T。y为横向位移在惯性系中的坐标,θz为轴线绕z轴的角位移,mz为横截面所受弯矩,qy为横截面所受剪力。无阻尼自由振动导轨身管系统的响应可由模态叠加求解,若某阶模态下系统固有频率为ω,则对应状态矢量可表示为

(1)

式中:Y,Θz,Mz,Qz为模态坐标下的状态矢量,分别对应物理坐标下的状态矢量;下标j=1,2,3,分别代表上导轨、身管和下导轨。则导轨身管系统对应模态坐标下的全部状态矢量可定义为

Z=(Y1Θz1Mz1Qy1Y2Θz2Mz2
Qy2Y3Θz3Mz3Qy3)T

(2)

系统1,3,5部分导轨身管横向自由振动微分方程为

(3)

由材料力学关系,可得:

(4)

将式(3)和式(4)整理成矩阵形式:

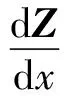
(5)

矩阵A的表达式为

根据式(5)的解,输入端状态矢量ZI与输出端状态矢量ZO之间的传递方程,可写为

ZO=eAxZI=UZI

则系统1,3,5部分的传递矩阵为

U1=U3=U5=U=eAx

(6)

系统2,4部分对应的虚拟元件仅与身管发生相互作用,其弹性点支撑的传递矩阵可写为

(7)

导轨身管系统总传递矩阵可通过系统各部分的传递矩阵按照传递方向依次连乘得到,系统输入端状态矢量ZI1,系统输出端状态矢量ZO5,由总传递矩阵可得系统总传递方程为

ZO5=U5U4U3U2U1ZI1=UallZI1

(8)

导轨身管系统自由端边界条件为

(9)

将三梁系统两端边界条件(9)代入系统总传递方程(8),求得系统在两端自由状态时的固有频率,进而得到各阶频率下输入端完整的状态矢量,利用系统各部分的传递矩阵,便可求得在对应频率下系统任意位置的状态矢量。

2 导轨身管系统动态响应

在电磁发射过程中,导轨受到时变电磁载荷和电枢移动载荷作用,本节将采用增广特征矢量和系统的固有振动特性,建立导轨身管系统在外界激励下的动力学方程,研究系统动态响应。

2.1 模态叠加法

电磁轨道炮导轨身管系统体动力学方程为

Mvtt+Kv=F

(10)

式中:M=diag(M1,M2,M3);K=diag(K1,K2,K3),v=(v1v2v3)T,F=(F1F2F3)T。M,K为增广算子;v为导轨身管系统位移坐标列阵;F为导轨身管系统所受外力列阵;Mi,Ki,vi,Fj(j=1,2,3)分别为上导轨、身管、下导轨的质量参数矩阵、刚度参数矩阵、位移列阵、外力(含外力矩)列阵。

定义导轨身管系统的增广特征矢量为系统线位移列阵所对应的模态坐标列阵,即增广特征矢量V为

(11)

式中:上标k为模态阶数。

由于导轨身管系统三梁动力学模型是由连续体元件构成,所以对应的增广特征矢量Vk的元素应包含系统各阶固有频率所对应的模态。利用增广特征矢量Vk,导轨身管系统动力响应可表示为

(12)

式中:qk(t)为k阶模态下的广义坐标。

将式(12)代入系统体动力学方程(10),得:

(13)

同时计算上式两边和第p阶增广特征矢量Vp的内积,根据增广特征矢量的正交性条件:

〈MVk,Vp〉=δk,pMp, 〈KVk,Vp〉=δk,pKp

式中:δk,p为Kronecker函数。可得:

(14)

式(14)即为广义主坐标下的导轨身管系统强迫振动的运动微分方程,逐个求解可得t时刻对应的广义坐标qp(t),将所求结果代入式(12)即可得到导轨身管系统在指定外力作用下的动态响应。

2.2 导轨身管系统静位移

在重力的作用下,发射前导轨身管在铅垂平面内已经弯曲,其静变形将会影响一体化发射单元在膛内的运动。在研究计算一体化发射单元的起始扰动时,需要计算重力引起的导轨身管的静变形。

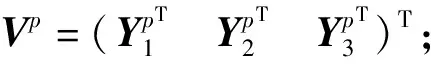
M=diag(m1,m2,m3)

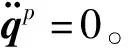
(15)

模态质量Mp与广义力Fp表达式分别为

(16)

(17)

解算出各阶模态下对应的广义坐标qp(t),代入式(12),利用模态叠加法即可求得导轨身管三梁系统在重力作用下的静位移。

2.3 导轨所受电磁力

要在短时间内使电枢获得较高初速,需要在电枢上作用很大的电磁力,而其大小正比于导轨中电流的平方。目前工程中获得一定持续时间的大电流时,最常见的方法是将多个脉冲电流合成得到较宽的电流宽度,合成的电流可简化为如图3所示。

图3 多脉冲合成电流示意图Fig.3 Schematic diagram of multi-pulse synthetic current

合成电流第一阶段可视为按正弦规律增大,第二阶段可视为恒定,第三阶段可视为按指数规律衰减,整个电流过程用函数表示为[21]

(18)

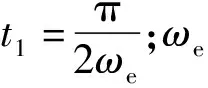
本文考虑电流在导轨与电枢中的分布情况,假设导轨和电枢中电流分布为线电流模型,将上下导轨及电枢分别看成一根载流直导线,忽略电流的趋肤效应,如图4所示。

图4 某型电磁轨道炮导轨电流示意图Fig.5 Schematic diagram of rail current of a certain type of electromagnetic railgun

空间中一根载流直导线在距离其为r的任意点(x,y)处产生的磁感应强度为

(19)

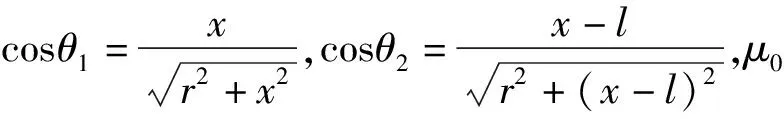
流经上导轨的电流在下导轨位置处产生的磁感应强度为

(20)

流经电枢的电流在下导轨位置处产生的磁感应强度为

(21)

对于平面运动模型,只考虑导轨间y方向的电磁载荷:

(22)

导轨受到电枢电流产生磁场引起的y方向电磁载荷为

(23)

因此,下导轨上受到的总电磁载荷为

Fr=Frr+Far=(Krr+Kar)I2=KrI2

(24)

2.4 导轨身管系统动态响应

系统动力响应物理坐标、第p阶增广特征矢量及对应的增广算子M与求解导轨身管系统静位移时一致,系统对应外力列阵更新为F=(Fr+m1gm2g-Fr+m3g)T,对应的广义力为

(25)

将式(16)、式(25)代入式(14),求解导轨身管系统动力学微分方程,解得广义坐标qp(t),经过模态叠加得到导轨身管系统动态响应,电磁轨道炮导轨身管系统动力学分析流程如图5所示。

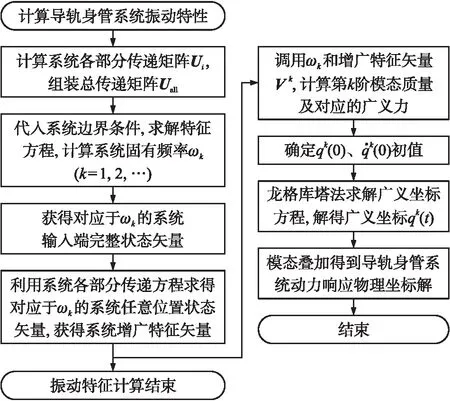
图5 电磁轨道炮导轨身管系统动力学分析流程图Fig.5 Flow chart for dynamic analysis of rail barrel system of electromagnetic railgun

3 仿真计算

3.1 导轨身管系统振动特性

本文以某型电磁轨道炮为例,导轨与身管的间距h=0.1 m,系统其他相关的计算参数见表1。利用商业有限元软件Comsol对导轨身管系统振动特性进行仿真验证,建立导轨身管系统有限元模型,如图6所示,身管与上下导轨间的联接条件设置为弹性薄层,在身管特定位置处设置两个弹性基础模拟地面支撑,采用三角形单元划分网格,共划分5 108个单元。计算导轨身管系统前8阶固有频率,计算结果见表2。

表1 电磁轨道炮导轨身管系统主要参数Table 1 Main parameters of electromagnetic rail gun rail barrel system

图6 电磁轨道炮导轨身管系统有限元模型Fig.6 FEM model of guideway barrel system of electromagnetic railgun

表2 导轨身管三梁系统固有频率Table 2 Natural frequency of three-beam system of guide rail tube

由表2中数据可以看出,两种方法计算结果高度一致,验证了MSTMM求解导轨身管系统固有振动特性的精确性,且MSTMM的计算时间为1.315 s,有限元方法的计算时间为8.931 s,利用MSTMM可以大幅提高计算速度。本文给出导轨身管系统前六阶模态振型,如图7所示。

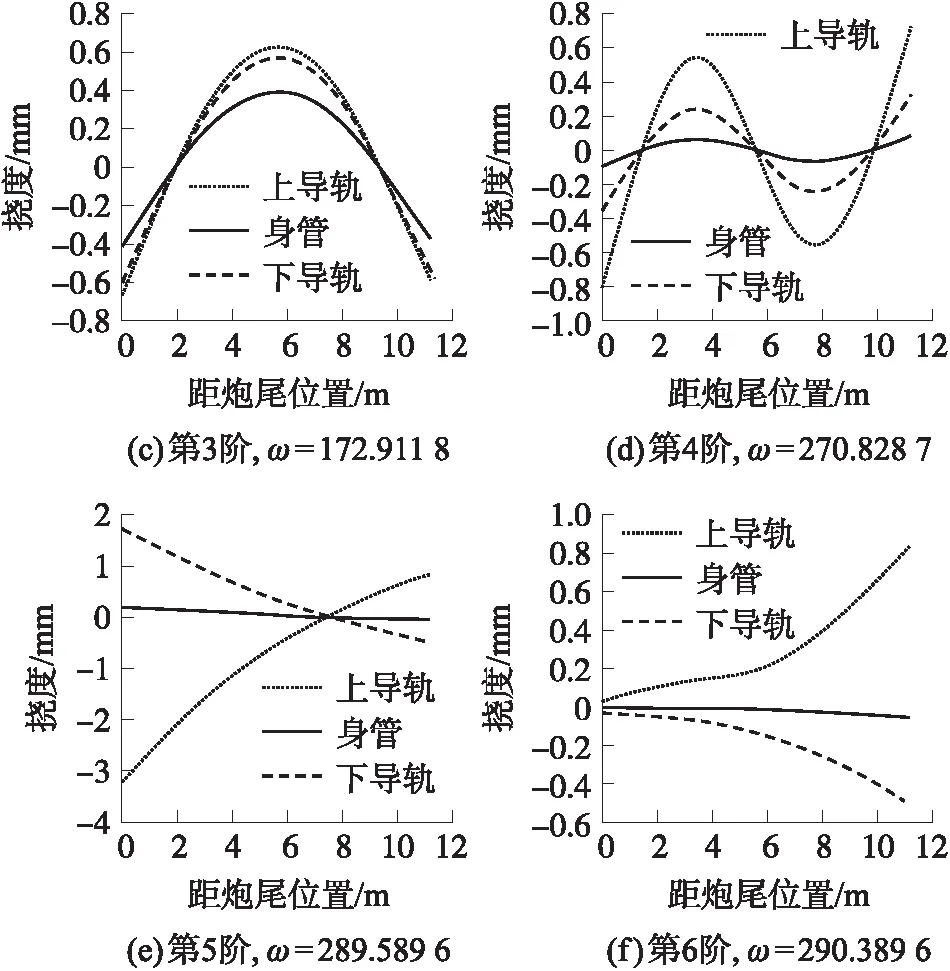
图7 导轨身管系统前六阶模态振型Fig.7 The first six modes of guide rail tube system

3.2 导轨身管系统静位移

导轨身管三梁系统在重力作用下的静位移计算结果如图8所示。由图8可以看出,上导轨、身管和下导轨静位移趋势一致,均为炮尾处的静位移达到最大值,炮口处静位移略微上翘,且由于实际结构材料与装配过程中的误差,上下导轨与身管间的接触刚度存在差异,导致上下导轨在重力作用下的静位移略有不同。MSTMM计算结果与有限元比较最大相对误差为0.84%。

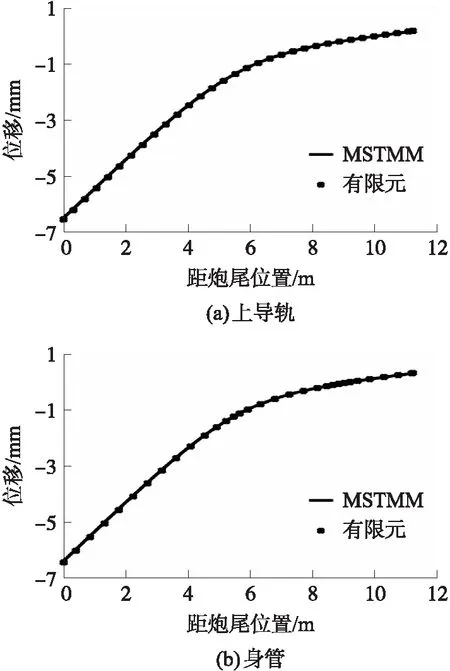
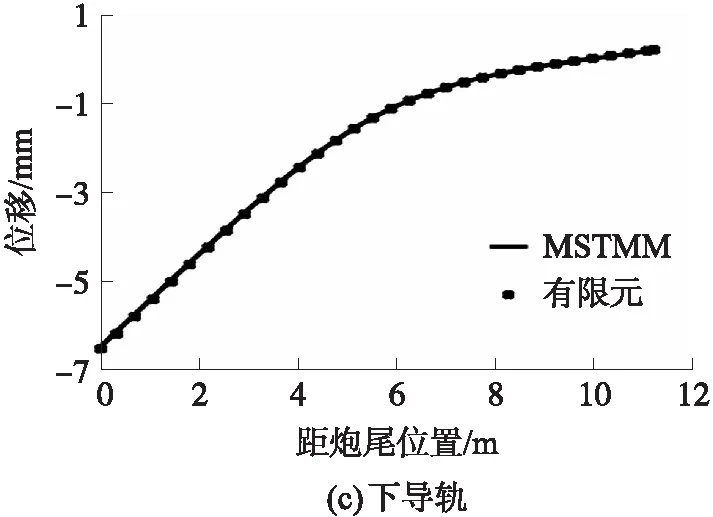
图8 导轨身管系统重力作用下的静位移Fig.8 Static displacement of guide rail barrel system under gravity

3.3 系统所受电磁载荷

当电枢在炮口位置时,系统导轨所受电磁力分布计算结果如图9所示。由图可知,导轨间的电磁载荷在靠近炮尾的一段距离处迅速增大,然后基本保持不变,最后在靠近电枢的一段距离处迅速减小,且增大和减小的区域成对称分布;电枢对导轨的电磁载荷在远离电枢处很小,接近电枢位置时迅速增大。考虑到电磁载荷在导轨中间位置变化很小,只在炮尾和电枢附近有显著变化,因此,可将导轨受到的电磁载荷简化为均布载荷q和集中力F的组合。

图9 导轨所受电磁力作用系数Fig.9 Distribution of electromagnetic force on guide rail

3.4 导轨身管系统动态响应

导轨身管系统在重力及时变电磁力作用下的系统动态响应计算结果如图10和图11所示。由图可以看出,在电流上升初期,电磁力与重力相比对系统影响较小,系统横向位移均在炮尾处达到最大值,当电流处于峰值平台期间,上下导轨受枢轨间电磁力作用,动态响应幅值逐渐达到峰值,同一时刻,上下导轨动态响应幅值并不相同,系统横向位移最大值出现在系统两端(炮口或炮尾);身管在通电过程中波动范围变化不大,横向位移幅值小于上下导轨横向位移幅值,受地面固定位置弹性支撑作用影响,身管炮尾处横向位移变化量大于炮口位置处。

图10 导轨身管系统动态响应Fig.10 Dynamic response of guide rail barrel system

图11 导轨身管系统炮口处位移-时间曲线Fig.11 Displacement-time curve at the muzzle of guide rail barrel system

在炮口位置处,上下导轨位移-时间曲线与身管位移-时间曲线的变化趋势保持一致,由于弹性支撑参数等非对称性因素的影响,上导轨炮口点变形量更大;在系统初始阶段,由于流经轨道的电流较小,上下导轨及身管炮口点均以静变形位置为平衡位置上下波动,随着电流到达峰值平台,导轨间的电磁斥力逐渐变大,在身管结构支撑的共同作用下,上下导轨炮口处间距在“扩张-收缩”的过程中反复震荡,当轨道电流处于指数衰减阶段时,导轨间的电磁斥力迅速减小,上下导轨及身管炮口点在静变形位置附近上下振动。

4 结束语

本文以电磁轨道炮导轨身管发射装置为研究对象,对导轨身管系统的动力学模型、振动特性、动态响应等问题进行了探究,利用MSTMM建立导轨身管系统三梁动力学模型,以电磁场计算出的电磁力为激励源,利用模态叠加法求解导轨身管系统在重力及时变电磁力作用下的动态响应,探究了上下导轨非对称性对系统静变形及动态响应的影响,并通过有限元法验证了MSTMM的正确性和快速性。下一步将讨论考虑一体化发射弹丸膛内运动过程和时变电磁载荷的弹轨耦合发射动力学模型。